Vloeistofviscositeit bij lage temperaturen: invloed op de reactietijd van de cilinder

Wanneer uw pneumatische systemen op koude ochtenden traag opstarten of tijdens winterwerkzaamheden niet aan de cyclustijdvereisten voldoen, ondervindt u de vaak over het hoofd geziene effecten van temperatuurafhankelijke luchtviscositeit. Deze onzichtbare prestatiekiller kan de responstijden van cilinders bij extreme kou met 50-80% verlengen, wat leidt tot productievertragingen en timingproblemen die operators toeschrijven aan “apparatuurproblemen” in plaats van aan fundamentele vloeistofdynamica. ❄️

De viscositeit van lucht neemt bij lage temperaturen aanzienlijk toe volgens de wet van Sutherland, waardoor de stromingsweerstand door kleppen, fittingen en cilinderpoorten toeneemt. Dit verlengt de reactietijd van de cilinder doordat de stroomsnelheid afneemt en de drukopbouwperiode die nodig is om de beweging in gang te zetten, langer duurt.

Vorige maand werkte ik samen met Robert, een fabrieksmanager bij een koelopslagfaciliteit in Minnesota, waar het geautomatiseerde verpakkingssysteem tijdens de wintermaanden 40% langere cyclustijden kende, wat een bottleneck veroorzaakte die de doorvoer met 15.000 eenheden per dag verminderde.

Inhoudsopgave

• Hoe beïnvloedt temperatuur de viscositeit van lucht in pneumatische systemen?
• Wat is het verband tussen viscositeit en stromingsweerstand?
• Hoe kunt u door temperatuur veroorzaakte vertragingen in reacties meten en voorspellen?
• Welke oplossingen kunnen prestatieverlies bij lage temperaturen minimaliseren?

Hoe beïnvloedt temperatuur de viscositeit van lucht in pneumatische systemen?

Inzicht in de relatie tussen temperatuur en viscositeit is van fundamenteel belang voor het voorspellen van prestaties bij koud weer. 🌡️

De viscositeit van lucht neemt toe naarmate de temperatuur daalt, volgens de wet van Sutherland: \( \mu = \mu_{0} \times (T/T_{0})^{1,5} \times \frac{T_{0} + S}{T + S} \), waarbij de viscositeit met 35% kan toenemen wanneer de temperatuur daalt van +20^\circ\text{C} naar -20^\circ\text{C}, wat een aanzienlijke invloed heeft op de stromingseigenschappen door pneumatische componenten.

De wet van Sutherland voor luchtviscositeit

De relatie tussen temperatuur en luchtviscositeit is als volgt:
$$
\mu = \mu_{0} \times \left( \frac{T}{T_{0}} \right)^{1,5} \times \frac{T_{0} + S}{T + S}
$$

Waar:

• \( \mu \) = Dynamische viscositeit bij temperatuur ( T )
• \( \mu_{0} \) = Referentieviscositeit (1,716 × 10⁻⁵ Pa·s bij 273 K)
• \( T \) = Absolute temperatuur (K)
• \( T_{0} \) = Referentietemperatuur (273 K)
• \( S \) = Sutherland-constante¹ (111K voor lucht)

Viscositeit-temperatuurgegevens

Temperatuur	Dynamische viscositeit	Kinematische viscositeit	Relatieve verandering
+40 °C	1,91 × 10⁻⁵ Pa·s	1,69 × 10⁻⁵ m²/s	+11%
+20°C	1,82 × 10⁻⁵ Pa·s	1,51 × 10⁻⁵ m²/s	Referentie
0 °C	1,72 × 10⁻⁵ Pa·s	1,33 × 10⁻⁵ m²/s	-5%
-20°C	1,63 × 10⁻⁵ Pa·s	1,17 × 10⁻⁵ m²/s	-13%
-40°C	1,54 × 10⁻⁵ Pa·s	1,03 × 10⁻⁵ m²/s	-22%

Fysieke mechanismen

Moleculair gedrag:

• Kinetische theorie²Lagere temperaturen verminderen moleculaire beweging.
• Intermoleculaire krachten: Sterkere aantrekkingskracht bij lagere temperaturen
• Momentum transfer: Verminderde moleculaire impulsuitwisseling
• Frequentie van botsingen: Temperatuur beïnvloedt de snelheid van moleculaire botsingen

Praktische implicaties:

• Stromingsweerstand: Een hogere viscositeit verhoogt de drukval.
• Reynoldsgetal³: Lower Re beïnvloedt overgangen in stromingsregimes
• Warmteoverdracht: Viscositeitsveranderingen beïnvloeden convectieve warmteoverdracht
• Samendrukbaarheid: Temperatuur beïnvloedt de gasdichtheid en samendrukbaarheid.

Effecten op systeemniveau

Component-specifieke effecten:

• Kleppen: Langere omschakeltijden, hogere drukdalingen
• Filters: Verminderde doorstroomcapaciteit, hogere drukverschillen
• Regelaars: Langzamere respons, mogelijk jagen
• Cilinders: Langere vultijden, verminderde acceleratie

Veranderingen in het stromingsregime:

• Laminaire stroming⁴: Viscositeit heeft een directe invloed op de drukval (ΔP ∝ μ)
• Turbulente stroming: Minder gevoelig maar nog steeds beïnvloed (ΔP ∝ μ^0,25)
• OvergangsgebiedVeranderingen in het Reynoldsgetal beïnvloeden de stabiliteit van de stroming.

Casestudy: Robert's koelopslagfaciliteit

De fabriek van Robert in Minnesota ondervond ernstige gevolgen van de temperatuur:

• Bedrijfstemperatuurbereik: -25 °C tot +5 °C
• Viscositeitsvariatie: 40%-toename bij koudste omstandigheden
• Gemeten toename van de responstijd: 65% bij -25 °C versus +20 °C
• Reductie van het debiet: 35% door systeembeperkingen
• Productie-impact: 15.000 eenheden/dag aan doorvoer verlies

Wat is het verband tussen viscositeit en stromingsweerstand?

De stromingsweerstand neemt rechtstreeks toe met de viscositeit, wat een cascade-effect veroorzaakt in pneumatische systemen. 💨

De stromingsweerstand in pneumatische systemen neemt evenredig toe met de viscositeit in laminaire stromingsomstandigheden \( \Delta P = \frac{32 \mu L Q}{\pi D^{4}} \) en met de 0,25 macht van de viscositeit in turbulente stroming, wat leidt tot een exponentiële toename van de reactietijd van de cilinder naarmate meerdere beperkingen zich in het hele systeem opstapelen.

Fundamentele stromingsvergelijkingen

Laminaire stroming (Re < 2300):

$$
\Delta P = \frac{32 \mu L Q}{\pi D^{4}}
$$

Waar:

• \( \Delta P \) = Drukval
• \( \mu \) = Dynamische viscositeit
• \( L \) = Lengte
• \( Q \) = Volumetrisch debiet
• \( D \) = Diameter

Turbulente stroming (Re > 4000):

$$
\Delta P = f \times \left( \frac{L}{D} \right) \times \frac{\rho V^{2}}{2}
$$

Waarbij de wrijvingsfactor \( f \) evenredig is aan \( \mu^{0,25} \).

Temperatuurafhankelijkheid van het Reynoldsgetal

$$
Re = \frac{\rho V D}{\mu}
$$

Naarmate de temperatuur daalt:

• De dichtheid (\( \rho \)) neemt toe
• De viscositeit (\( \mu \)) neemt toe.
• Netto-effect: het Reynoldsgetal neemt doorgaans af.

Stroomweerstand in systeemcomponenten

Component	Type stroom	Viscositeitsgevoeligheid	Invloed van temperatuur
Kleine openingen	Laminair	Hoog (∝ μ)	35%-toename bij -20 °C
Kleppoorten	Overgang	Gemiddeld (∝ μ^0,5)	18%-toename bij -20 °C
Grote passages	Turbulent	Laag (∝ μ^0,25)	8%-toename bij -20 °C
Filters	Gemengd	Hoog	25-40% stijging bij -20 °C

Cumulatieve systeemeffecten

Serieweerstand:

Meerdere beperkingen toevoegen:
$$
R_{\text{totaal}} = R_{1} + R_{2} + R_{3} + \cdots + R_{n}
$$

De weerstand van elk onderdeel neemt toe met de viscositeit, waardoor cumulatieve vertragingen ontstaan.

Parallelle weerstand:

$$
\frac{1}{R_{\text{totaal}}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \cdots + \frac{1}{R_{n}}
$$

Zelfs parallelle paden worden beïnvloed wanneer iedereen meer weerstand ondervindt.

Tijdconstante analyse

RC-tijdconstante:

$$
\tau = RC = (\text{Weerstand} \times \text{Capaciteit})
$$

Waar:

• \( R \) neemt toe met viscositeit
• \( C \) (systeemcapaciteit) blijft constant
• Resultaat: Langere tijdconstanten, tragere respons

Eerste reactie:

$$
P(t) = P_{\text{eind}} \times \left( 1 – e^{-t/\tau} \right)
$$

Een hogere viscositeit verhoogt \( \tau \), waardoor de drukopbouwtijd wordt verlengd.

Dynamische respons modelleren

Vultijd cilinder:

$$
t_{\text{vulling}} = \frac{V \times \Delta P}{Q_{\text{gem}}}
$$

Waar \( Q_{\text{avg}} \) afneemt bij toenemende viscositeit.

Versnellingsfase:

$$
t_{\text{accel}} = \frac{m \times v_{\text{max}}}{F_{\text{avg}}}
$$

Waar \( F_{\text{avg}} \) afneemt als gevolg van een langzamere drukopbouw.

Meting en validatie

Resultaten van de doorstroomtest:

In het systeem van Robert bij verschillende temperaturen:

• +5°C: 45 SCFM via hoofdklep
• -10 °C: 38 SCFM via hoofdklep (16%-reductie)
• -25°C: 29 SCFM via hoofdklep (36%-reductie)

Metingen van de responstijd:

• +5°C: gemiddelde cilinderrespons van 180 ms
• -10 °C: 235 ms gemiddelde cilinderrespons (+31%)
• -25°C: gemiddelde cilinderrespons van 295 ms (+64%)

Hoe kunt u door temperatuur veroorzaakte vertragingen in reacties meten en voorspellen?

Nauwkeurige meting en voorspelling van temperatuureffecten maakt proactieve systeemoptimalisatie mogelijk. 📊

Meet temperatuurgeïnduceerde vertragingen met behulp van snelle data-acquisitie om de timing tussen klepbediening en cilinderbeweging over verschillende temperatuurbereiken te registreren. Ontwikkel vervolgens voorspellende modellen met behulp van viscositeit-stromingsrelaties en thermische coëfficiënten om de prestaties bij verschillende bedrijfstemperaturen te voorspellen.

Vereisten voor het instellen van metingen

Essentiële instrumentatie:

• Temperatuursensoren: RTD's⁵ of thermokoppels (nauwkeurigheid ±0,5 °C)
• Drukomzetters: Snelle respons (<1 ms), hoge nauwkeurigheid
• PositiesensorenLineaire encoders of naderingsschakelaars
• Debietmeters: Massastroom- of volumestroommeting
• Gegevensverwerving: Snelle bemonstering (≥1 kHz)

Meetpunten:

• Omgevingstemperatuur: Omgevingsomstandigheden
• Luchttoevoertemperatuur: Temperatuur van perslucht
• Temperaturen van componenten: Kleppen, cilinders, filters
• Systeemdrukken: Toevoer-, werk- en afvoerdrukken
• Tijdmetingen: Klepsignaal voor het starten van de beweging

Testmethodologie

Testen bij gecontroleerde temperatuur:

1. Milieukamer: Regel de omgevingstemperatuur
2. Thermisch evenwicht: Laat 30-60 minuten stabiliseren.
3. Basisinstelling: Recordprestaties bij referentietemperatuur
4. Temperatuursweep: Test over het gehele werkingsbereik
5. Herhaalbaarheidscontrole: Meerdere cycli bij elke temperatuur

Protocol voor veldtesten:

1. Seizoensgebonden monitoring: Langdurige gegevensverzameling
2. Dagelijkse temperatuurcycli: Prestatieverschillen bijhouden
3. Vergelijkende analyse: Vergelijkbare systemen in verschillende omgevingen
4. Belastingsvariatie: Test onder verschillende bedrijfsomstandigheden

Voorspellende modelleringsbenaderingen

Empirische correlatie:

$$
t_{\text{respons}}
= t_{\text{ref}} \times \left( \frac{\mu}{\mu_{\text{ref}}} \right)^{\alpha}
\times \left( \frac{T_{\text{ref}}}{T} \right)^{\beta}
$$

Waarbij \( \alpha \) en \( \beta \) systeemspecifieke constanten zijn die experimenteel zijn bepaald.

Op fysica gebaseerd model:

$$
t_{\text{respons}} = t_{\text{klep}} + t_{\text{vulling}} + t_{\text{versnelling}}
$$

Waarbij elke component wordt berekend aan de hand van temperatuurafhankelijke eigenschappen.

Technieken voor modelvalidatie

Validatiemethode	Nauwkeurigheid	Toepassing	Complexiteit
Laboratoriumtests	±5%	Nieuwe ontwerpen	Hoog
Veldcorrelatie	±10%	Bestaande systemen	Medium
CFD-simulatie	±15%	Ontwerpoptimalisatie	Zeer hoog
Empirische schaalvergroting	±20%	Snelle schattingen	Laag

Gegevensanalyse en correlatie

Statistische analyse:

• RegressieanalyseOntwikkel correlaties tussen temperatuur en reactie.
• Betrouwbaarheidsintervallen: Kwantificeer de onzekerheid van voorspellingen
• Detectie van uitschieters: Identificeer afwijkende gegevenspunten
• Gevoeligheidsanalyse: Bepaal kritische temperatuurbereiken

Prestatiekaart:

• Reactietijd versus temperatuur: Primaire relatie
• Debiet versus temperatuur: Ondersteuning van correlatie
• Efficiëntie versus temperatuur: Energie-effectbeoordeling
• Betrouwbaarheid versus temperatuur: Analyse van het percentage mislukkingen

Voorspellende modelontwikkeling

Voor het koelopslagsysteem van Robert:

Responstijdmodel:
$$
t_{\text{respons}}(T)
= 180 \times \left( \frac{T_{\text{ref}}}{T} \right)^{0,65}
\times \left( \frac{\mu(T)} {\mu_{\text{ref}}} \right)^{0,85}
$$

Validatieresultaten:

• Correlatiecoëfficiënt: R² = 0,94
• Gemiddelde fout: ±8%
• Temperatuurbereik: -25 °C tot +5 °C
• Voorspellingsnauwkeurigheid: ±15 ms bij extreme temperaturen

Debietmodel:

$$
Q(T)
= Q_{\text{ref}} \times \left( \frac{T}{T_{\text{ref}}} \right)^{0,5}
\times \left( \frac{\mu_{\text{ref}}}{\mu(T)} \right)^{0,75}
$$

Modelprestaties:

• Nauwkeurigheid van de stroomberekening: ±12%
• Correlatie drukval: R² = 0,91
• Systeemoptimalisatie: 25% verbetering van de prestaties bij koud weer

Vroegtijdige waarschuwingssystemen

Temperatuurgestuurde waarschuwingen:

• Prestatievermindering: >20% responstijdtoename
• Kritische temperatuur: Onder -15 °C voor dit systeem
• Trendanalyse: Mate van invloed van temperatuurveranderingen
• Voorspellend onderhoud: Schema gebaseerd op blootstelling aan temperatuur

Welke oplossingen kunnen prestatieverlies bij lage temperaturen minimaliseren?

Om de effecten van koude temperaturen te beperken, zijn uitgebreide maatregelen nodig op het gebied van warmtebeheer, componentkeuze en systeemontwerp. 🛠️

Minimaliseer prestatieverlies bij lage temperaturen door middel van systeemverwarming (verwarmde behuizingen, traceverwarming), componentoptimalisatie (grotere doorstroomkanalen, lage-temperatuurkleppen), vloeistofconditionering (luchtdrogers, temperatuurregeling) en aanpassing van het regelsysteem (temperatuurcompensatie, verlengde timing).

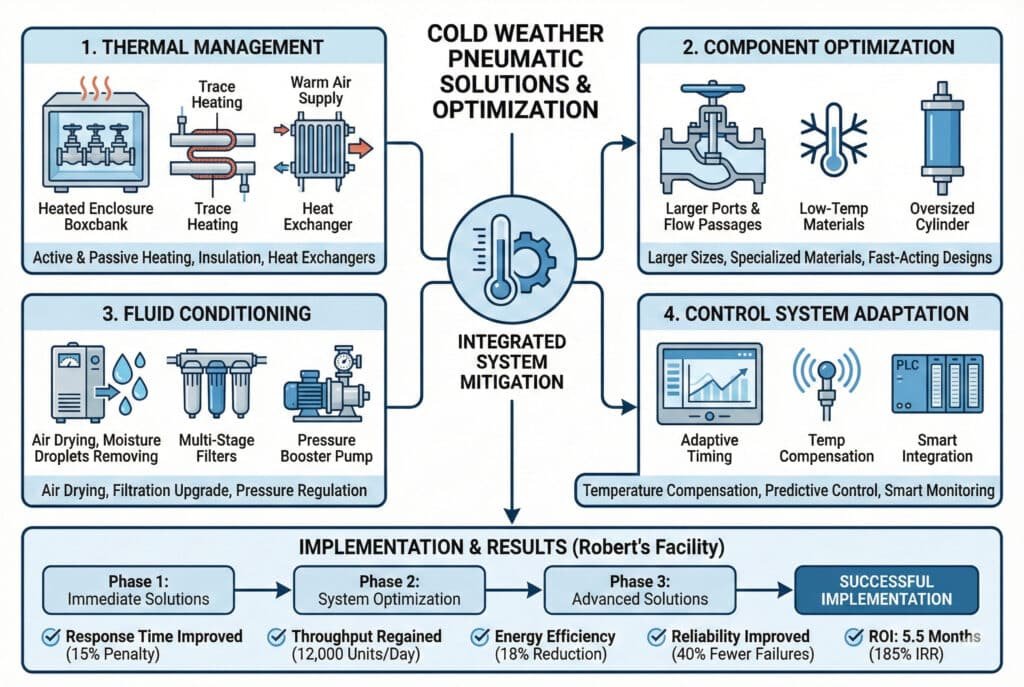
Oplossingen voor thermisch beheer

Actieve verwarmingssystemen:

• Verwarmde behuizingen: Houd de temperatuur van componenten boven kritieke drempels.
• Sporenverwarming: Elektrische verwarmingskabels op pneumatische leidingen
• Warmtewisselaars: Warme inkomende perslucht
• Thermische isolatieVerminder warmteverlies van systeemcomponenten

Passief thermisch beheer:

• Thermische massaGrote componenten houden de temperatuur op peil.
• IsolatieVoorkom warmteverlies naar de omgeving.
• Thermische bruggen: Leid warmte af van warme gebieden
• Verwarming op zonne-energie: Gebruik beschikbare zonne-energie

Optimalisatie van onderdelen

Klepselectie:

• Grotere poortmaten: Verminder viscositeitsgevoelige drukdalingen
• Materialen voor lage temperaturen: Behoud flexibiliteit bij lage temperaturen
• Snelwerkende ontwerpen: Minimaliseer de tijdverliezen bij het wisselen
• Geïntegreerde verwarming: Ingebouwde temperatuurcompensatie

Wijzigingen in het systeemontwerp:

• Te grote onderdelen: Compenseer voor verminderde doorstroomcapaciteit
• Parallelle stromingspaden: Beperkingen voor individuele paden verminderen
• Kortere lijnlengtes: Minimaliseer cumulatieve drukverliezen
• Geoptimaliseerde routeplanning: Bescherm tegen blootstelling aan kou

Vloeistofconditionering

Oplossing	Temperatuurvoordeel	Implementatiekosten	Doeltreffendheid
Luchtverwarming	15-25 °C stijging	Hoog	Zeer hoog
Vochtverwijdering	Voorkomt bevriezing	Medium	Hoog
Filtratie-upgrade	Houdt de doorstroming in stand	Laag	Medium
Drukverhoging	Overwint beperkingen	Medium	Hoog

Geavanceerde regelstrategieën

Temperatuurcompensatie:

• Adaptieve timing: Pas de cyclustijden aan op basis van de temperatuur.
• Drukprofilering: Verhoog de toevoerdruk bij lage temperaturen
• Stroomcompensatie: Kleptiming aanpassen voor temperatuureffecten
• Voorspellende controle: Anticipeer op vertragingen als gevolg van temperatuur

Slimme systeemintegratie:

• Temperatuurbewaking: Continue temperatuurregistratie van het systeem
• Automatische aanpassing: Real-time compensatie voor temperatuureffecten
• Prestatieoptimalisatie: Dynamische systeemafstemming
• Onderhoudsplanning: Op temperatuur gebaseerde onderhoudsintervallen

Bepto's oplossingen voor koud weer

Bij Bepto Pneumatics hebben we gespecialiseerde oplossingen ontwikkeld voor toepassingen bij lage temperaturen:

Ontwerpinnovaties:

• Cilinders voor koud weer: Geoptimaliseerd voor gebruik bij lage temperaturen
• Geïntegreerde verwarming: Ingebouwd temperatuurbeheer
• Afdichtingen voor lage temperaturen: Flexibiliteit en afdichting behouden
• Thermische bewaking: Real-time temperatuurfeedback

Prestatieverbeteringen:

• Te grote poorten: 40% groter dan standaard voor viscositeitscompensatie
• Thermische isolatie: Geïntegreerde isolatiesystemen
• Verwarmde verdeelstukken: Zorg voor optimale componenttemperaturen
• Slimme bedieningselementen: Temperatuuraanpassende regelalgoritmen

Implementatiestrategie voor de faciliteit van Robert

Fase 1: Onmiddellijke oplossingen (week 1-2)

• Installatie van isolatie: Wikkel kritieke pneumatische componenten in
• Verwarmde behuizingen: Installeer rond kleppenkoppelingen
• Verwarming van toevoerluchtWarmtewisselaar op persluchttoevoer
• Controleaanpassingen: Verleng de cyclustijden tijdens koude periodes

Fase 2: Systeemoptimalisatie (maand 1-2)

• Upgrades voor onderdelen: Vervang door kleppen die zijn geoptimaliseerd voor koud weer
• Wijzigingen in de lijn: Pneumatische leidingen met grotere diameter
• Verbeteringen in filtratie: Filters met hoge doorstroming en lage weerstand
• Monitoringsysteem: Temperatuur en prestaties bijhouden

Fase 3: Geavanceerde oplossingen (maand 3-6)

• Slimme bedieningselementen: Temperatuurgecompenseerd regelsysteem
• Voorspellende algoritmen: Anticiperen op en compenseren voor temperatuureffecten
• Energieoptimalisatie: Verwarmingskosten in evenwicht brengen met prestatieverbeteringen
• Optimalisatie van onderhoud: Op temperatuur gebaseerde serviceplanning

Resultaten en prestatieverbetering

De implementatieresultaten van Robert:

• Verbetering van de responstijd: Vermindering van de straf bij koud weer van 65% naar 15%
• Doorvoerherstel: 12.000 van de 15.000 verloren eenheden/dag teruggewonnen
• Energie-efficiëntie: 18% vermindering van het persluchtverbruik
• Betrouwbaarheidsverbetering: 40% vermindering van storingen bij koud weer

Kosten-batenanalyse

Implementatiekosten:

• Verwarmingssystemen: $45,000
• Upgrades voor onderdelen: $28,000
• Besturingssysteem: $15,000
• Installatie/inbedrijfstelling: $12,000
• Totale investering: $100,000

Jaarlijkse voordelen:

• Herstel van de productie: $180.000 (doorvoerverbetering)
• Energiebesparing: $25.000 (efficiëntiewinst)
• Vermindering van onderhoud: $15.000 (minder storingen bij koud weer)
• Totaal jaarlijks voordeel: $220,000

ROI-analyse:

• Terugverdientijd: 5,5 maanden
• 10-jaars NCW: $1,65 miljoen
• Interne rentevoet: 185%

Onderhoud en controle

Preventief onderhoud:

• Seizoensvoorbereiding: Systeemoptimalisatie vóór de winter
• Temperatuurbewaking: Voortdurend bijhouden van prestaties
• Inspectie van onderdelen: Regelmatige controle van verwarmingssystemen
• PrestatievalidatieControleer de effectiviteit van de temperatuurcompensatie.

Optimalisatie op lange termijn:

• Gegevensanalyse: Continue verbetering op basis van prestatiegegevens
• Systeemupgrades: Evoluerende technologie-integratie
• Trainingsprogramma's: Opleiding van operators over temperatuureffecten
• Beste praktijkenDocumentatie en kennisdeling

De sleutel tot succesvol gebruik bij koud weer ligt in het besef dat temperatuureffecten voorspelbaar en beheersbaar zijn door middel van de juiste techniek en systeemontwerp. 🎯

Veelgestelde vragen over vloeistofviscositeit en effecten van koude temperaturen

1. Lees meer over de specifieke constante die is afgeleid van intermoleculaire aantrekkingskracht en wordt gebruikt om de viscositeit van gas te berekenen. ↩

2. Ontdek de theorie die de macroscopische eigenschappen van gas verklaart op basis van moleculaire beweging. ↩

3. Lees meer over de dimensieloze grootheid die vloeistofstromingspatronen voorspelt. ↩

4. Begrijp het soepele, parallelle stromingsregime dat bij lage snelheden overheerst. ↩

5. Bekijk het werkingsprincipe van weerstandstemperatuursensoren voor nauwkeurige thermische metingen. ↩