Lepkość płynów w niskich temperaturach: wpływ na czas reakcji cylindra

Kiedy Twoje systemy pneumatyczne zaczynają działać wolno w chłodne poranki lub nie spełniają wymagań dotyczących czasu cyklu podczas pracy w zimie, doświadczasz często pomijanych skutków zależnej od temperatury lepkości powietrza. Ten niewidoczny czynnik obniżający wydajność może wydłużyć czas reakcji cylindra o 50-80% w ekstremalnie niskich temperaturach, powodując opóźnienia w produkcji i problemy z synchronizacją, które operatorzy przypisują “problemom ze sprzętem”, a nie podstawowej dynamice płynów. ❄️

Lepkość powietrza znacznie wzrasta w niskich temperaturach zgodnie z prawem Sutherlanda, powodując większy opór przepływu przez zawory, złączki i otwory cylindrów, co bezpośrednio wydłuża czas reakcji cylindra poprzez zmniejszenie natężenia przepływu i wydłużenie okresów wzrostu ciśnienia wymaganych do zainicjowania ruchu.

W zeszłym miesiącu współpracowałem z Robertem, kierownikiem zakładu w chłodni w Minnesocie, którego zautomatyzowany system pakowania doświadczał wydłużenia cyklu o 40% w miesiącach zimowych, powodując wąskie gardło, które zmniejszało przepustowość o 15 000 jednostek dziennie.

Spis treści

• W jaki sposób temperatura wpływa na lepkość powietrza w układach pneumatycznych?
• Jaki jest związek między lepkością a oporem przepływu?
• Jak można mierzyć i przewidywać opóźnienia reakcji spowodowane temperaturą?
• Jakie rozwiązania mogą zminimalizować spadek wydajności w niskich temperaturach?

W jaki sposób temperatura wpływa na lepkość powietrza w układach pneumatycznych?

Zrozumienie zależności między temperaturą a lepkością ma fundamentalne znaczenie dla przewidywania właściwości w niskich temperaturach. 🌡️

Lepkość powietrza wzrasta wraz ze spadkiem temperatury zgodnie z prawem Sutherlanda: \( \mu = \mu_{0} \times (T/T_{0})^{1,5} \times \frac{T_{0} + S}{T + S} \), gdzie lepkość może wzrosnąć o 35%, gdy temperatura spadnie z +20^\circ\text{C} do -20^\circ\text{C}, co znacząco wpływa na charakterystykę przepływu przez elementy pneumatyczne.

Prawo Sutherlanda dotyczące lepkości powietrza

Zależność między temperaturą a lepkością powietrza jest następująca:
$$
\mu = \mu_{0} \times \left( \frac{T}{T_{0}} \right)^{1,5} \times \frac{T_{0} + S}{T + S}
$$

Gdzie:

• \( \mu \) = lepkość dynamiczna w temperaturze ( T )
• \( \mu_{0} \) = lepkość odniesienia (1,716 × 10⁻⁵ Pa·s w temperaturze 273 K)
• \( T \) = Temperatura bezwzględna (K)
• \( T_{0} \) = Temperatura odniesienia (273 K)
• \( S \) = Stała Sutherlanda¹ (111 tys. za powietrze)

Dane dotyczące lepkości i temperatury

Temperatura	Lepkość dynamiczna	Lepkość kinematyczna	Zmiana względna
+40°C	1,91 × 10⁻⁵ Pa·s	1,69 × 10⁻⁵ m²/s	+11%
+20°C	1,82 × 10⁻⁵ Pa·s	1,51 × 10⁻⁵ m²/s	Odniesienie
0°C	1,72 × 10⁻⁵ Pa·s	1,33 × 10⁻⁵ m²/s	-5%
-20°C	1,63 × 10⁻⁵ Pa·s	1,17 × 10⁻⁵ m²/s	-13%
-40°C	1,54 × 10⁻⁵ Pa·s	1,03 × 10⁻⁵ m²/s	-22%

Mechanizmy fizyczne

Zachowanie molekularne:

• Teoria kinetyczna²: Niższe temperatury zmniejszają ruch cząsteczek.
• Siły międzycząsteczkowe: Silniejsza przyciąganie w niższych temperaturach
• Transfer pędu: Zmniejszona wymiana pędu molekularnego
• Częstotliwość kolizji: Temperatura wpływa na częstotliwość zderzeń cząsteczek.

Praktyczne implikacje:

• Opór przepływu: Wyższa lepkość powoduje wzrost spadku ciśnienia.
• Liczba Reynoldsa³: Dolna Re wpływa na zmiany reżimu przepływu
• Transfer ciepła: Zmiany lepkości wpływają na konwekcyjne przenoszenie ciepła.
• Ściśliwość: Temperatura wpływa na gęstość i ściśliwość gazu.

Efekty na poziomie systemu

Wpływ poszczególnych elementów:

• Zawory: Wydłużony czas przełączania, większe spadki ciśnienia
• Filtry: Zmniejszona przepustowość, wyższa różnica ciśnień
• Regulatory: Wolniejsza reakcja, potencjalne poszukiwania
• Cylindry: Dłuższy czas napełniania, zmniejszone przyspieszenie

Zmiany reżimu przepływu:

• Przepływ laminarny⁴: Lepkość ma bezpośredni wpływ na spadek ciśnienia (ΔP ∝ μ)
• Przepływ burzliwy: Mniej wrażliwe, ale nadal podatne (ΔP ∝ μ^0,25)
• Region przejściowy: Zmiany liczby Reynoldsa wpływają na stabilność przepływu.

Studium przypadku: Chłodnia Roberta

Zakład Roberta w stanie Minnesota doświadczył poważnych skutków temperatury:

• Zakres temperatur pracyod -25°C do +5°C
• Zmienność lepkości: Wzrost 40% w najzimniejszych warunkach
• Zmierzony wzrost czasu reakcji: 65% w temperaturze -25°C w porównaniu z +20°C
• Redukcja natężenia przepływu: 35% z powodu ograniczeń systemowych
• Wpływ na produkcję: 15 000 jednostek/dzień utraty wydajności

Jaki jest związek między lepkością a oporem przepływu?

Opór przepływu wzrasta bezpośrednio wraz z lepkością, powodując efekt kaskadowy w całym układzie pneumatycznym. 💨

Opór przepływu w układach pneumatycznych wzrasta proporcjonalnie do lepkości w warunkach przepływu laminarnego \( \Delta P = \frac{32 \mu L Q}{\pi D^{4}} \) oraz do potęgi 0,25 lepkości w przepływie turbulentnym, powodując wykładniczy wzrost czasu reakcji cylindra w miarę narastania wielu ograniczeń w całym układzie.

Podstawowe równania przepływu

Przepływ laminarny (Re < 2300):

$$
\Delta P = \frac{32 \mu L Q}{\pi D^{4}}
$$

Gdzie:

• \( \Delta P \) = spadek ciśnienia
• \( \mu \) = lepkość dynamiczna
• \( L \) = długość
• \( Q \) = Przepływ objętościowy
• \( D \) = Średnica

Przepływ burzliwy (Re > 4000):

$$
\Delta P = f \times \left( \frac{L}{D} \right) \times \frac{\rho V^{2}}{2}
$$

Gdzie współczynnik tarcia \( f \) jest proporcjonalny do \( \mu^{0,25} \).

Zależność temperatury od liczby Reynoldsa

$$
Re = \frac{\rho V D}{\mu}
$$

Wraz ze spadkiem temperatury:

• Gęstość (\( \rho \)) wzrasta
• Lepkość (\( \mu \)) wzrasta
• Efekt netto: liczba Reynoldsa zazwyczaj maleje.

Opór przepływu w komponentach systemu

Komponent	Typ przepływu	Wrażliwość na lepkość	Wpływ temperatury
Małe otwory	Laminar	Wysoka (∝ μ)	Wzrost 35% w temperaturze -20°C
Porty zaworów	Przejściowy	Średni (∝ μ^0,5)	Wzrost 18% w temperaturze -20°C
Duże przejścia	Turbulentny	Niski (∝ μ^0,25)	Wzrost 8% w temperaturze -20°C
Filtry	Mieszane	Wysoki	Wzrost 25-40% w temperaturze -20°C

Skumulowane skutki systemu

Rezystancja szeregowa:

Dodaj wiele ograniczeń:
$$
R_{\text{całkowita}} = R_{1} + R_{2} + R_{3} + \cdots + R_{n}
$$

Opór każdego elementu wzrasta wraz z lepkością, powodując kumulujące się opóźnienia.

Rezystancja równoległa:

$$
\frac{1}{R_{\text{total}}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \cdots + \frac{1}{R_{n}}
$$

Nawet ścieżki równoległe są dotknięte tym zjawiskiem, gdy wszystkie napotykają zwiększony opór.

Analiza stałej czasowej

Stała czasowa RC:

$$
\tau = RC = (\text{Rezystancja} \times \text{Pojemność})
$$

Gdzie:

• \( R \) rośnie wraz z lepkością
• \( C \) (pojemność systemu) pozostaje stała
• Wynik: Dłuższe stałe czasowe, wolniejsza reakcja

Odpowiedź pierwszego rzędu:

$$
P(t) = P_{\text{końcowe}} \times \left( 1 – e^{-t/\tau} \right)
$$

Wyższa lepkość zwiększa \( \tau \), wydłużając czas narastania ciśnienia.

Modelowanie odpowiedzi dynamicznej

Czas napełniania butli:

$$
t_{\text{wypełnienie}} = \frac{V \times \Delta P}{Q_{\text{średnia}}}
$$

Gdzie \( Q_{\text{avg}} \) maleje wraz ze wzrostem lepkości.

Faza przyspieszenia:

$$
t_{\text{accel}} = \frac{m \times v_{\text{max}}}{F_{\text{avg}}}
$$

Gdzie \( F_{\text{avg}} \) maleje z powodu wolniejszego wzrostu ciśnienia.

Pomiar i walidacja

Wyniki testów przepływu:

W układzie Roberta w różnych temperaturach:

• +5°C: 45 SCFM przez zawór główny
• -10°C: 38 SCFM przez zawór główny (redukcja 16%)
• -25°C: 29 SCFM przez zawór główny (redukcja 36%)

Pomiar czasu reakcji:

• +5°C: średni czas reakcji cylindra 180 ms
• -10°C: średni czas reakcji cylindra 235 ms (+31%)
• -25°C: średni czas reakcji cylindra 295 ms (+64%)

Jak można mierzyć i przewidywać opóźnienia reakcji spowodowane temperaturą?

Dokładny pomiar i prognozowanie wpływu temperatury umożliwia proaktywną optymalizację systemu. 📊

Zmierz opóźnienia spowodowane temperaturą, używając szybkiego zbierania danych, żeby zapisać czas działania zaworu i ruchu cylindra w różnych zakresach temperatur, a potem stwórz modele prognostyczne, używając zależności między lepkością a przepływem oraz współczynników termicznych, żeby przewidzieć wydajność w różnych temperaturach roboczych.

Wymagania dotyczące konfiguracji pomiarowej

Niezbędne oprzyrządowanie:

• Czujniki temperatury: RTD⁵ lub termopary (dokładność ±0,5°C)
• Przetworniki ciśnienia: Szybka reakcja (<1 ms), wysoka dokładność
• Czujniki położenia: Enkodery liniowe lub czujniki zbliżeniowe
• Przepływomierze: Pomiar przepływu masowego lub objętościowego
• Pozyskiwanie danych: Szybkie próbkowanie (≥1 kHz)

Punkty pomiarowe:

• Temperatura otoczenia: Warunki środowiskowe
• Temperatura powietrza zasilającego: Temperatura sprężonego powietrza
• Temperatury komponentów: Zawory, cylindry, filtry
• Ciśnienia w systemie: Ciśnienie zasilania, robocze, wydechowe
• Pomiary czasu: Sygnał zaworu do zainicjowania ruchu

Metodologia testowania

Testy w kontrolowanej temperaturze:

1. Komora środowiskowa: Kontrola temperatury otoczenia
2. Równowaga termiczna: Odczekaj 30–60 minut na ustabilizowanie się.
3. Ustalenie wartości bazowej: Rekordowa wydajność w temperaturze odniesienia
4. Przebieg temperatury: Test w całym zakresie roboczym
5. Weryfikacja powtarzalności: Wielokrotne cykle w każdej temperaturze

Protokół testów terenowych:

1. Monitorowanie sezonowe: Długoterminowe gromadzenie danych
2. Codzienne cykle temperatur: Śledzenie zmian wydajności
3. Analiza porównawcza: Podobne systemy w różnych środowiskach
4. Zmiana obciążenia: Test w różnych warunkach pracy

Podejścia do modelowania predykcyjnego

Korelacja empiryczna:

$$
t_{\text{odpowiedź}}
= t_{\text{ref}} \times \left( \frac{\mu}{\mu_{\text{ref}}} \right)^{\alpha}
\times \left( \frac{T_{\text{ref}}}{T} \right)^{\beta}
$$

Gdzie \( \alpha \) i \( \beta \) są stałymi specyficznymi dla systemu, określonymi eksperymentalnie.

Model oparty na fizyce:

$$
t_{\text{response}} = t_{\text{valve}} + t_{\text{fill}} + t_{\text{accel}}
$$

Gdzie każdy składnik jest obliczany przy użyciu właściwości zależnych od temperatury.

Techniki walidacji modeli

Metoda walidacji	Dokładność	Zastosowanie	Złożoność
Testy laboratoryjne	±5%	Nowe projekty	Wysoki
Korelacja polowa	±10%	Istniejące systemy	Średni
Symulacja CFD	±15%	Optymalizacja projektu	Bardzo wysoka
Skalowanie empiryczne	±20%	Szybkie szacunki	Niski

Analiza danych i korelacja

Analiza statystyczna:

• Analiza regresjiOpracowanie korelacji między temperaturą a reakcją.
• Przedziały ufności: Kwantyfikacja niepewności prognozy
• Wykrywanie wartości odstających: Zidentyfikuj anomalne punkty danych.
• Analiza wrażliwości: Określ krytyczne zakresy temperatur

Mapowanie wydajności:

• Czas reakcji a temperatura: Relacja pierwotna
• Przepływ a temperatura: Wspieranie korelacji
• Wydajność a temperatura: Ocena wpływu na środowisko
• Niezawodność a temperaturaAnaliza wskaźnika awaryjności

Rozwój modelu predykcyjnego

Dla systemu chłodniczego Roberta:

Model czasu reakcji:
$$
t_{\text{odpowiedź}}(T)
= 180 × (T_(ref)/T)⁰,⁶⁵
\times \left( \frac{\mu(T)} {\mu_{\text{ref}}} \right)^{0,85}
$$

Wyniki walidacji:

• Współczynnik korelacji: R² = 0,94
• Średni błąd: ±8%
• Zakres temperaturod -25°C do +5°C
• Dokładność prognoz: ±15 ms w ekstremalnych temperaturach

Model natężenia przepływu:

$$
Q(T)
= Q_{\text{ref}} \times \left( \frac{T}{T_{\text{ref}}} \right)^{0,5}
\times \left( \frac{\mu_{\text{ref}}}{\mu(T)} \right)^{0,75}
$$

Wydajność modelu:

• Dokładność prognozowania przepływu: ±12%
• Korelacja spadku ciśnienia: R² = 0,91
• Optymalizacja systemu: Poprawa wydajności w niskich temperaturach o 25%

Systemy wczesnego ostrzegania

Alerty oparte na temperaturze:

• Spadek wydajności: >20% wydłużenie czasu reakcji
• Temperatura krytyczna: Poniżej -15°C dla tego systemu
• Analiza trendów: Wpływ tempa zmian temperatury
• Konserwacja predykcyjna: Harmonogram oparty na ekspozycji na temperaturę

Jakie rozwiązania mogą zminimalizować spadek wydajności w niskich temperaturach?

Łagodzenie skutków niskich temperatur wymaga kompleksowego podejścia obejmującego zarządzanie ciepłem, dobór komponentów i projektowanie systemów. 🛠️

Zminimalizuj spadek wydajności w niskich temperaturach poprzez ogrzewanie systemu (ogrzewane obudowy, ogrzewanie śladowe), optymalizację komponentów (większe kanały przepływowe, zawory niskotemperaturowe), kondycjonowanie płynów (osuszacze powietrza, regulacja temperatury) oraz dostosowanie systemu sterowania (kompensacja temperatury, wydłużony czas działania).

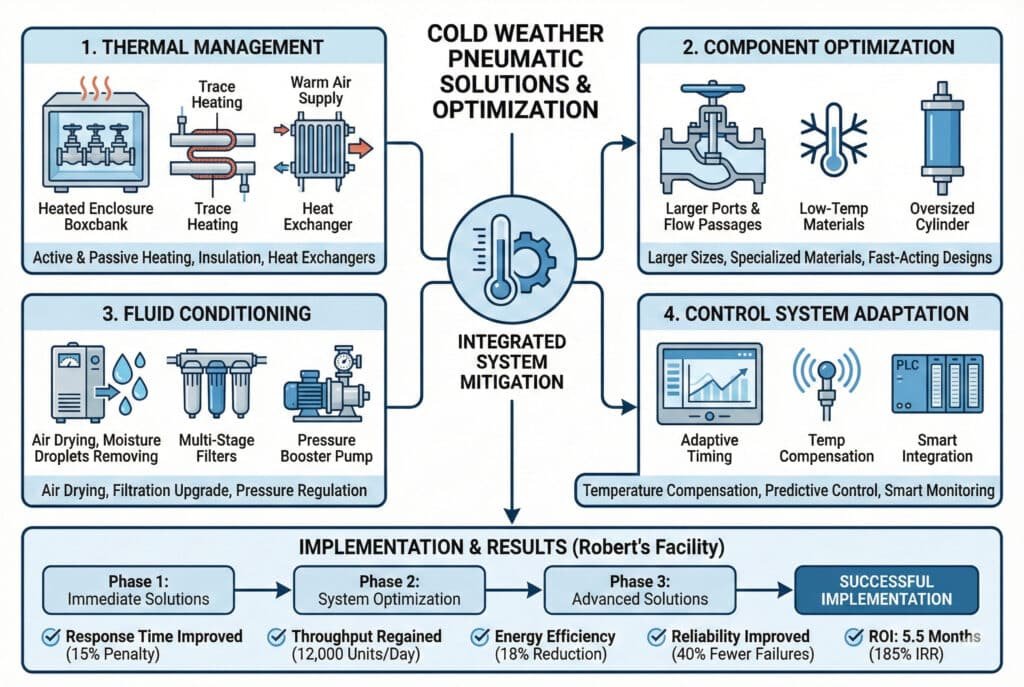
Rozwiązania w zakresie zarządzania temperaturą

Aktywne systemy grzewcze:

• Ogrzewane obudowy: Utrzymuj temperaturę komponentów powyżej krytycznych progów.
• Ogrzewanie śladowe: Elektryczne kable grzejne na przewodach pneumatycznych
• Wymienniki ciepła: Ciepłe napływające sprężone powietrze
• Izolacja termiczna: Ogranicz straty ciepła z elementów systemu

Pasywne zarządzanie temperaturą:

• Masa termicznaDuże elementy utrzymują temperaturę.
• Izolacja: Zapobieganie utracie ciepła do otoczenia
• Mostki termiczne: Odprowadzanie ciepła z obszarów ogrzewanych
• Ogrzewanie słoneczne: Wykorzystaj dostępną energię słoneczną

Optymalizacja komponentów

Wybór zaworu:

• Większe rozmiary portów: Zmniejszenie spadków ciśnienia wrażliwych na lepkość
• Materiały niskotemperaturowe: Zachowaj elastyczność w niskich temperaturach
• Szybko działające projekty: Minimalizuj straty czasu związane z przełączaniem
• Zintegrowane ogrzewanie: Wbudowana kompensacja temperatury

Modyfikacje projektu systemu:

• Elementy ponadgabarytowe: Kompensacja zmniejszonej wydajności przepływu
• Równoległe ścieżki przepływu: Zmniejsz ograniczenia dotyczące indywidualnych ścieżek
• Krótsze długości linii: Minimalizuj skumulowane spadki ciśnienia
• Zoptymalizowane trasy: Chronić przed narażeniem na zimno

Kondycjonowanie płynów

Rozwiązanie	Korzyści związane z temperaturą	Koszt wdrożenia	Skuteczność
Ogrzewanie powietrza	Wzrost o 15–25°C	Wysoki	Bardzo wysoka
Usuwanie wilgoci	Zapobiega zamarzaniu	Średni	Wysoki
Modernizacja filtracji	Utrzymuje przepływ	Niski	Średni
Wzrost ciśnienia	Pokonuje ograniczenia	Średni	Wysoki

Zaawansowane strategie sterowania

Kompensacja temperatury:

• Adaptacyjne taktowanie: Dostosuj czasy cyklu w oparciu o temperaturę.
• Profilowanie ciśnienia: Zwiększenie ciśnienia zasilania w niskich temperaturach
• Kompensacja przepływu: Zmiana rozrządu zaworów w celu uwzględnienia wpływu temperatury
• Kontrola predykcyjna: Przewiduj opóźnienia spowodowane temperaturą

Inteligentna integracja systemów:

• Monitorowanie temperatury: Ciągłe monitorowanie temperatury systemu
• Automatyczna regulacja: Kompensacja wpływu temperatury w czasie rzeczywistym
• Optymalizacja wydajności: Dynamiczne dostrajanie systemu
• Planowanie konserwacji: Okresy serwisowe oparte na temperaturze

Rozwiązania firmy Bepto na zimę

W firmie Bepto Pneumatics opracowaliśmy specjalistyczne rozwiązania do zastosowań w niskich temperaturach:

Innowacje projektowe:

• Butle do zimnych warunków pogodowych: Zoptymalizowany do pracy w niskich temperaturach
• Zintegrowane ogrzewanie: Wbudowane zarządzanie temperaturą
• Uszczelki niskotemperaturowe: Zachowaj elastyczność i szczelność
• Monitorowanie termiczne: Informacje zwrotne dotyczące temperatury w czasie rzeczywistym

Ulepszenia wydajności:

• Zbyt duże porty: 40% większy niż standardowy dla kompensacji lepkości
• Izolacja termiczna: Zintegrowane systemy izolacyjne
• Podgrzewane kolektory: Utrzymuj optymalną temperaturę komponentów.
• Inteligentne sterowanieAlgorytmy sterowania dostosowujące się do temperatury

Strategia wdrożeniowa dla obiektu Roberta

Faza 1: Natychmiastowe rozwiązania (tydzień 1–2)

• Montaż izolacji: Owinąć krytyczne elementy pneumatyczne
• Ogrzewane obudowy: Zamontować wokół kolektorów zaworów
• Ogrzewanie powietrza nawiewanegoWymiennik ciepła w instalacji sprężonego powietrza
• Regulacja sterowania: Wydłużenie czasu cyklu w okresach zimowych

Faza 2: Optymalizacja systemu (miesiąc 1-2)

• Aktualizacje komponentów: Wymień na zawory zoptymalizowane do pracy w niskich temperaturach.
• Modyfikacje linii: Przewody pneumatyczne o większej średnicy
• Ulepszenia filtracji: Filtry o wysokim przepływie i niskim oporze
• System monitorowania: Śledzenie temperatury i wydajności

Faza 3: Zaawansowane rozwiązania (miesiąc 3–6)

• Inteligentne sterowanie: System sterowania z kompensacją temperatury
• Algorytmy predykcyjne: Przewiduj i kompensuj wpływ temperatury
• Optymalizacja energetyczna: Równoważenie kosztów ogrzewania z poprawą wydajności
• Optymalizacja konserwacji: Planowanie usług w oparciu o temperaturę

Wyniki i poprawa wydajności

Wyniki wdrożenia Roberta:

• Poprawa czasu reakcji: Zmniejszenie kary za niską temperaturę z 65% do 15%
• Odzyskiwanie przepustowości: Odzyskano 12 000 z 15 000 utraconych jednostek dziennie.
• Efektywność energetyczna: 18% redukcja zużycia sprężonego powietrza
• Poprawa niezawodności: 40% zmniejszenie liczby awarii w niskich temperaturach

Analiza kosztów i korzyści

Koszty wdrożenia:

• Systemy grzewcze: $45,000
• Aktualizacje komponentów: $28,000
• System sterowania: $15,000
• Instalacja/uruchomienie: $12,000
• Inwestycje ogółem: $100,000

Roczne świadczenia:

• Ożywienie produkcji: $180 000 (poprawa przepustowości)
• Oszczędność energii: $25 000 (wzrost wydajności)
• Redukcja kosztów utrzymania: $15 000 (mniej awarii w niskich temperaturach)
• Całkowita roczna korzyść: $220,000

Analiza zwrotu z inwestycji:

• Okres zwrotu: 5,5 miesiąca
• 10-letnia wartość bieżąca netto: $1,65 mln
• Wewnętrzna stopa zwrotu: 185%

Konserwacja i monitorowanie

Konserwacja zapobiegawcza:

• Przygotowanie sezonowe: Optymalizacja systemu przed zimą
• Monitorowanie temperatury: Ciągłe śledzenie wydajności
• Kontrola podzespołów: Regularna kontrola systemów grzewczych
• Weryfikacja wydajności: Sprawdź skuteczność kompensacji temperatury.

Optymalizacja długoterminowa:

• Analiza danych: Ciągłe doskonalenie w oparciu o dane dotyczące wydajności
• Aktualizacje systemu: Ewolucja integracji technologii
• Programy szkoleniowe: Szkolenie operatorów w zakresie wpływu temperatury
• Najlepsze praktyki: Dokumentacja i dzielenie się wiedzą

Kluczem do pomyślnego działania w niskich temperaturach jest zrozumienie, że wpływ temperatury można przewidzieć i kontrolować poprzez odpowiednią inżynierię i projektowanie systemów. 🎯

Często zadawane pytania dotyczące lepkości płynów i wpływu niskich temperatur

1. Dowiedz się więcej o konkretnej stałej wywodzącej się z przyciągania międzycząsteczkowego, wykorzystywanej do obliczania lepkości gazu. ↩

2. Poznaj teorię wyjaśniającą makroskopowe właściwości gazów w oparciu o ruch cząsteczek. ↩

3. Dowiedz się więcej o bezwymiarowej wielkości, która pozwala przewidzieć wzorce przepływu płynów. ↩

4. Zrozumienie płynnego, równoległego reżimu przepływu, który dominuje przy niskich prędkościach. ↩

5. Zapoznaj się z zasadą działania czujników temperatury oporowych, aby uzyskać precyzyjne pomiary temperatury. ↩