Imate težave z uhajanjem zraka v svojih pnevmatskih sistemih? Niste sami. Veliko inženirjev se spopada z napakami tesnil, ki povzročajo izgubo učinkovitosti, višje stroške vzdrževanja in nepričakovane zastoje. S pravim znanjem o mehanizmih tesnjenja lahko rešite te trdovratne težave.
Tesnilni mehanizmi v pnevmatskih sistemih delujejo z nadzorovano deformacijo elastomerni materiali1 ob stičnih površinah. Učinkovita tesnila vzdržujejo kontaktni tlak s stiskanjem (statična tesnila) ali z ravnovesjem tlaka, trenja in mazanja (dinamična tesnila), kar ustvarja neprepustno pregrado proti uhajanju zraka.
V podjetju Bepto že več kot 15 let delam s pnevmatskimi sistemi in videl sem nešteto primerov, ko je razumevanje načel tesnjenja podjetjem prihranilo na tisoče stroškov vzdrževanja in preprečilo katastrofalne okvare sistema.
Kazalo vsebine
- Kako razmerje kompresije O-obroča vpliva na učinkovitost tesnila?
- Zakaj je Stribeckova krivulja bistvena za načrtovanje pnevmatskega tesnila?
- Kaj povzroča segrevanje zaradi trenja v dinamičnih tesnilih in kako ga je mogoče nadzorovati?
- Zaključek
- Pogosta vprašanja o mehanizmih pnevmatskega tesnjenja
Kako razmerje kompresije O-obroča vpliva na učinkovitost tesnila?
O-obročki so morda najpogostejši tesnilni elementi v pnevmatskih sistemih, vendar se za njihovim preprostim videzom skrivajo zapletena inženirska načela. Kompresijsko razmerje je ključnega pomena za njihovo učinkovitost in dolgo življenjsko dobo.
Stopnja stiskanja O-obroča je odstotek deformacije glede na prvotni prerez ob namestitvi. Za optimalno delovanje je običajno potrebna kompresija 15-30%. Premajhna kompresija povzroči puščanje, prevelika kompresija pa predčasno okvaro zaradi iztiskanja, komplet za stiskanje2ali pospešeno obrabo.

Pravilno kompresijsko razmerje je bolj zapleteno, kot se mnogi inženirji zavedajo. Naj z vami delim nekaj praktičnih spoznanj iz svojih izkušenj s sistemi za tesnjenje valjev brez palice.
Izračun optimalnega razmerja stiskanja O-obročev
Izračun kompresijskega razmerja se zdi preprost:
| Parameter | Formula | Primer |
|---|---|---|
| Kompresijsko razmerje (%) | [(d - g)/d] × 100 | Za 2,5-milimetrski O-obroč v 2,0-milimetrskem utoru: [(2,5 - 2,0)/2,5] × 100 = 20% |
| Stisk (mm) | d - g | 2,5 mm - 2,0 mm = 0,5 mm |
| Zapolnitev utorov (%) | [π(d/2)²]/[w × g] × 100 | Za 2,5-milimetrski O-obroč v 3,5 mm širokem in 2,0 mm globokem utoru: [π(2,5/2)²]/[3,5 × 2,0] × 100 = 70% |
Kje:
- d = premer prečnega prereza O-obroča
- g = globina utora
- w = širina utora
Smernice za stiskanje, specifične za material
Za različne materiale so potrebna različna kompresijska razmerja:
| Material | Priporočena kompresija | Aplikacija |
|---|---|---|
| NBR (nitril) | 15-25% | Splošna uporaba, odpornost na olje |
| FKM (Viton) | 15-20% | Visoka temperatura, kemična odpornost |
| EPDM | 20-30% | Uporaba vode, pare |
| Silikon | 10-20% | Ekstremna temperaturna območja |
| PTFE | 5-10% | Kemijska odpornost, nizko trenje |
Lani sem delal z Michaelom, inženirjem za vzdrževanje v obratu za predelavo hrane v Wisconsinu. Kljub uporabi vrhunskih O-obročev je v svojih sistemih brez paličnih jeklenk pogosto puščal zrak. Po analizi njegove namestitve sem odkril, da je njegova zasnova utorov povzročala prekomerno stiskanje (skoraj 40%) O-obročev NBR.
Preoblikovali smo dimenzije utorov, da smo dosegli kompresijsko razmerje 20%, življenjska doba tesnila pa se je s 3 mesecev podaljšala na več kot eno leto, s čimer je podjetje prihranilo več tisoč evrov pri stroških vzdrževanja in izostankih.
Okoljski dejavniki, ki vplivajo na zahteve glede stiskanja
Optimalno razmerje stiskanja ni statično - spreminja se glede na:
- Temperaturna nihanja: Pri višjih temperaturah je zaradi toplotnega raztezanja potrebna manjša kompresija.
- Tlačne razlike: Pri višjih tlakih bo morda potrebna večja kompresija, da se prepreči iztiskanje.
- Dinamične in statične aplikacije: Dinamična tesnila običajno potrebujejo manjšo kompresijo, da se zmanjša trenje.
- Načini namestitve: Razteg med namestitvijo lahko zmanjša učinkovito stiskanje
Zakaj je Stribeckova krivulja bistvena za načrtovanje pnevmatskega tesnila?
Stribeckova krivulja se morda sliši akademsko, vendar je v resnici močno praktično orodje za razumevanje in optimizacijo delovanja tesnil v brezročnih pnevmatskih cilindrih in drugih dinamičnih aplikacijah.
Spletna stran Stribeckova krivulja3 prikazuje povezavo med koeficientom trenja, viskoznostjo maziva, hitrostjo in obremenitvijo na drsnih površinah. Pri pnevmatskih tesnilih inženirjem pomaga razumeti prehod med mejnimi, mešanimi in hidrodinamičnimi režimi mazanja, kar je ključnega pomena za optimizacijo zasnove tesnila za posebne delovne pogoje.
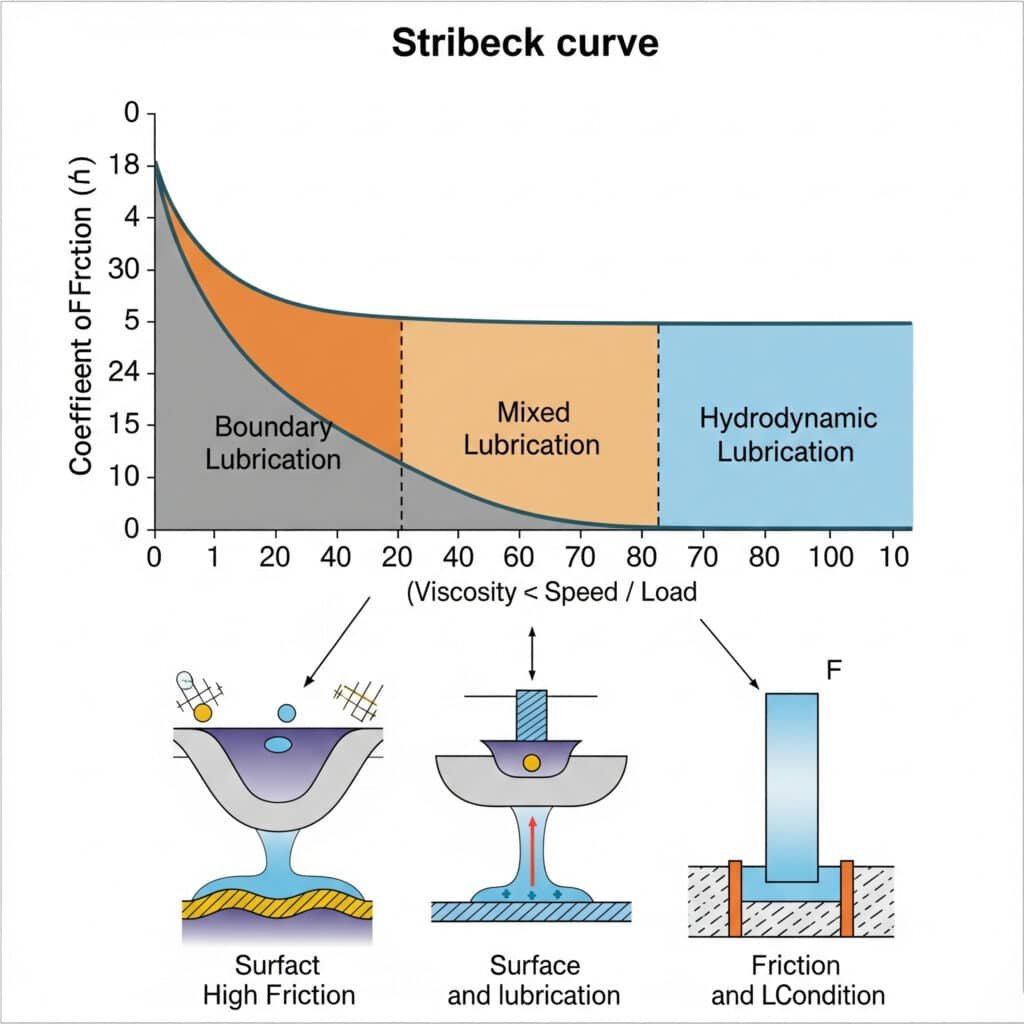
Razumevanje te krivulje ima praktične posledice za delovanje pnevmatskih sistemov v realnih razmerah.
Trije režimi mazanja v pnevmatskih tesnilih
Stribeckova krivulja opredeljuje tri različne režime delovanja:
| Režim mazanja | Značilnosti | Posledice za pnevmatska tesnila |
|---|---|---|
| Mejno mazanje | Visoko trenje, neposreden stik s površino | Pojavi se med zagonom, pri nizkih hitrostih; povzroča zdrs palice |
| Mešano mazanje | Zmerno trenje, delna plast tekočine | Prehodno območje; občutljivo na obdelavo površine in mazivo |
| Hidrodinamično mazanje4 | Majhno trenje, popolno ločevanje tekočin | Idealno za delo pri visoki hitrosti; minimalna obraba |
Praktična uporaba Stribeckove krivulje pri izbiri tesnil
Pri izbiri tesnil za cilindre brez palic nam je v pomoč razumevanje Stribeckove krivulje:
- Ujemanje materialov tesnil z delovnimi pogoji: Različni materiali se bolje obnesejo pri različnih režimih mazanja
- Izberite ustrezna maziva: Zahteve glede viskoznosti se spreminjajo glede na hitrost in obremenitev
- Oblikovanje optimalnih površinskih obdelav: Hrapavost vpliva na prehod med režimi mazanja
- Napovedovanje in preprečevanje pojavov zdrsa: ključnega pomena za nemoteno delovanje v natančnih aplikacijah.
Študija primera: Odprava zdrsa pri natančnem pozicioniranju
Spomnim se sodelovanja z Emmo, inženirko avtomatizacije pri proizvajalcu medicinskih pripomočkov v Švici. Pri njenem sistemu valjev brez palic je pri natančnih premikih z majhno hitrostjo prihajalo do poskočnega gibanja (stick-slip), kar je vplivalo na kakovost izdelka.
Z analizo aplikacije s pomočjo Stribeckove krivulje smo ugotovili, da je njen sistem deloval v režimu mejnega mazanja. Priporočili smo zamenjavo tesnilnega materiala na osnovi PTFE s spremenjeno strukturo površine in drugačno sestavo maziva.
Rezultat? Gladko gibanje tudi pri hitrosti 5 mm/sekundo, kar odpravlja težave s kakovostjo in izboljšuje donos proizvodnje za 15%.
Kaj povzroča segrevanje zaradi trenja v dinamičnih tesnilih in kako ga je mogoče nadzorovati?
Segrevanje zaradi trenja je pogosto spregledano, dokler ne povzroči prezgodnje okvare tesnila. Razumevanje tega pojava je bistveno za načrtovanje zanesljivih pnevmatskih sistemov s podaljšano življenjsko dobo.
Ogrevanje s trenjem5 v dinamičnih tesnilih nastane, ko se mehanska energija pretvori v toplotno energijo na kontaktnem vmesniku med tesnilom in stično površino. Na to segrevanje vplivajo dejavniki, kot so hitrost površine, kontaktni tlak, mazanje in lastnosti materiala. Prekomerno segrevanje pospešuje razgradnjo tesnila zaradi toplotnega razkroja materialov.
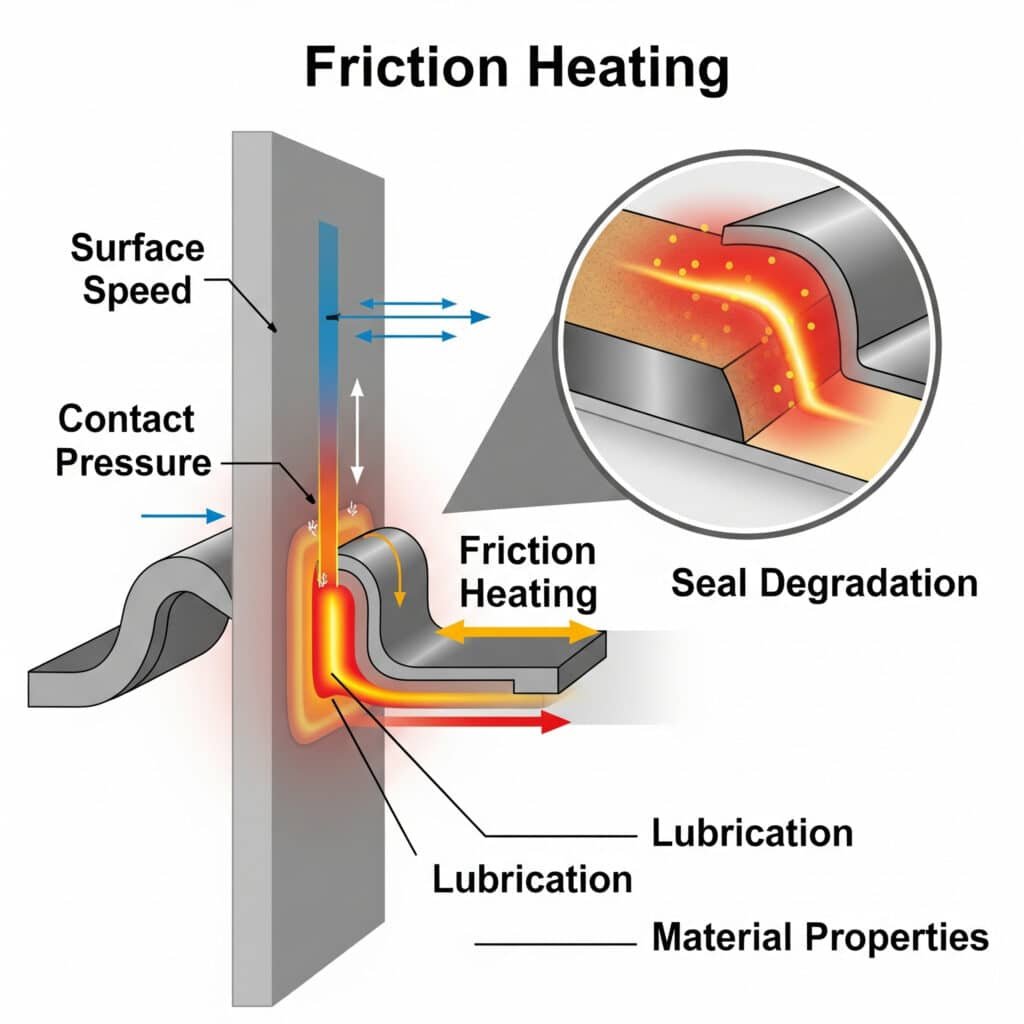
Posledice segrevanja zaradi trenja so lahko hude, od skrajšane življenjske dobe tesnil do katastrofalne okvare. Podrobneje preučimo ta pojav.
Kvantifikacija ustvarjanja torne toplote
Toploto, ki nastane zaradi trenja, lahko ocenimo z uporabo:
| Parameter | Formula | Primer |
|---|---|---|
| Proizvodnja toplote (W) | Q = μ × F × v | Za μ=0,2, F=100N, v=0,5m/s: Q = 0,2 × 100 × 0,5 = 10W |
| Dvig temperature (°C) | ΔT = Q/(m × c) | Za 10 W toplote, 5 g tesnila, c=1,7J/g°C: ΔT = 10/(5 × 1,7) = 1,18 °C/s |
| Temperatura v ustaljenem stanju | Tss = Ta + (Q/hA) | Odvisno od koeficienta prenosa toplote in površine |
Kje:
- μ = koeficient trenja
- F = normalna sila
- v = hitrost drsenja
- m = masa
- c = specifična toplotna kapaciteta
- Ta = temperatura okolice
- h = koeficient prenosa toplote
- A = površina
Kritične temperaturne meje za običajne tesnilne materiale
Različni tesnilni materiali imajo različne temperaturne omejitve:
| Material | Najvišja trajna temperatura (°C) | Znaki toplotne degradacije |
|---|---|---|
| NBR (nitril) | 100-120 | Strjevanje, razpokanje, zmanjšana elastičnost |
| FKM (Viton) | 200-250 | Razbarvanje, zmanjšana prožnost |
| PTFE | 260 | Spremembe dimenzij, zmanjšana natezna trdnost |
| TPU | 80-100 | Mehčanje, deformacija, razbarvanje |
| UHMW-PE | 80-90 | Deformacije, zmanjšana odpornost proti obrabi |
Strategije za zmanjšanje segrevanja zaradi trenja
Na podlagi mojih izkušenj z uporabo valjev brez palice so navedene učinkovite strategije za nadzor segrevanja zaradi trenja:
- Optimizacija kontaktnega tlaka: Zmanjšajte posege v tesnilo, kjer je to mogoče, ne da bi pri tem ogrozili tesnenje.
- Izboljšanje mazanja: Izberite maziva z ustrezno viskoznostjo in temperaturno stabilnostjo.
- Izbira materiala: Izberite materiale z nižjimi koeficienti trenja in večjo toplotno stabilnostjo.
- Površinski inženiring: Določite ustrezno obdelavo površine in premaze za zmanjšanje trenja.
- Zasnova odvajanja toplote: Vključujejo značilnosti, ki izboljšujejo prenos toplote stran od tesnil.
Uporaba v resničnem svetu: Zasnova cilindra brez palice za visoke hitrosti
Ena od naših strank v Nemčiji uporablja opremo za pakiranje pri visokih hitrostih s cilindri brez palic, ki delujejo pri hitrostih do 2 m/s. Njihova originalna tesnila so zaradi segrevanja zaradi trenja odpovedala že po 3 milijonih ciklov.
Opravili smo toplotno analizo in odkrili, da je temperatura na vmesniku tesnila dosegla 140 °C - precej več, kot je meja 100 °C za njihova tesnila NBR. S prehodom na kompozitno tesnilo iz PTFE z optimizirano geometrijo stika in izboljšanjem odvajanja toplote v cilindru smo podaljšali življenjsko dobo tesnila na več kot 20 milijonov ciklov.
Zaključek
Razumevanje znanstvenega ozadja kompresijskih razmerij O-obročev, praktične uporabe Stribeckove krivulje in mehanizmov segrevanja zaradi trenja je osnova za načrtovanje zanesljivih in dolgotrajnih pnevmatskih tesnilnih sistemov. Z uporabo teh načel lahko izberete prava tesnila za svoje aplikacije brezročnih cilindrov, odpravite obstoječe težave in preprečite drage okvare, še preden se pojavijo.
Pogosta vprašanja o mehanizmih pnevmatskega tesnjenja
Kakšno je idealno kompresijsko razmerje za O-obroče v pnevmatskih aplikacijah?
Idealno kompresijsko razmerje za O-obroče v pnevmatskih aplikacijah je običajno 15-25% za statična tesnila in 10-20% za dinamična tesnila. Ta razpon zagotavlja zadostno tesnilno silo in hkrati preprečuje pretirano stiskanje, ki bi lahko vodilo do prezgodnje okvare, zlasti v aplikacijah z valji brez palic.
Kako Stribeckova krivulja pomaga pri izbiri pravega tesnila za mojo aplikacijo?
Stribeckova krivulja pomaga določiti, v katerem režimu mazanja bo delovala vaša aplikacija glede na hitrost, obremenitev in lastnosti maziva. Za aplikacije z nizko hitrostjo in visoko obremenitvijo izberite tesnila, optimizirana za mejno mazanje. Za visokohitrostne aplikacije izberite tesnila, zasnovana za hidrodinamično mazanje.
Kaj povzroča drsenje v pnevmatskih cilindrih in kako ga je mogoče preprečiti?
Drsenje s palico je posledica razlike med statičnimi in dinamičnimi koeficienti trenja, zlasti v režimu mejnega mazanja. Preprečite ga z uporabo tesnilnih materialov na osnovi PTFE ali drugih materialov z nizkim trenjem, uporabo ustreznih maziv, optimizacijo površinske obdelave in zagotavljanjem ustreznega stiskanja tesnil za vaše cilindre brez palice.
Kako veliko povečanje temperature je sprejemljivo za dinamična tesnila?
Sprejemljivo povišanje temperature je odvisno od materiala tesnila. Splošno pravilo je, da naj bo delovna temperatura vsaj 20 °C nižja od najvišje nazivne trajne temperature materiala. Za tesnila iz NBR (nitrila), ki so pogosta v cilindrih brez palic, naj bodo temperature nižje od 80-100 °C, da se podaljša življenjska doba.
Kakšna je povezava med trdoto tesnila in zahtevami glede stiskanja?
Trdši tesnilni materiali (višji durometer) običajno zahtevajo manjši pritisk, da se doseže učinkovito tesnjenje. Na primer, material s trdnostjo 90 Shore A lahko potrebuje le 10-15% stiskanja, medtem ko mehkejši material s trdnostjo 70 Shore A za enako učinkovitost tesnjenja v pnevmatskih aplikacijah potrebuje 20-25% stiskanja.
Kako izračunam dimenzije utorov za O-obročno tesnilo?
Dimenzije utorov izračunajte tako, da določite zahtevano kompresijsko razmerje za vašo uporabo in material. Za standardno stiskanje 25% 2,5-milimetrskega O-obroča je globina utora 1,875 mm (2,5 mm × 0,75). Širina utora mora omogočati zapolnitev utora 60-85%, da se omogoči nadzorovana deformacija brez prevelikih obremenitev.
-
Podaja temeljno razlago elastomerov (polimerov z viskoelastičnostjo), ki se zaradi svoje sposobnosti deformacije in vračanja v prvotno obliko uporabljajo kot glavni materiali za pnevmatska tesnila. ↩
-
Ponuja tehnično opredelitev kompresijskega posedanja, trajne deformacije tesnila po dolgotrajni tlačni obremenitvi, ki je glavni vzrok za statično okvaro tesnila. ↩
-
Podrobno predstavi načela Stribeckove krivulje, temeljnega grafa na področju tribologije, ki ponazarja, kako je trenje med dvema mazanima površinama odvisno od viskoznosti, obremenitve in hitrosti. ↩
-
Razloži režim hidrodinamičnega mazanja, idealnega stanja, v katerem polna, neprekinjena tekočinska plast popolnoma ločuje dve gibajoči se površini, zaradi česar sta trenje in obraba minimalna. ↩
-
Opisuje fiziko segrevanja zaradi trenja, procesa, pri katerem se mehanska energija pretvori v toplotno na drsnem vmesniku, kar je ključni dejavnik pri toplotni degradaciji dinamičnih tesnil. ↩



