Nočna mora vsakega inženirja vzdrževanja je nepričakovana okvara opreme. Kadar stroji vibrirajo pri svoji naravni frekvenci, lahko v nekaj minutah pride do katastrofalnih poškodb. Videl sem, da je ta težava podjetja stala na tisoče evrov zaradi izpadov.
Vibracijska resonanca1 nastane, ko se zunanja sila ujema z naravno frekvenco sistema, kar povzroči okrepljena nihanja, ki lahko poškodujejo opremo. Razumevanje in nadzor tega pojava sta bistvena za preprečevanje okvar in podaljšanje življenjske dobe strojev.
Naj vam na kratko povem zgodbo. Lani me je stranka iz Nemčije poklicala v paniki. Njihova proizvodna linija se je ustavila zaradi valj brez palice je močno vibriral. Težava? Resonanca. Do konca tega članka boste razumeli, kako prepoznati in preprečiti podobne težave v svojih sistemih.
Kazalo vsebine
- Formula naravne frekvence: Kako lahko izračunate ranljive točke vašega sistema?
- Model Mass-Spring: Zakaj je ta poenostavljeni pristop tako dragocen?
- Optimizacija dušilnega razmerja: Kateri poskusi dajejo najboljše rezultate?
- Zaključek
- Pogosta vprašanja o vibracijski resonanci
Formula naravne frekvence: Kako lahko izračunate ranljive točke vašega sistema?
Poznavanje naravne frekvence opreme je prvi korak k preprečevanju težav z resonanco. Ta kritična vrednost določa, kdaj je vaš sistem najbolj izpostavljen težavam z vibracijami.
Spletna stran lastna frekvenca2 (fn) sistema lahko izračunamo po formuli: fn = (1/2π) × √(k/m), kjer je k koeficient togosti, m pa masa. Ta izračun pokaže frekvenco, pri kateri bo vaš sistem resoniral, če ga bodo vzbujale ustrezne zunanje sile.
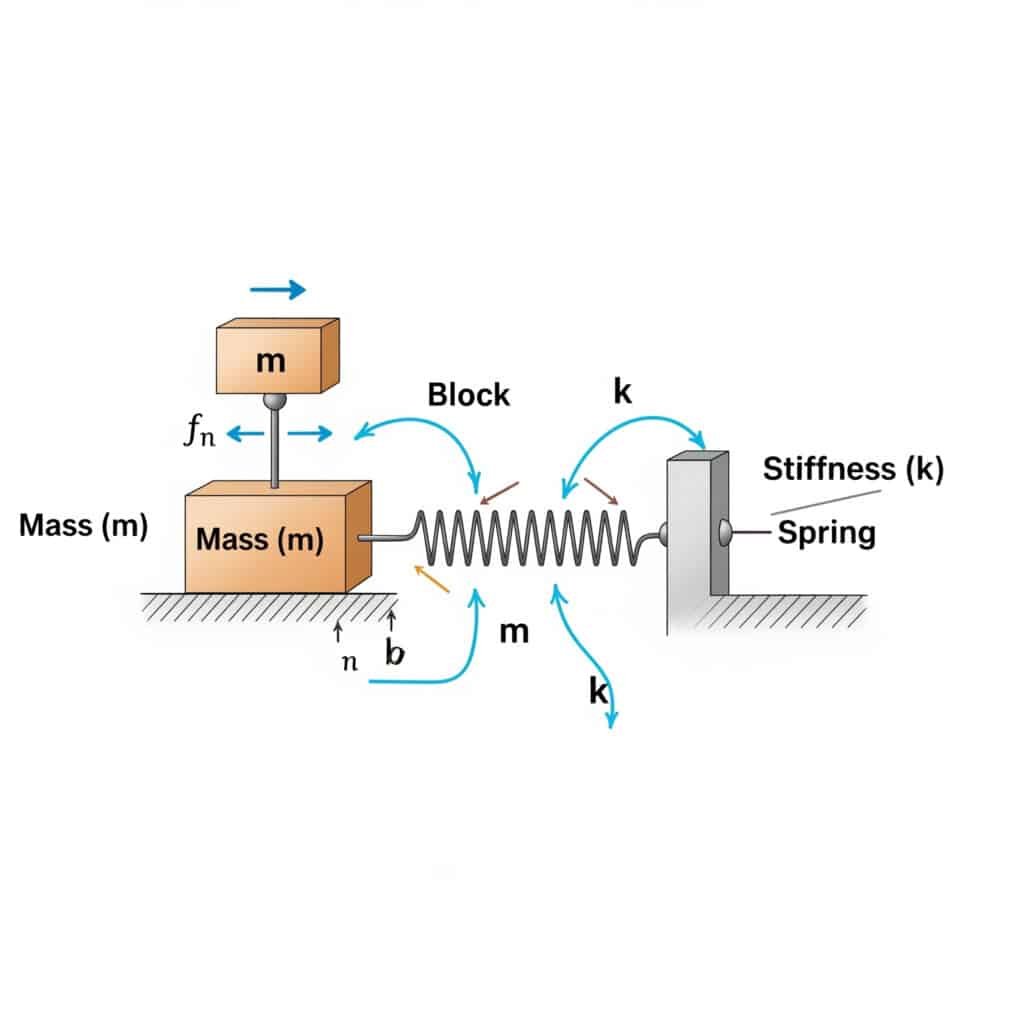
Ko sem obiskal proizvodni obrat v Švici, sem opazil, da se njihovi pnevmatski cilindri brez palice prezgodaj kvarijo. Njihova ekipa za vzdrževanje ni izračunala naravne frekvence njihove postavitve. Po uporabi te formule smo ugotovili, da je bila njihova delovna hitrost nevarno blizu naravne frekvence sistema.
Praktična uporaba izračunov lastne frekvence
Formula za naravno frekvenco ni le teoretična - neposredno se uporablja v različnih industrijskih okoljih:
- Izbira opreme: Izbira komponent z lastnimi frekvencami, ki so daleč od vaših delovnih pogojev
- Preventivno vzdrževanje: Načrtovanje pregledov na podlagi profilov tveganja vibracij
- Odpravljanje težav: Ugotavljanje osnovnega vzroka nepričakovanih vibracij
Običajne vrednosti lastne frekvence za industrijske komponente
| Komponenta | Tipično območje naravne frekvence (Hz) |
|---|---|
| Cilindri brez palic | 10-50 Hz |
| Montažni nosilci | 20-100 Hz |
| Podporne strukture | 5-30 Hz |
| Regulacijski ventili | 40-200 Hz |
Kritični dejavniki, ki vplivajo na naravno frekvenco
Izračun lastne frekvence se zdi preprost, vendar lahko več dejavnikov oteži uporabo v resničnem svetu:
- Neenakomerna porazdelitev mase: Večina industrijskih komponent nima popolnoma porazdeljene mase
- Spremenljiva togost: Komponente imajo lahko različno togost v različnih smereh.
- Priključne točke: Način pritrditve sestavnih delov pomembno vpliva na njihove lastnosti vibracij.
- Vpliv temperature: Lastnosti mase in togosti se lahko spreminjajo s temperaturo.
Model Mass-Spring: Zakaj je ta poenostavljeni pristop tako dragocen?
Model mase in vzmeti zagotavlja intuitiven okvir za razumevanje kompleksnih vibracijskih sistemov. Zapletene stroje zmanjša na osnovne elemente, ki jih inženirji zlahka analizirajo.
Spletna stran model mase in vzmeti3 poenostavi analizo vibracij, saj mehanske sisteme predstavlja kot diskretne mase, povezane z vzmetmi. Ta pristop inženirjem omogoča napovedovanje obnašanja sistema, ugotavljanje morebitnih resonančnih težav in razvoj učinkovitih rešitev brez zapletene matematike.
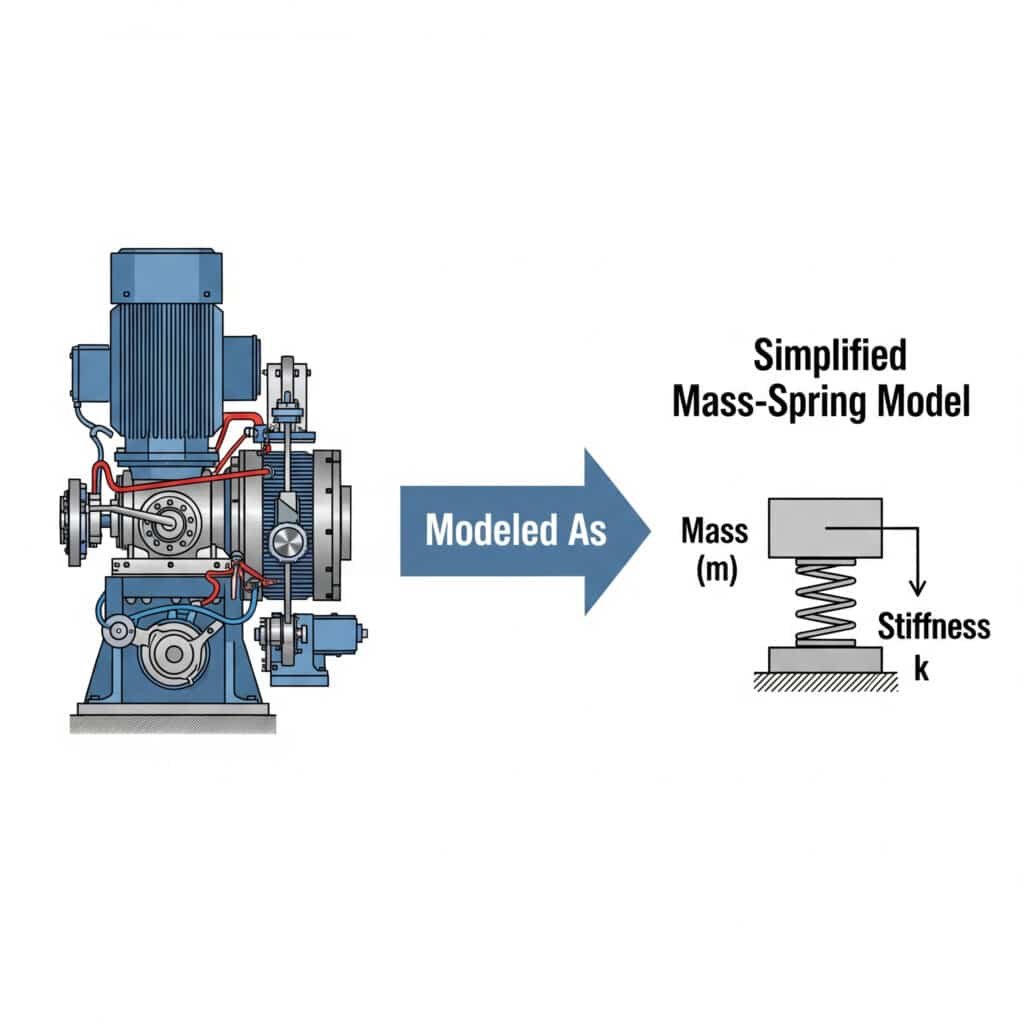
Spomnim se sodelovanja s proizvajalcem avtomobilskih delov v Michiganu, ki ni mogel razumeti, zakaj njegovi vodeni cilindri brez palic odpovedujejo. Z modeliranjem njihovega sistema kot preproste ureditve mase in vzmeti smo ugotovili, da so montažni nosilci delovali kot nenamerne vzmeti in ustvarjali resonančno stanje.
Pretvarjanje realnih sistemov v modele masne vzmeti
Če želite ta pristop uporabiti za svojo opremo:
- Opredelitev ključnih množic: Ugotovite, kateri sestavni deli prispevajo pomembno težo
- Poiščite vzmetne elemente: Poiščite komponente, ki shranjujejo in sproščajo energijo (dejanske vzmeti, prožni nosilci itd.)
- Povezave na zemljevidu: Dokumentirajte interakcijo med masami in vzmetmi.
- Poenostavite: Združite podobne elemente, da ustvarite obvladljiv model.
Vrste sistemov z masnim vzmetenjem
| Vrsta sistema | Opis | Pogoste aplikacije |
|---|---|---|
| Posamezni DOF | Ena masa z eno vzmetjo | Enostavni pnevmatski cilindri |
| Multi-DOF | Več mas z več vzmetmi | Kompleksni stroji z več sestavnimi deli |
| Neprekinjeno | Neskončno DOF (zahteva drugačno analizo) | Nosilci, plošče in lupine |
Razmisleki o naprednem modeliranju
Čeprav je osnovni model z masno vzmetjo dragocen, ga več izboljšav naredi bolj realističnega:
- Dodajanje blažilnikov: V realnih sistemih vedno prihaja do razpršitve energije
- Upoštevanje nelinearnosti: Vzmeti ne sledijo vedno Hookov zakon4 popolnoma
- Obračunavanje prisilnih vibracij: Zunanje sile spreminjajo obnašanje sistema
- Vključno z učinki spajanja: Gibanje v eni smeri lahko vpliva na druge smeri.
Optimizacija dušilnega razmerja: Kateri poskusi dajejo najboljše rezultate?
Dušenje je najboljša zaščita pred težavami z resonanco. Z eksperimentiranjem lahko poiščete optimalno razmerje dušenja in s tem bistveno izboljšate zmogljivost in zanesljivost sistema.
Razmerje dušenja5 optimizacijski poskusi vključujejo sistematično preizkušanje različnih konfiguracij dušenja, da bi našli idealno ravnovesje med nadzorom vibracij in odzivnostjo sistema. Optimalno razmerje dušenja je običajno med 0,2 in 0,7, kar zagotavlja zadostno dušenje vibracij brez pretirane izgube energije.
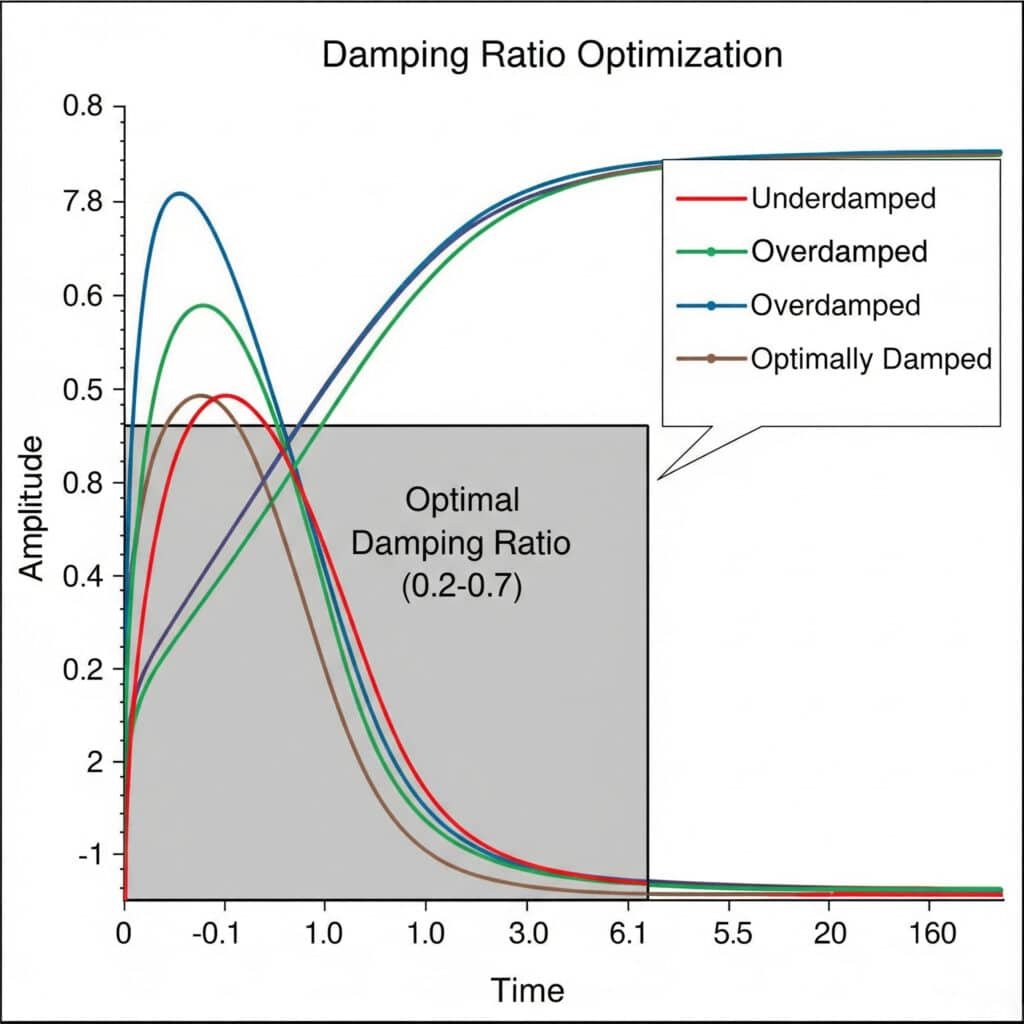
Prejšnji mesec sem proizvajalcu opreme za predelavo hrane v Franciji pomagal rešiti težave z nenehnimi vibracijami v njihovih magnetnih valjih brez palice. Z vrsto poskusov z dušilnim razmerjem smo ugotovili, da je bilo dušilno razmerje njihove prvotne zasnove le 0,05 - daleč premajhno, da bi preprečilo težave z resonanco.
Eksperimentalna postavitev za preskušanje dušilnega razmerja
Izvajanje poskusov za optimizacijo učinkovitega dušenja:
- Osnovno merjenje: Odziv sistema brez dodatnega dušenja
- Inkrementalno testiranje: Dodajanje dušilnih elementov v nadzorovanih korakih
- Merjenje odziva: Merjenje amplitude, časa umirjanja in frekvenčnega odziva
- Analiza podatkov: Izračunajte razmerje dušenja za vsako konfiguracijo
- Potrjevanje: Preverite delovanje v dejanskih delovnih pogojih.
Primerjava tehnologij blaženja
| Tehnologija blaženja | Prednosti | Omejitve | Tipične aplikacije |
|---|---|---|---|
| Viskozni blažilniki | Predvidljivo delovanje, stabilna temperatura | Zahteva vzdrževanje, možnost puščanja | Težki stroji, natančna oprema |
| Blažilniki trenja | Enostavna zasnova, stroškovna učinkovitost | Obraba s časom, nelinearno obnašanje | Konstrukcijski nosilci, osnovni stroji |
| Dušenje materiala | Brez gibljivih delov, kompakten | Omejeno območje nastavitev | Natančni instrumenti, izolacija vibracij |
| Aktivno blaženje | Prilagodljivost spreminjajočim se razmeram | Kompleksno, zahteva moč | Kritične aplikacije, oprema s spremenljivo hitrostjo |
Optimizacija dušenja za različne delovne pogoje
Idealno razmerje dušenja ni univerzalno - odvisno je od konkretne uporabe:
- Poslovanje z visoko hitrostjo: Nižja razmerja dušenja (0,1-0,3) ohranjajo odzivnost
- Natančne aplikacije: Večja razmerja dušenja (0,5-0,7) zagotavljajo stabilnost
- Sistemi s spremenljivo obremenitvijo: Morda bo potrebno prilagodljivo dušenje
- Okolja, občutljiva na temperaturo: Upoštevajte dušilne materiale s stabilnimi lastnostmi
Študija primera: Optimizacija dušenja valjev brez palic
Pri optimizaciji cilindra brez palice z dvojnim delovanjem za stroj za pakiranje smo preizkusili pet različnih konfiguracij dušenja:
- Standardne čelne blazine: Koeficient dušenja = 0,12
- Podaljšane blazine: Koeficient dušenja = 0,25
- Zunanji amortizerji: Koeficient dušenja = 0,41
- Sestavljeni montažni nosilci: Koeficient dušenja = 0,38
- Kombinirani pristop (3+4): Koeficient dušenja = 0,53
Kombinirani pristop je zagotovil najboljšo učinkovitost, saj je zmanjšal amplitudo vibracij za 78%, hkrati pa ohranil sprejemljive odzivne čase.
Zaključek
Razumevanje resonance vibracij z izračuni lastne frekvence, modeliranjem masnih vzmeti in optimizacijo dušilnega razmerja je ključnega pomena za preprečevanje okvar opreme. Z uporabo teh načel lahko podaljšate življenjsko dobo strojev, skrajšate izpade in izboljšate splošno zmogljivost sistema.
Pogosta vprašanja o vibracijski resonanci
Kaj je resonanca vibracij v industrijski opremi?
Vibracijska resonanca nastane, ko se zunanja sila ujema z lastno frekvenco sistema, kar povzroči okrepljeno nihanje. V industrijski opremi lahko ta pojav privede do prekomernega gibanja, utrujanja sestavnih delov in katastrofalnih okvar, če ni ustrezno upravljan.
Kako lahko ugotovim, ali v mojem sistemu prihaja do resonance?
Poiščite simptome, kot so nepojasnjeno povečanje hrupa, vidne vibracije pri določenih hitrostih, prezgodnje okvare sestavnih delov in poslabšanje zmogljivosti, ki se pojavlja pri enakih obratovalnih točkah. Orodja za analizo vibracij lahko potrdijo resonančne pogoje.
Kakšna je razlika med prisilnimi vibracijami in resonanco?
Prisilno vibriranje se pojavi, kadar na sistem deluje zunanja sila, medtem ko je resonanca poseben pogoj, ko se frekvenca prisile ujema z lastno frekvenco sistema, kar povzroči okrepljen odziv. Vsaka resonanca vključuje vsiljene vibracije, vendar pa vse vsiljene vibracije ne povzročajo resonance.
Kako zasnova pnevmatskega cilindra brez palice vpliva na njegove vibracijske lastnosti?
Zasnova pnevmatskih cilindrov brez ročic s premikajočim se vozičkom, sistemom notranjega tesnjenja in vodilnimi mehanizmi ustvarja edinstvene izzive glede vibracij. Podaljšani profil deluje kot nosilec, ki se lahko upogiba, masa vozička ustvarja vztrajnostne sile, tesnilni trakovi pa lahko povzročajo spremenljivo trenje.
Katere preproste spremembe lahko zmanjšajo resonanco obstoječe opreme?
Pri obstoječi opremi, ki ima težave z resonanco, razmislite o dodajanju mase za spremembo lastne frekvence, namestitvi zunanjih blažilnikov ali amortizerjev, spremembi načinov montaže, da se zagotovi izolacija vibracij, ali prilagoditvi hitrosti delovanja, da se izognete resonančnim frekvencam.
-
Podaja temeljno razlago mehanske resonance, pogosto z vizualnimi primeri, ki prikazujejo, kako lahko majhna periodična sila v sistemu povzroči nihanja z veliko amplitudo. ↩
-
Ponuja podroben pregled fizike lastne frekvence, specifične frekvence, pri kateri sistem niha, če ni nobene gonilne ali dušilne sile. ↩
-
Razloži načela modela mase in vzmeti, temeljne idealizacije v fiziki in tehniki, ki se uporablja za analizo kompleksnih sistemov z enostavnim harmoničnim gibanjem. ↩
-
Podrobnosti Hookov zakon, fizikalno načelo, ki pravi, da je sila, potrebna za raztezanje ali stiskanje vzmeti za določeno razdaljo, neposredno sorazmerna s to razdaljo. ↩
-
Opisuje razmerje dušenja, brezrazsežno merilo, ki določa, kako se nihanja v sistemu zmanjšajo po motnji, kar je ključnega pomena za nadzor resonance. ↩


