Varje underhållsteknikers mardröm är oväntade fel på utrustningen. När maskiner vibrerar med sin naturliga frekvens kan katastrofala skador uppstå inom några minuter. Jag har sett hur detta problem kostar företag tusentals kronor i stilleståndstid.
Vibrationsresonans1 uppstår när en extern kraft matchar ett systems naturliga frekvens och orsakar förstärkta svängningar som kan skada utrustningen. Att förstå och kontrollera detta fenomen är viktigt för att förebygga fel och förlänga maskinernas livslängd.
Låt mig berätta en snabb historia. Förra året ringde en kund från Tyskland till mig i panik. Deras produktionslinje hade stannat på grund av en stånglös cylinder vibrerade våldsamt. Vad var problemet? Resonans. I slutet av den här artikeln kommer du att förstå hur du kan identifiera och förebygga liknande problem i dina system.
Innehållsförteckning
- Formel för naturlig frekvens: Hur kan du beräkna ditt systems sårbara punkter?
- Massfjädermodellen: Varför är detta förenklade tillvägagångssätt så värdefullt?
- Optimering av dämpningsförhållande: Vilka experiment ger bäst resultat?
- Slutsats
- Vanliga frågor om vibrationsresonans
Formel för naturlig frekvens: Hur kan du beräkna ditt systems sårbara punkter?
Att förstå din utrustnings egenfrekvens är det första steget mot att förebygga resonansproblem. Detta kritiska värde avgör när ditt system är som mest sårbart för vibrationsproblem.
Den naturlig frekvens2 (fn) för ett system kan beräknas med formeln: fn = (1/2π) × √(k/m), där k är styvhetskoefficienten och m är massan. Denna beräkning avslöjar den frekvens vid vilken ditt system kommer att resonera om det exciteras av matchande externa krafter.
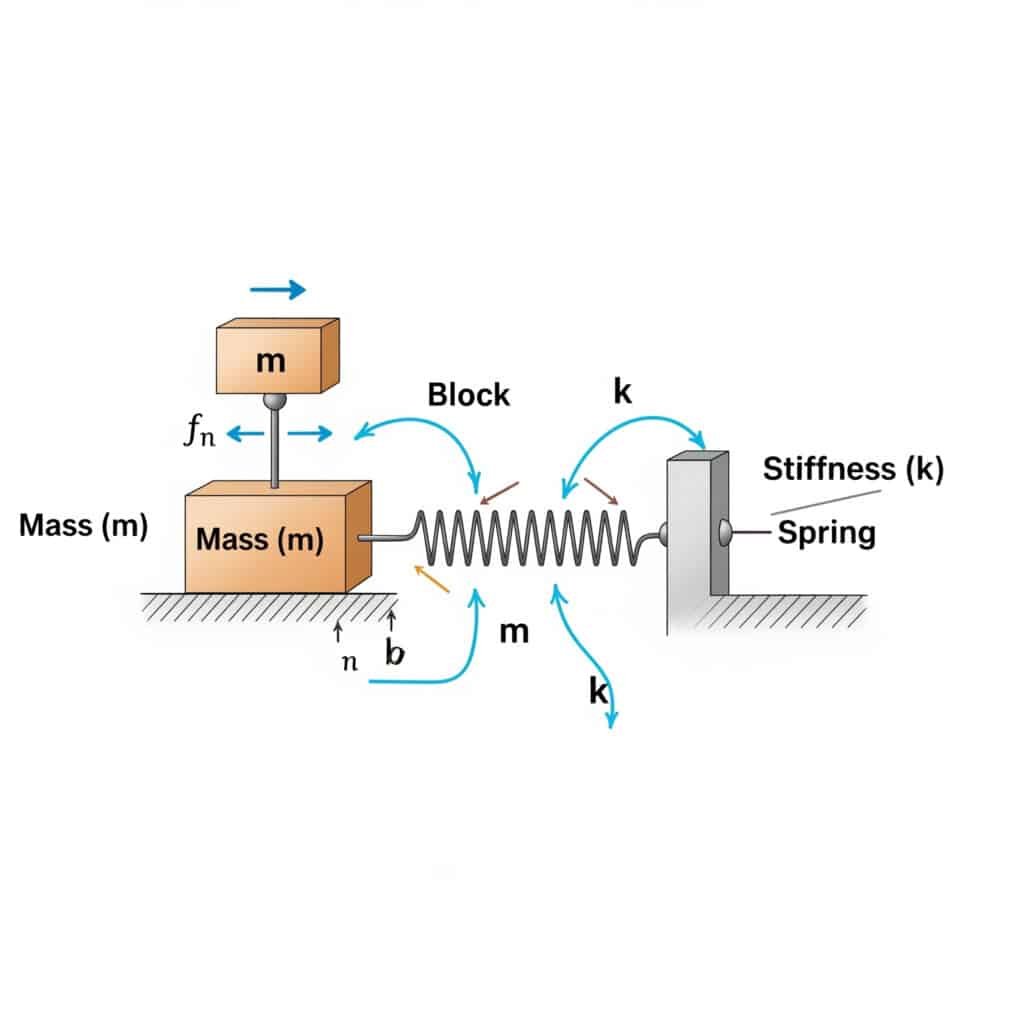
När jag besökte en tillverkningsanläggning i Schweiz upptäckte jag att deras stånglösa pneumatiska cylindrar gick sönder i förtid. Deras underhållsteam hade inte beräknat den naturliga frekvensen för deras installation. Efter att ha använt den här formeln kunde vi konstatera att deras drifthastighet låg farligt nära systemets egenfrekvens.
Praktiska tillämpningar av beräkningar av egenfrekvens
Formeln för egenfrekvens är inte bara teoretisk - den har direkta tillämpningar i olika industriella miljöer:
- Val av utrustning: Välja komponenter med egenfrekvenser som ligger långt från dina driftsförhållanden
- Förebyggande underhåll: Schemaläggning av inspektioner baserat på riskprofiler för vibrationer
- Felsökning: Identifiering av grundorsaken till oväntade vibrationer
Vanliga värden för egenfrekvens för industrikomponenter
| Komponent | Typiskt naturligt frekvensområde (Hz) |
|---|---|
| Stånglösa cylindrar | 10-50 Hz |
| Monteringsfästen | 20-100 Hz |
| Stödstrukturer | 5-30 Hz |
| Reglerventiler | 40-200 Hz |
Kritiska faktorer som påverkar egenfrekvensen
Beräkningen av egenfrekvensen verkar enkel, men flera faktorer kan komplicera tillämpningen i verkligheten:
- Icke-uniform massfördelning: De flesta industrikomponenter har inte perfekt fördelad massa
- Variabel styvhet: Komponenterna kan ha olika styvhet i olika riktningar
- Anslutningspunkter: Hur komponenter monteras påverkar avsevärt deras vibrationsegenskaper
- Temperaturpåverkan: Både mass- och styvhetsegenskaper kan förändras med temperaturen
Massfjädermodellen: Varför är detta förenklade tillvägagångssätt så värdefullt?
Massfjädermodellen ger ett intuitivt ramverk för att förstå komplexa vibrationssystem. Den reducerar komplicerade maskiner till grundläggande element som ingenjörer enkelt kan analysera.
Den massa-fjäder-modell3 förenklar vibrationsanalys genom att representera mekaniska system som diskreta massor som är förbundna med fjädrar. Detta tillvägagångssätt gör det möjligt för ingenjörer att förutsäga systemets beteende, identifiera potentiella resonansproblem och utveckla effektiva lösningar utan komplex matematik.
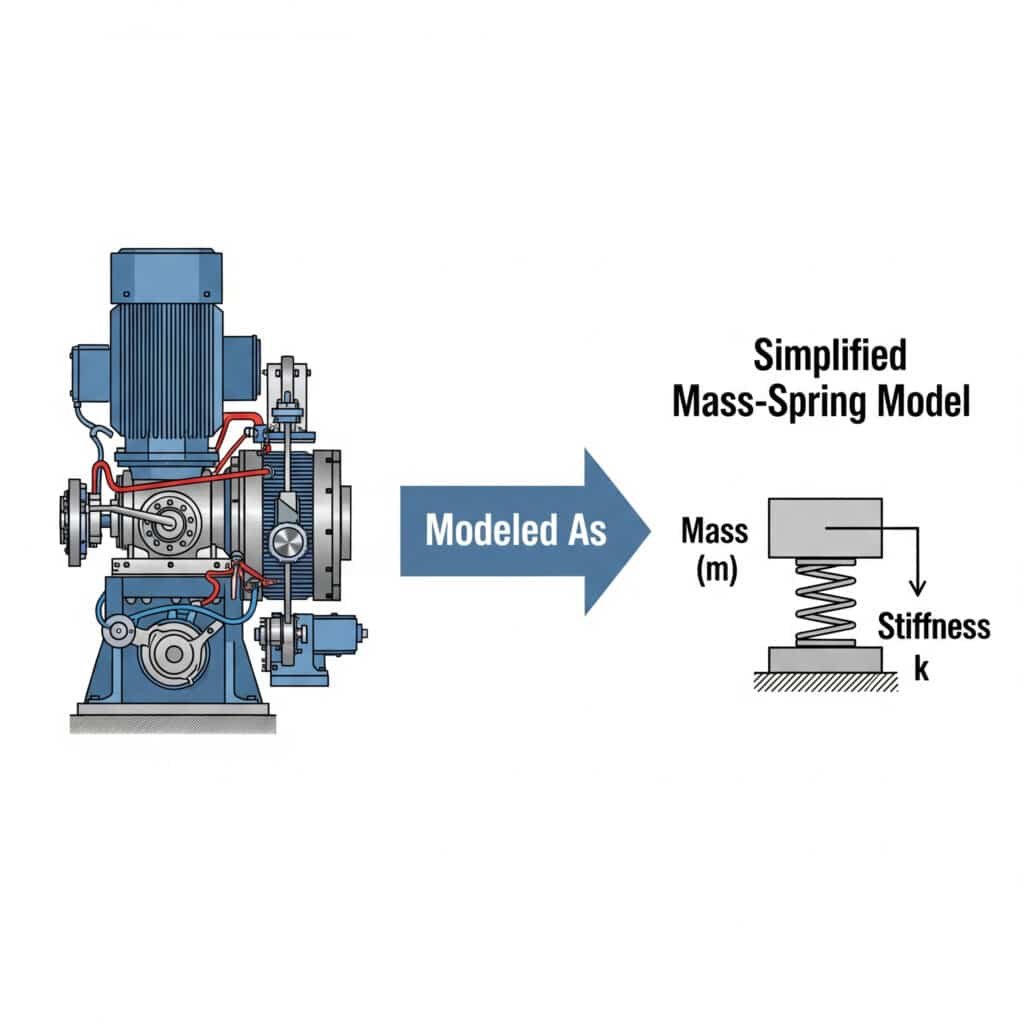
Jag minns att jag arbetade med en tillverkare av bildelar i Michigan som inte kunde förstå varför deras styrda stånglösa cylindrar inte fungerade. Genom att modellera deras system som ett enkelt massfjäderarrangemang identifierade vi att monteringsfästena fungerade som oavsiktliga fjädrar och skapade ett resonanstillstånd.
Konvertera verkliga system till modeller för massuttag
För att tillämpa detta tillvägagångssätt på din utrustning:
- Identifiera viktiga massor: Bestäm vilka komponenter som bidrar med betydande vikt
- Leta reda på fjäderelementen: Hitta komponenter som lagrar och avger energi (riktiga fjädrar, flexibla fästen etc.)
- Kartans anslutningar: Dokumentera hur massor och fjädrar samverkar
- Förenkla: Kombinera liknande element för att skapa en hanterbar modell
Olika typer av massfjädringssystem
| Typ av system | Beskrivning | Vanliga tillämpningar |
|---|---|---|
| Enkel DOF | En massa med en fjäder | Enkla pneumatiska cylindrar |
| Multi-DOF | Flera massor med flera fjädrar | Komplexa maskiner med flera komponenter |
| Kontinuerlig | Oändlig DOF (kräver annan analys) | Balkar, plattor och skal |
Överväganden om avancerad modellering
Även om den grundläggande massfjädermodellen är värdefull, finns det flera förbättringar som gör den mer realistisk:
- Lägga till dämpare: Verkliga system har alltid energiförluster
- Beaktande av olinjäriteter: Fjädrar följer inte alltid Hookes lag4 perfekt
- Redovisning av påtvingad vibration: Externa krafter förändrar systemets beteende
- Inklusive kopplingseffekter: Rörelse i en riktning kan påverka andra riktningar
Optimering av dämpningsförhållande: Vilka experiment ger bäst resultat?
Dämpning är det bästa försvaret mot resonansproblem. Att hitta det optimala dämpningsförhållandet genom experiment kan dramatiskt förbättra systemets prestanda och tillförlitlighet.
Dämpningsförhållande5 Optimeringsexperimenten innebär att man systematiskt testar olika dämpningskonfigurationer för att hitta den perfekta balansen mellan vibrationskontroll och systemets reaktionsförmåga. Det optimala dämpningsförhållandet ligger vanligtvis mellan 0,2 och 0,7, vilket ger tillräcklig vibrationsdämpning utan alltför stor energiförlust.
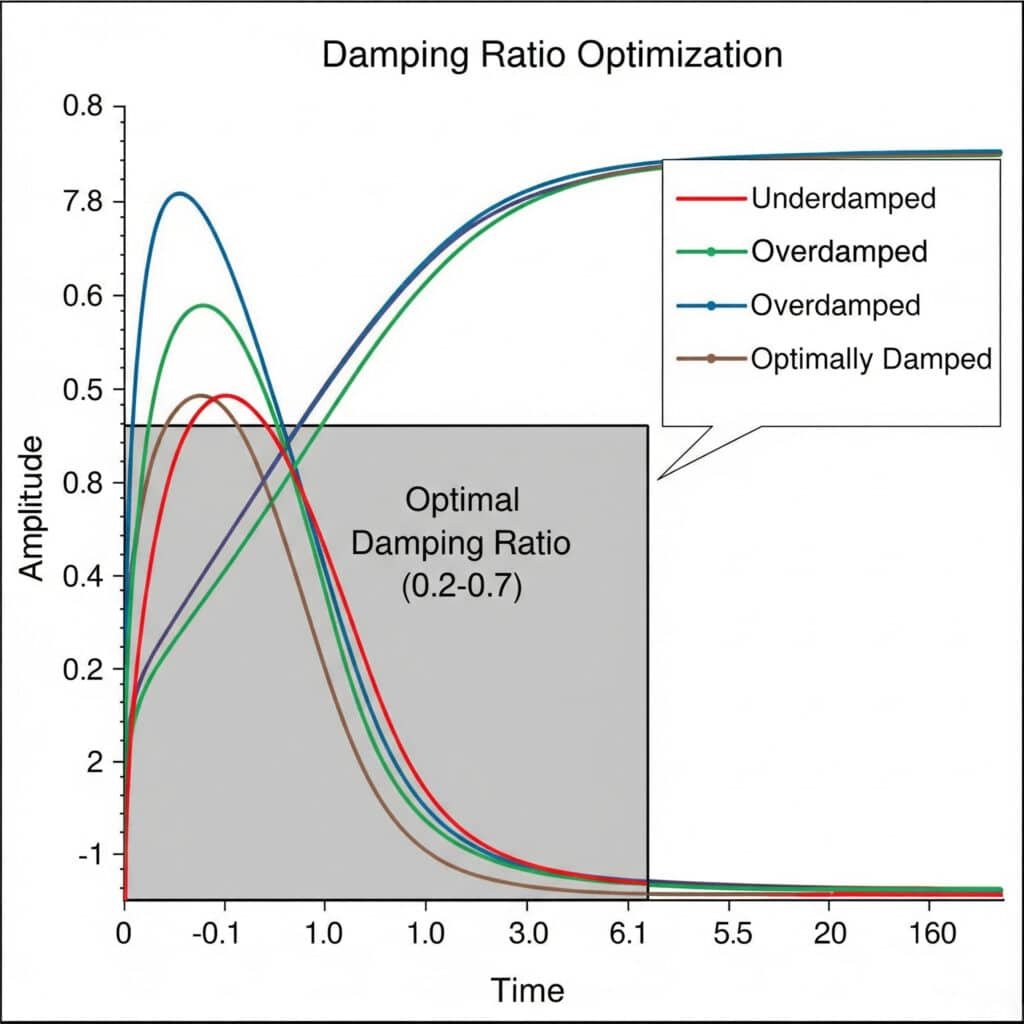
Förra månaden hjälpte jag en fransk tillverkare av utrustning för livsmedelsbearbetning att lösa ihållande vibrationsproblem i sina magnetiska stånglösa cylindrar. Genom en serie experiment med dämpningsförhållanden upptäckte vi att deras ursprungliga konstruktion hade ett dämpningsförhållande på endast 0,05 - alldeles för lågt för att förhindra resonansproblem.
Experimentell uppställning för test av dämpningsförhållande
För att genomföra effektiva experiment för optimering av dämpningen:
- Mätning vid baslinjen: Registrera systemets respons utan ytterligare dämpning
- Inkrementell testning: Lägg till dämpningselement i kontrollerade steg
- Mätning av svar: Mät amplitud, inställningstid och frekvenssvar
- Analys av data: Beräkna dämpningsförhållandet för varje konfiguration
- Validering: Verifiera prestanda under faktiska driftsförhållanden
Jämförelse av dämpningstekniker
| Dämpningsteknik | Fördelar | Begränsningar | Typiska tillämpningar |
|---|---|---|---|
| Viskösa dämpare | Förutsägbar prestanda, temperaturstabil | Kräver underhåll, potentiella läckor | Tunga maskiner, precisionsutrustning |
| Friktionsdämpare | Enkel design, kostnadseffektivt | Slitage över tid, olinjärt beteende | Strukturella stöd, basmaskineri |
| Material Dämpning | Inga rörliga delar, kompakt | Begränsat justeringsområde | Precisionsinstrument, vibrationsisolering |
| Aktiv dämpning | Anpassningsbar till förändrade förhållanden | Komplex, kräver ström | Kritiska applikationer, utrustning med variabelt varvtal |
Optimera dämpningen för olika driftsförhållanden
Det perfekta dämpningsförhållandet är inte universellt - det beror på din specifika applikation:
- Höghastighetsoperationer: Lägre dämpningsförhållanden (0,1-0,3) bibehåller responsen
- Precisionstillämpningar: Högre dämpningsförhållanden (0,5-0,7) ger stabilitet
- System med variabel belastning: Adaptiv dämpning kan vara nödvändig
- Temperaturkänsliga miljöer: Tänk på dämpningsmaterial med stabila egenskaper
Fallstudie: Optimering av dämpning i stånglösa cylindrar
När vi optimerade en dubbelverkande stånglös cylinder för en förpackningsmaskin testade vi fem olika dämpningskonfigurationer:
- Standard ändkuddar: Dämpningsförhållande = 0,12
- Förlängda kuddar: Dämpningsförhållande = 0,25
- Externa stötdämpare: Dämpningsförhållande = 0,41
- Monteringsfästen i komposit: Dämpningsförhållande = 0,38
- Kombinerat tillvägagångssätt (3+4): Dämpningsförhållande = 0,53
Det kombinerade tillvägagångssättet gav bäst resultat och minskade vibrationsamplituden med 78% samtidigt som svarstiderna var acceptabla.
Slutsats
Att förstå vibrationsresonans genom beräkningar av egenfrekvens, modellering av massa och fjädrar samt optimering av dämpningsförhållandet är avgörande för att förhindra fel på utrustningen. Genom att tillämpa dessa principer kan du förlänga maskinernas livslängd, minska stilleståndstiden och förbättra systemets övergripande prestanda.
Vanliga frågor om vibrationsresonans
Vad är vibrationsresonans i industriell utrustning?
Vibrationsresonans uppstår när en extern kraft matchar ett systems egenfrekvens och orsakar förstärkta svängningar. I industriell utrustning kan detta fenomen leda till överdriven rörelse, komponentutmattning och katastrofala fel om det inte hanteras på rätt sätt.
Hur kan jag identifiera om mitt system upplever resonans?
Leta efter symtom som oförklarliga bullerökningar, synliga vibrationer vid specifika hastigheter, förtida komponentfel och prestandaförsämring som inträffar vid konsekventa driftspunkter. Verktyg för vibrationsanalys kan bekräfta resonansförhållanden.
Vad är skillnaden mellan påtvingad vibration och resonans?
Påtvingad vibration uppstår när en extern kraft verkar på ett system, medan resonans är det specifika tillstånd när den påtvingade frekvensen matchar systemets egenfrekvens, vilket resulterar i förstärkt respons. All resonans innebär påtvingad vibration, men inte all påtvingad vibration orsakar resonans.
Hur påverkar konstruktionen av en stånglös pneumatisk cylinder dess vibrationsegenskaper?
Konstruktionen av stånglösa pneumatiska cylindrar - med sin rörliga vagn, interna tätningssystem och styrmekanismer - skapar unika vibrationsutmaningar. Den förlängda profilen fungerar som en balk som kan böjas, vagnens massa skapar tröghetskrafter och tätningsbanden kan ge upphov till varierande friktion.
Vilka enkla modifieringar kan minska resonansen i befintlig utrustning?
För befintlig utrustning som har problem med resonans kan man överväga att lägga till massa för att ändra den naturliga frekvensen, installera externa dämpare eller stötdämpare, ändra monteringsmetoderna så att de inkluderar vibrationsisolering eller justera drifthastigheterna för att undvika resonansfrekvenser.
-
Ger en grundläggande förklaring av mekanisk resonans, ofta med visuella exempel, som visar hur en liten periodisk kraft kan ge upphov till svängningar med stor amplitud i ett system. ↩
-
Ger en detaljerad inblick i fysiken bakom egenfrekvensen, den specifika frekvens vid vilken ett system tenderar att svänga i frånvaro av någon drivande eller dämpande kraft. ↩
-
Förklarar principerna för massfjädermodellen, en grundläggande idealisering inom fysik och teknik som används för att analysera komplexa system som uppvisar enkel harmonisk rörelse. ↩
-
Detaljer Hookes lag, en fysikalisk princip som säger att den kraft som krävs för att sträcka ut eller trycka ihop en fjäder ett visst avstånd är direkt proportionell mot detta avstånd. ↩
-
Beskriver dämpningsförhållandet, ett dimensionslöst mått som definierar hur svängningar i ett system avtar efter en störning, vilket är avgörande för att kontrollera resonans. ↩


