หลักการฟิสิกส์พื้นฐานใดที่ขับเคลื่อนประสิทธิภาพและประสิทธิผลของตัวกระตุ้นแบบใบพัด?

หลักฟิสิกส์ที่อยู่เบื้องหลังตัวกระตุ้นแบบใบพัดหมุนเกี่ยวข้องกับการปฏิสัมพันธ์ที่ซับซ้อนระหว่างพลศาสตร์ของไหล แรงกลไก และอุณหพลศาสตร์ ซึ่งวิศวกรส่วนใหญ่ไม่เคยเข้าใจอย่างถ่องแท้ อย่างไรก็ตาม การเชี่ยวชาญหลักการเหล่านี้มีความสำคัญอย่างยิ่งต่อการเพิ่มประสิทธิภาพ การทำนายพฤติกรรม และการแก้ไขปัญหาการประยุกต์ใช้ที่อาจทำให้โครงการประสบความสำเร็จหรือล้มเหลวได้ 🔬

ตัวกระตุ้นแบบโรตารีชนิดใบพัดทำงานตามหลักการของปาสกาลในการเพิ่มแรงดัน แปลงแรงอัดอากาศเชิงเส้นให้เป็นแรงบิดหมุนผ่านกลไกใบพัดที่เลื่อนไปมา โดยมีประสิทธิภาพที่ควบคุมโดยความแตกต่างของแรงดัน รูปทรงของใบพัด ค่าสัมประสิทธิ์แรงเสียดทาน และกฎทางอุณหพลศาสตร์ของแก๊สที่กำหนดแรงบิดที่ส่งออก ความเร็ว และลักษณะประสิทธิภาพ.

เมื่อไม่นานมานี้ ฉันได้ทำงานร่วมกับวิศวกรออกแบบชื่อเจนนิเฟอร์ที่โรงงานผลิตอากาศยานในเมืองซีแอตเทิล ซึ่งเธอกำลังประสบปัญหาความไม่สม่ำเสมอของแรงบิดในแอปพลิเคชันแอคชูเอเตอร์แบบหมุน แอคชูเอเตอร์ของเธอผลิตแรงบิดได้น้อยกว่าที่คำนวณไว้ถึง 30% ส่งผลให้เกิดข้อผิดพลาดในการกำหนดตำแหน่งในกระบวนการประกอบที่สำคัญ สาเหตุที่แท้จริงไม่ได้เกิดจากปัญหาทางกล แต่เป็นความเข้าใจผิดพื้นฐานเกี่ยวกับหลักฟิสิกส์ที่ควบคุมพฤติกรรมของแอคชูเอเตอร์แบบใบพัด ✈️

สารบัญ

• พลศาสตร์แรงดันสร้างแรงบิดหมุนในตัวกระตุ้นแบบใบพัดได้อย่างไร?
• รูปทรงของใบพัดมีบทบาทอย่างไรในการกำหนดลักษณะสมรรถนะของตัวกระตุ้น?
• หลักการทางอุณหพลศาสตร์ใดบ้างที่มีผลต่อความเร็วและประสิทธิภาพของแอคชูเอเตอร์แบบหมุน?
• แรงเสียดทานและการสูญเสียทางกลส่งผลต่อประสิทธิภาพของตัวกระตุ้นในโลกแห่งความเป็นจริงอย่างไร?

พลศาสตร์แรงดันสร้างแรงบิดหมุนในตัวกระตุ้นแบบใบพัดได้อย่างไร?

การเข้าใจการแปลงแรงดันเป็นแรงบิดเป็นพื้นฐานสำคัญสำหรับการออกแบบและการประยุกต์ใช้แอคชูเอเตอร์แบบหมุน.

ตัวกระตุ้นแบบใบพัดสร้างแรงบิดผ่านความแตกต่างของแรงดันที่กระทำต่อพื้นผิวใบพัด โดยที่แรงบิดเท่ากับผลคูณของความแตกต่างของแรงดันกับพื้นที่ใบพัดที่มีประสิทธิภาพ แขนแรง¹ ระยะทาง โดยมีความสัมพันธ์ T = ΔP × A × r ซึ่งถูกปรับแต่งด้วยมุมใบพัดและรูปทรงของห้องเพื่อสร้างการเคลื่อนที่แบบหมุนจากแรงลมเชิงเส้น.

หลักการพื้นฐานของการสร้างแรงบิด

หลักการของปาสกาล การประยุกต์ใช้

พื้นฐานของการทำงานของตัวกระตุ้นแบบหมุนอยู่ที่ หลักการของปาสกาล²:

• การส่งผ่านแรงดัน: แรงดันสม่ำเสมอออกแรงกระทำต่อทุกพื้นผิวภายในห้อง
• การเพิ่มกำลัง: แรงดัน × พื้นที่ = แรงกระทำต่อแต่ละผิวใบพัด  
• การสร้างช่วงเวลา แรง × รัศมี = แรงบิดรอบแกนกลาง

พื้นฐานการคำนวณแรงบิด

สูตรแรงบิดพื้นฐาน: T = ΔP × A_eff × r_eff × η

สถานที่:

• T = แรงบิดขาออก (ปอนด์-นิ้ว)
• ΔP = ความต่างของความดัน (PSI)
• A_eff = พื้นที่ใบพัดที่มีประสิทธิภาพ (ตารางนิ้ว)
• r_eff = แรงบิดมีผล (นิ้ว)
• η = ประสิทธิภาพทางกล (0.85-0.95)

การวิเคราะห์การกระจายแรงดัน

พลศาสตร์ความดันในห้องเผาไหม้

การกระจายความดันภายในห้องใบพัดไม่สม่ำเสมอ:

• ห้องความดันสูง: แรงดันจ่ายลบการสูญเสียการไหล
• ห้องความดันต่ำ: แรงดันไอเสียบวกกับแรงดันย้อนกลับ
• โซนเปลี่ยนผ่าน: ความชันของความดันที่ขอบใบพัด
• ปริมาณที่ตายแล้ว: อากาศที่ติดอยู่ในช่องว่าง

การคำนวณพื้นที่ที่มีผล

การจัดวางใบพัด	สูตรพื้นที่ที่มีประสิทธิภาพ	ปัจจัยประสิทธิภาพ
ใบพัดเดี่ยว	A = L × W × sin(θ)	0.85-0.90
ใบพัดคู่	A = 2 × L × W × sin(θ/2)	0.88-0.93
หลายใบพัด	A = n × L × W × sin(θ/n)	0.90-0.95

L = ความยาวของใบพัด, W = ความกว้างของใบพัด, θ = มุมการหมุน, n = จำนวนใบพัด

ผลกระทบของความดันแบบไดนามิก

การสูญเสียความดันที่เกิดจากการไหล

พลวัตของแรงกดดันในโลกแห่งความเป็นจริงรวมถึงการสูญเสียที่เกี่ยวข้องกับการไหล:

• ข้อจำกัดทางเข้า: การลดแรงดันของวาล์วและข้อต่อ
• การสูญเสียการไหลภายใน: ความปั่นป่วนและแรงเสียดทานในห้อง
• ข้อจำกัดการปล่อยไอเสีย: แรงดันย้อนกลับจากระบบไอเสีย
• การสูญเสียการเร่งความเร็ว: แรงดันที่ต้องการเพื่อเร่งความเร็วของอากาศที่เคลื่อนที่

แอปพลิเคชันด้านอวกาศของเจนนิเฟอร์ประสบปัญหาจากการกำหนดขนาดสายจ่ายที่ไม่เหมาะสม ซึ่งทำให้เกิดการลดลงของความดัน 15 PSI ระหว่างการเคลื่อนที่อย่างรวดเร็วของแอคชูเอเตอร์ การสูญเสียความดันนี้ เมื่อรวมกับผลกระทบจากการไหลแบบไดนามิก อธิบายถึงการลดลงของแรงบิด 30% ที่เธอประสบอยู่ 📉

รูปทรงของใบพัดมีบทบาทอย่างไรในการกำหนดลักษณะสมรรถนะของตัวกระตุ้น?

รูปทรงของใบพัดมีผลโดยตรงต่อแรงบิดที่ส่งออก มุมการหมุน ความเร็ว และลักษณะประสิทธิภาพ.

รูปทรงของใบพัดกำหนดประสิทธิภาพของตัวกระตุ้นผ่านความยาวของใบพัด (ส่งผลต่อแขนแรงบิด), ความกว้าง (กำหนดพื้นที่ความดัน), ความหนา (ส่งผลต่อการซีลและแรงเสียดทาน), ความสัมพันธ์ของมุม (ควบคุมช่วงการหมุน), และข้อกำหนดช่องว่าง (ส่งผลต่อการรั่วไหลและประสิทธิภาพ) โดยแต่ละพารามิเตอร์ต้องได้รับการปรับให้เหมาะสมสำหรับการใช้งานเฉพาะ.

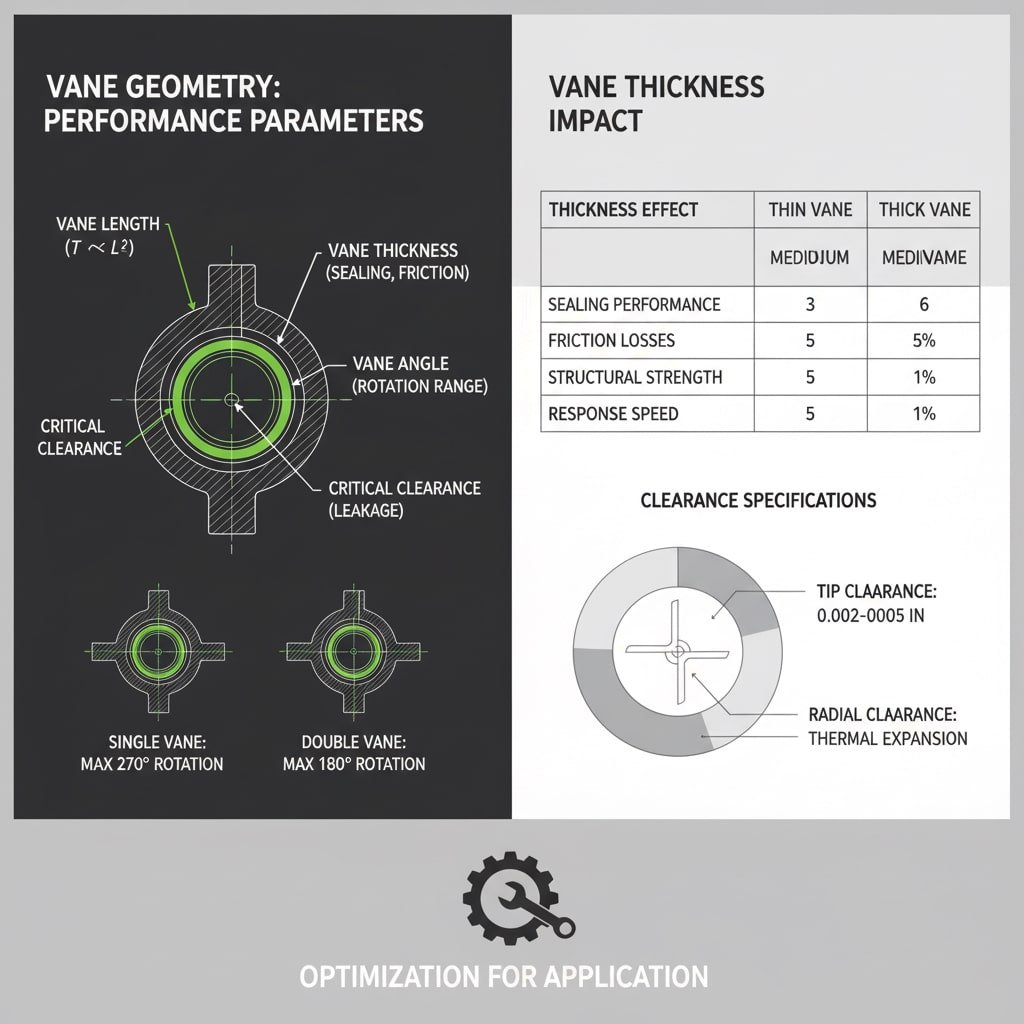
การวิเคราะห์พารามิเตอร์เชิงเรขาคณิต

การปรับความยาวใบพัดให้เหมาะสม

ความยาวของใบพัดส่งผลโดยตรงต่อแรงบิดที่ส่งออกและความสมบูรณ์ของโครงสร้าง:

• ความสัมพันธ์ของแรงบิด: T ∝ L² (ความสัมพันธ์ระหว่างความยาวยกกำลังสอง)
• ข้อควรพิจารณาเกี่ยวกับความเครียด: ความเค้นจากการดัดเพิ่มขึ้นตามความยาวยกกำลังสาม
• ผลกระทบจากการเบี่ยงเบน: ใบพัดที่ยาวขึ้นจะเกิดการเบี่ยงเบนของปลายมากขึ้น
• อัตราส่วนที่เหมาะสมที่สุด: อัตราส่วนความยาวต่อความกว้างตั้งแต่ 3:1 ถึง 5:1 ให้ประสิทธิภาพดีที่สุด

ผลกระทบของความหนาของใบพัด

ความหนาของใบพัดมีผลต่อพารามิเตอร์ประสิทธิภาพหลายประการ:

ผลกระทบของความหนา	ใบพัดบาง (< 0.25″)	ครีบขนาดกลาง (0.25 นิ้ว - 0.5 นิ้ว)	ใบพัดหนา (> 0.5″)
ประสิทธิภาพการปิดผนึก	แย่ - มีการรั่วไหลสูง	ดี – การติดต่อเพียงพอ	ยอดเยี่ยม – ซีลแน่นสนิท
การสูญเสียแรงเสียดทาน	ต่ำ	ระดับกลาง	สูง
ความแข็งแรงเชิงโครงสร้าง	แย่ - ปัญหาการเบี่ยงเบน	ดี – มีความแข็งเพียงพอ	ยอดเยี่ยม – แข็งแรง
ความเร็วในการตอบสนอง	รวดเร็ว	ระดับกลาง	ช้า

ข้อควรพิจารณาเกี่ยวกับเรขาคณิตเชิงมุม

ข้อจำกัดของมุมหมุน

รูปทรงของใบพัดจำกัดมุมการหมุนสูงสุด:

• ใบพัดเดี่ยว: หมุนได้สูงสุด ~270°
• ใบพัดคู่ หมุนได้สูงสุด ~180°  
• หลายใบพัด: การหมุนถูกจำกัดโดยการรบกวนของใบพัด
• การออกแบบห้อง: รูปทรงเรขาคณิตของที่อยู่อาศัยส่งผลต่อมุมที่สามารถใช้งานได้

การปรับมุมใบพัดให้เหมาะสม

มุมระหว่างใบพัดส่งผลต่อลักษณะของแรงบิด:

• ระยะห่างเท่ากัน: ให้แรงบิดที่ราบรื่น
• ระยะห่างไม่เท่ากัน: สามารถปรับเส้นโค้งแรงบิดให้เหมาะสมสำหรับการใช้งานเฉพาะได้
• มุมแบบก้าวหน้า: ชดเชยความแตกต่างของความดัน

เรขาคณิตของการเคลียร์และการปิดผนึก

ข้อกำหนดระยะห่างที่สำคัญ

ระยะห่างที่เหมาะสมช่วยสร้างสมดุลระหว่างประสิทธิภาพการปิดผนึกกับแรงเสียดทาน:

• ระยะห่างของปลายเครื่องมือ: 0.002″-0.005″ สำหรับการปิดผนึกที่ดีที่สุด
• ระยะห่างด้านข้าง: 0.001″-0.003″ เพื่อป้องกันการติดขัด
• ระยะห่างรัศมี: ข้อควรพิจารณาเกี่ยวกับการขยายตัวเนื่องจากอุณหภูมิ
• ระยะห่างแกน แบริ่งแรงขับและการขยายตัวจากความร้อน

ที่ Bepto กระบวนการเพิ่มประสิทธิภาพรูปทรงใบพัดของเราใช้ พลศาสตร์ของไหลเชิงคำนวณ (CFD)³ การวิเคราะห์ร่วมกับการทดสอบเชิงประจักษ์เพื่อให้ได้สมดุลที่เหมาะที่สุดของแรงบิด, ความเร็ว, และประสิทธิภาพสำหรับการใช้งานแต่ละอย่าง. แนวทางทางวิศวกรรมนี้ทำให้เราสามารถบรรลุประสิทธิภาพที่สูงขึ้นถึง 15-20% เมื่อเทียบกับการออกแบบมาตรฐาน. 🔧

หลักการทางอุณหพลศาสตร์ใดบ้างที่มีผลต่อความเร็วและประสิทธิภาพของแอคชูเอเตอร์แบบหมุน?

ผลกระทบทางเทอร์โมไดนามิกส์มีอิทธิพลอย่างมากต่อประสิทธิภาพของตัวกระตุ้น โดยเฉพาะอย่างยิ่งในกรณีการใช้งานที่มีความเร็วสูงหรือการใช้งานหนัก.

หลักการทางอุณหพลศาสตร์ที่มีผลต่อแอคชูเอเตอร์แบบหมุน ได้แก่ การขยายตัวและการบีบอัดของก๊าซระหว่างการหมุน การเกิดความร้อนจากแรงเสียดทานและการลดความดัน ผลกระทบของอุณหภูมิต่อความหนาแน่นและความหนืดของอากาศ และกระบวนการแบบไอโซบาริกเทียบกับไอโซเทอร์มอลที่กำหนดประสิทธิภาพจริงเทียบกับทฤษฎีในสภาวะการทำงานจริง.

การประยุกต์ใช้กฎของแก๊ส

ผลกระทบของกฎของแก๊สอุดมคติ

ประสิทธิภาพของตัวกระตุ้นแบบโรตารีเป็นไปตามความสัมพันธ์ของกฎของแก๊ส:

• งานปริมาตรความดัน: W = ∫P dV ระหว่างการขยายตัว
• ผลกระทบของอุณหภูมิ: PV = nRT ควบคุมความสัมพันธ์ระหว่างความดันและอุณหภูมิ
• การเปลี่ยนแปลงของความหนาแน่น: ρ = PM/RT มีผลต่อการคำนวณอัตราการไหลของมวล
• การบีบอัด: ผลกระทบของก๊าซจริงที่ความดันสูง

กระบวนการอะเดียแบติกเทียบกับกระบวนการไอโซเทอร์มอล

การทำงานของแอคชูเอเตอร์เกี่ยวข้องกับทั้งสองประเภทของกระบวนการ:

ประเภทของกระบวนการ	ลักษณะ	ผลกระทบต่อประสิทธิภาพ
อะเดียแบติก	ไม่มีการถ่ายเทความร้อน, การขยายตัวอย่างรวดเร็ว	แรงดันลดลงมากขึ้น, การเปลี่ยนแปลงของอุณหภูมิ
ไอโซเทอร์มอล	อุณหภูมิคงที่, การขยายตัวช้า	การแปลงพลังงานที่มีประสิทธิภาพมากขึ้น
โพลีโทรปิก	การผสมผสานในโลกจริง	ประสิทธิภาพจริงระหว่างค่าสูงสุดและต่ำสุด

การเกิดและการถ่ายเทความร้อน

การเกิดความร้อนจากการเสียดสี

แหล่งกำเนิดความร้อนหลายแหล่งในตัวกระตุ้นแบบหมุน:

• แรงเสียดทานปลายใบพัด: การสัมผัสแบบเลื่อนกับตัวเรือน
• แรงเสียดทานจากการหมุน: การสูญเสียของตลับลูกปืนรองรับเพลา
• แรงเสียดทานของซีล: แรงเสียดทานของซีลแบบหมุน
• แรงเสียดทานของของไหล: การสูญเสียความหนืดในกระแสอากาศ

การคำนวณการเพิ่มขึ้นของอุณหภูมิ

อัตราการเกิดความร้อน: Q = μ × N × F × V

สถานที่:

• Q = การผลิตความร้อน (BTU/ชั่วโมง)
• μ = ค่าสัมประสิทธิ์ความเสียดทาน
• N = ความเร็วรอบ (RPM)
• F = แรงปกติ (ปอนด์)
• V = ความเร็วในการเลื่อน (ฟุต/นาที)

การวิเคราะห์ประสิทธิภาพ

ปัจจัยประสิทธิภาพทางอุณหพลศาสตร์

ประสิทธิภาพโดยรวมรวมกลไกการสูญเสียหลายประการ:

• ประสิทธิภาพเชิงปริมาตร: ηv = อัตราการไหลจริง / อัตราการไหลตามทฤษฎี
• ประสิทธิภาพเชิงกล: ηm = กำลังไฟฟ้าขาออก / กำลังไฟฟ้าขาเข้า
• ประสิทธิภาพโดยรวม: ηo = ηv × ηm

กลยุทธ์การเพิ่มประสิทธิภาพ

กลยุทธ์	ประสิทธิภาพที่เพิ่มขึ้น	ค่าใช้จ่ายในการดำเนินการ
การปิดผนึกที่ดีขึ้น	5-15%	ระดับกลาง
ระยะห่างที่เหมาะสม	3-8%	ต่ำ
วัสดุขั้นสูง	8-12%	สูง
การจัดการความร้อน	5-10%	ระดับกลาง

พลศาสตร์ของไหลและการสูญเสียความดัน

ผลกระทบของตัวเลขเรย์โนลด์

ลักษณะการไหลเปลี่ยนแปลงตามเงื่อนไขการดำเนินงาน:

• การไหลแบบลามินาร์: Re < 2300, การสูญเสียแรงดันที่คาดการณ์ได้
• การไหลแบบปั่นป่วน: Re > 4000, ค่าสัมประสิทธิ์แรงเสียดทานสูงกว่า
• บริเวณเปลี่ยนผ่าน: ลักษณะการไหลที่ไม่สามารถคาดการณ์ได้

การวิเคราะห์ทางอุณหพลศาสตร์พบว่าแอปพลิเคชันด้านอวกาศของเจนนิเฟอร์มีการเพิ่มขึ้นของอุณหภูมิอย่างมีนัยสำคัญระหว่างการสลับการทำงานอย่างรวดเร็ว ซึ่งทำให้ความหนาแน่นของอากาศลดลง 12% และเป็นสาเหตุของการสูญเสียแรงบิด เราได้ดำเนินกลยุทธ์การจัดการความร้อนที่ช่วยฟื้นฟูประสิทธิภาพการทำงานเต็มรูปแบบ 🌡️

แรงเสียดทานและการสูญเสียทางกลส่งผลต่อประสิทธิภาพของตัวกระตุ้นในโลกแห่งความเป็นจริงอย่างไร?

แรงเสียดทานและการสูญเสียทางกลมีผลอย่างมากต่อการลดประสิทธิภาพทางทฤษฎี และจำเป็นต้องได้รับการจัดการอย่างรอบคอบเพื่อให้การทำงานของตัวกระตุ้นเป็นไปอย่างมีประสิทธิภาพสูงสุด.

การสูญเสียทางกลในตัวกระตุ้นแบบใบพัดประกอบด้วยแรงเสียดทานจากการเลื่อนที่ปลายใบพัด แรงเสียดทานจากซีลหมุน แรงเสียดทานจากตลับลูกปืน และความปั่นป่วนของอากาศภายใน ซึ่งโดยทั่วไปจะลดแรงบิดทางทฤษฎีลง 10-20% และจำเป็นต้องเลือกวัสดุอย่างระมัดระวัง ทำการปรับผิว และใช้กลยุทธ์การหล่อลื่นที่เหมาะสมเพื่อลดการเสื่อมประสิทธิภาพของตัวกระตุ้น.

การวิเคราะห์และจำลองแรงเสียดทาน

กลไกแรงเสียดทานปลายใบพัด

แหล่งเสียดทานหลักเกิดขึ้นที่บริเวณรอยต่อระหว่างใบพัดกับตัวเรือน:

• การหล่อลื่นบริเวณขอบเขต การสัมผัสโดยตรงระหว่างโลหะกับโลหะ
• การหล่อลื่นแบบผสม: การแยกชั้นของเหลวบางส่วน
• การหล่อลื่นแบบไฮโดรไดนามิก ฟิล์มของเหลวเต็มรูปแบบ (พบได้ยากในระบบนิวเมติกส์)

การเปลี่ยนแปลงของสัมประสิทธิ์แรงเสียดทาน

การผสมผสานวัสดุ	แรงเสียดทานแห้ง (μ)	แรงเสียดทานหล่อลื่น (μ)	ความไวต่ออุณหภูมิ
เหล็กปะทะเหล็ก	0.6-0.8	0.1-0.15	สูง
เหล็กบนทองสัมฤทธิ์	0.3-0.5	0.08-0.12	ระดับกลาง
เหล็กบน PTFE	0.1-0.2	0.05-0.08	ต่ำ
เคลือบเซรามิก	0.2-0.3	0.06-0.10	ต่ำมาก

การวิเคราะห์การสูญเสียการรับน้ำหนัก

แรงเสียดทานของแบริ่งรัศมี

แบริ่งเพลาขาออกมีส่วนทำให้เกิดการสูญเสียอย่างมีนัยสำคัญ:

• แรงเสียดทานกลิ้ง: Fr = μr × N × r
• แรงเสียดทานแบบเลื่อน Fs = μs × N
• แรงเสียดทานหนืด: เอฟวี = เอช × เอ × วี/เอช
• แรงเสียดทานของซีล: แรงต้านเพิ่มเติมจากซีลเพลา

ผลกระทบจากการเลือกแบริ่ง

ประเภทของแบริ่งที่แตกต่างกันส่งผลต่อประสิทธิภาพโดยรวม:

• ลูกปืนลูกกลิ้ง: แรงเสียดทานต่ำ ความแม่นยำสูง
• แบริ่งลูกกลิ้ง: ความสามารถในการรับน้ำหนักสูงขึ้น, แรงเสียดทานปานกลาง
• แบริ่งแบบเรียบ: แรงเสียดทานสูง โครงสร้างเรียบง่าย
• แบริ่งแม่เหล็ก: แรงเสียดทานเกือบเป็นศูนย์, ต้นทุนสูง

โซลูชันวิศวกรรมพื้นผิว

การบำบัดพื้นผิวขั้นสูง

การเคลือบผิวสมัยใหม่ช่วยลดแรงเสียดทานได้อย่างมาก:

• การชุบโครเมียมแข็ง: ลดการสึกหรอ ลดแรงเสียดทานในระดับปานกลาง
• เคลือบเซรามิก: ทนต่อการสึกหรอได้ดีเยี่ยม, แรงเสียดทานต่ำ
• คาร์บอนคล้ายเพชร (DLC): แรงเสียดทานต่ำมาก ราคาแพง
• โพลีเมอร์เฉพาะทาง: โซลูชันเฉพาะทางสำหรับแต่ละแอปพลิเคชัน

กลยุทธ์การหล่อลื่น

วิธีการหล่อลื่น	การลดแรงเสียดทาน	ข้อกำหนดการบำรุงรักษา	ผลกระทบต่อต้นทุน
ระบบกำจัดหมอกน้ำมัน	60-80%	สูง – เติมเต็มเป็นประจำ	สูง
สารหล่อลื่นชนิดแข็ง	40-60%	ต่ำ – อายุการใช้งานยาวนาน	ระดับกลาง
วัสดุหล่อลื่นตัวเอง	50-70%	ต่ำมาก – ถาวร	สูงในตอนแรก
สารหล่อลื่นฟิล์มแห้ง	30-50%	ระดับปานกลาง – การทบทวนหรือดำเนินการซ้ำเป็นระยะ	ต่ำ

กลยุทธ์การเพิ่มประสิทธิภาพการทำงาน

แนวทางการออกแบบแบบบูรณาการ

ที่ Bepto, เราเพิ่มประสิทธิภาพการเสียดสีผ่านการออกแบบอย่างเป็นระบบ:

• การเลือกวัสดุ: คู่ของวัสดุที่เข้ากันได้
• ผิวสำเร็จ: ปรับความหยาบให้เหมาะสมสำหรับแต่ละการใช้งาน
• การควบคุมการเคลียร์: ลดแรงกดสัมผัส
• การจัดการความร้อน: ควบคุมการขยายตัวที่เกิดจากอุณหภูมิ

การตรวจสอบประสิทธิภาพในโลกจริง

การทดสอบในห้องปฏิบัติการกับการทำงานในสนามมักจะแตกต่างกัน:

• ผลกระทบจากการเริ่มต้น: ประสิทธิภาพดีขึ้นเมื่อใช้งานครั้งแรก
• ผลกระทบจากการปนเปื้อน: ผลกระทบจากสิ่งสกปรกและเศษซากในชีวิตจริง
• การเปลี่ยนอุณหภูมิ: การขยายตัวและการหดตัวเนื่องจากความร้อน
• การเปลี่ยนแปลงของโหลด: การทดสอบแบบโหลดไดนามิกเปรียบเทียบกับเงื่อนไขการทดสอบแบบสถิต

โปรแกรมวิเคราะห์และเพิ่มประสิทธิภาพแรงเสียดทานอย่างครอบคลุมของเรา ช่วยให้แอปพลิเคชันด้านอวกาศของเจนนิเฟอร์สามารถสร้างแรงบิดทฤษฎีได้ถึง 95% ซึ่งเป็นการปรับปรุงที่สำคัญจากค่าเดิมที่ 70% กุญแจสำคัญคือการนำวิธีการแบบหลายมิติมาใช้ร่วมกัน ซึ่งรวมถึงวัสดุขั้นสูง รูปทรงที่ได้รับการปรับให้เหมาะสม และการหล่อลื่นที่เหมาะสม 🎯

การจำลองแรงเสียดทานเชิงคาดการณ์

แบบจำลองแรงเสียดทานทางคณิตศาสตร์

การคาดการณ์แรงเสียดทานอย่างแม่นยำต้องอาศัยการสร้างแบบจำลองที่ซับซ้อน:

• แรงเสียดทานคูลอมบ์: F = μ × N (แบบจำลองพื้นฐาน)
• เส้นโค้งสเตริบัก การเปลี่ยนแปลงของความเสียดทานตามความเร็ว
• ผลกระทบของอุณหภูมิ: ความสัมพันธ์ μ(T)
• การสวมใส่ตามลำดับ: แรงเสียดทานเปลี่ยนแปลงไปตามกาลเวลา

สรุป

การเข้าใจฟิสิกส์พื้นฐานของตัวกระตุ้นแบบใบพัดหมุน—ตั้งแต่พลศาสตร์ของแรงดันและอุณหพลศาสตร์ไปจนถึงกลไกการเสียดทาน—ช่วยให้วิศวกรสามารถเพิ่มประสิทธิภาพการทำงาน ทำนายพฤติกรรม และแก้ไขปัญหาการใช้งานที่ซับซ้อนได้.

คำถามที่พบบ่อยเกี่ยวกับฟิสิกส์ของแอคชูเอเตอร์แบบใบพัดหมุน

1. เรียนรู้ความหมายของแขนแรง ซึ่งเป็นระยะทางตั้งฉากจากแกนหมุนไปยังแนวกระทำของแรง ซึ่งมีความสำคัญอย่างยิ่งในการคำนวณแรงบิด. ↩

2. เข้าใจหลักการของปาสกาล ซึ่งเป็นกฎพื้นฐานของพลศาสตร์ของไหลที่อธิบายการถ่ายโอนความดันในของไหลที่ถูกกักขัง. ↩

3. สำรวจสาขาของพลศาสตร์ของไหลเชิงคำนวณ (CFD) ซึ่งเป็นสาขาหนึ่งของพลศาสตร์ของไหลที่ใช้การวิเคราะห์เชิงตัวเลขเพื่อแก้ปัญหาและวิเคราะห์ปัญหาที่เกี่ยวข้องกับการไหลของของไหล. ↩