Piston Kinematiği Pnömatik Sistem Performansınızı Nasıl Etkiler?

CQ2 Serisi Kompakt Pnömatik Silindir Montaj Kitleri

Tutarsız pnömatik silindir hızları veya beklenmedik strok sonu darbeleriyle mi mücadele ediyorsunuz? Bu yaygın sorunlar genellikle piston kinematiğinin yeterince anlaşılmamasından kaynaklanır. Birçok mühendis, sistem performansını belirleyen kritik hareket parametrelerini göz ardı ederek yalnızca kuvvet gereksinimlerine odaklanır.

Piston kinematiği¹ Basınç-hız ilişkileri, ivme limitleri ve yastıklama gereksinimleri aracılığıyla pnömatik sistem performansını doğrudan etkiler. Bu ilkelerin anlaşılması, mühendislerin bileşenleri uygun şekilde boyutlandırmasına, gerçek hareket profillerini tahmin etmesine ve kolsuz silindirlerde ve diğer pnömatik aktüatörlerde erken arızaları önlemesine olanak tanır.

Bepto'da pnömatik sistemlerle çalıştığım 15 yılı aşkın sürede, bu temel ilkeleri anlamanın müşterilerin kalıcı performans sorunlarını çözmesine ve ekipman ömrünü 3-5 kat uzatmasına yardımcı olduğu sayısız vaka gördüm.

İçindekiler

Sabit Hızda Hareket İçin Gerçekte Hangi Basınca İhtiyacınız Var?
Pnömatik Silindirlerde Olası Maksimum İvmeyi Nasıl Hesaplarsınız?
Yastıklama Süresi Neden Önemlidir ve Nasıl Hesaplanır?
Sonuç
Pnömatik Sistemlerde Piston Kinematiği Hakkında SSS

Sabit Hızda Hareket İçin Gerçekte Hangi Basınca İhtiyacınız Var?

Birçok mühendis pnömatik sistemlerine sadece mevcut maksimum basıncı uygular, ancak bu yaklaşım verimsizdir ve sarsıntılı harekete, aşırı aşınmaya ve boşa harcanan enerjiye yol açabilir.

Bir pnömatik silindirde sabit hızda hareket için gereken basınç P = (F + Fr)/A kullanılarak hesaplanır; burada P basınç, F harici yük kuvveti, Fr sürtünme direnci ve A piston alanıdır. Bu hesaplama, enerjiyi boşa harcayan ve bileşen aşınmasını hızlandıran aşırı basınç olmadan sorunsuz ve verimli çalışma sağlar.

Pnömatik bir silindir için basınç hesaplamasını açıklayan teknik bir serbest gövde diyagramı. 'Dış Yük (F)' olarak etiketlenmiş bir bloğu iten bir silindirin kesitini göstermektedir. Bir ok, karşıt 'Sürtünmeyi (Fr)' göstermektedir. İçerideki basınç 'P' olarak etiketlenmiştir ve 'Piston Alanı (A)' üzerine etki eder. 'P = (F + Fr)/A' formülü, her değişkeni diyagramdaki karşılık gelen kuvvet veya özelliğe bağlayan oklarla belirgin bir şekilde gösterilir. — Sabit hızlı basınç hesaplama diyagramı

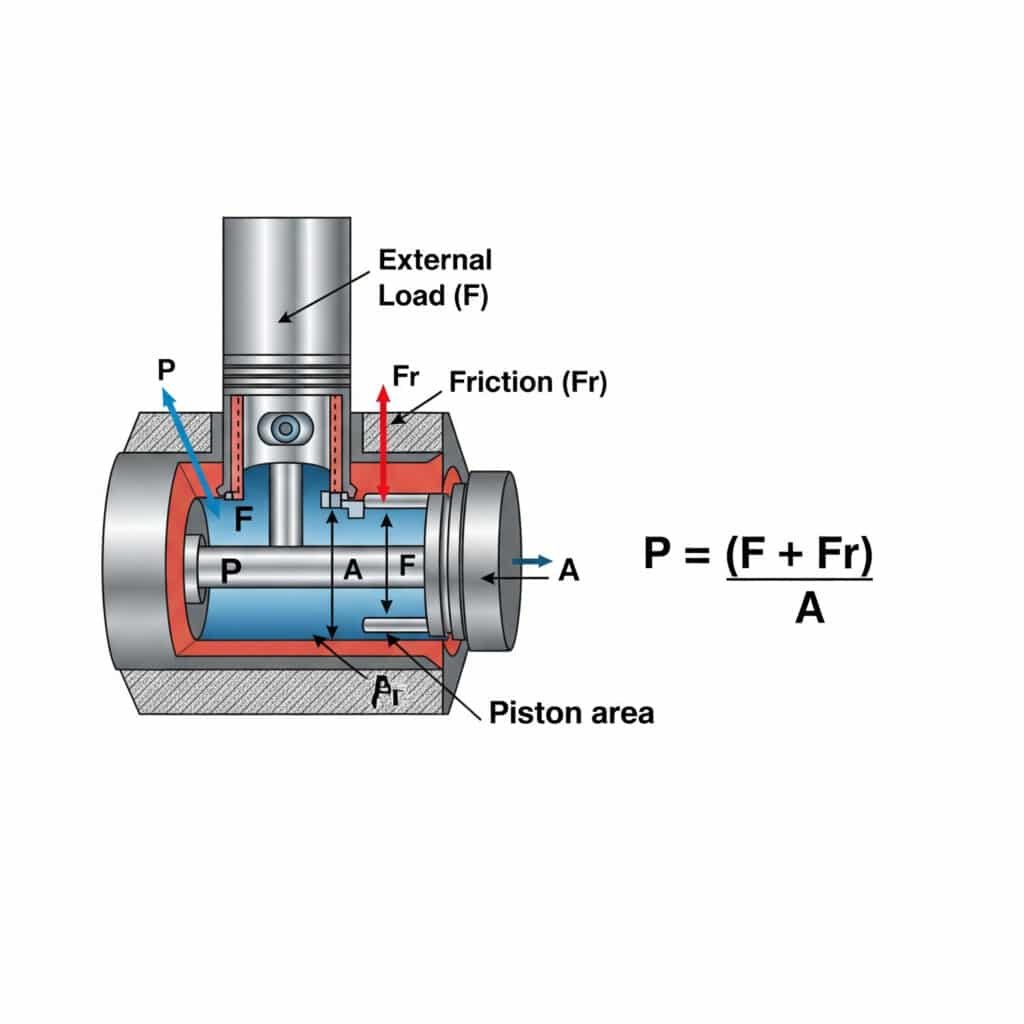
Sabit hızlı hareket için basınç gereksinimlerinin anlaşılması, sistem tasarımı ve işletimi için pratik sonuçlar doğurur. Bunu uygulanabilir içgörülere ayırmama izin verin.

Sabit Hız için Basınç Gereksinimlerini Etkileyen Faktörler

Sabit hızı korumak için gereken basınç çeşitli faktörlere bağlıdır:

Faktör	Basınç Gereksinimi Üzerindeki Etkisi	Pratik Değerlendirme
Harici Yük	Doğrudan doğrusal ilişki	Oryantasyon ve dış güçlere göre değişir
Sürtünme	Gerekli basınca katkıda bulunur	Conta aşınması ve yağlama ile ilgili değişiklikler
Piston Alanı	Ters orantılı	Daha büyük delik = daha düşük basınç gereksinimi
Hava Kaynağı Kısıtlamaları	Hatlarda/valflerde basınç düşüşleri	Minimum basınç düşüşü için bileşenleri boyutlandırın
Geri Basınç	Önergeye karşı çıkıyor	Egzoz akış kapasitesini göz önünde bulundurun

Kararlı Hareket için Minimum Basıncın Hesaplanması

Kararlı hareket için gereken minimum basıncı belirlemek:

Dış yükün üstesinden gelmek için gereken kuvveti hesaplayın
Sürtünme kuvvetini ekleyin (tipik olarak maksimum kuvvetin 3-20%'si)
Etkin piston alanına bölün
Bir kararlılık faktörü ekleyin (tipik olarak 10-30%)

Örneğin, 10 kg yük ve 15% sürtünme ile 40 mm delikli rotsuz bir silindirde:

Parametre	Hesaplama	Sonuç
Yük Kuvveti	10kg × 9.81m/s²	98.1N
Sürtünme Kuvveti	6 bar'da 15% maksimum kuvvet	~45N
Toplam Güç	98.1N + 45N	143.1N
Piston Alanı	π × (0,02m)²	0.00126m²
Minimum Basınç	143.1N ÷ 0.00126m²	113.571 Pa (1,14 bar)
20% Stabilite Faktörü ile	1,14 bar × 1,2	1.37 bar

Gerçek Dünya Uygulaması: Basınç Optimizasyonu ile Enerji Tasarrufu

Geçen yıl Michigan'da bir mobilya üretim tesisinde üretim mühendisi olan Robert ile birlikte çalıştım. Otomatik montaj hattında, yükten bağımsız olarak tam 6 bar besleme basıncında çalışan çubuksuz silindirler kullanılıyordu.

Uygulamasını analiz ettikten sonra, çoğu hareketin kararlı çalışma için yalnızca 2,5-3 bar gerektirdiğini belirledik. Yükleyerek oransal basinç regülatörleri̇aynı döngü süresini korurken hava tüketimini 40% azalttık. Bu sayede enerji maliyetlerinde yılda yaklaşık $12.000 tasarruf sağlanırken conta aşınması azaltıldı ve bakım aralıkları uzatıldı.

Gerçek Sistemlerde Hız-Basınç İlişkisi

Pratikte, basınç ve hız arasındaki ilişki, aşağıdaki nedenlerden dolayı mükemmel doğrusal değildir:

Akış kısıtlamaları: Valf ve port boyutlandırması ulaşılabilecek maksimum hızı etkiler
Sıkıştırılabilirlik etkileri: Hava sıkıştırılabilir, hızlanma gecikmelerine neden olur
Çubuk-kayma fenomeni: Sürtünme özellikleri hız ile değişir
Atalet etkileri: Kütle ivmesi ek kuvvet/basınç gerektirir

Pnömatik Silindirlerde Olası Maksimum İvmeyi Nasıl Hesaplarsınız?

İvme limitlerini anlamak, pnömatik sistemlerde aşırı şok, titreşim ve erken bileşen arızasını önlemek için çok önemlidir.

Bir pnömatik silindirde mümkün olan maksimum hızlanma a = (P × A - F - Fr)/m kullanılarak hesaplanır; burada a hızlanma, P basınç, A piston alanı, F harici yük, Fr sürtünme direnci ve m hareketli kütledir. Bu denklem, bir pnömatik aktüatörün hareketi ne kadar hızlı başlatabileceği veya durdurabileceğinin fiziksel sınırlarını tanımlar.

Pnömatik silindir ivmesinin hesaplanmasını açıklayan teknik bir serbest cisim diyagramı. Resimde 'Hareketli Kütle (m)' olarak etiketlenmiş bir bloğu iten bir silindir gösterilmektedir. Büyük bir ok, 'Piston Alanı (A)' üzerindeki 'Basınç (P)' tarafından oluşturulan itici kuvveti göstermektedir. Bunun karşısında 'Dış Yük (F)' ve 'Sürtünme (Fr)' olarak etiketlenmiş iki küçük ok bulunmaktadır. Büyük bir ok ortaya çıkan 'İvmeyi (a)' gösterir. 'a = (P × A - F - Fr)/m' formülü belirgin bir şekilde gösterilir ve her değişken diyagramdaki karşılık gelen öğeye bağlanır. — İvme limiti türetme diyagramı

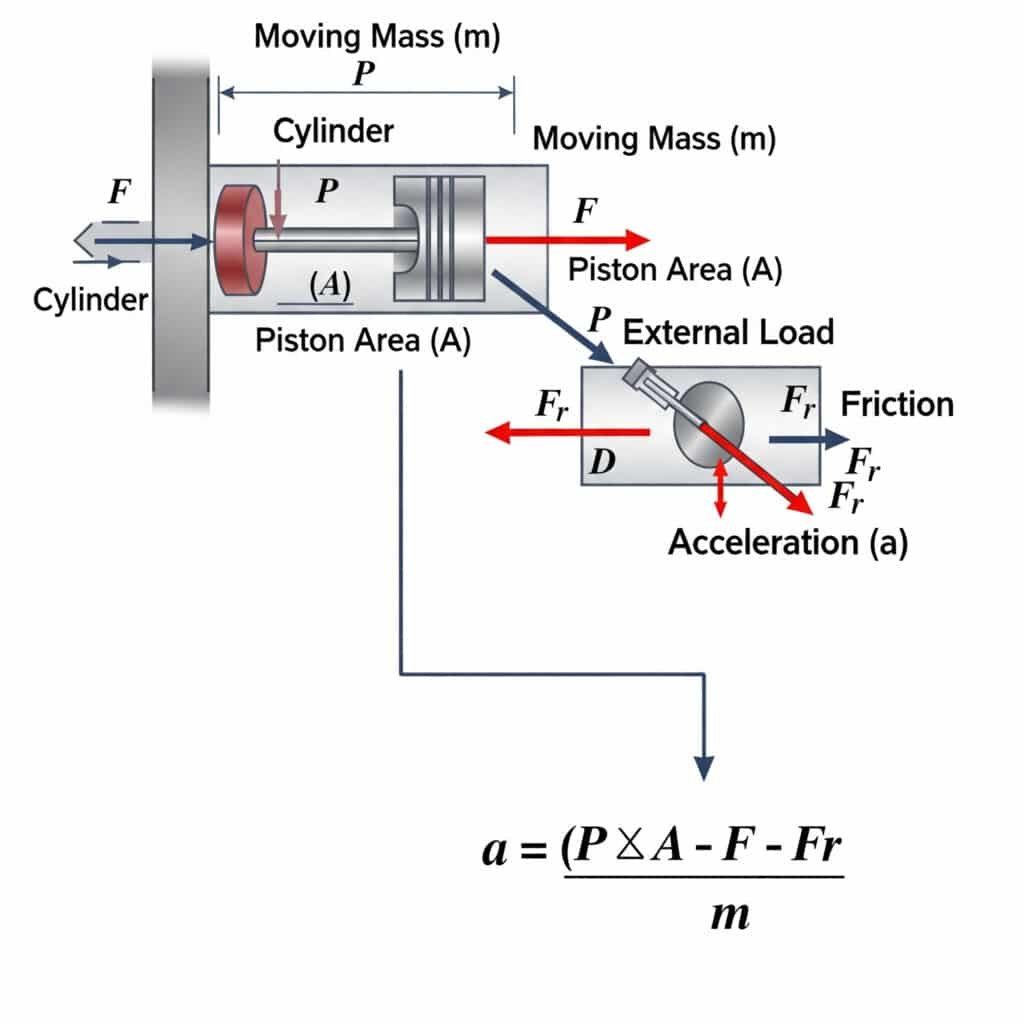
Teorik hızlanma limitleri, sistem tasarımı ve bileşen seçimi için önemli pratik sonuçlara sahiptir.

İvme Sınır Denkleminin Türetilmesi

İvme sınırı denklemi şuradan gelir Newton'un İkinci Yasası² (F = ma):

İvme için mevcut net kuvvet şudur: Fnet = Fbasınç - Fyük - Fsürtünme
Fbasınç = P × A
Bu nedenle: a = Fnet/m = (P × A - F - Fr)/m

Farklı Silindir Tipleri için Pratik İvme Sınırları

Farklı silindir tasarımlarının farklı pratik hızlanma limitleri vardır:

Silindir Tipi	Tipik Maksimum İvme	Sınırlayıcı Faktörler
Standart çubuk silindir	10-15 m/s²	Çubuk burkulması, yatak yükleri
Çubuksuz silindir (manyetik)	8-12 m/s²	Manyetik bağlantı gücü
Rotsuz silindir (mekanik)	15-25 m/s²	Conta/yatak tasarımı, iç sürtünme
Kılavuz silindir	20-30 m/s²	Kılavuz sistemi sertliği, taşıma kapasitesi
Darbe silindiri	50-100+ m/s²	Yüksek hızlanma için özel olarak tasarlanmıştır

İvme Hesaplamalarında Kütlenin Dikkate Alınması

İvmeyi hesaplarken, hareket eden tüm kütleleri dahil etmek çok önemlidir:

Piston tertibatı: Piston, contalar ve bağlantı elemanlarını içerir
Yük kütlesi: Taşınan harici yük
Hareket eden havanın etkin kütlesi: Genellikle ihmal edilebilir ancak yüksek hızlı uygulamalarda önemlidir
Montaj bileşenleri nedeniyle eklenen kütle: Braketler, sensörler, vb.

Bir keresinde Fransa'da çubuksuz silindir sisteminde gizemli arızalar yaşayan bir müşterime yardımcı olmuştum. Silindir, belirtilen 15 kg yük için doğru şekilde boyutlandırılmıştı, ancak birkaç bin döngüden sonra sürekli olarak arızalanıyordu.

Araştırmanın ardından, montaj plakası ve ek parçalarının 12 kg'lık kütlesini hesaba katmayı ihmal ettiğini keşfettik. Gerçek hareketli kütle, hesapladığının neredeyse iki katıydı ve silindirin tasarım sınırlarını aşan ivmelenme kuvvetlerine neden oldu. Daha büyük bir silindire geçtikten sonra arızalar tamamen durdu.

İvme Kontrol Yöntemleri

İvmeyi güvenli sınırlar içinde kontrol etmek için:

Akış kontrol valfleri: İlk hareket sırasında akış hızını sınırlayın
Oransal valfler: Kontrollü basınç artışı sağlayın
Çok aşamalı hızlanma: Kademeli basınç artışlarını kullanın
Mekanik sönümleme: Harici amortisörler ekleyin
Elektronik kontrol: Kullanım servo-pnömati̇k si̇stemler³ hızlanma geri bildirimi ile

Yastıklama Süresi Neden Önemlidir ve Nasıl Hesaplanır?

Uygun strok sonu yastıklama, darbe hasarını önlemek, gürültüyü azaltmak ve pnömatik silindirlerin ömrünü uzatmak için gereklidir. Yastıklama süresinin anlaşılması, mühendislerin döngü süresini bileşen ömrüyle dengeleyen sistemler tasarlamasına yardımcı olur.

Pnömatik silindirlerde yastıklama süresi t = √(2s/a) denklemi kullanılarak hesaplanır; burada t zaman, s yastıklama stroku uzunluğu ve a yavaşlamadır. Bu süre, silindirin ve bağlı bileşenlerin hasar görmesini önlemek için kritik öneme sahip olan çarpmadan önce hareketli kütleyi güvenli bir şekilde yavaşlatmak için gereken süreyi temsil eder.

Pnömatik yastıklama süresinin hesaplanmasını açıklayan teknik bir infografik. Bir silindirin sonunda yastığa giren bir pistonun büyütülmüş bir kesitini göstermektedir. Bir boyut çizgisi 'Yastıklama Strokunu (s)' gösterirken, büyük bir karşıt ok 'Yavaşlamayı (a)' temsil eder. Bir kronometre simgesi 'Yastıklama Süresini (t)' görselleştirir. 't = √(2s/a)' formülü, her değişkeni diyagramdaki karşılık gelen öğeye bağlayan oklarla birlikte belirgin bir şekilde görüntülenir. — İvme limiti türetme diyagramı

Şimdi yastıklama süresi hesaplamalarının pratik yönlerini ve bunların sistem tasarımı üzerindeki etkilerini inceleyelim.

Pnömatik Yastıklamanın Arkasındaki Fizik

Pnömatik yastıklama kontrollü hava sıkıştırma ve kısıtlı egzoz yoluyla çalışır:

Piston yastık odasına girdiğinde egzoz yolu kısıtlanır
Sıkışan hava sıkışarak artan bir geri basınç oluşturur
Bu geri basınç, pistonu yavaşlatan bir karşı kuvvet oluşturur
Yavaşlama profili yastık tasarımına ve ayarına bağlıdır

Optimum Yastıklama Süresinin Hesaplanması

Optimum yastıklama süresi, darbe önleme ile döngü süresi verimliliğini dengeler:

Parametre	Formül	Örnek
Yastıklama Mesafesi	Silindir tasarımına göre	15 mm (40 mm delik için tipik)
Gerekli Yavaşlama	a = v²/(2s)	v=0,5m/s, s=15mm için: a = 8,33m/s²
Yastıklama Süresi	t = √(2s/a)	t = √(2×0.015/8.33) = 0.06s
Basınç Oluşumu	P = P₀(V₀/V)^γ	Yastık odası geometrisine bağlıdır

Yastıklama Performansını Etkileyen Faktörler

Gerçek yastıklama performansını etkileyen çeşitli faktörler vardır:

Yastık conta tasarımı: Yastıklama sırasında hava sızıntısını etkiler
İğne valfi ayarı: Egzoz kısıtlama oranını kontrol eder
Hareketli kütle: Daha ağır yükler daha uzun yastıklama süresi gerektirir
Yaklaşım hızı: Daha yüksek hızlar daha uzun yastık mesafesi gerektirir
Çalışma basıncı: Mevcut maksimum karşı kuvveti etkiler

Yastıklama Türleri ve Uygulamaları

Farklı uygulamalar için farklı yastıklama mekanizmaları uygundur:

Yastıklama Tipi	Özellikler	En İyi Uygulamalar
Sabit yastıklama	Basit, ayarlanamaz	Hafif yükler, tutarlı çalışma
Ayarlanabilir yastıklama	İğne valfler ile ayarlanabilir	Değişken yükler, esnek uygulamalar
Kendinden ayarlı yastıklama	Farklı koşullara uyum sağlar	Değişen hızlar ve yükler
Harici amortisörler	Yüksek enerji emilimi	Ağır yükler, yüksek hızlar
Elektronik yastıklama	Hassas kontrollü yavaşlama	Servo-pnömatik sistemler

Örnek Olay İncelemesi: Yüksek Döngülü Uygulamalarda Yastıklamanın Optimize Edilmesi

Kısa bir süre önce Almanya'da bir otomotiv parçaları üreticisinde tasarım mühendisi olan Thomas ile çalıştım. Montaj hattında dakikada 45 devirle çalışan kolsuz silindirler kullanılıyordu, ancak sık sık conta arızaları ve montaj braketi hasarları yaşanıyordu.

Analiz, yastıklama süresinin hareketli kütle için çok kısa olduğunu ve strokun her sonunda yaklaşık 3G'lik darbe kuvvetlerine neden olduğunu ortaya koydu. Yastıklama strokunu 12 mm'den 20 mm'ye çıkararak ve iğne valfi ayarlarını optimize ederek yastıklama süresini 0,04 saniyeden 0,07 saniyeye uzattık.

Bu küçük gibi görünen değişiklik, darbe kuvvetlerini 60%'nin üzerinde azalttı, braket hasarını tamamen ortadan kaldırdı ve conta ömrünü 3 aydan bir yılın üzerine çıkardı; tüm bunları yaparken gerekli döngü süresini de korudu.

Pratik Yastıklama Ayarlama Prosedürü

Rotsuz silindirlerde optimum yastıklama performansı için:

Yastık valfleri tamamen açık olarak başlayın (minimum kısıtlama)
Yumuşak yavaşlama elde edilene kadar yastık valfini kademeli olarak kapatın
Beklenen minimum ve maksimum yüklerle test edin
Tüm hız aralığında yastıklama performansını doğrulayın
Yetersiz yastıklamaya işaret eden darbe seslerini dinleyin
Hesaplamaları doğrulamak için gerçek yavaşlama süresini ölçün

Sonuç

Sabit hız için basınç gereksinimlerinden hızlanma limitlerine ve yastıklama süresi hesaplamalarına kadar piston kinematiği ilkelerini anlamak, verimli ve güvenilir pnömatik sistemler tasarlamak için çok önemlidir. Bu ilkeleri kolsuz silindir uygulamalarınıza uygulayarak performansı optimize edebilir, enerji tüketimini azaltabilir ve bileşen ömrünü önemli ölçüde uzatabilirsiniz.

Pnömatik Sistemlerde Piston Kinematiği Hakkında SSS

Belirli bir silindir hızı için hangi basınca ihtiyacım var?

Gereken basınç yüke, sürtünmeye ve silindir alanına bağlıdır. P = (F + Fr)/A kullanarak hesaplayın; burada F harici yük kuvveti, Fr sürtünme direnci ve A piston alanıdır. Yatay olarak 10 kg'lık bir yükü hareket ettiren tipik bir kolsuz silindir için, orta hızlarda kararlı hareket için yaklaşık 1,5-2 bar'a ihtiyacınız olacaktır.

Bir pnömatik silindir ne kadar hızlanabilir?

Bir pnömatik silindirin maksimum ivmesi a = (P × A - F - Fr)/m kullanılarak hesaplanır. Tipik rotsuz silindirler tasarıma bağlı olarak 10-25 m/s² ivme elde edebilir. Bu, optimum koşullar altında yaklaşık 20-50 milisaniyede 0,5 m/s hıza ulaşmak anlamına gelir.

Rotsuz bir silindirin maksimum hızını sınırlayan faktörler nelerdir?

Maksimum hız, valf akış kapasitesi, hava besleme hacmi, port boyutlandırması, yastıklama yetenekleri ve conta tasarımı ile sınırlıdır. Çoğu standart rotsuz silindir 0,8-1,5 m/s maksimum hızlar için tasarlanmıştır, ancak özel yüksek hızlı tasarımlar 2-3 m/s'ye ulaşabilir.

Uygulamam için uygun yastıklamayı nasıl hesaplayabilirim?

Hareketli yükünüzün kinetik enerjisini (KE = ½mv²) belirleyerek ve yastıklama sisteminizin bu enerjiyi absorbe edebildiğinden emin olarak uygun yastıklamayı hesaplayın. Yastıklama süresi t = √(2s/a) kullanılarak hesaplanmalıdır; burada s yastıklama mesafesi ve a istenen yavaşlama oranıdır.

Pnömatik silindirim çok hızlı hızlanırsa ne olur?

Aşırı hızlanma, montaj bileşenleri üzerinde mekanik gerilime, erken conta aşınmasına, titreşim ve gürültünün artmasına, potansiyel yük kaymasına veya hasara ve sistem hassasiyetinin azalmasına neden olabilir. Ayrıca hassas uygulamalarda ürün kalitesini etkileyen sarsıntılı hareketlere de yol açabilir.

Yükün yönelimi hareket için gereken basıncı nasıl etkiler?

Yük yönü basınç gereksinimlerini önemli ölçüde etkiler. Yerçekimine karşı hareket eden dikey yükler, yerçekimi kuvvetinin üstesinden gelmek için ek basınç gerektirir (P = F/A + Fg/A + Fr/A). Yatay yüklerin yalnızca sürtünme ve ataletin üstesinden gelmesi gerekir. Eğimli yükler, açının sinüsüne bağlı olarak bu uç noktalar arasında yer alır.

Harekete neden olan kuvvetleri dikkate almadan nesnelerin hareketini tanımlayan mekanik dalı olan kinematiğin temel bir açıklamasını sağlar.
elektronik giriş sinyali, gelişmiş pnömatik kontrol sağlar. ↩
Newton'un İkinci Yasasını (F=ma), bir nesneye etki eden kuvveti kütlesi ve ivmesi ile ilişkilendiren ve tüm dinamik hesaplamaların temelini oluşturan fiziğin temel ilkesini detaylandırır. ↩
Yüksek doğrulukta konumlandırma ve hareket profilleri elde etmek için pnömatiğin gücünü kapalı döngü elektronik kontrolün hassasiyeti ile birleştiren gelişmiş bir kontrol teknolojisi olan servo-pnömatiği açıklar. ↩

Merhaba, ben Chuck, pnömatik sektöründe 15 yıllık deneyime sahip kıdemli bir uzmanım. Bepto Pneumatic'te müşterilerimiz için yüksek kaliteli, kişiye özel pnömatik çözümler sunmaya odaklanıyorum. Uzmanlığım endüstriyel otomasyon, pnömatik sistem tasarımı ve entegrasyonunun yanı sıra temel bileşen uygulaması ve optimizasyonunu kapsıyor. Herhangi bir sorunuz varsa veya proje ihtiyaçlarınızı görüşmek isterseniz, lütfen chuck@bepto.com adresinden benimle iletişime geçmekten çekinmeyin.