هل تواجه صعوبة في التنبؤ بالأداء الفعلي للأسطوانة الهوائية؟ يخطئ العديد من المهندسين في حساب مخرجات القوة ومتطلبات الضغط، مما يؤدي إلى تعطل النظام ووقت تعطل مكلف. ولكن هناك طريقة بسيطة لإتقان هذه الحسابات.
تعمل الأسطوانات الهوائية وفقًا للمبادئ الفيزيائية الأساسية، وبشكل أساسي قانون باسكال1والتي تنص على أن الضغط المطبق على مائع محصور ينتقل بالتساوي في جميع الاتجاهات. وهذا يسمح لنا بحساب قوة الأسطوانة بضرب الضغط في مساحة المكبس الفعالة، مع معدلات التدفق ووحدات الضغط التي تتطلب تحويلات دقيقة لتصميم نظام دقيق.
لقد أمضيتُ أكثر من عقد من الزمن في مساعدة العملاء على تحسين أنظمتهم الهوائية، ورأيتُ كيف يمكن لفهم هذه المبادئ الأساسية أن يحول موثوقية النظام. دعني أشاركك المعرفة العملية التي ستساعدك على تجنب الأخطاء الشائعة التي أراها كل يوم.
جدول المحتويات
- كيف يحدد قانون باسكال ناتج قوة الأسطوانة؟
- ما العلاقة بين تدفق الهواء والضغط في الأسطوانات؟
- لماذا يعد فهم تحويل وحدة الضغط أمرًا بالغ الأهمية لتصميم النظام؟
- الخاتمة
- الأسئلة الشائعة حول الفيزياء في الأنظمة الهوائية
كيف يحدد قانون باسكال ناتج قوة الأسطوانة؟
يعد فهم قانون باسكال أمرًا أساسيًا للتنبؤ بأداء الأسطوانة وتحسينه في أي نظام هوائي.
ينص قانون باسكال على أن الضغط المؤثر على مائع في نظام مغلق ينتقل بالتساوي في جميع أنحاء المائع. بالنسبة للأسطوانات التي تعمل بالهواء المضغوط، هذا يعني أن ناتج القوة يساوي الضغط مضروبًا في مساحة المكبس الفعالة (F = P × A). هذه العلاقة البسيطة هي الأساس لجميع حسابات قوة الأسطوانة.
اشتقاق حساب القوة الحسابية
دعونا نحلل الاشتقاق الرياضي لحسابات قوة الأسطوانة:
معادلة القوة الأساسية
المعادلة الأساسية لقوة الأسطوانة هي
و = ص × أ
أين:
- F = ناتج القوة (نيوتن)
- P = الضغط (باسكال)
- A = مساحة المكبس الفعالة (م²)
اعتبارات المنطقة الفعالة
تختلف المساحة الفعالة باختلاف نوع الأسطوانة واتجاهها:
| نوع الاسطوانة | قوة التمديد | قوة السحب |
|---|---|---|
| أحادية المفعول | ف × أ | قوة الزنبرك فقط |
| مزدوج المفعول (قياسي) | ف × أ | ف × (أ - أ) |
| مزدوج المفعول (بدون قضيب) | ف × أ | ف × أ |
أين:
- أ = كامل مساحة المكبس
- أ = مساحة المقطع العرضي للقضيب
قمت ذات مرة بالتشاور مع مصنع في أوهايو كان يعاني من عدم كفاية القوة في تطبيق الكبس الخاص بهم. كانت حساباتهم تبدو صحيحة على الورق، لكن الأداء الفعلي كان ناقصًا. وعند التحقيق، اكتشفت أنهم كانوا يستخدمون مقياس الضغط2 في حساباتهم بدلاً من الضغط المطلق، ولم يأخذوا في الحسبان مساحة القضيب أثناء السحب. بعد إعادة الحساب باستخدام المعادلة الصحيحة وقيم الضغط الصحيحة، تمكنا من تحديد حجم نظامهم بشكل صحيح، مما أدى إلى زيادة الإنتاجية بمقدار 23%.
أمثلة عملية لحساب القوة العملية
دعونا نتناول بعض الحسابات الواقعية:
مثال 1: قوة التمديد في أسطوانة قياسية
بالنسبة للأسطوانة التي تحتوي على:
- قطر التجويف = 50 مم (نصف القطر = 25 مم = 0.025 م)
- ضغط التشغيل = 6 بار (600,000 باسكال)
منطقة المكبس هي:
أ = π = π × r² = π × (0.025)² = 0.001963 م²
قوة التمديد هي:
F = P × A = 600,000 باسكال × 0.001963 م² = 1,178 نيوتن ≈ 118 كجم قوة
مثال 2: قوة التراجع في نفس الأسطوانة
إذا كان قطر القضيب 20 مم (نصف القطر = 10 مم = 0.01 م):
منطقة القضيب هي:
أ = π × r² = π × (0.01)² = 0.000314 م²
منطقة التراجع الفعال هي:
أ - أ = 0.001963 - 0.000314 = 0.001649 م²
قوة التراجع هي:
F = P × (A - a) = 600,000 باسكال × 0.001649 م² = 989 نيوتن ≈ 99 كجم قوة
عوامل الكفاءة في تطبيقات العالم الحقيقي
في التطبيقات العملية، تؤثر عدة عوامل على حساب القوة النظرية:
خسائر الاحتكاك
يقلل الاحتكاك بين مانع تسرب المكبس وجدار الأسطوانة من القوة الفعالة:
| نوع الختم | عامل الكفاءة النموذجي |
|---|---|
| معيار NBR | 0.85-0.90 |
| مادة PTFE منخفضة الاحتكاك | 0.90-0.95 |
| الأختام القديمة/البالية | 0.70-0.85 |
معادلة القوة العملية
معادلة القوة الواقعية الأكثر دقة هي
F_فعلي = η × P × A
أين:
- η (eta) = عامل الكفاءة (عادةً 0.85-0.95)
ما العلاقة بين تدفق الهواء والضغط في الأسطوانات؟
إن فهم العلاقة بين معدل التدفق والضغط أمر بالغ الأهمية لتحديد حجم أنظمة إمداد الهواء والتنبؤ بسرعة الأسطوانة.
يرتبط تدفق الهواء والضغط في الأنظمة الهوائية ارتباطًا عكسيًا - فكلما زاد الضغط، يقل التدفق عادةً. وتتبع هذه العلاقة قوانين الغاز وتتأثر بالقيود ودرجة الحرارة وحجم النظام. يتطلب التشغيل السليم للأسطوانة موازنة هذه العوامل لتحقيق السرعة والقوة المطلوبة.
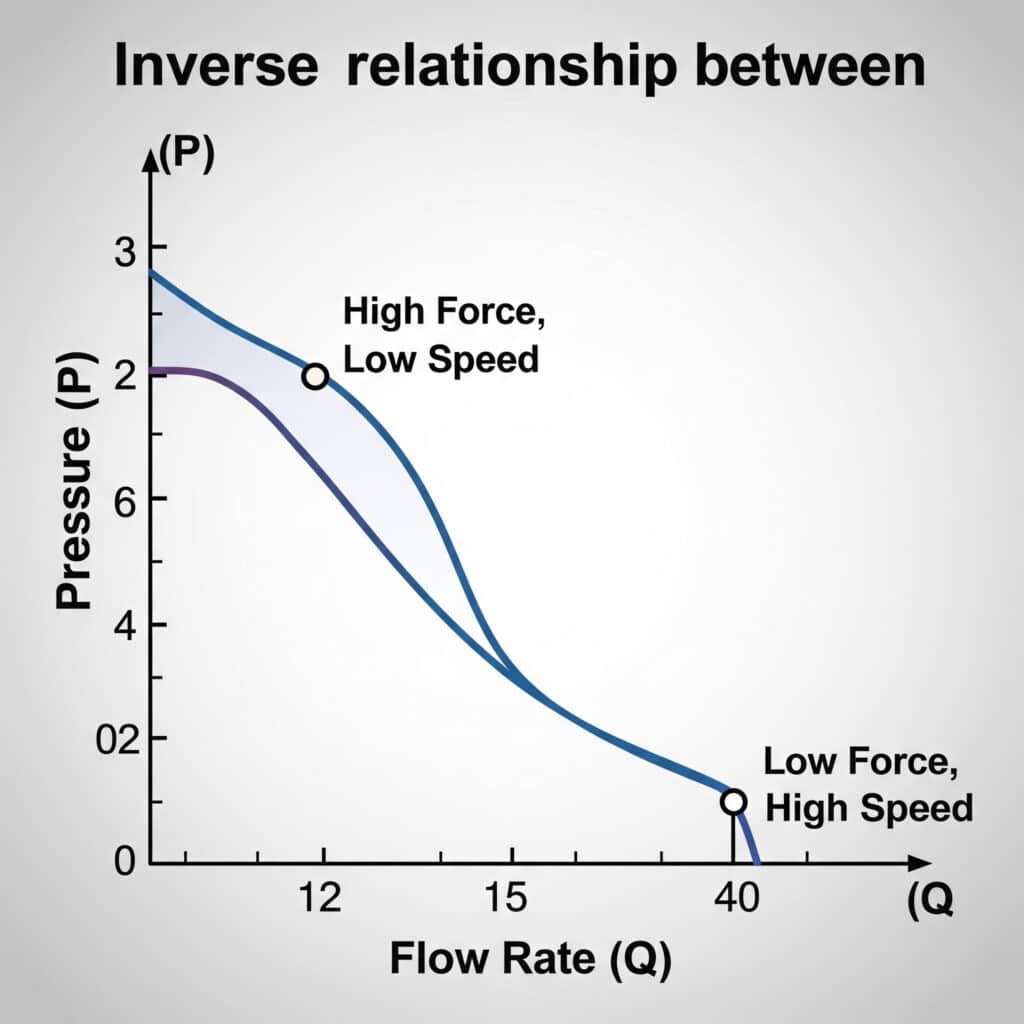
جدول التحويل بين التدفق والضغط
يوضح هذا الجدول المرجعي العملي العلاقة بين معدل التدفق وانخفاض الضغط عبر مكونات النظام المختلفة:
| حجم الأنبوب (مم) | معدل التدفق (لتر/دقيقة) | انخفاض الضغط (بار/متر) عند إمداد 6 بار |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
رياضيات التدفق والضغط
تتبع العلاقة بين السريان والضغط العديد من قوانين الغازات:
معادلة بويزويل3 للتدفق الصفحي
للتدفق الصفحي عبر الأنابيب:
س = (π × r⁴ × ΔP) / (8 × η × L)
أين:
- Q = معدل التدفق الحجمي
- r = نصف قطر الأنبوب
- ΔP = فرق الضغط
- η = اللزوجة الديناميكية
- L = طول الأنبوب
معامل التدفق (Cv)4 الطريقة
بالنسبة للمكونات مثل الصمامات:
س = Cv × ΔP
أين:
- س = معدل التدفق
- Cv = معامل التدفق
- ΔP = انخفاض الضغط عبر المكوِّن
حساب سرعة الأسطوانة
تعتمد سرعة الأسطوانة الهوائية على معدل التدفق ومساحة الأسطوانة:
v = Q / A
أين:
- v = سرعة الأسطوانة (م/ث)
- س = معدل التدفق (م³/ث)
- أ = مساحة المكبس (م²)
خلال مشروع حديث في منشأة تعبئة وتغليف في فرنسا، واجهت حالة كانت فيها أسطوانات العميل التي لا تحتوي على قضبان تتحرك ببطء شديد على الرغم من الضغط الكافي. ومن خلال تحليل نظامهم باستخدام حسابات التدفق والضغط الخاصة بنا، حددنا خطوط الإمداد صغيرة الحجم مما تسبب في انخفاض كبير في الضغط. وبعد الترقية من أنابيب 6 مم إلى أنابيب 10 مم، تحسّن زمن الدورة لديهم بمقدار 40%، مما أدى إلى زيادة الطاقة الإنتاجية بشكل كبير.
اعتبارات التدفق الحرجة
تؤثر عدة عوامل على العلاقة بين التدفق والضغط في الأنظمة الهوائية:
ظاهرة التدفق المختنق5
عندما تتجاوز نسبة الضغط قيمة حرجة (0.53 تقريبًا للهواء)، يصبح التدفق "مختنقًا" ولا يمكن أن يزيد بغض النظر عن تخفيض الضغط في المصب.
تأثيرات درجة الحرارة
يتأثر معدل التدفق بدرجة الحرارة وفقًا للعلاقة:
q₂ = q₁ × √ (t₂/t₁)
أين:
- Q₁، Q₂ = معدلات التدفق عند درجات حرارة مختلفة
- T₁، T₂ = درجات الحرارة المطلقة
لماذا يعد فهم تحويل وحدة الضغط أمرًا بالغ الأهمية لتصميم النظام؟
يعد التنقل بين وحدات الضغط المختلفة المستخدمة في جميع أنحاء العالم أمرًا ضروريًا لتصميم النظام المناسب والتوافق الدولي.
يعد تحويل وحدة الضغط أمرًا بالغ الأهمية لأن المكونات والمواصفات الهوائية تستخدم وحدات مختلفة حسب المنطقة والصناعة. يمكن أن يؤدي سوء تفسير الوحدات إلى أخطاء حسابية كبيرة، مع عواقب خطيرة محتملة. يضيف التحويل بين الضغط المطلق والمقياس والضغط التفاضلي طبقة أخرى من التعقيد.
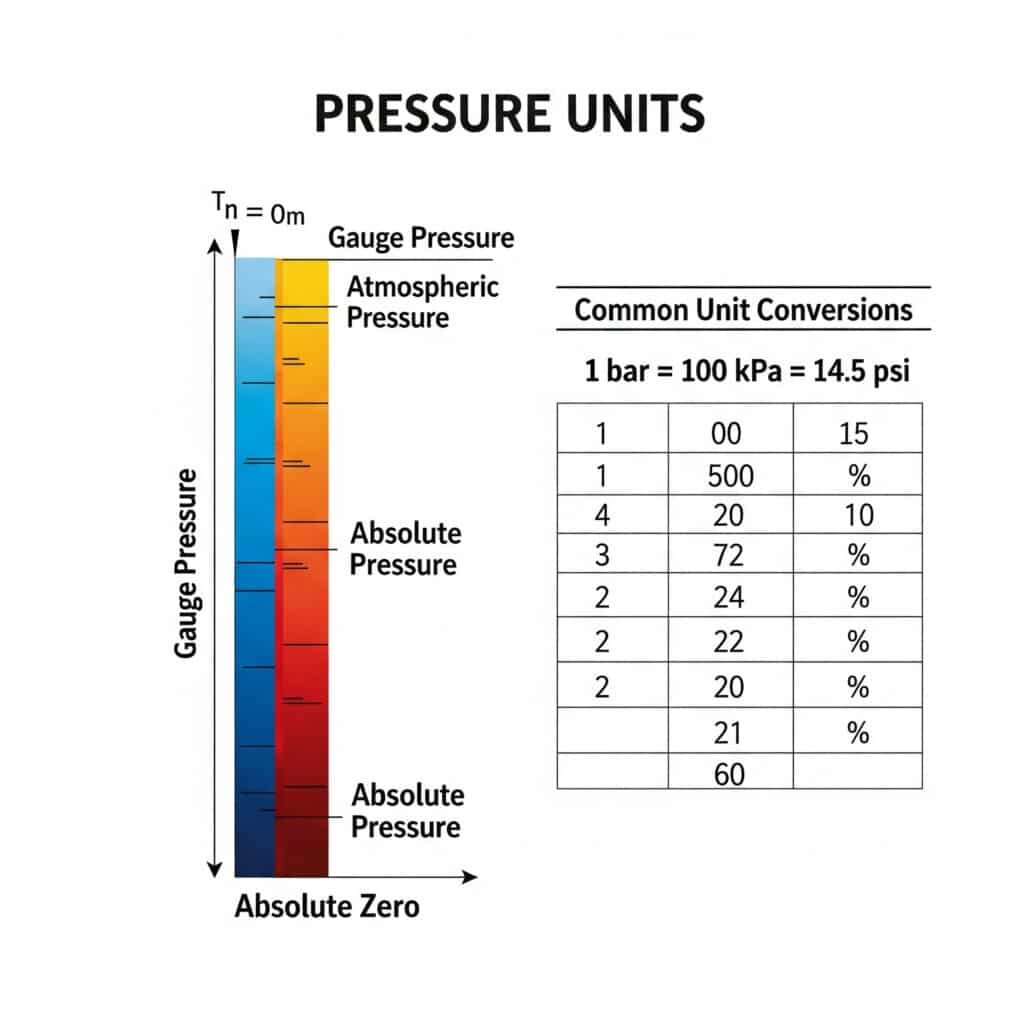
دليل تحويل وحدة الضغط المطلق
يساعد جدول التحويل الشامل هذا في التنقل بين وحدات الضغط المختلفة المستخدمة عالميًا:
| الوحدة | الرمز | ما يعادلها في Pa | ما يعادلها في البار | المعادل بوحدة رطل لكل بوصة مربعة |
|---|---|---|---|---|
| باسكال | با | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| البار | شريط | 1 × 10⁵ | 1 | 14.5038 |
| رطل لكل بوصة مربعة | رطل | 6,894.76 | 0.0689476 | 1 |
| قوة الكيلوغرام لكل سم مربع | كجم/سم² | 98,066.5 | 0.980665 | 14.2233 |
| ميغاباسكال | ميجا باسكال | 1 × 10⁶ | 10 | 145.038 |
| الغلاف الجوي | جهاز الصراف الآلي | 101,325 | 1.01325 | 14.6959 |
| تور | تور | 133.322 | 0.00133322 | 0.0193368 |
| مليمتر من الزئبق | مم زئبق | 133.322 | 0.00133322 | 0.0193368 |
| بوصة من الماء | فيH₂O | 249.089 | 0.00249089 | 0.0361274 |
الضغط المطلق مقابل الضغط المقياسي
يعد فهم الفرق بين الضغط المطلق والضغط المقياسي أمرًا أساسيًا:
حاسبة تحويل الضغط
محول وحدة الضغط
محول معدل تدفق الأسطوانة
صيغ التحويل
- P_المطلق = P_gauge + P_atmospheric
- P_gauge = P_المطلق - P_atmospheric
حيث يكون الضغط الجوي القياسي تقريباً:
- 1.01325 بار
- 14.7 رطل لكل بوصة مربعة
- 101,325 101,325 باسكال
لقد عملت ذات مرة مع فريق هندسي في ألمانيا كان قد اشترى أسطواناتنا بدون قضيب ولكنه أبلغ عن عدم تحقيق القوة المتوقعة. بعد إجراء بعض استكشاف الأخطاء وإصلاحها، اكتشفنا أنهم كانوا يستخدمون مخططات القوة الخاصة بنا (التي كانت تعتمد على ضغط المقياس) ولكنهم كانوا يدخلون قيم الضغط المطلق. تسبب سوء الفهم البسيط هذا في سوء تقدير 1 بار في توقعات القوة لديهم. بعد توضيح مرجع الضغط، كان أداء نظامهم كما هو محدد تمامًا.
أمثلة على التحويل العملي
دعنا نستعرض بعض سيناريوهات التحويل الشائعة:
مثال 1: تحويل ضغط العمل عبر الوحدات
أسطوانة مصنفة لضغط تشغيل أقصى 0.7 ميجا باسكال:
في البار:
0.7 ميجا باسكال × 10 بار/ميجا باسكال = 7 بار
في psi:
0.7 ميجا باسكال × 145.038 رطل/ميجاباسكال = 101.5 رطل لكل بوصة مربعة
مثال 2: التحويل من الضغط المقياسي إلى الضغط المطلق
نظام يعمل بضغط قياس 6 بار:
في الضغط المطلق (بار):
6 بار_مقياس + 1.01325 بار_غلاف جوي = 7.01325 بار_مطلق
مثال 3: التحويل من kgf/cm² إلى MPa
أسطوانة يابانية محددة بـ 7 كجم/سم²:
في ميجا باسكال:
7 كجم قدم/سم² × 0.0980665 ميجا باسكال/(كجم قدم/سم²) = 0.686 ميجا باسكال
تفضيلات وحدة الضغط الإقليمية
تستخدم المناطق المختلفة عادةً وحدات ضغط مختلفة:
| المنطقة | وحدات الضغط المشتركة |
|---|---|
| أمريكا الشمالية | رطل لكل بوصة مربعة (psi)، بوصة زئبقية، بوصة زئبقية، بوصة هيدروجينية |
| أوروبا | بار، باسكال، ملي بار |
| اليابان | كجم/سم²، ميجا باسكال |
| الصين | ميجا باسكال، بار |
| المملكة المتحدة | بار، رطل لكل بوصة مربع، باسكال |
قياس الضغط في التوثيق
عند توثيق مواصفات الضغط، من الضروري الإشارة بوضوح إلى:
- القيمة العددية
- وحدة القياس
- سواء كان ضغطًا مقياسيًا (g) أو ضغطًا مطلقًا (a)
على سبيل المثال:
- 6 بار_ج (الضغط المقياسي، 6 بار فوق الضغط الجوي)
- 7.01 بار_أ (الضغط المطلق، الضغط الكلي بما في ذلك الضغط الجوي)
الخاتمة
يعد فهم الفيزياء الكامنة وراء الأسطوانات الهوائية - بدءًا من حسابات قوة قانون باسكال إلى علاقات التدفق والضغط وتحويلات وحدة الضغط - أمرًا ضروريًا لتصميم النظام المناسب واستكشاف الأخطاء وإصلاحها. تساعد هذه المبادئ الأساسية في ضمان تقديم الأنظمة الهوائية للأداء المتوقع بشكل موثوق وفعال.
الأسئلة الشائعة حول الفيزياء في الأنظمة الهوائية
كيف يمكنني حساب قوة الخرج لأسطوانة هوائية بدون قضيب؟
لحساب قوة الخرج لأسطوانة هوائية بدون قضيب، اضرب ضغط التشغيل في مساحة المكبس الفعالة (F = P × A). على سبيل المثال، أسطوانة بدون قضيب ذات تجويف 50 مم (0.001963 م²) تعمل عند 6 بار (600000 باسكال) ستنتج قوة تبلغ 1178 نيوتن تقريبًا. على عكس الأسطوانات التقليدية، عادةً ما يكون للأسطوانات بدون قضيب نفس المساحة الفعالة في كلا الاتجاهين.
كيف يمكنني حساب قوة الخرج لأسطوانة هوائية بدون قضيب؟
لحساب قوة الخرج لأسطوانة هوائية بدون قضيب، اضرب ضغط التشغيل في مساحة المكبس الفعالة (F = P × A). على سبيل المثال، أسطوانة بدون قضيب ذات تجويف 50 مم (0.001963 م²) تعمل عند 6 بار (600000 باسكال) ستنتج قوة تبلغ 1178 نيوتن تقريبًا. على عكس الأسطوانات التقليدية، عادةً ما يكون للأسطوانات بدون قضيب نفس المساحة الفعالة في كلا الاتجاهين.
ما الفرق بين الضغط المقياسي والضغط المطلق؟
يقيس الضغط المقياسي (bar_g، psi_g) الضغط بالنسبة إلى الضغط الجوي، حيث يساوي الضغط الجوي صفرًا. يقيس الضغط المطلق (bar_a، psi_a) الضغط بالنسبة إلى فراغ مثالي، وهو ما يساوي صفرًا. للتحويل من الضغط المقياسي إلى الضغط المطلق، أضف الضغط الجوي (حوالي 1.01325 بار أو 14.7 رطل لكل بوصة مربعة) إلى قراءة المقياس.
كيف يؤثر تدفق الهواء على سرعة الأسطوانة؟
تتناسب سرعة الأسطوانة طرديًا مع معدل تدفق الهواء وعكسيًا مع مساحة المكبس (v = Q/A). سيحدّ معدل التدفق غير الكافي بسبب خطوط الإمداد الصغيرة الحجم أو التركيبات المقيدة أو الصمامات غير الملائمة من سرعة الأسطوانة بغض النظر عن الضغط. على سبيل المثال، سينتج معدل تدفق قدره 20 لتر/ثانية من خلال أسطوانة بمساحة مكبس تبلغ 0.002 متر مربع سرعة تبلغ 10 أمتار/ثانية.
لماذا تتحرك الأسطوانات الهوائية أحياناً أبطأ من المحسوبة؟
قد تتحرك الأسطوانات الهوائية أبطأ من المحسوبة بسبب عدة عوامل: قيود إمدادات الهواء التي تسبب انخفاض الضغط، أو الاحتكاك الداخلي من موانع التسرب، أو الأحمال الميكانيكية التي تتجاوز الحسابات، أو التسرب الذي يقلل من الضغط الفعال، أو تأثيرات درجة الحرارة على كثافة الهواء. بالإضافة إلى ذلك، غالبًا ما تحد معاملات تدفق الصمامات من معدل التدفق الفعلي المتاح للأسطوانة.
كيف يمكنني التحويل بين وحدات الضغط المختلفة للمواصفات الدولية؟
للتحويل بين وحدات الضغط، استخدم عوامل الضرب: 1 بار = 100,000 باسكال = 0.1 ميجا باسكال = 14.5038 رطل لكل بوصة مربعة = 1.01972 كجم من البوصة المربعة. تحقق دائمًا مما إذا كان الضغط محددًا بوحدة قياس أو مطلق، حيث يمكن أن يؤثر هذا التمييز بشكل كبير على الحسابات. على سبيل المثال، 6 بار_ج يساوي 7.01325 بار_أ في الظروف الجوية القياسية.
ما العلاقة بين حجم تجويف الأسطوانة وقوة الخرج؟
إن العلاقة بين حجم تجويف الأسطوانة ومخرجات القوة هي علاقة تربيعية - حيث إن مضاعفة قطر التجويف يزيد من مخرجات القوة بمقدار أربعة أضعاف (نظرًا لأن المساحة = π × r²). على سبيل المثال، عند ضغط تشغيل يبلغ 6 بار، تنتج الأسطوانة ذات التجويف 40 مم قوة تبلغ 754 نيوتن تقريبًا، بينما تنتج الأسطوانة ذات التجويف 80 مم حوالي 3016 نيوتن، أي ما يقرب من أربعة أضعاف.
-
يقدم شرحاً تفصيلياً لقانون باسكال، وهو مبدأ أساسي في ميكانيكا الموائع الذي يعد أساس نقل الطاقة الهيدروليكية والهوائية. ↩
-
يقدم تعريفًا واضحًا ومقارنة واضحة بين الضغط المقياسي والضغط المطلق، وهو تمييز حاسم لإجراء حسابات هندسية دقيقة لأن الضغط المقياسي نسبي بالنسبة للضغط الجوي. ↩
-
يشرح اشتقاق وتطبيق قانون بويزويل الذي يصف انخفاض ضغط مائع غير قابل للانضغاط ونيوتوني يسري عبر أنبوب أسطواني طويل في النظام الصفحي. ↩
-
يوفر تعريفًا تقنيًا لمعامل التدفق (Cv)، وهو مقياس إمبراطوري يوفر طريقة موحدة لمقارنة سعات التدفق للصمامات المختلفة. ↩
-
تفاصيل فيزياء السريان المختنق، وهي حالة ديناميكا الموائع التي تحد من معدل السريان الكتلي لمائع قابل للانضغاط عبر قيد عندما تصل السرعة إلى سرعة الصوت. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська 