
Avez-vous déjà remarqué de mystérieuses vibrations dans vos lignes pneumatiques ? Ou des variations de force inexpliquées dans vos cylindres malgré une pression d'alimentation stable ? Ces phénomènes ne sont pas le fruit du hasard : ils sont le résultat d'ondes de pression qui se propagent dans votre système, créant des effets qui peuvent aller d'inefficacités mineures à des défaillances catastrophiques.
Les fluctuations de pression dans les systèmes pneumatiques sont des phénomènes ondulatoires qui se propagent à des vitesses proches de la vitesse de la lumière. vitesse du son1Les effets dynamiques, y compris la résonance, sont ainsi créés, ondes stationnaires2et l'amplification de la pression. Il est essentiel de comprendre ces fluctuations, car elles peuvent entraîner la fatigue des composants, l'instabilité des commandes et l'augmentation de la pression. pertes d'énergie de 10-25% dans des systèmes industriels typiques3.
Le mois dernier, j'ai conseillé une usine d'assemblage automobile du Tennessee dont le système de serrage pneumatique critique connaissait des variations de force intermittentes malgré une pression d'alimentation stable. L'équipe de maintenance avait remplacé les vannes, les régulateurs et même l'ensemble du système. unité de préparation de l'air4 sans succès. En analysant la dynamique des ondes de pression - en particulier les modèles d'ondes stationnaires dans leurs lignes d'approvisionnement - nous avons identifié qu'ils fonctionnaient à une fréquence qui créait des interférences destructrices au niveau du cylindre. Un simple ajustement de la longueur de la ligne a permis d'éliminer le problème et d'éviter des semaines de retard dans la production. Laissez-moi vous montrer comment la compréhension de la théorie des fluctuations de pression peut transformer la fiabilité de votre système pneumatique.
Table des matières
- Vitesse de propagation des ondes : À quelle vitesse les perturbations de la pression se déplacent-elles dans votre système ?
- Vérification des ondes stationnaires : Comment les fréquences résonnantes créent-elles des problèmes de performance ?
- Méthodes d'atténuation des impulsions : Quelles techniques permettent d'atténuer efficacement les oscillations de pression destructrices ?
- Conclusion
- FAQ sur les variations de pression dans les systèmes pneumatiques
Vitesse de propagation des ondes : À quelle vitesse les perturbations de la pression se déplacent-elles dans votre système ?
Il est fondamental de comprendre la vitesse de propagation des perturbations de pression dans les systèmes pneumatiques pour prévoir et contrôler leurs effets. La vitesse de propagation détermine le temps de réponse du système, les fréquences de résonance et le potentiel d'interférence destructive.
Dans les systèmes pneumatiques, les ondes de pression se déplacent à la vitesse du son dans le milieu gazeux, qui peut être calculée à l'aide de la formule c = √(γRT), où γ est le rapport de chaleur spécifique, R est la constante de gaz spécifique et T est la température absolue. Pour l'air à 20°C, cela équivaut à environ 343 m/s, bien que cette vitesse soit modifiée par des facteurs tels que l'élasticité du tuyau, la compressibilité du gaz et les conditions d'écoulement.
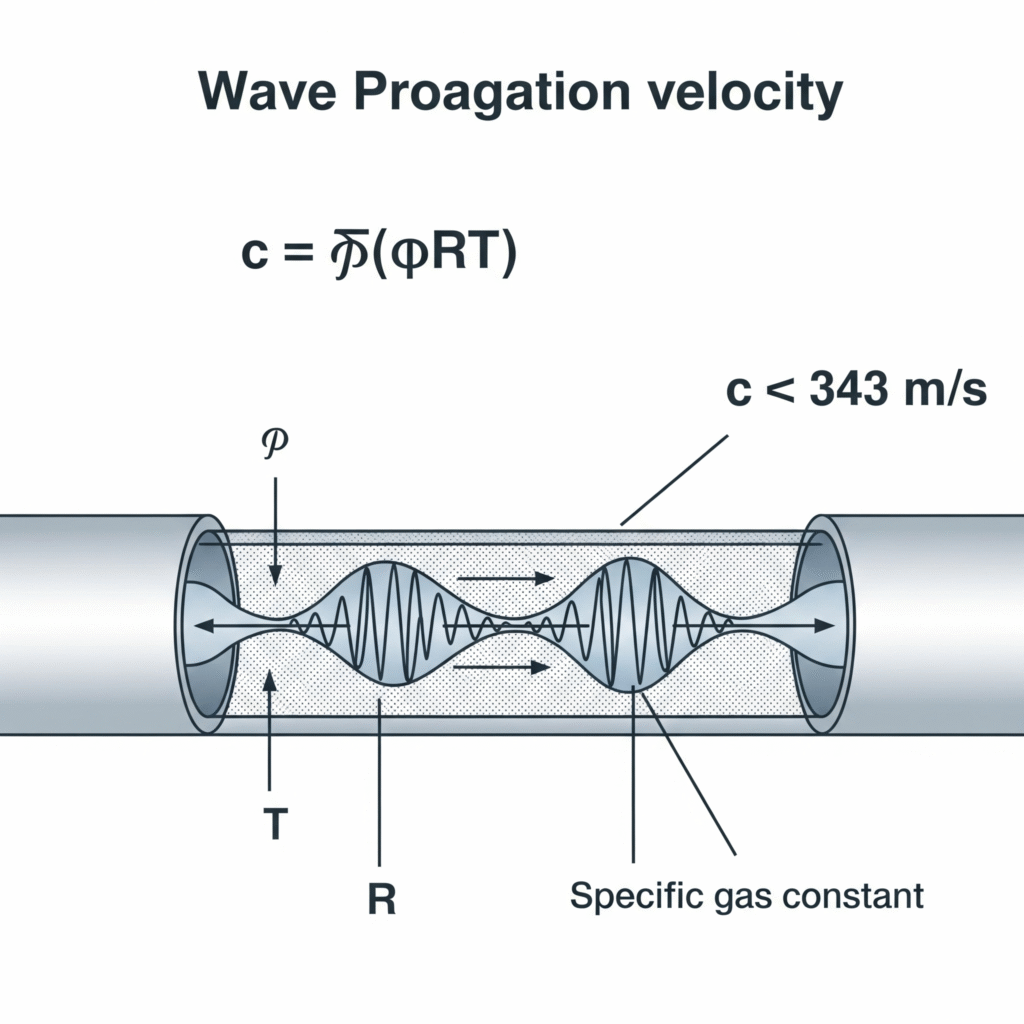
J'ai récemment participé au dépannage d'une machine d'assemblage de précision en Suisse où les pinces pneumatiques présentaient un délai de 12 ms entre l'activation et l'application de la force - une éternité dans un environnement de production à grande vitesse. Les ingénieurs avaient supposé que la transmission de la pression était instantanée. En mesurant la vitesse réelle de propagation de l'onde dans leur système (328 m/s) et en tenant compte de la longueur de ligne de 4 mètres, nous avons calculé un temps de transmission théorique de 12,2 ms, ce qui correspond presque exactement au délai observé. Le fait de rapprocher les vannes des actionneurs a permis de réduire ce délai à 3 ms et d'augmenter le taux de production de 14%.
Equations fondamentales de la vitesse des ondes
L'équation de base de la vitesse de propagation des ondes de pression dans un gaz est la suivante :
c = √(γRT)
Où ?
- c = Vitesse de propagation des ondes (m/s)
- γ = Rapport de chaleur spécifique (1,4 pour l'air)
- R = Constante spécifique des gaz (287 J/kg-K pour l'air)
- T = Température absolue (K)
Pour l'air à 20°C (293K), cela donne :
c = √(1,4 × 287 × 293) = 343 m/s
Vitesse d'onde modifiée dans les lignes pneumatiques
Dans les systèmes pneumatiques réels, la vitesse d'onde effective est modifiée par l'élasticité du tuyau et d'autres facteurs selon la formule :
c_eff = c / √ (1 + (Dψ/Eh))
Où ?
- c_eff = Vitesse effective de l'onde (m/s)
- D = Diamètre du tube (m)
- ψ = Facteur de compressibilité du gaz
- E = Module d'élasticité du matériau de la conduite (Pa)
- h = Epaisseur de la paroi du tube (m)
Effets de la température et de la pression sur la vitesse des ondes
La vitesse de l'onde varie en fonction des conditions de fonctionnement :
| Température | Pression | Vitesse d'onde dans l'air | Implication pratique |
|---|---|---|---|
| 0°C (273K) | 1 bar | 331 m/s | Réponse plus lente dans les environnements froids |
| 20°C (293K) | 1 bar | 343 m/s | Condition de référence standard |
| 40°C (313K) | 1 bar | 355 m/s | Réponse plus rapide dans les environnements chauds |
| 20°C (293K) | 6 bars | 343 m/s* | La pression n'a qu'un effet direct minime sur la vitesse. |
*Note : Alors que la vitesse de base de l'onde est indépendante de la pression, la vitesse effective dans les systèmes réels peut être affectée par des changements induits par la pression dans l'élasticité de la conduite et le comportement du gaz.
Calcul pratique du temps de propagation des ondes
Pour un système pneumatique avec :
- Longueur de la ligne (L) : 5 mètres
- Température de fonctionnement : 20°C (c = 343 m/s)
- Matériau du tuyau : Tube en polyuréthane (modifie la vitesse d'environ 5%)
La vitesse effective de l'onde serait :
c_eff = 343 × 0,95 = 326 m/s
Et le temps de propagation de l'onde serait :
t = L/c_eff = 5/326 = 0,0153 seconde (15,3 millisecondes)
Cela représente le temps minimum nécessaire pour qu'un changement de pression se produise d'un bout à l'autre de la ligne, un facteur critique dans les applications à grande vitesse.
Techniques de mesure de la vitesse des ondes
Plusieurs méthodes peuvent être utilisées pour mesurer la vitesse réelle de l'onde dans les systèmes pneumatiques :
Méthode du double capteur de pression
- Installer des capteurs de pression à des distances connues
- Créer une impulsion de pression (ouverture rapide de la vanne)
- Mesurer le délai entre l'augmentation de la pression à chaque capteur
- Calculer la vitesse en divisant la distance par le délai.
Méthode de la fréquence résonnante
- Créer des oscillations de pression dans un tube fermé
- Mesurer la fréquence fondamentale de résonance (f)
- Calculer la vitesse en utilisant c = 2Lf pour un tube fermé.
- Vérifier avec les harmoniques (multiples impairs de la fondamentale)
Méthode de temporisation de la réflexion
- Installer un capteur de pression près d'une vanne
- Créer une impulsion de pression en ouvrant rapidement le robinet
- Mesure du temps entre l'impulsion initiale et l'impulsion réfléchie
- Calculer la vitesse en divisant 2L par le temps de réflexion.
Étude de cas : Impact de la vitesse des vagues sur la réponse du système
Pour un effecteur robotique avec des pinces pneumatiques :
| Paramètres | Modèle original (5m lignes) | Conception optimisée (1m lignes) | Amélioration |
|---|---|---|---|
| Longueur de la ligne | 5 mètres | 1 mètre | Réduction 80% |
| Temps de propagation de l'onde | 15,3 ms | 3,1 ms | 12,2 ms plus rapide |
| Temps de montée en pression | 28 ms | 9 ms | 19 ms plus rapide |
| Stabilité de la force de préhension | ±12% variation | ±3% variation | Amélioration 75% |
| Durée du cycle | 1,2 seconde | 0,95 secondes | 21% plus rapide |
| Taux de production | 3000 pièces/heure | 3780 pièces/heure | 26% augmentation |
Cette étude de cas montre comment la compréhension et l'optimisation de la propagation des ondes peuvent avoir un impact significatif sur les performances du système.
Vérification des ondes stationnaires : Comment les fréquences résonnantes créent-elles des problèmes de performance ?
Les ondes stationnaires se produisent lorsque les ondes de pression se réfléchissent et interfèrent entre elles, créant des modèles fixes de nœuds et d'antinœuds de pression. Ces phénomènes de résonance peuvent entraîner de graves problèmes de performance dans les systèmes pneumatiques s'ils ne sont pas correctement compris et gérés.
Les ondes stationnaires dans les systèmes pneumatiques se produisent lorsque les ondes de pression se réfléchissent aux limites et interfèrent de manière constructive, créant des fréquences de résonance où les fluctuations de pression sont amplifiées. Ces résonances suivent la formule f = nc/2L pour les tubes fermés, où n est le nombre d'harmoniques, c la vitesse de l'onde et L la longueur du tube. La vérification expérimentale au moyen de capteurs de pression, d'accéléromètres et de mesures acoustiques confirme ces prédictions théoriques et oriente les stratégies d'atténuation efficaces.
Lors d'un récent projet avec un fabricant d'appareils médicaux du Massachusetts, son système de positionnement pneumatique de précision présentait de mystérieuses fluctuations de force à des fréquences de fonctionnement spécifiques. En effectuant des tests de vérification des ondes stationnaires, nous avons identifié que leur ligne d'alimentation de 2,1 mètres avait une résonance fondamentale à 81 Hz - correspondant précisément à la fréquence de cycle de leur actionneur. Cette résonance amplifiait les fluctuations de pression de 320%. En ajustant la longueur de la ligne à 1,8 mètre, nous avons éloigné la fréquence de résonance de leur plage de fonctionnement et avons complètement éliminé le problème, améliorant la précision du positionnement de ±0,8 mm à ±0,15 mm.
Principes de base des ondes stationnaires
Les ondes stationnaires se forment lorsque les ondes incidentes et réfléchies interfèrent, créant des configurations fixes de nœuds de pression (fluctuation minimale) et d'antinœuds (fluctuation maximale).
Les fréquences de résonance d'une ligne pneumatique dépendent des conditions aux limites :
Pour une ligne avec des extrémités fermées (le plus souvent dans les systèmes pneumatiques) :
f = nc/2L
Où ?
- f = Fréquence de résonance (Hz)
- n = Nombre harmonique (1, 2, 3, etc.)
- c = Vitesse des vagues (m/s)
- L = Longueur de la ligne (m)
Pour une ligne avec une extrémité ouverte :
f = (2n-1)c/4L
Pour une ligne dont les deux extrémités sont ouvertes (rare en pneumatique) :
f = nc/2L
Méthodes de vérification expérimentale
Plusieurs techniques permettent de vérifier les ondes stationnaires dans les systèmes pneumatiques :
Réseau de capteurs de pression multiples
- Installer des transducteurs de pression à intervalles réguliers le long de la ligne pneumatique
- Exciter le système à l'aide d'un balayage de fréquence ou d'une impulsion
- Enregistrer les fluctuations de pression à chaque endroit
- Cartographier l'amplitude de la pression en fonction de la position pour identifier les nœuds et les antinœuds
- Comparer les fréquences mesurées avec les prévisions théoriques
Corrélation acoustique
- Utiliser des capteurs acoustiques (microphones) pour détecter le son à partir des fluctuations de pression.
- Corrélation entre l'intensité sonore et la fréquence de fonctionnement
- Identifier les pics d'intensité sonore correspondant aux fréquences de résonance
- Vérifier que les pics se produisent aux fréquences prévues
Mesures de l'accéléromètre
- Montage d'accéléromètres sur des lignes et des composants pneumatiques
- Mesure de l'amplitude des vibrations sur toute la gamme de fréquences
- Identifier les pics de résonance dans le spectre vibratoire
- Corrélation avec les fréquences prédites des ondes stationnaires
Calcul pratique de la fréquence des ondes stationnaires
Pour un système pneumatique typique avec :
- Longueur de la ligne (L) : 3 mètres
- Vitesse de l'onde (c) : 343 m/s
- Configuration des extrémités fermées
La fréquence fondamentale de résonance serait :
f₁ = c/2L = 343/(2×3) = 57,2 Hz
Et les harmoniques seraient :
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Ces fréquences représentent des points problématiques potentiels où les fluctuations de pression peuvent être amplifiées.
Les ondes stationnaires et leurs effets
| Harmonique | Modèle de nœud/antinoïde | Effets du système | Composants critiques concernés |
|---|---|---|---|
| Fondamental (n=1) | Un antinode de pression au centre | Variations importantes de la pression au milieu de la ligne | Composants en ligne, raccords |
| Deuxième (n=2) | Deux antinodes, nœud au centre | Variations de pression près des extrémités | Vannes, actionneurs, régulateurs |
| Troisième (n=3) | Trois antinodes, deux nœuds | Modèle de pression complexe | Composants multiples du système |
| Quatrième (n=4) | Quatre antinodes, trois nœuds | Oscillations à haute fréquence | Joints, petits composants |
Étude de cas de vérification expérimentale
Pour un système de positionnement pneumatique de précision dont les performances sont irrégulières :
| Paramètres | Prédiction théorique | Mesures expérimentales | Corrélation |
|---|---|---|---|
| Fréquence fondamentale | 81,2 Hz | 79,8 Hz | 98.3% |
| Deuxième harmonique | 162,4 Hz | 160,5 Hz | 98.8% |
| Troisième harmonique | 243,6 Hz | 240,1 Hz | 98.6% |
| Amplification de la pression | 3:1 à la résonance (estimation) | 3,2:1 à la résonance (mesuré) | 93.8% |
| Emplacement des nœuds | 0, 1,05, 2,1 mètres | 0, 1,08, 2,1 mètres | 97.2% |
Cette étude de cas démontre l'excellente concordance entre les prédictions théoriques et les mesures expérimentales des phénomènes d'ondes stationnaires.
Implications pratiques des ondes stationnaires
Les ondes stationnaires posent plusieurs problèmes importants dans les systèmes pneumatiques :
Amplification de la pression
- Les fluctuations peuvent être amplifiées de 3 à 5 fois à la résonance.
- Peut dépasser les pressions nominales des composants
- Crée des variations de force dans les actionneursFatigue des composants
- Les cycles de pression à haute fréquence accélèrent l'usure des joints
- Les vibrations provoquent le desserrage des raccords et des fuites.
- Réduit la durée de vie du système de 30-70% dans les cas gravesInstabilité du contrôle
- Les systèmes de rétroaction peuvent osciller à des fréquences de résonance
- Le contrôle de la position et de la force devient imprévisible
- Peut créer des oscillations qui se renforcent d'elles-mêmesPertes d'énergie
- Les ondes stationnaires représentent de l'énergie piégée
- Peut augmenter la consommation d'énergie de 10-30%
- Réduit l'efficacité globale du système
Méthodes d'atténuation des impulsions : Quelles techniques permettent d'atténuer efficacement les oscillations de pression destructrices ?
Le contrôle des fluctuations de pression est essentiel pour un fonctionnement fiable des systèmes pneumatiques. Diverses méthodes d'atténuation peuvent être employées pour réduire ou éliminer les oscillations de pression problématiques.
L'atténuation des impulsions de pression dans les systèmes pneumatiques peut être obtenue par plusieurs méthodes : des chambres de volume qui absorbent l'énergie par la compression des gaz, des éléments restrictifs qui créent un amortissement par des effets visqueux, des résonateurs accordés qui annulent des fréquences spécifiques et des systèmes d'annulation actifs qui génèrent des contre-impulsions. Pour que l'atténuation soit efficace, il faut que la méthode soit adaptée à la fréquence spécifique et à l'amplitude des fluctuations de pression.
J'ai récemment travaillé avec un fabricant d'équipements d'emballage de l'Illinois dont le système pneumatique à grande vitesse connaissait d'importantes fluctuations de pression qui entraînaient des forces d'étanchéité incohérentes. Ses ingénieurs avaient essayé sans succès des réservoirs de réception de base. Grâce à une analyse détaillée des impulsions de pression, nous avons identifié que leur système comportait plusieurs composantes de fréquence nécessitant différentes approches d'atténuation. En mettant en œuvre une solution hybride combinant un Résonateur de Helmholtz5 accordés à leur oscillation dominante de 112 Hz et à une série d'orifices de restriction, nous avons réduit les fluctuations de pression de 94% et éliminé complètement les incohérences d'étanchéité.
Mécanismes fondamentaux d'atténuation
Plusieurs mécanismes physiques peuvent être utilisés pour atténuer les impulsions de pression :
Atténuation basée sur le volume
Fonctionne grâce à la compressibilité des gaz :
- Fournit un élément de conformité qui absorbe l'énergie de la pression
- Plus efficace pour les fluctuations à faible fréquence
- Mise en œuvre simple avec une perte de charge minimale
Atténuation basée sur la restriction
Fonctionne par dissipation visqueuse :
- Convertit l'énergie de la pression en chaleur par frottement
- Efficace sur une large gamme de fréquences
- Création d'une perte de charge permanente
Atténuation par résonateur
Fonctionne par interférence destructive accordée :
- Annule des composantes de fréquence spécifiques
- Très efficace pour les fréquences ciblées
- Impact minimal sur le débit en régime permanent
Atténuation basée sur les matériaux
Fonctionne grâce à la flexibilité et à l'amortissement des murs :
- Absorbe l'énergie par la déformation des parois
- Atténuation à large bande
- Peut être intégré dans des composants existants
Principes de conception de la chambre de volume
Les chambres de volume (réservoirs de réception) sont les dispositifs d'atténuation les plus courants :
L'efficacité d'une chambre de volume dépend du rapport entre le volume de la chambre et le volume de la ligne :
Rapport d'atténuation = 1 + (Vc/Vl)
Où ?
- Vc = Volume de la chambre
- Vl = Volume de la ligne
Pour l'analyse en fonction de la fréquence, le rapport de transmission est :
TR = 1/√(1 + (ωVc/Zc)²)
Où ?
- ω = Fréquence angulaire (2πf)
- Zc = Impédance caractéristique de la ligne
Élément restrictif Atténuation
Les orifices, les matériaux poreux et les longs passages étroits créent une atténuation par des effets visqueux :
La chute de pression à travers une restriction est la suivante :
ΔP = k(ρv²/2)
Où ?
- k = Coefficient de perte
- ρ = Densité du gaz
- v = Vitesse
L'atténuation fournie augmente avec :
- Vitesse d'écoulement plus élevée
- Plus grande longueur de restriction
- Diamètre de passage plus petit
- Chemin d'écoulement plus tortueux
Systèmes d'atténuation par résonateur
Les résonateurs accordés permettent une atténuation ciblée des fréquences :
Résonateur de Helmholtz
Une chambre de volume avec un col étroit, accordée à une fréquence spécifique :
f = (c/2π)√(A/VL)
Où ?
- f = Fréquence de résonance
- c = Vitesse du son
- A = Surface de la section transversale du cou
- V = Volume de la chambre
- L = Longueur effective du col
Résonateur quart d'onde
Un tube d'une longueur spécifique ouvert à une extrémité :
f = c/4L
Où ?
- L = Longueur du tube
Résonateurs à branches latérales
Plusieurs branches accordées pour un contenu de fréquence complexe :
- Chaque branche cible une fréquence spécifique
- Peut traiter plusieurs harmoniques simultanément
- Impact minimal sur la voie d'écoulement principale
Systèmes d'annulation active
Systèmes avancés générant des contre-impulsions :
Phase de détection
- Détecter les ondes de pression entrantes
- Analyse du contenu en fréquence et de l'amplitudeÉtape de transformation
- Calculer le signal d'annulation requis
- Tenir compte de la dynamique du système et des retardsStade d'actionnement
- Générer des ondes de contre-pression
- Temps précis pour l'interférence destructive
Comparaison des performances d'atténuation
| Méthode | Basse fréquence (<50 Hz) | Fréquence moyenne (50-200 Hz) | Haute fréquence (>200 Hz) | Chute de pression | Complexité |
|---|---|---|---|---|---|
| Chambre de volume | Excellent (>90%) | Modéré (40-70%) | Faible (<30%) | Très faible | Faible |
| Orifice restrictif | Faible (<30%) | Bon (60-80%) | Excellent (>80%) | Haut | Faible |
| Résonateur de Helmholtz | Faible résonance extérieure | Excellent à la résonance | Faible résonance extérieure | Faible | Moyen |
| Tube quart d'onde | Faible résonance extérieure | Excellent à la résonance | Faible résonance extérieure | Faible | Moyen |
| Résonateurs multiples | Modéré (40-60%) | Excellent (>80%) | Bon (60-80%) | Faible | Haut |
| Annulation active | Excellent (>90%) | Excellent (>90%) | Bon (70-85%) | Aucun | Très élevé |
| Systèmes hybrides | Excellent (>90%) | Excellent (>90%) | Excellent (>90%) | Modéré | Haut |
Mise en œuvre pratique de l'atténuation
Pour une atténuation efficace des impulsions de pression :
Caractériser les fluctuations
- Mesure de l'amplitude et de la fréquence
- Identifier les fréquences dominantes
- Déterminer si une atténuation est nécessaire pour la large bande ou pour des fréquences spécifiquesChoisir les méthodes appropriées
- Pour les basses fréquences : Chambres de volume
- Pour des fréquences spécifiques : Résonateurs accordés
- Pour l'atténuation à large bande : Restrictions ou approches hybrides
- Pour les applications critiques : Annulation activeOptimiser le placement
- Près des sources pour éviter la propagation
- Approcher les composants sensibles pour les protéger
- Aux endroits stratégiques pour briser les ondes stationnairesVérifier les performances
- Mesure avant/après l'atténuation
- Confirmer les conditions de fonctionnement
- Veiller à ce qu'il n'y ait pas de conséquences imprévues
Étude de cas : Atténuation multi-méthodes dans l'emballage à grande vitesse
Pour un système d'étanchéité pneumatique à grande vitesse soumis à des fluctuations de pression :
| Paramètres | Avant atténuation | Chambre de post-volume | Après la solution hybride | Amélioration |
|---|---|---|---|---|
| Basse fréquence (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | Réduction 94% |
| Fréquence moyenne (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | Réduction 94% |
| Haute fréquence (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | Réduction 90% |
| Variation de la force de scellement | ±28% | ±22% | ±2,5% | 91% amélioration |
| Taux de rejet des produits | 4.2% | 3.1% | 0.3% | Réduction 93% |
| Efficacité du système | Base de référence | +4% | +12% | Amélioration 12% |
Cette étude de cas montre comment une approche ciblée et multi-méthodes de l'atténuation peut améliorer considérablement les performances du système.
Techniques d'atténuation avancées
Pour les applications particulièrement difficiles :
Atténuation répartie
Utiliser plusieurs petits appareils plutôt qu'un seul grand :
- Place l'atténuation plus près des sources et des composants sensibles
- Casse les ondes stationnaires de manière plus efficace
- Assure la redondance et des performances plus régulières
Amortissement sélectif en fréquence
Cibler des fréquences problématiques spécifiques :
- Utilise plusieurs résonateurs accordés sur différentes fréquences
- Préserver la réponse souhaitée du système tout en éliminant les problèmes
- Minimise l'impact sur les performances globales du système
Systèmes adaptatifs
Réglage de l'atténuation en fonction des conditions d'utilisation :
- Utilise des capteurs pour surveiller les fluctuations de pression
- Réglage automatique des paramètres d'atténuation
- Optimise les performances dans des conditions variables
Conclusion
La compréhension de la théorie des fluctuations de pression - vitesse de propagation des ondes, vérification des ondes stationnaires et méthodes d'atténuation des impulsions - constitue la base d'une conception fiable et efficace des systèmes pneumatiques. En appliquant ces principes, vous pouvez éliminer les mystérieux problèmes de performance, prolonger la durée de vie des composants et améliorer l'efficacité du système tout en garantissant un fonctionnement cohérent dans toutes les conditions d'utilisation.
FAQ sur les variations de pression dans les systèmes pneumatiques
Comment les fluctuations de pression affectent-elles la durée de vie des composants pneumatiques ?
Les fluctuations de pression réduisent considérablement la durée de vie des composants par le biais de plusieurs mécanismes : elles provoquent une usure accélérée des joints en créant des micro-mouvements sur les surfaces d'étanchéité ; elles induisent une fatigue des matériaux dans les membranes et les éléments flexibles par le biais de cycles de contrainte répétés ; elles favorisent le desserrage des raccords filetés par le biais de vibrations ; et elles créent des concentrations de contraintes localisées au niveau des transitions géométriques. Les systèmes soumis à de fortes fluctuations de pression incontrôlées ont généralement une durée de vie des composants 40-70% plus courte que les systèmes correctement amortis, les joints et les membranes étant particulièrement vulnérables.
Quelle est la relation entre la longueur de la ligne et le temps de réponse à la pression dans les systèmes pneumatiques ?
La longueur de la ligne affecte directement le temps de réponse à la pression selon une relation simple : le temps de réponse augmente linéairement avec la longueur de la ligne à un taux déterminé par la vitesse de propagation de l'onde. Pour l'air dans des conditions standard (vitesse de l'onde ≈ 343 m/s), chaque mètre de ligne ajoute environ 2,9 millisecondes de délai de transmission. Cependant, le temps réel de montée en pression est généralement 2 à 5 fois plus long que le temps de transmission initial de l'onde, en raison de la nécessité de réflexions multiples pour égaliser la pression. Cela signifie qu'une ligne de 5 mètres peut avoir un temps de transmission de l'onde de 14,5 ms mais un temps de montée en pression de 30 à 70 ms.
Comment puis-je savoir si mon système pneumatique subit des fluctuations de pression par résonance ?
Les fluctuations de pression résonantes se manifestent généralement par plusieurs symptômes observables : les composants vibrent à des fréquences de fonctionnement spécifiques, mais pas à d'autres ; les performances du système varient de manière incohérente avec des changements mineurs des conditions de fonctionnement ; les conduites pneumatiques émettent des "chants" ou des "sifflements" audibles ; les manomètres affichent des relevés oscillants ; et les performances des actionneurs (vitesse, force) varient de manière cyclique. Pour confirmer la résonance, mesurez la pression en différents points du système à l'aide de transducteurs à réponse rapide (temps de réponse <1ms) et recherchez des ondes stationnaires où l'amplitude de la pression varie en fonction de la position le long de la ligne.
Les fluctuations de pression affectent-elles l'efficacité énergétique des systèmes pneumatiques ?
Les fluctuations de pression ont un impact significatif sur l'efficacité énergétique, la réduisant généralement de 10-25% par le biais de plusieurs mécanismes : elles augmentent les taux de fuite en créant des pics de pression plus élevés ; elles gaspillent de l'énergie dans la compression et l'expansion cycliques ; elles provoquent une augmentation de la friction dans les composants en raison des vibrations ; et elles conduisent souvent les opérateurs à augmenter la pression d'alimentation pour compenser les problèmes de performance. En outre, les turbulences et la séparation des flux créées par les fluctuations de pression transforment l'énergie utile de la pression en chaleur perdue. Une atténuation adéquate des fluctuations de pression peut améliorer l'efficacité du système de 5-15% sans autre changement.
Comment les changements de température affectent-ils le comportement des ondes de pression dans les systèmes pneumatiques ?
La température a un impact significatif sur le comportement des ondes de pression par le biais de plusieurs mécanismes : elle affecte directement la vitesse de propagation des ondes (environ +0,6 m/s par °C d'augmentation) ; elle modifie la densité et la viscosité des gaz, ce qui altère les caractéristiques d'amortissement ; elle modifie les propriétés élastiques des conduites pneumatiques, ce qui affecte la réflexion et la transmission des ondes ; et elle déplace les fréquences de résonance (environ +0,17% par °C). Cette sensibilité à la température signifie qu'un système qui fonctionne parfaitement à 20°C peut connaître des résonances problématiques lorsqu'il fonctionne à 40°C, ou que des dispositifs d'atténuation réglés pour des conditions hivernales peuvent s'avérer inefficaces en été.
-
Explique en détail la physique de la vitesse du son, son calcul et les facteurs qui l'influencent. ↩
-
Offre une compréhension fondamentale des phénomènes d'ondes stationnaires, y compris la façon dont elles sont formées à partir d'interférences et leurs caractéristiques clés telles que les nœuds et les antinœuds. ↩
-
Fournit des preuves et des études industrielles qui vérifient la gamme typique des pertes d'énergie causées par des inefficacités telles que les fluctuations de pression dans les systèmes pneumatiques. ↩
-
Explique les composants et la fonction d'une unité de préparation de l'air (FRL), qui est essentielle pour maintenir la qualité de l'air dans les systèmes pneumatiques. ↩
-
Offre une explication approfondie des principes qui sous-tendent le résonateur de Helmholtz, un dispositif essentiel pour l'atténuation ciblée des fréquences dans les systèmes acoustiques et fluides. ↩


