
Avez-vous du mal à prévoir les performances réelles de votre vérin pneumatique ? De nombreux ingénieurs calculent mal les forces de sortie et les pressions requises, ce qui entraîne des défaillances du système et des temps d'arrêt coûteux. Mais il existe un moyen simple de maîtriser ces calculs.
Les vérins pneumatiques fonctionnent selon des principes physiques fondamentaux, principalement Loi de Pascal1La force d'un vérin est égale à celle d'un piston, ce qui signifie que la pression appliquée à un fluide confiné est transmise de manière égale dans toutes les directions. Cela nous permet de calculer la force du vérin en multipliant la pression par la surface effective du piston, les débits et les unités de pression nécessitant des conversions précises pour une conception exacte du système.
J'ai passé plus d'une décennie à aider mes clients à optimiser leurs systèmes pneumatiques et j'ai vu comment la compréhension de ces principes de base peut transformer la fiabilité du système. Laissez-moi partager avec vous les connaissances pratiques qui vous aideront à éviter les erreurs courantes que je vois tous les jours.
Table des matières
- Comment la loi de Pascal détermine-t-elle la puissance du vérin ?
- Quelle est la relation entre le débit d'air et la pression dans les cylindres ?
- Pourquoi la compréhension de la conversion des unités de pression est-elle essentielle pour la conception des systèmes ?
- Conclusion
- FAQ sur la physique des systèmes pneumatiques
Comment la loi de Pascal détermine-t-elle la puissance du vérin ?
La compréhension de la loi de Pascal est fondamentale pour prévoir et optimiser les performances des vérins dans tout système pneumatique.
La loi de Pascal stipule que la pression exercée sur un fluide dans un système fermé est transmise de manière égale dans tout le fluide. Pour les vérins pneumatiques, cela signifie que la force produite est égale à la pression multipliée par la surface effective du piston (F = P × A). Cette relation simple est à la base de tous les calculs de force des vérins.

Calcul de la force Dérivation
Analysons la dérivation mathématique des calculs de la force du cylindre :
Équation de base des forces
L'équation fondamentale de la force du cylindre est la suivante
F = P × A
Où ?
- F = Force produite (N)
- P = Pression (Pa)
- A = Surface effective du piston (m²)
Considérations relatives à la surface effective
La zone d'action varie en fonction du type de cylindre et de la direction :
| Type de cylindre | Force d'extension | Force de rétraction |
|---|---|---|
| Simple effet | P × A | Force du ressort uniquement |
| Double effet (standard) | P × A | P × (A - a) |
| Double effet (sans tige) | P × A | P × A |
Où ?
- A = Surface totale du piston
- a = Surface de la section transversale de la tige
J'ai un jour consulté une usine de fabrication de l'Ohio qui ne disposait pas d'une force suffisante dans son application de pressage. Leurs calculs semblaient corrects sur le papier, mais les performances réelles laissaient à désirer. Après enquête, j'ai découvert qu'ils utilisaient pression manométrique2 dans leurs calculs au lieu de la pression absolue, et ils n'avaient pas tenu compte de la surface de la tige pendant la rétraction. Après avoir recalculé avec la formule et les valeurs de pression correctes, nous avons pu dimensionner correctement leur système, ce qui a permis d'augmenter la productivité de 23%.
Exemples pratiques de calcul de force
Examinons quelques calculs concrets :
Exemple 1 : Force d'extension dans un cylindre standard
Pour un cylindre avec :
- Diamètre de l'alésage = 50 mm (rayon = 25 mm = 0,025 m)
- Pression de service = 6 bar (600 000 Pa)
La zone du piston est :
A = π × r² = π × (0,025)² = 0,001963 m²
La force d'extension est :
F = P × A = 600 000 Pa × 0,001963 m² = 1 178 N ≈ 118 kg de force
Exemple 2 : Force de rétraction dans le même cylindre
Si le diamètre de la tige est de 20 mm (rayon = 10 mm = 0,01 m) :
La zone du bâton est :
a = π × r² = π × (0,01)² = 0,000314 m²
La zone de rétraction effective est :
A - a = 0,001963 - 0,000314 = 0,001649 m²
La force de rétractation est de :
F = P × (A - a) = 600 000 Pa × 0,001649 m² = 989 N ≈ 99 kg de force
Facteurs d'efficacité dans les applications réelles
Dans les applications pratiques, plusieurs facteurs affectent le calcul de la force théorique :
Pertes par frottement
Le frottement entre le joint du piston et la paroi du cylindre réduit la force effective :
| Type de joint | Facteur d'efficacité typique |
|---|---|
| Standard NBR | 0.85-0.90 |
| PTFE à faible friction | 0.90-0.95 |
| Joints vieillis/usés | 0.70-0.85 |
Equation de force pratique
L'équation de la force du monde réel est plus précise :
F_actual = η × P × A
Où ?
- η (eta) = Facteur d'efficacité (généralement 0,85-0,95)
Quelle est la relation entre le débit d'air et la pression dans les cylindres ?
La compréhension de la relation entre le débit et la pression est cruciale pour le dimensionnement des systèmes d'alimentation en air et la prévision de la vitesse de rotation des vérins.
Dans les systèmes pneumatiques, le débit d'air et la pression sont inversement proportionnels : plus la pression augmente, plus le débit diminue. Cette relation suit les lois des gaz et est affectée par les restrictions, la température et le volume du système. Pour que le vérin fonctionne correctement, il faut équilibrer ces facteurs afin d'obtenir la vitesse et la force souhaitées.
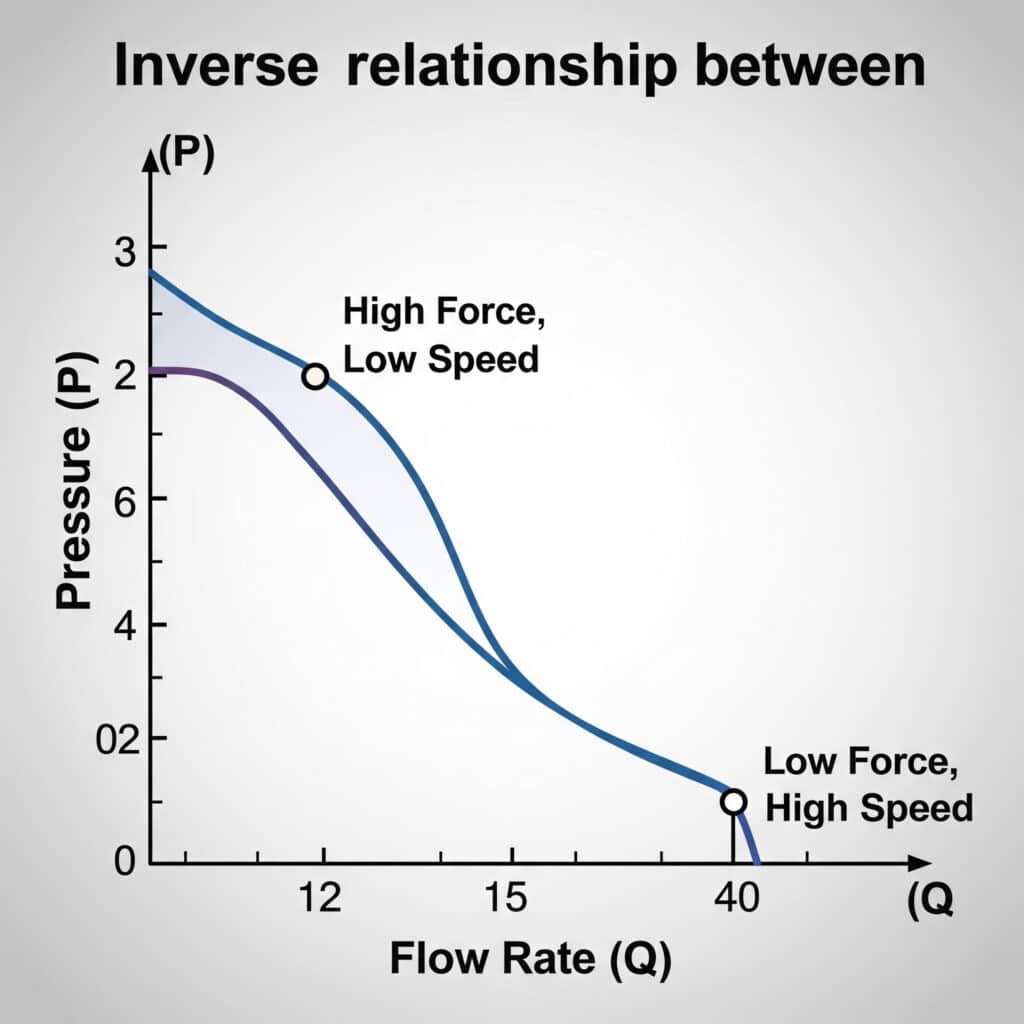
Tableau de conversion débit-pression
Ce tableau de référence pratique montre la relation entre le débit et la perte de charge dans divers composants du système :
| Taille du tuyau (mm) | Débit (l/min) | Perte de charge (bar/mètre) à 6 bar d'alimentation |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Les mathématiques de l'écoulement et de la pression
La relation entre le débit et la pression suit plusieurs lois sur les gaz :
Equation de Poiseuille3 pour l'écoulement laminaire
Pour un écoulement laminaire dans les tuyaux :
Q = (π × r⁴ × ΔP) / (8 × η × L)
Où ?
- Q = Débit volumétrique
- r = Rayon du tube
- ΔP = Différence de pression
- η = Viscosité dynamique
- L = Longueur du tube
Coefficient d'écoulement (Cv)4 Méthode
Pour les composants tels que les valves :
Q = Cv × √ΔP
Où ?
- Q = Débit
- Cv = Coefficient de débit
- ΔP = Perte de charge dans le composant
Calcul de la vitesse de rotation des cylindres
La vitesse d'un cylindre pneumatique dépend du débit et de la surface du cylindre :
v = Q / A
Où ?
- v = Vitesse du cylindre (m/s)
- Q = Débit (m³/s)
- A = Surface du piston (m²)
Au cours d'un projet récent dans une usine d'emballage en France, j'ai rencontré une situation où les cylindres sans tige du client se déplaçaient trop lentement malgré une pression adéquate. En analysant leur système à l'aide de nos calculs de débit et de pression, nous avons identifié des conduites d'alimentation sous-dimensionnées causant une chute de pression significative. Après être passé d'un tube de 6 mm à un tube de 10 mm, le temps de cycle a été amélioré de 40%, ce qui a permis d'augmenter considérablement la capacité de production.
Considérations critiques sur le débit
Plusieurs facteurs influencent la relation débit-pression dans les systèmes pneumatiques :
Phénomène d'écoulement étouffé5
Lorsque le rapport de pression dépasse une valeur critique (environ 0,53 pour l'air), le débit devient "étouffé" et ne peut plus augmenter, quelle que soit la réduction de pression en aval.
Effets de la température
Le débit est affecté par la température selon la relation suivante :
Q₂ = Q₁ × √(T₂/T₁)
Où ?
- Q₁, Q₂ = Débits à différentes températures
- T₁, T₂ = Températures absolues
Pourquoi la compréhension de la conversion des unités de pression est-elle essentielle pour la conception des systèmes ?
Il est essentiel de connaître les différentes unités de pression utilisées dans le monde pour concevoir correctement les systèmes et assurer leur compatibilité internationale.
La conversion des unités de pression est essentielle car les composants pneumatiques et les spécifications utilisent des unités différentes selon la région et l'industrie. Une mauvaise interprétation des unités peut entraîner des erreurs de calcul importantes, avec des conséquences potentiellement dangereuses. La conversion entre la pression absolue, la pression manométrique et la pression différentielle ajoute encore à la complexité.
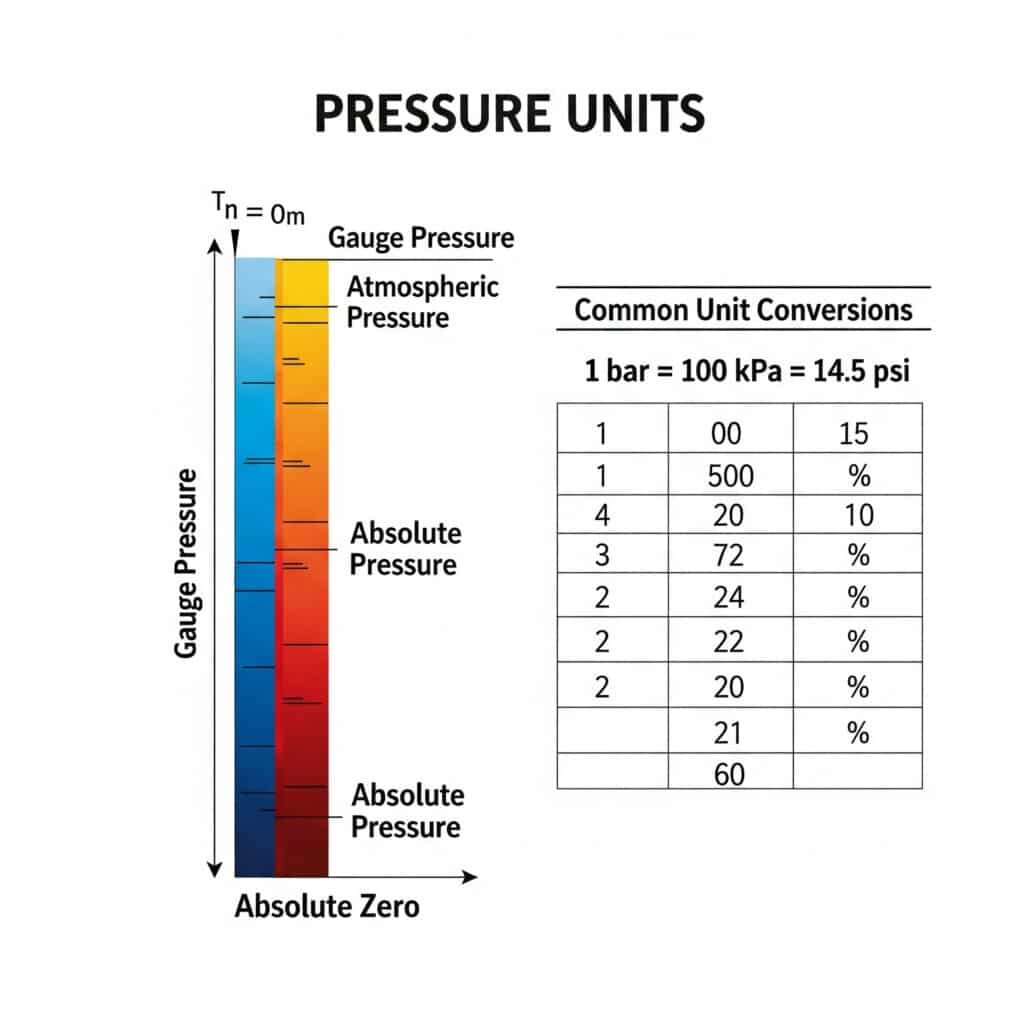
Guide de conversion des unités de pression absolue
Cette table de conversion complète permet de s'y retrouver dans les différentes unités de pression utilisées dans le monde :
| Unité | Symbole | Équivalent en Pa | Équivalent en bar | Équivalent en psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Barre | bar | 1 × 10⁵ | 1 | 14.5038 |
| Livre par pouce carré | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogramme-force par cm carré | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Mégapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmosphère | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Millimètre de mercure | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Pouce d'eau | enH₂O | 249.089 | 0.00249089 | 0.0361274 |
Pression absolue par rapport à la pression manométrique
Il est fondamental de comprendre la différence entre la pression absolue et la pression manométrique :
Calculateur de conversion de pression
Convertisseur d'unités de pression
Convertisseur de débit des cylindres
Formules de conversion
- P_absolu = P_gauge + P_atmosphérique
- P_gauge = P_absolu - P_atmosphérique
Lorsque la pression atmosphérique standard est d'environ :
- 1,01325 bar
- 14,7 psi
- 101 325 Pa
J'ai travaillé un jour avec une équipe d'ingénieurs en Allemagne qui avait acheté nos vérins sans tige mais qui signalait qu'ils n'atteignaient pas la force attendue. Après quelques recherches, nous avons découvert qu'ils utilisaient nos tableaux de force (basés sur la pression manométrique) mais qu'ils saisissaient des valeurs de pression absolue. Ce simple malentendu était à l'origine d'une erreur de calcul de 1 bar dans leurs attentes en matière de force. Après avoir clarifié la référence de pression, le système a fonctionné exactement comme prévu.
Exemples pratiques de conversion
Examinons quelques scénarios de conversion courants :
Exemple 1 : Conversion de la pression de travail d'une unité à l'autre
Une bouteille dont la pression de service maximale est de 0,7 MPa :
En bar :
0,7 MPa × 10 bar/MPa = 7 bar
En psi :
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Exemple 2 : Conversion de la pression manométrique en pression absolue
Un système fonctionnant à une pression de 6 bars :
En pression absolue (bar) :
6 bar_gauge + 1,01325 bar_atmosphérique = 7,01325 bar_absolu
Exemple 3 : Conversion de kgf/cm² en MPa
Un cylindre japonais spécifié pour 7 kgf/cm² :
En MPa :
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Préférences régionales en matière d'unités de pression
Les différentes régions utilisent généralement des unités de pression différentes :
| Région | Unités de pression courantes |
|---|---|
| Amérique du Nord | psi, inHg, inH₂O |
| L'Europe | bar, Pa, mbar |
| Japon | kgf/cm², MPa |
| Chine | MPa, bar |
| ROYAUME-UNI | bar, psi, Pa |
Mesure de la pression dans la documentation
Lorsqu'on documente les spécifications de pression, il est essentiel de les indiquer clairement :
- La valeur numérique
- L'unité de mesure
- Qu'il s'agisse de la pression manométrique (g) ou de la pression absolue (a)
Par exemple :
- 6 bar_g (pression manométrique, 6 bar au-dessus de l'atmosphère)
- 7,01 bar_a (pression absolue, pression totale y compris atmosphérique)
Conclusion
Comprendre la physique des vérins pneumatiques - des calculs de force de la loi de Pascal aux relations débit-pression et aux conversions d'unités de pression - est essentiel pour une conception et un dépannage corrects des systèmes. Ces principes fondamentaux permettent de s'assurer que vos systèmes pneumatiques fournissent les performances attendues de manière fiable et efficace.
FAQ sur la physique des systèmes pneumatiques
Comment calculer la force de sortie d'un vérin pneumatique sans tige ?
Pour calculer la force produite par un vérin pneumatique sans tige, il faut multiplier la pression de fonctionnement par la surface effective du piston (F = P × A). Par exemple, un vérin sans tige avec un alésage de 50 mm (0,001963 m² de surface) fonctionnant à 6 bars (600 000 Pa) produira environ 1 178 N de force. Contrairement aux vérins traditionnels, les vérins sans tige ont généralement la même surface effective dans les deux sens.
Comment calculer la force de sortie d'un vérin pneumatique sans tige ?
Pour calculer la force produite par un vérin pneumatique sans tige, il faut multiplier la pression de fonctionnement par la surface effective du piston (F = P × A). Par exemple, un vérin sans tige avec un alésage de 50 mm (0,001963 m² de surface) fonctionnant à 6 bars (600 000 Pa) produira environ 1 178 N de force. Contrairement aux vérins traditionnels, les vérins sans tige ont généralement la même surface effective dans les deux sens.
Quelle est la différence entre la pression manométrique et la pression absolue ?
La pression manométrique (bar_g, psi_g) mesure la pression par rapport à la pression atmosphérique, la pression atmosphérique étant égale à zéro. La pression absolue (bar_a, psi_a) mesure la pression par rapport à un vide parfait, qui est égal à zéro. Pour passer de la pression manométrique à la pression absolue, il faut ajouter la pression atmosphérique (environ 1,01325 bar ou 14,7 psi) à la valeur mesurée par le manomètre.
Comment le débit d'air affecte-t-il la vitesse du cylindre ?
La vitesse du vérin est directement proportionnelle au débit d'air et inversement proportionnelle à la surface du piston (v = Q/A). Un débit insuffisant dû à des conduites d'alimentation sous-dimensionnées, à des raccords restrictifs ou à des soupapes inadéquates limitera la vitesse de la bouteille, quelle que soit la pression. Par exemple, un débit de 20 litres/seconde dans un vérin dont le piston a une surface de 0,002 m² produira une vitesse de 10 mètres/seconde.
Pourquoi les cylindres pneumatiques se déplacent-ils parfois plus lentement que prévu ?
Les vérins pneumatiques peuvent se déplacer plus lentement que prévu en raison de plusieurs facteurs : restrictions de l'alimentation en air entraînant des chutes de pression, frottement interne des joints, charges mécaniques dépassant les calculs, fuites réduisant la pression effective ou effets de la température sur la densité de l'air. En outre, les coefficients de débit des vannes limitent souvent le débit réel disponible pour le vérin.
Comment convertir les différentes unités de pression pour les spécifications internationales ?
Pour passer d'une unité de pression à une autre, il faut utiliser des facteurs de multiplication : 1 bar = 100 000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Vérifiez toujours si la pression est spécifiée comme étant relative ou absolue, car cette distinction peut affecter les calculs de manière significative. Par exemple, 6 bar_g équivaut à 7,01325 bar_a dans des conditions atmosphériques standard.
Quelle est la relation entre la taille de l'alésage du cylindre et la force produite ?
La relation entre la taille de l'alésage du vérin et la force produite est quadratique : en doublant le diamètre de l'alésage, on multiplie par quatre la force produite (puisque la surface = π × r²). Par exemple, à une pression de fonctionnement de 6 bars, un vérin de 40 mm d'alésage produit une force d'environ 754 N, tandis qu'un vérin de 80 mm d'alésage produit une force d'environ 3 016 N, soit près de quatre fois plus.
-
Explique en détail la loi de Pascal, un principe fondamental de la mécanique des fluides qui est à la base de la transmission de puissance hydraulique et pneumatique. ↩
-
Offre une définition claire et une comparaison de la pression manométrique et de la pression absolue, une distinction essentielle pour des calculs techniques précis car la pression manométrique est relative à la pression atmosphérique. ↩
-
Explique la dérivation et l'application de la loi de Poiseuille, qui décrit la perte de charge d'un fluide incompressible et newtonien s'écoulant dans une longue conduite cylindrique en régime laminaire. ↩
-
Fournit une définition technique du coefficient de débit (Cv), une mesure impériale qui fournit un moyen normalisé de comparer les capacités de débit de différentes vannes. ↩
-
Détaille la physique de l'écoulement étranglé, une condition de la dynamique des fluides qui limite le débit massique d'un fluide compressible à travers une restriction lorsque la vitesse atteint la vitesse du son. ↩


