
Avete mai toccato un cilindro pneumatico dopo un funzionamento continuo e siete rimasti sorpresi dalla sensazione di calore? Quel calore non è solo un inconveniente: rappresenta uno spreco di energia, una riduzione dell'efficienza e potenziali problemi di affidabilità che potrebbero costare migliaia di euro alla vostra azienda.
Il trasferimento di calore nei sistemi pneumatici avviene attraverso tre meccanismi: conduzione attraverso i materiali dei componenti, convezione tra le superfici e l'aria e irraggiamento dalle superfici calde. La comprensione e l'ottimizzazione di questi principi può ridurre le temperature di esercizio di 15-30%, prolungare la vita dei componenti fino a 40% e migliorare l'efficienza energetica di 5-15%.
Il mese scorso ho prestato consulenza a uno stabilimento di trasformazione alimentare in Georgia, dove i cilindri senza stelo si guastavano ogni 3-4 mesi a causa di problemi termici. Il team di manutenzione si limitava a sostituire i componenti senza affrontare la causa principale. Applicando i corretti principi di trasferimento del calore, abbiamo ridotto le temperature di esercizio di 22°C e allungato la vita dei componenti a oltre un anno. Lasciate che vi mostri come abbiamo fatto e come potete applicare questi stessi principi ai vostri sistemi.
Indice dei contenuti
- Calcolo del coefficiente di conduzione: Come si muove il calore attraverso i componenti?
- Metodi di miglioramento della convezione: Quali tecniche massimizzano il trasferimento di calore aria-superficie?
- Modello di efficienza radiativa: Quando è importante l'irraggiamento termico nei sistemi pneumatici?
- Conclusione
- Domande frequenti sul trasferimento di calore nei sistemi pneumatici
Calcolo del coefficiente di conduzione: Come si muove il calore attraverso i componenti?
La conduzione è il principale meccanismo di trasferimento del calore nei componenti pneumatici solidi. Capire come calcolare e ottimizzare i coefficienti di conduzione è essenziale per gestire le temperature del sistema.
Il coefficiente di conduzione del calore può essere calcolato con il seguente metodo Legge di Fourier1: q = -k(dT/dx), dove q è il flusso di calore (W/m²), k è la conduttività termica (W/m-K) e dT/dx è il gradiente di temperatura. Per i componenti pneumatici, la conduzione efficace dipende dalla scelta del materiale, dalla qualità dell'interfaccia e da fattori geometrici che influenzano la lunghezza del percorso termico e l'area della sezione trasversale.
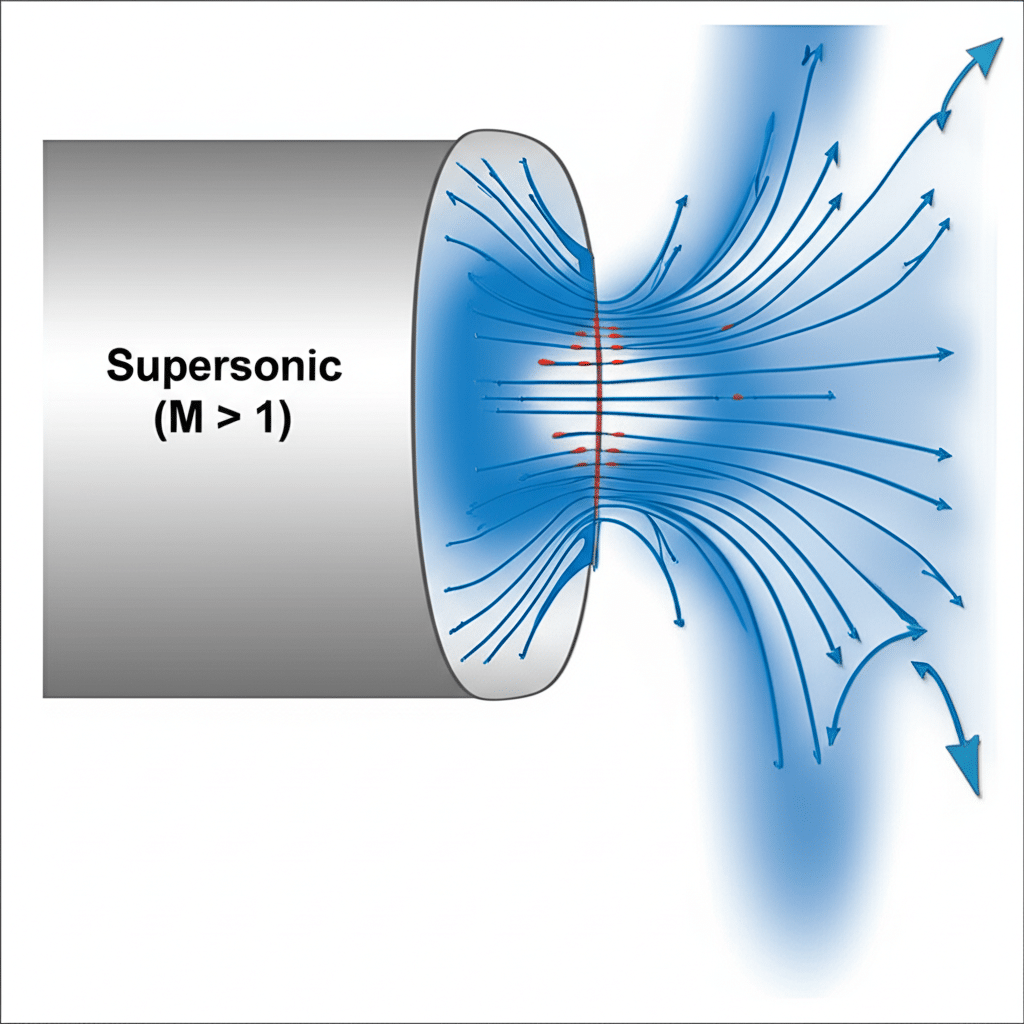
Ricordo la risoluzione dei problemi di una linea di produzione in Tennessee in cui i cuscinetti dei cilindri senza stelo si guastavano prematuramente. Il team di manutenzione aveva provato diversi lubrificanti senza successo. Quando abbiamo analizzato i percorsi di conduzione, abbiamo scoperto un collo di bottiglia termico all'interfaccia cuscinetto-alloggiamento. Migliorando la finitura superficiale e applicando un composto termoconduttivo, abbiamo aumentato il coefficiente di conduzione effettivo di 340% ed eliminato completamente i guasti.
Equazioni fondamentali della conduzione
Vediamo le equazioni chiave per il calcolo della conduzione nei componenti pneumatici:
Legge di Fourier per la conduzione del calore
L'equazione di base che regola la conduzione del calore è:
q = -k(dT/dx)
Dove:
- q = Flusso di calore (W/m²)
- k = Conduttività termica (W/m-K)
- dT/dx = gradiente di temperatura (K/m)
Per un semplice caso monodimensionale a sezione costante:
Q = kA(T₁-T₂)/L
Dove:
- Q = Velocità di trasferimento del calore (W)
- A = Area della sezione trasversale (m²)
- T₁, T₂ = Temperature a ciascuna estremità (K)
- L = Lunghezza del percorso termico (m)
Concetto di resistenza termica
Per le geometrie complesse, l'approccio della resistenza termica è spesso più pratico:
R = L/(kA)
Dove:
- R = Resistenza termica (K/W)
Per i sistemi con più componenti in serie:
Rtotale = R₁ + R₂ + R₃ + ... + Rₙ
E la velocità di trasferimento del calore diventa:
Q = ΔT/Rtotale
Confronto della conducibilità termica dei materiali
| Materiale | Conduttività termica (W/m-K) | Conduttività relativa | Applicazioni comuni |
|---|---|---|---|
| Alluminio | 205-250 | Alto | Cilindri, dissipatori di calore |
| Acciaio | 36-54 | Medio | Componenti strutturali |
| Acciaio inox | 14-16 | Medio-basso | Ambienti corrosivi |
| Bronzo | 26-50 | Medio | Cuscinetti, boccole |
| PTFE | 0.25 | Molto basso | Guarnizioni, cuscinetti |
| Gomma nitrilica | 0.13 | Molto basso | O-ring, guarnizioni |
| Aria (ferma) | 0.026 | Estremamente basso | Riempimento delle lacune |
| Pasta termica | 3-8 | Basso | Materiale dell'interfaccia |
Resistenza di contatto nei gruppi pneumatici
Nelle interfacce tra i componenti, la resistenza di contatto influisce in modo significativo sul trasferimento di calore:
Rcontatto = 1/(hc × A)
Dove:
- hc = coefficiente di contatto (W/m²-K)
- A = Area di contatto (m²)
I fattori che influenzano la resistenza di contatto includono:
- Ruvidità della superficie: Le superfici più ruvide hanno una minore area di contatto effettiva
- Contatto Pressione: Una pressione più elevata aumenta l'area di contatto effettiva
- Materiali di interfaccia: I composti termici riempiono i vuoti d'aria
- Pulizia delle superfici: I contaminanti possono aumentare la resistenza
Caso di studio: Ottimizzazione termica del cilindro senza stelo
Per un cilindro magnetico senza stelo che presenta problemi termici:
| Componente | Design originale | Design ottimizzato | Miglioramento |
|---|---|---|---|
| Corpo cilindro | Alluminio anodizzato | Stesso materiale, finitura migliorata | 15% migliore conduzione |
| Interfaccia del cuscinetto | Contatto metallo-metallo | Composto termico aggiunto | 340% migliore conduzione |
| Staffe di montaggio | Acciaio verniciato | Alluminio nudo | 280% migliore conduzione |
| Resistenza termica complessiva | 2,8 K/W | 0,7 K/W | Riduzione 75% |
| Temperatura di esercizio | 78°C | 56°C | Riduzione di 22°C |
| Vita del componente | 4 mesi | >12 mesi | Miglioramento 3× |
Tecniche pratiche di ottimizzazione della conduzione
Sulla base della mia esperienza con centinaia di sistemi pneumatici, ecco gli approcci più efficaci per migliorare la conduzione:
Ottimizzazione dell'interfaccia
- Finitura delle superfici: Migliorare la levigatezza della superficie di accoppiamento a Ra 0,4-0,8 μm
- Materiali per l'interfaccia termica2: Applicare composti appropriati (3-8 W/m-K)
- Coppia di serraggio: Assicurare il corretto serraggio per una pressione di contatto ottimale
- Pulizia: Rimuovere tutti gli oli e i contaminanti prima del montaggio
Strategie di selezione dei materiali
- Percorsi termici critici: Utilizzare materiali ad alta conduttività (alluminio, rame).
- Interruzioni termiche: Utilizzare intenzionalmente materiali a bassa conduttività per isolare il calore.
- Approcci compositi: Combinare i materiali per ottenere prestazioni/costi ottimali
- Materiali anisotropi: Utilizzare la conduttività direzionale, ove opportuno
Ottimizzazione geometrica
- Lunghezza del percorso termico: Ridurre al minimo la distanza tra le fonti di calore e i dissipatori di calore.
- Area trasversale: Massimizzare l'area perpendicolare al flusso di calore
- Colli di bottiglia termici: Identificare ed eliminare le strozzature nel percorso del calore.
- Percorsi ridondanti: Creare più percorsi di conduzione paralleli
Metodi di miglioramento della convezione: Quali tecniche massimizzano il trasferimento di calore aria-superficie?
La convezione è spesso il fattore limitante nel raffreddamento dei sistemi pneumatici. Il miglioramento del trasferimento di calore convettivo può migliorare notevolmente la gestione termica e le prestazioni del sistema.
Il trasferimento di calore convettivo segue Legge di Newton sul raffreddamento3: Q = hA(Ts-T∞), dove h è il coefficiente di convezione (W/m²-K), A è l'area della superficie e (Ts-T∞) è la differenza di temperatura tra la superficie e il fluido. I metodi di miglioramento includono l'aumento dell'area superficiale attraverso le alette, il miglioramento della velocità del fluido con un flusso d'aria diretto e l'ottimizzazione delle caratteristiche della superficie per promuovere strati limite turbolenti.
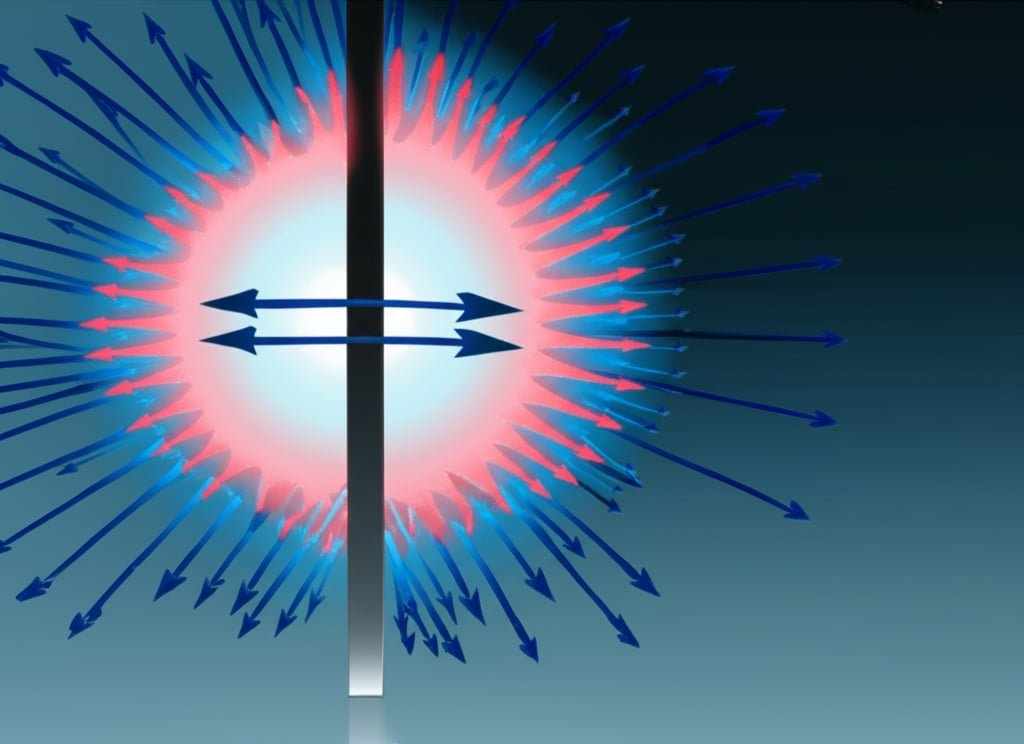
Durante una verifica dell'efficienza energetica presso un impianto di confezionamento in Arizona, mi sono imbattuto in un sistema pneumatico che operava in un ambiente a 43°C. I cilindri senza stelo si surriscaldavano nonostante i requisiti di manutenzione. I cilindri senza stelo si surriscaldavano nonostante rispettassero tutti i requisiti di manutenzione. Implementando un miglioramento mirato della convezione - aggiungendo piccole alette di alluminio e una ventola a basso consumo - abbiamo aumentato il coefficiente di convezione di 450%. In questo modo abbiamo ridotto le temperature di esercizio da livelli pericolosi a livelli conformi alle specifiche, senza apportare modifiche sostanziali al sistema.
Fondamenti del trasferimento di calore per convezione
L'equazione di base che regola il trasferimento di calore convettivo è:
Q = hA(Ts-T∞)
Dove:
- Q = Velocità di trasferimento del calore (W)
- h = coefficiente di convezione (W/m²-K)
- A = Superficie (m²)
- Ts = Temperatura superficiale (K)
- T∞ = Temperatura del fluido (aria) (K)
Il coefficiente di convezione h dipende da molteplici fattori:
- Proprietà del fluido (densità, viscosità, conduttività termica)
- Caratteristiche del flusso (velocità, turbolenza)
- Geometria e orientamento della superficie
- Regime di flusso (convezione naturale o forzata)
Convezione naturale contro convezione forzata
| Parametro | Convezione naturale | Convezione forzata | Implicazioni |
|---|---|---|---|
| Valore h tipico | 5-25 W/m²-K | 25-250 W/m²-K | La convezione forzata può essere 10 volte più efficace |
| Forza motrice | Galleggiamento (differenza di temperatura) | Pressione esterna (ventilatori, soffianti) | La convezione forzata è meno dipendente dalla temperatura |
| Schema di flusso | Flusso verticale lungo le superfici | Direzionale in base al meccanismo di forzatura | Il flusso forzato può essere ottimizzato per componenti specifici |
| Affidabilità | Passivo, sempre presente | Richiede alimentazione e manutenzione | La convezione naturale fornisce un raffreddamento di base |
| Requisiti di spazio | Richiede spazio per la circolazione dell'aria | Richiede spazio per i ventilatori e le condutture. | I sistemi forzati richiedono una maggiore pianificazione |
Tecniche di miglioramento della convezione
Aumento della superficie
Aumento della superficie effettiva attraverso:
Pinne e superfici estese
- Alette a spillo: Flusso d'aria omnidirezionale, aumento dell'area di 150-300%
- Alette a piastra: Flusso d'aria direzionale, aumento dell'area di 200-500%
- Superfici ondulate: Miglioramento moderato, aumento dell'area 50-150%Irruvidimento della superficie
- Microtesturizzazione: 5-15% aumento dell'area effettiva
- Superfici a lamelle: aumento di 10-30% più effetti di strato limite
- Modelli scanalati: 15-40% aumentano con vantaggi direzionali
Manipolazione del flusso
Miglioramento delle caratteristiche del flusso d'aria attraverso:
Sistemi ad aria forzata
- Ventilatori: flusso d'aria direzionale, miglioramento 200-600% h
- Soffiatori: Flusso ad alta pressione, miglioramento 300-800% h
- Getti di aria compressa: Raffreddamento mirato, 400-1000% miglioramento locale hOttimizzazione del percorso del flusso
- Baffles: Dirigono l'aria verso i componenti critici
- Effetti Venturi: Accelerano l'aria su superfici specifiche
- Generatori di vortici: Creano turbolenza per l'interruzione dello strato limite
Modifiche della superficie
Alterare le proprietà della superficie per migliorare la convezione:
Trattamenti emissivi
- Ossido nero: Aumenta l'emissività a 0,7-0,9
- Anodizzazione: Emissività controllata da 0,4-0,9
- Vernici e rivestimenti: Emissività personalizzabile fino a 0,98Controllo della bagnabilità
- Rivestimenti idrofili: Migliorano il raffreddamento dei liquidi
- Superfici idrofobe: Prevengono i problemi di condensa
- Bagnabilità modellata: Flusso diretto di condensa
Esempio pratico di implementazione
Per un cilindro pneumatico senza stelo che opera in un ambiente ad alta temperatura:
| Metodo di potenziamento | Attuazione | h Miglioramento | Riduzione della temperatura |
|---|---|---|---|
| Alette a spillo (6 mm) | Alette a clip in alluminio, spaziatura di 10 mm | 180% | 12°C |
| Flusso d'aria diretto | Ventola da 80 mm, 2 W CC a 1,5 m/s | 320% | 18°C |
| Trattamento della superficie | Anodizzazione nera | 40% | 3°C |
| Approccio combinato | Tutti i metodi integrati | 450% | 24°C |
Correlazione del numero di Nusselt per i calcoli di progetto
Per i calcoli ingegneristici, il Numero di Nusselt4 (Nu) fornisce un approccio dimensionale alla convezione:
Nu = hL/k
Dove:
- L = Lunghezza caratteristica
- k = Conducibilità termica del fluido
Per la convezione forzata su una piastra piana:
Nu = 0,664Re^(1/2)Pr^(1/3) (flusso laminare)
Nu = 0,037Re^(4/5)Pr^(1/3) (flusso turbolento)
Dove:
- Re = numero di Reynolds (velocità × lunghezza × densità / viscosità)
- Pr = numero di Prandtl (calore specifico × viscosità / conducibilità termica)
Queste correlazioni consentono agli ingegneri di prevedere i coefficienti di convezione per diverse configurazioni e di ottimizzare di conseguenza le strategie di raffreddamento.
Modello di efficienza radiativa: Quando è importante l'irraggiamento termico nei sistemi pneumatici?
La radiazione è spesso trascurata nella gestione termica dei sistemi pneumatici, ma può rappresentare 15-30% del trasferimento di calore totale in molte applicazioni. Capire quando e come ottimizzare il trasferimento di calore radiativo è fondamentale per una gestione termica completa.
Il trasferimento di calore per irraggiamento segue la Legge di Stefan-Boltzmann5: Q = εσA(T₁⁴-T₂⁴), dove ε è l'emissività della superficie, σ è la costante di Stefan-Boltzmann, A è l'area della superficie e T₁ e T₂ sono le temperature assolute della superficie emittente e dell'ambiente circostante. L'efficienza di irraggiamento nei sistemi pneumatici dipende principalmente dall'emissività della superficie, dal differenziale di temperatura e dai fattori di vista tra i componenti e l'ambiente circostante.
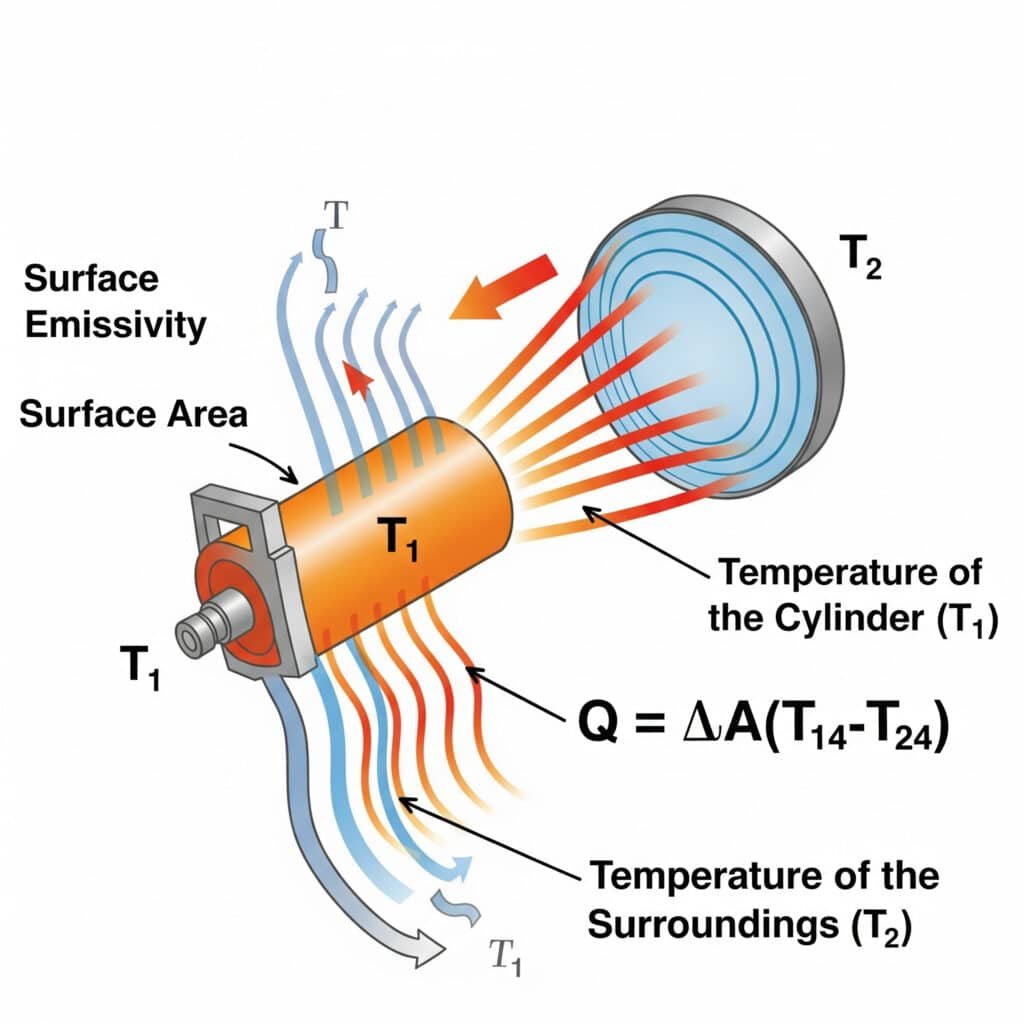
Di recente ho aiutato un produttore di apparecchiature per semiconduttori dell'Oregon a risolvere i problemi di surriscaldamento dei suoi cilindri di precisione senza stelo. I loro ingegneri si erano concentrati esclusivamente sulla conduzione e sulla convezione, trascurando la radiazione. Applicando un rivestimento ad alta emissività (aumentando ε da 0,11 a 0,92), abbiamo migliorato il trasferimento di calore radiativo di oltre 700%. Questa soluzione semplice e passiva ha ridotto le temperature di esercizio di 9°C senza parti in movimento o consumo di energia, un requisito fondamentale per l'ambiente della camera bianca.
Fondamenti di trasferimento del calore per irraggiamento
L'equazione di base che regola il trasferimento di calore per via radiativa è:
Q = εσA(T₁⁴-T₂⁴)
Dove:
- Q = Velocità di trasferimento del calore (W)
- ε = Emissività (adimensionale, 0-1)
- σ = costante di Stefan-Boltzmann (5,67 × 10-⁸ W/m²-K⁴)
- A = Superficie (m²)
- T₁ = Temperatura assoluta della superficie (K)
- T₂ = Temperatura assoluta circostante (K)
Valori di emissività superficiale per i materiali pneumatici più comuni
| Materiale/Superficie | Emissività (ε) | Efficienza di radiazione | Potenziale di potenziamento |
|---|---|---|---|
| Alluminio lucidato | 0.04-0.06 | Molto scarso | >1500% miglioramento possibile |
| Alluminio anodizzato | 0.7-0.9 | Eccellente | Già ottimizzato |
| Acciaio inox (lucido) | 0.07-0.14 | Povero | Possibile miglioramento >600% |
| Acciaio inox (ossidato) | 0.6-0.85 | Buono | Possibile un miglioramento moderato |
| Acciaio (lucido) | 0.07-0.10 | Povero | >900% miglioramento possibile |
| Acciaio (ossidato) | 0.7-0.9 | Eccellente | Già ottimizzato |
| Superfici verniciate | 0.8-0.98 | Eccellente | Già ottimizzato |
| PTFE (bianco) | 0.8-0.9 | Eccellente | Già ottimizzato |
| Gomma nitrilica | 0.86-0.94 | Eccellente | Già ottimizzato |
Considerazioni sul fattore di vista
Lo scambio di radiazioni non dipende solo dall'emissività, ma anche dalle relazioni geometriche tra le superfici:
F₁₂ = frazione di radiazione che lascia la superficie 1 e colpisce la superficie 2
Per le geometrie complesse, i fattori di vista possono essere calcolati utilizzando:
- Soluzioni analitiche per geometrie semplici
- Visualizza l'algebra dei fattori per la combinazione di soluzioni note
- Metodi numerici per disposizioni complesse
- Approssimazioni empiriche per l'ingegneria pratica
Dipendenza dalla temperatura della radiazione
La relazione di quarta potenza della temperatura rende l'irraggiamento particolarmente efficace alle temperature più elevate:
| Temperatura di superficie | Percentuale di trasferimento di calore per irraggiamento* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Supponendo condizioni di convezione naturale, ε = 0,8, 25°C ambiente
Strategie di miglioramento dell'efficienza di radiazione
Sulla base della mia esperienza con i sistemi pneumatici industriali, ecco gli approcci più efficaci per migliorare il trasferimento di calore per irraggiamento:
Modifica dell'emissività della superficie
Rivestimenti ad alta emissività
- Anodizzazione nera per alluminio (ε ≈ 0,8-0,9)
- Ossido nero per acciaio (ε ≈ 0,7-0,8)
- Rivestimenti ceramici speciali (ε ≈ 0,9-0,98)Texture della superficie
- La micro-ruvidità aumenta l'emissività effettiva
- Le superfici porose migliorano le proprietà radiative
- Miglioramenti combinati di emissività/convezione
Ottimizzazione ambientale
Gestione della temperatura circostante
- Schermatura da apparecchiature/processi caldi
- Pareti/soffitti freddi per un migliore scambio di radiazioni
- Barriere riflettenti per indirizzare la radiazione verso superfici più fredde.Visualizza il miglioramento del fattore
- Orientamento per massimizzare l'esposizione alle superfici fredde
- Rimozione di oggetti bloccanti
- Riflettori per migliorare lo scambio di radiazioni con le aree più fredde
Caso di studio: Miglioramento delle radiazioni nella pneumatica di precisione
Per un cilindro senza stelo di alta precisione in un ambiente di camera bianca:
| Parametro | Design originale | Design potenziato dalle radiazioni | Miglioramento |
|---|---|---|---|
| Materiale di superficie | Alluminio lucido (ε ≈ 0,06) | Alluminio rivestito in ceramica (ε ≈ 0,94) | 1467% aumento dell'emissività |
| Trasferimento di calore per irraggiamento | 2.1W | 32.7W | 1457% aumento della radiazione |
| Temperatura di esercizio | 68°C | 59°C | Riduzione di 9°C |
| Vita del componente | 8 mesi | >24 mesi | Miglioramento 3× |
| Costo di implementazione | – | $175 per cilindro | 4,2 mesi di ritorno dell'investimento |
Irradiazione e altre modalità di trasferimento del calore
Capire quando la radiazione domina è fondamentale per una gestione termica efficiente:
| Condizione | Dominanza della conduzione | Dominanza della convezione | Dominanza delle radiazioni |
|---|---|---|---|
| Intervallo di temperatura | Da basso ad alto | Da basso a medio | Medio-Alto |
| Proprietà del materiale | Materiali ad alto tenore di k | Basso k, elevata superficie | Superfici ε elevate |
| Fattori ambientali | Buon contatto termico | Aria in movimento, ventilatori | Ampio differenziale di temperatura |
| Vincoli di spazio | Imballaggio stretto | Flusso d'aria aperto | Vista sui dintorni più freschi |
| Le migliori applicazioni | Interfacce dei componenti | Raffreddamento generale | Superfici calde, vuoto, aria ferma |
Conclusione
La padronanza dei principi di trasferimento del calore - calcolo del coefficiente di conduzione, metodi di miglioramento della convezione e modellazione dell'efficienza di irraggiamento - fornisce le basi per una gestione termica efficace nei sistemi pneumatici. Applicando questi principi, è possibile ridurre le temperature di esercizio, prolungare la durata dei componenti e migliorare l'efficienza energetica, garantendo un funzionamento affidabile anche in ambienti difficili.
Domande frequenti sul trasferimento di calore nei sistemi pneumatici
Qual è l'aumento di temperatura tipico dei cilindri pneumatici durante il funzionamento?
I cilindri pneumatici subiscono in genere aumenti di temperatura di 20-40°C rispetto all'ambiente durante il funzionamento continuo. Questo aumento è dovuto all'attrito tra le guarnizioni e le pareti del cilindro, al riscaldamento dell'aria per compressione e alla conversione del lavoro meccanico in calore. I cilindri senza stelo subiscono spesso aumenti di temperatura più elevati (30-50°C) a causa dei sistemi di tenuta più complessi e della generazione di calore concentrata nel gruppo cuscinetto/guarnizione.
In che modo la pressione di esercizio influisce sulla generazione di calore nei sistemi pneumatici?
La pressione di esercizio ha un impatto significativo sulla generazione di calore: le pressioni più elevate generano più calore attraverso diversi meccanismi. Ogni aumento di 1 bar della pressione di esercizio aumenta in genere la generazione di calore di 8-12% a causa delle maggiori forze di attrito tra le guarnizioni e le superfici, del maggiore riscaldamento alla compressione e delle maggiori perdite dovute alle perdite. Questa relazione è approssimativamente lineare entro i normali intervalli di funzionamento (3-10 bar).
Qual è l'approccio di raffreddamento ottimale per i componenti pneumatici in diversi ambienti?
L'approccio ottimale al raffreddamento varia a seconda dell'ambiente: in ambienti puliti e a temperatura moderata (15-30°C), spesso è sufficiente la convezione naturale con un'adeguata spaziatura dei componenti. In ambienti ad alta temperatura (30-50°C), si rende necessaria la convezione forzata con ventole o aria compressa. In condizioni estremamente calde (>50°C) o dove il flusso d'aria è limitato, possono essere necessari metodi di raffreddamento attivo come i raffreddatori termoelettrici o il raffreddamento a liquido. In tutti i casi, la massimizzazione della radiazione attraverso superfici ad alta emissività fornisce un ulteriore raffreddamento passivo.
Come si calcola il trasferimento totale di calore da un componente pneumatico?
Calcolare il trasferimento di calore totale sommando i contributi di ciascun meccanismo: Qtotal = Qconduzione + Qconvezione + Qirraggiamento. Per la conduzione, utilizzare Q = kA(T₁-T₂)/L per ogni percorso termico. Per la convezione, utilizzare Q = hA(Ts-T∞) con i coefficienti di convezione appropriati. Per l'irraggiamento, utilizzare Q = εσA(T₁⁴-T₂⁴). Nella maggior parte delle applicazioni pneumatiche industriali che operano a 30-80°C, la distribuzione approssimativa è 20-40% per conduzione, 40-70% per convezione e 10-30% per irraggiamento.
Qual è il rapporto tra temperatura e durata dei componenti pneumatici?
La durata dei componenti diminuisce esponenzialmente con l'aumentare della temperatura, secondo una relazione di Arrhenius modificata. Come regola generale, ogni aumento di 10°C della temperatura di esercizio riduce la durata delle guarnizioni e dei componenti di 40-50%. Ciò significa che un componente funzionante a 70°C potrebbe durare solo un terzo della durata dello stesso componente a 50°C. Questa relazione è particolarmente critica per i componenti polimerici come le tenute, i cuscinetti e le guarnizioni, che spesso determinano l'intervallo di manutenzione dei sistemi pneumatici.
-
Fornisce una spiegazione fondamentale della Legge di Fourier, il principio fondamentale che descrive come il calore viene condotto attraverso i materiali solidi in base alla loro conducibilità termica e al gradiente di temperatura. ↩
-
Spiega la funzione e i tipi di materiali di interfaccia termica (TIM), utilizzati per riempire microscopici spazi d'aria tra i componenti per migliorare la conduzione del calore e ridurre la resistenza termica. ↩
-
Illustra i principi della legge di Newton sul raffreddamento, che regola il modo in cui gli oggetti si raffreddano trasferendo il calore al fluido circostante attraverso la convezione, un fattore chiave nella progettazione dei sistemi di raffreddamento. ↩
-
Offre uno sguardo approfondito sul numero di Nusselt, una grandezza adimensionale critica nella fluidodinamica e nel trasferimento di calore che rappresenta il rapporto tra il trasferimento di calore convettivo e quello conduttivo attraverso un confine. ↩
-
Descrive la legge di Stefan-Boltzmann, il principio fisico fondamentale che quantifica l'energia totale irradiata da un corpo nero, essenziale per calcolare la perdita di calore dalle superfici calde. ↩


