
Avete problemi di velocità incoerenti dei cilindri pneumatici o di impatti inaspettati a fine corsa? Questi problemi comuni derivano spesso da una scarsa conoscenza della cinematica del pistone. Molti ingegneri si concentrano esclusivamente sui requisiti di forza, trascurando i parametri di movimento critici che determinano le prestazioni del sistema.
Cinematica del pistone1 hanno un impatto diretto sulle prestazioni del sistema pneumatico attraverso le relazioni pressione-velocità, i limiti di accelerazione e i requisiti di ammortizzazione. La comprensione di questi principi consente agli ingegneri di dimensionare correttamente i componenti, prevedere i profili di movimento effettivi e prevenire guasti prematuri nei cilindri senza stelo e in altri attuatori pneumatici.
Negli oltre 15 anni trascorsi in Bepto a lavorare con i sistemi pneumatici, ho visto innumerevoli casi in cui la comprensione di questi principi fondamentali ha aiutato i clienti a risolvere problemi di prestazioni persistenti e a prolungare la durata delle apparecchiature di 3-5 volte.
Indice dei contenuti
- Quale pressione è effettivamente necessaria per il movimento a velocità costante?
- Come si calcola l'accelerazione massima possibile nei cilindri pneumatici?
- Perché il tempo di ammortizzazione è importante e come si calcola?
- Conclusione
- Domande frequenti sulla cinematica dei pistoni nei sistemi pneumatici
Quale pressione è effettivamente necessaria per il movimento a velocità costante?
Molti ingegneri si limitano ad applicare la massima pressione disponibile ai loro sistemi pneumatici, ma questo approccio è inefficiente e può portare a movimenti a scatti, usura eccessiva e spreco di energia.
La pressione necessaria per il movimento a velocità costante in un cilindro pneumatico si calcola con P = (F + Fr)/A, dove P è la pressione, F è la forza di carico esterna, Fr è la resistenza all'attrito e A è l'area del pistone. Questo calcolo garantisce un funzionamento fluido ed efficiente senza una pressione eccessiva che spreca energia e accelera l'usura dei componenti.
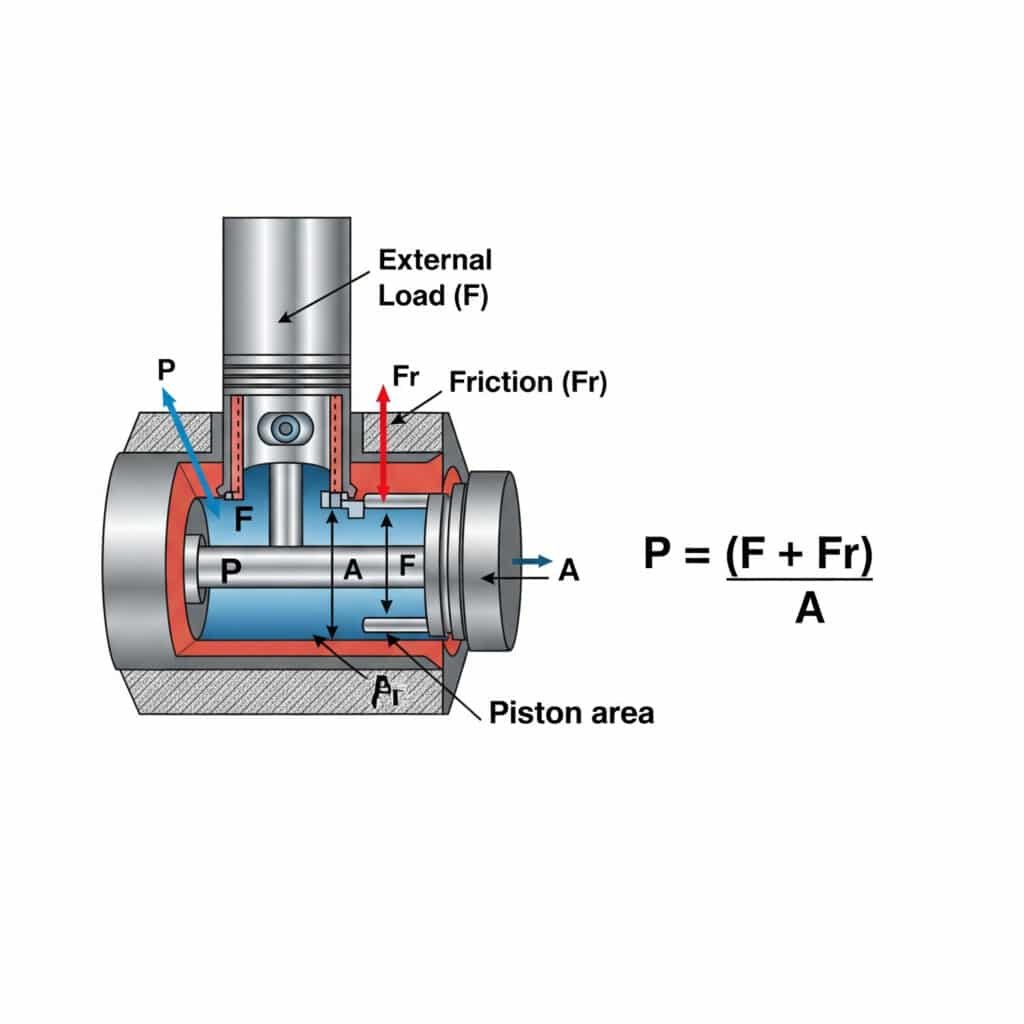
La comprensione dei requisiti di pressione per il movimento a velocità costante ha implicazioni pratiche per la progettazione e il funzionamento del sistema. Permettetemi di suddividere il tutto in informazioni utili per l'azione.
Fattori che influenzano i requisiti di pressione a velocità costante
La pressione necessaria per mantenere una velocità costante dipende da diversi fattori:
| Fattore | Impatto sul fabbisogno di pressione | Considerazioni pratiche |
|---|---|---|
| Carico esterno | Relazione lineare diretta | Varia in base all'orientamento e alle forze esterne |
| Attrito | Aumenta la pressione richiesta | Cambiamenti con l'usura delle guarnizioni e la lubrificazione |
| Area del pistone | Inversamente proporzionale | Foro più grande = minore pressione richiesta |
| Restrizioni alla fornitura di aria | Perdite di pressione nelle linee/valvole | Dimensionare i componenti per ridurre al minimo le perdite di carico |
| Contropressione | Contrario alla mozione | Considerare la capacità del flusso di scarico |
Calcolo della pressione minima per un movimento stabile
Determinare la pressione minima necessaria per un movimento stabile:
- Calcolare la forza necessaria per superare il carico esterno.
- Aggiungere la forza di attrito (in genere 3-20% della forza massima)
- Dividere per l'area effettiva del pistone
- Aggiungere un fattore di stabilità (tipicamente 10-30%)
Ad esempio, in un cilindro senza stelo con alesaggio di 40 mm, con un carico di 10 kg e un attrito di 15%:
| Parametro | Calcolo | Risultato |
|---|---|---|
| Forza di carico | 10 kg × 9,81 m/s² | 98.1N |
| Forza di attrito | 15% di forza massima a 6 bar | ~45N |
| Forza totale | 98,1N + 45N | 143.1N |
| Area del pistone | π × (0,02m)² | 0.00126m² |
| Pressione minima | 143,1N ÷ 0,00126m² | 113.571 Pa (1,14 bar) |
| Con 20% Fattore di stabilità | 1,14 bar × 1,2 | 1,37 bar |
Applicazione reale: Risparmio energetico attraverso l'ottimizzazione della pressione
L'anno scorso ho lavorato con Robert, un ingegnere di produzione di un impianto di produzione di mobili nel Michigan. La sua linea di assemblaggio automatizzata utilizzava cilindri senza stelo che funzionavano con una pressione di alimentazione di 6 bar, indipendentemente dal carico.
Dopo aver analizzato la sua applicazione, abbiamo stabilito che la maggior parte dei movimenti richiedeva solo 2,5-3 bar per un funzionamento stabile. Installando regolatori di pressione proporzionaliAbbiamo ridotto il consumo d'aria di 40% mantenendo lo stesso tempo di ciclo. In questo modo abbiamo risparmiato circa $12.000 all'anno in termini di costi energetici, riducendo al contempo l'usura delle tenute e prolungando gli intervalli di manutenzione.
Relazione velocità-pressione nei sistemi reali
In pratica, la relazione tra pressione e velocità non è perfettamente lineare a causa di:
- Limitazioni di flusso: Il dimensionamento delle valvole e degli attacchi influisce sulla velocità massima raggiungibile
- Effetti di comprimibilità: L'aria è comprimibile e causa ritardi nell'accelerazione.
- Fenomeni di stick-slip: Le caratteristiche di attrito cambiano con la velocità
- Effetti inerziali: L'accelerazione della massa richiede una forza/pressione aggiuntiva
Come si calcola l'accelerazione massima possibile nei cilindri pneumatici?
La comprensione dei limiti di accelerazione è fondamentale per prevenire urti, vibrazioni e guasti prematuri nei sistemi pneumatici.
L'accelerazione massima possibile in un cilindro pneumatico si calcola con a = (P × A - F - Fr)/m, dove a è l'accelerazione, P è la pressione, A è l'area del pistone, F è il carico esterno, Fr è la resistenza all'attrito e m è la massa in movimento. Questa equazione definisce i limiti fisici della velocità con cui un attuatore pneumatico può avviare o arrestare il movimento.
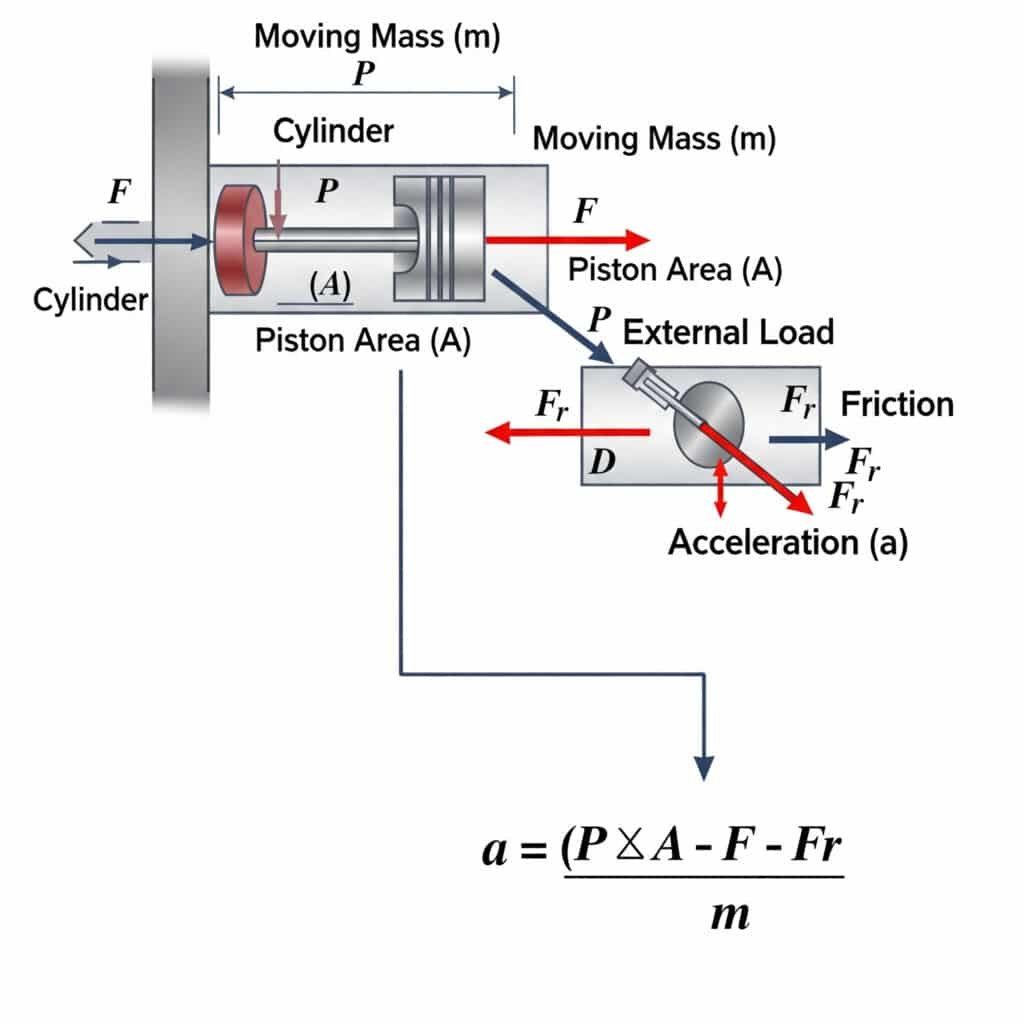
I limiti teorici di accelerazione hanno importanti implicazioni pratiche per la progettazione del sistema e la selezione dei componenti.
Derivazione dell'equazione del limite di accelerazione
L'equazione del limite di accelerazione deriva da La seconda legge di Newton2 (F = ma):
- La forza netta disponibile per l'accelerazione è: Fnet = Fpressione - Fcarico - Ffrizione
- Pressione F = P × A
- Pertanto: a = Fnet/m = (P × A - F - Fr)/m
Limiti pratici di accelerazione per diversi tipi di cilindro
I diversi design dei cilindri hanno limiti pratici di accelerazione diversi:
| Tipo di cilindro | Accelerazione massima tipica | Fattori limitanti |
|---|---|---|
| Cilindro a stelo standard | 10-15 m/s² | Instabilità dell'asta, carichi sui cuscinetti |
| Cilindro senza stelo (magnetico) | 8-12 m/s² | Forza di accoppiamento magnetico |
| Cilindro senza stelo (meccanico) | 15-25 m/s² | Design della guarnizione/cuscinetto, attrito interno |
| Cilindro guida | 20-30 m/s² | Rigidità del sistema di guida, capacità portante |
| Cilindro d'impatto | 50-100+ m/s² | Progettato appositamente per le accelerazioni elevate |
Considerazioni sulla massa nei calcoli dell'accelerazione
Quando si calcola l'accelerazione, è fondamentale includere tutte le masse in movimento:
- Gruppo pistone: Include pistone, guarnizioni ed elementi di collegamento.
- Massa di carico: Carico esterno in movimento
- Massa effettiva dell'aria in movimento: Spesso trascurabile ma rilevante nelle applicazioni ad alta velocità
- Massa aggiuntiva dovuta ai componenti di montaggio: Staffe, sensori, ecc.
Una volta ho aiutato un cliente in Francia che stava sperimentando misteriosi guasti nel suo sistema di cilindri senza stelo. Il cilindro era stato dimensionato correttamente per un carico di 15 kg, ma si guastava costantemente dopo poche migliaia di cicli.
Dopo aver indagato, abbiamo scoperto che non aveva tenuto conto della massa di 12 kg della piastra di montaggio e degli accessori. La massa effettiva in movimento era quasi il doppio di quella calcolata, causando forze di accelerazione che superavano i limiti di progetto del cilindro. Dopo il passaggio a un cilindro più grande, i guasti sono cessati completamente.
Metodi di controllo dell'accelerazione
Per controllare l'accelerazione entro limiti di sicurezza:
- Valvole di controllo del flusso: Limitare la portata durante il movimento iniziale
- Valvole proporzionali: Fornisce un aumento controllato della pressione
- Accelerazione multistadio: Utilizzare aumenti di pressione graduali
- Smorzamento meccanico: Aggiungere ammortizzatori esterni
- Controllo elettronico: Utilizzo sistemi servo-pneumatici3 con feedback di accelerazione
Perché il tempo di ammortizzazione è importante e come si calcola?
Un'adeguata ammortizzazione di fine corsa è essenziale per prevenire i danni da impatto, ridurre la rumorosità e prolungare la vita dei cilindri pneumatici. La comprensione del tempo di ammortizzazione aiuta gli ingegneri a progettare sistemi che bilanciano il tempo di ciclo con la longevità dei componenti.
Il tempo di ammortizzazione nei cilindri pneumatici si calcola con l'equazione t = √(2s/a), dove t è il tempo, s è la lunghezza della corsa di ammortizzazione e a è la decelerazione. Questo tempo rappresenta il tempo necessario per decelerare in modo sicuro la massa in movimento prima dell'impatto, che è fondamentale per evitare danni al cilindro e ai componenti collegati.

Esploriamo gli aspetti pratici del calcolo del tempo di ammortizzazione e le loro implicazioni per la progettazione del sistema.
La fisica alla base dei cuscini pneumatici
Ammortizzazione pneumatica funziona attraverso una compressione controllata dell'aria e uno scarico limitato:
- Quando il pistone entra nella camera del cuscino, il percorso di scarico viene ristretto.
- L'aria intrappolata si comprime, creando una crescente contropressione.
- Questa contropressione crea una forza contraria che decelera il pistone.
- Il profilo di decelerazione dipende dalla struttura e dalla regolazione del cuscino.
Calcolo del tempo di ammortizzazione ottimale
Il tempo di ammortizzazione ottimale bilancia la prevenzione degli impatti con l'efficienza del ciclo:
| Parametro | Formula | Esempio |
|---|---|---|
| Distanza di ammortizzazione | In base al design del cilindro | 15 mm (tipico per un foro di 40 mm) |
| Decelerazione richiesta | a = v²/(2s) | Per v=0,5m/s, s=15mm: a = 8,33m/s² |
| Tempo di ammortizzazione | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Aumento di pressione | P = P₀(V₀/V)^γ | Dipende dalla geometria della camera del cuscino |
Fattori che influenzano le prestazioni di ammortizzazione
Diversi fattori influenzano le prestazioni effettive dell'ammortizzazione:
- Design della guarnizione a cuscino: Influisce sulla perdita d'aria durante l'ammortizzazione
- Regolazione della valvola a spillo: Controlla il tasso di restrizione dei gas di scarico
- Massa in movimento: I carichi più pesanti richiedono un tempo di ammortizzazione più lungo
- Velocità di avvicinamento: Le velocità più elevate richiedono una maggiore distanza tra i cuscini
- Pressione di esercizio: Influenza la massima forza di contrasto disponibile
Tipi di ammortizzatori e loro applicazioni
Diversi meccanismi di ammortizzazione sono adatti a diverse applicazioni:
| Tipo di ammortizzazione | Caratteristiche | Le migliori applicazioni |
|---|---|---|
| Ammortizzazione fissa | Semplice, non regolabile | Carichi leggeri, funzionamento costante |
| Ammortizzazione regolabile | Regolabile con valvole a spillo | Carichi variabili, applicazioni flessibili |
| Ammortizzazione autoregolabile | Si adatta a condizioni diverse | Modifica delle velocità e dei carichi |
| Ammortizzatori esterni | Elevato assorbimento di energia | Carichi pesanti, velocità elevate |
| Ammortizzazione elettronica | Decelerazione controllata con precisione | Sistemi servo-pneumatici |
Caso di studio: Ottimizzazione dell'ammortizzazione nelle applicazioni a ciclo elevato
Di recente ho lavorato con Thomas, un ingegnere progettista di un produttore di componenti automobilistici in Germania. La sua linea di assemblaggio utilizzava cilindri senza stelo che operavano a 45 cicli al minuto, ma si verificavano frequenti guasti alle guarnizioni e danni alle staffe di montaggio.
L'analisi ha rivelato che il tempo di ammortizzazione era troppo breve per la massa in movimento, causando forze d'impatto di quasi 3G a ogni fine corsa. Aumentando la corsa di ammortizzazione da 12 mm a 20 mm e ottimizzando le impostazioni della valvola a spillo, abbiamo prolungato il tempo di ammortizzazione da 0,04 a 0,07 secondi.
Questa modifica apparentemente piccola ha ridotto le forze d'impatto di oltre 60%, ha eliminato completamente i danni alla staffa e ha prolungato la durata della tenuta da 3 mesi a oltre un anno, il tutto mantenendo il tempo di ciclo richiesto.
Procedura pratica di regolazione del cuscino
Per prestazioni di ammortizzazione ottimali nei cilindri senza stelo:
- Iniziare con le valvole del cuscino completamente aperte (restrizione minima)
- Chiudere gradualmente la valvola del cuscino fino a ottenere una decelerazione regolare.
- Test con carichi minimi e massimi previsti
- Verifica delle prestazioni di ammortizzazione nell'intera gamma di velocità
- Ascoltate i suoni d'impatto che indicano un'ammortizzazione insufficiente.
- Misurare il tempo di decelerazione effettivo per confermare i calcoli.
Conclusione
La comprensione dei principi della cinematica del pistone, dai requisiti di pressione per una velocità costante ai limiti di accelerazione e al calcolo del tempo di ammortizzazione, è essenziale per progettare sistemi pneumatici efficienti e affidabili. Applicando questi principi alle vostre applicazioni con cilindri senza stelo, potrete ottimizzare le prestazioni, ridurre il consumo energetico e prolungare significativamente la durata dei componenti.
Domande frequenti sulla cinematica dei pistoni nei sistemi pneumatici
Di quale pressione ho bisogno per una specifica velocità del cilindro?
La pressione necessaria dipende dal carico, dall'attrito e dall'area del cilindro. La si calcola con P = (F + Fr)/A, dove F è la forza del carico esterno, Fr è la resistenza all'attrito e A è l'area del pistone. Per un tipico cilindro senza stelo che muove un carico di 10 kg in orizzontale, sono necessari circa 1,5-2 bar per un movimento stabile a velocità moderate.
A che velocità può accelerare un cilindro pneumatico?
L'accelerazione massima di un cilindro pneumatico si calcola con a = (P × A - F - Fr)/m. I tipici cilindri senza stelo possono raggiungere un'accelerazione di 10-25 m/s² a seconda della progettazione. Ciò si traduce nel raggiungimento di una velocità di 0,5 m/s in circa 20-50 millisecondi in condizioni ottimali.
Quali fattori limitano la velocità massima di un cilindro senza stelo?
La velocità massima è limitata dalla capacità di flusso della valvola, dal volume di alimentazione dell'aria, dal dimensionamento dell'attacco, dalle capacità di ammortizzazione e dal design della tenuta. La maggior parte dei cilindri senza stelo standard sono progettati per velocità massime di 0,8-1,5 m/s, anche se i modelli specializzati ad alta velocità possono raggiungere i 2-3 m/s.
Come si calcola l'ammortizzazione corretta per la propria applicazione?
Calcolare l'ammortizzazione adeguata determinando l'energia cinetica (KE = ½mv²) del carico in movimento e assicurandosi che il sistema di ammortizzazione sia in grado di assorbire tale energia. Il tempo di ammortizzazione deve essere calcolato con t = √(2s/a), dove s è la distanza del cuscino e a è il tasso di decelerazione desiderato.
Cosa succede se il mio cilindro pneumatico accelera troppo rapidamente?
Un'accelerazione eccessiva può causare stress meccanico sui componenti di montaggio, usura prematura delle guarnizioni, aumento delle vibrazioni e della rumorosità, potenziale spostamento del carico o danni e riduzione della precisione del sistema. Può anche causare movimenti a scatti che influiscono sulla qualità del prodotto nelle applicazioni di precisione.
In che modo l'orientamento del carico influisce sulla pressione necessaria per il movimento?
L'orientamento del carico influisce in modo significativo sui requisiti di pressione. I carichi verticali che si muovono contro la gravità richiedono una pressione aggiuntiva per vincere la forza gravitazionale (P = F/A + Fg/A + Fr/A). I carichi orizzontali devono superare solo l'attrito e l'inerzia. I carichi inclinati si collocano tra questi estremi in base al seno dell'angolo.
-
Fornisce una spiegazione fondamentale della cinematica, la branca della meccanica che descrive il moto degli oggetti senza considerare le forze che causano il moto.
segnale di ingresso elettronico, consentendo un controllo pneumatico avanzato. ↩ -
Dettagli sulla Seconda Legge di Newton (F=ma), il principio fondamentale della fisica che mette in relazione la forza che agisce su un oggetto con la sua massa e la sua accelerazione e che è alla base di tutti i calcoli dinamici. ↩
-
Descrive la servo-pneumatica, una tecnologia di controllo avanzata che combina la potenza della pneumatica con la precisione del controllo elettronico ad anello chiuso per ottenere profili di posizionamento e movimento estremamente accurati. ↩


