Avete problemi di bassa velocità dei cilindri, di movimento incoerente o di forza insufficiente nei vostri sistemi pneumatici? Questi problemi comuni spesso derivano da una causa incompresa: la resistenza al flusso. Molti ingegneri dimensionano i loro componenti pneumatici solo in base ai requisiti di pressione e forza, trascurando l'impatto critico della resistenza al flusso sulle prestazioni reali.
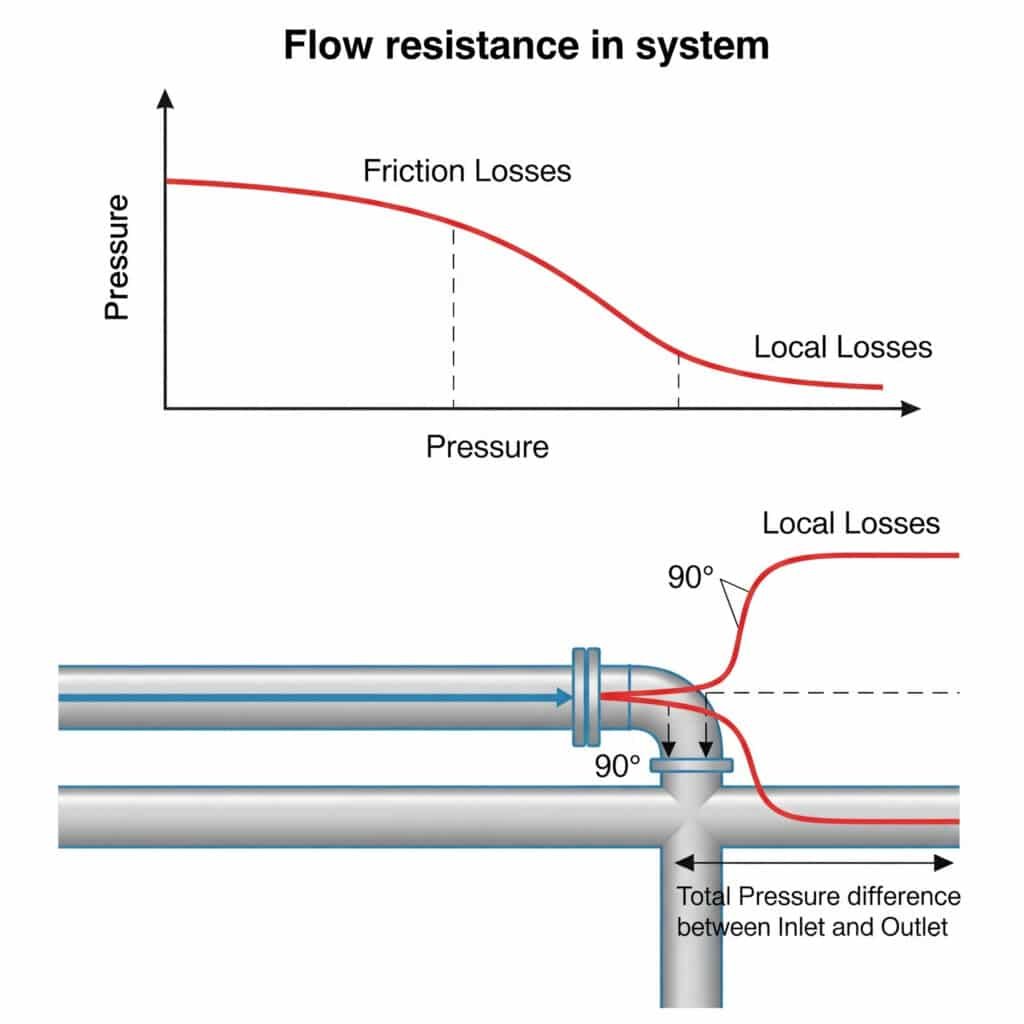
La resistenza al flusso nei sistemi pneumatici crea perdite di carico che riducono la forza disponibile, limitano la velocità massima e causano un movimento incoerente. Questa resistenza deriva sia dall'attrito lungo i tubi rettilinei (perdite per attrito) sia dalle interruzioni in corrispondenza di raccordi, curve e valvole (perdite locali). Insieme, queste resistenze possono ridurre le prestazioni effettive del sistema di 20-50% rispetto ai calcoli teorici.
Negli oltre 15 anni trascorsi in Bepto a lavorare con i sistemi pneumatici, ho visto innumerevoli casi in cui la comprensione e la gestione della resistenza al flusso hanno trasformato sistemi poco efficienti in operazioni affidabili ed efficienti. Permettetemi di condividere ciò che ho imparato sul calcolo e la minimizzazione di questi killer nascosti delle prestazioni.
Indice dei contenuti
- Come si calcolano effettivamente le perdite per attrito nelle linee pneumatiche?
- Perché il metodo della lunghezza equivalente è fondamentale per una progettazione accurata del sistema?
- Cosa succede quando l'aria fluisce attraverso sezioni ad alesaggio ridotto?
- Conclusione
- Domande frequenti sulla resistenza al flusso nei sistemi pneumatici
Come si calcolano effettivamente le perdite per attrito nelle linee pneumatiche?
Le perdite per attrito nei tubi rettilinei sono alla base dei calcoli della resistenza al flusso, ma molti ingegneri si affidano a regole empiriche troppo semplici che portano a sistemi sottodimensionati.
Le perdite per attrito nelle linee pneumatiche sono calcolate con la formula Equazione di Darcy-Weisbach1ΔP = λ(L/D)(ρv²/2), dove λ è il fattore di attrito, L è la lunghezza del tubo, D il diametro del tubo, ρ la densità dell'aria e v la velocità del flusso. Per i sistemi pneumatici, il fattore di attrito λ varia in base a Numero di Reynolds2 e la rugosità relativa, ed è tipicamente determinata utilizzando tabelle di ricerca o il metodo della Diagramma di Moody3.
La comprensione delle perdite per attrito ha implicazioni pratiche per la progettazione e la risoluzione dei problemi del sistema. Permettetemi di suddividere il tutto in informazioni utili per l'azione.
Utilizzo efficace delle tabelle dei fattori di attrito
Il fattore di attrito (λ) è il parametro chiave per il calcolo delle perdite di carico, ma la determinazione del suo valore richiede la considerazione delle condizioni di flusso:
| Regime di flusso | Numero di Reynolds (Re) | Determinazione del fattore di attrito |
|---|---|---|
| Flusso laminare | Re < 2000 | λ = 64/Re |
| Flusso transitorio | 2000 < Re < 4000 | Inaffidabile: evitare di progettare in questa fascia di valori |
| Flusso turbolento | Re > 4000 | Utilizzare tabelle di ricerca basate sulla rugosità relativa (ε/D) |
Tabella di ricerca del fattore di attrito pratico
Per il flusso turbolento nei sistemi pneumatici, utilizzare questa tabella semplificata:
| Materiale del tubo | Rugosità relativa (ε/D) | Fattore di attrito (λ) ai comuni numeri di Reynolds |
|---|---|---|
| Re = 10.000 | ||
| Tubi lisci (PVC, poliuretano) | 0.0001 – 0.0005 | 0.031 |
| Tubi di alluminio | 0.001 – 0.002 | 0.035 |
| Acciaio zincato | 0.003 – 0.005 | 0.042 |
| Acciaio arrugginito | 0.01 – 0.05 | 0.054 |
Calcolo delle perdite di carico nei sistemi pneumatici reali
Vediamo un esempio pratico:
| Parametro | Valore/Calcolo | Esempio |
|---|---|---|
| Diametro del tubo (D) | Diametro interno | 8 mm (0,008 m) |
| Lunghezza del tubo (L) | Lunghezza totale del rettilineo | 5m |
| Portata (Q) | Dai requisiti di sistema | 20 litri standard/secondo |
| Densità dell'aria (ρ) | Alla pressione di esercizio | 7,2 kg/m³ a 6 bar |
| Velocità del flusso (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Numero di Reynolds (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Rugosità relativa | Per tubi in poliuretano | 0.0003 |
| Fattore di attrito (λ) | Dalla tabella di ricerca | 0.017 |
| Perdita di carico (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Applicazione reale: Risolvere i problemi di velocità dei cilindri
L'anno scorso ho lavorato con Sarah, un ingegnere di produzione di un'azienda di attrezzature per l'imballaggio del Wisconsin. Il suo sistema con cilindro senza stelo funzionava solo a 60% della velocità prevista, nonostante avesse un cilindro di dimensioni corrette e una pressione di alimentazione adeguata.
Dopo aver analizzato il suo sistema, ho scoperto che utilizzava tubi da 6 mm per un'applicazione ad alto flusso. Le perdite per attrito causavano una caduta di pressione di 2,1 bar, riducendo significativamente la forza e la velocità disponibili. Passando a tubi da 10 mm, abbiamo ridotto la caduta di pressione a 0,4 bar e il sistema ha raggiunto immediatamente le prestazioni richieste senza altre modifiche.
Fattori che influenzano le perdite per attrito nei sistemi reali
Diversi fattori influenzano le perdite per attrito effettive:
- Temperatura dell'aria: Le temperature più elevate aumentano la viscosità e l'attrito.
- Contaminazione: Sporco e olio possono aumentare la rugosità effettiva
- Curvatura dei tubi: La micro-deformazione dei tubi piegati aumenta la resistenza
- Deterioramento per età: Corrosione e depositi aumentano la rugosità nel tempo
- Pressione di esercizio: Pressioni più elevate aumentano la densità e le perdite
Perché il metodo della lunghezza equivalente è fondamentale per una progettazione accurata del sistema?
Le perdite locali in corrispondenza di raccordi, valvole e curve sono spesso superiori alle perdite per attrito nei tubi rettilinei, ma molti ingegneri le ignorano o utilizzano metodi di stima approssimativi che causano problemi di prestazioni.
Il metodo della lunghezza equivalente converte le perdite locali di raccordi e valvole in una lunghezza equivalente di tubo rettilineo che causerebbe la stessa perdita di pressione. Si calcola con Le = K(D/λ), dove Le è la lunghezza equivalente, K è la perdita di carico. coefficiente di perdita locale4D è il diametro del tubo e λ è il fattore di attrito. Questo metodo semplifica i calcoli e fornisce previsioni più accurate sulle prestazioni del sistema.
Vediamo come applicare efficacemente questo metodo nella progettazione di sistemi pneumatici.
Tabelle delle lunghezze equivalenti per i componenti pneumatici più comuni
Ecco una pratica tabella di riferimento per i comuni componenti pneumatici:
| Componente | Valore K | Lunghezza equivalente (Le/D) |
|---|---|---|
| Gomito a 90° (affilato) | 0.9 | 30 |
| Gomito a 90° (raggio standard) | 0.3 | 10 |
| Gomito a 45° | 0.2 | 7 |
| Giunzione a T (flusso passante) | 0.3 | 10 |
| Giunzione a T (flusso di diramazione) | 1.0 | 33 |
| Valvola a sfera (completamente aperta) | 0.1 | 3 |
| Valvola a saracinesca (completamente aperta) | 0.2 | 7 |
| Attacco rapido | 0.4-0.8 | 13-27 |
| Valvola di ritegno | 1.5-2.5 | 50-83 |
| Valvola di controllo del flusso standard | 1.0-3.0 | 33-100 |
Applicazione del metodo della lunghezza equivalente
Per utilizzare questo metodo in modo efficace:
- Identificare tutti i componenti del circuito pneumatico
- Trovare il valore K o il rapporto di lunghezza equivalente (Le/D) per ogni componente.
- Calcolare la lunghezza equivalente moltiplicando per il diametro del tubo.
- Aggiungere tutte le lunghezze equivalenti alla lunghezza effettiva del tubo diritto
- Utilizzare la lunghezza effettiva totale nei calcoli della perdita per attrito.
Ad esempio, un sistema con 5 m di tubo diritto da 8 mm più quattro gomiti a 90°, un raccordo a T e due raccordi rapidi:
| Componente | Quantità | Le/D | Lunghezza equivalente |
|---|---|---|---|
| Gomiti a 90° | 4 | 10 | 4 × 10 × 0,008 m = 0,32 m |
| Giunzione a T | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Collegamenti rapidi | 2 | 20 | 2 × 20 × 0,008 m = 0,32 m |
| Lunghezza totale equivalente | 0.72m | ||
| Lunghezza effettiva del rettilineo | 5.00m | ||
| Lunghezza totale effettiva | 5.72m |
Ciò significa che il vostro sistema da 5 m si comporta in realtà come un sistema da 5,72 m a causa delle perdite locali: un aumento di 14,4% della lunghezza effettiva.
Caso di studio: Ottimizzazione del posizionamento delle valvole nei sistemi di assemblaggio
Di recente ho aiutato Miguel, un ingegnere dell'automazione di uno stabilimento di assemblaggio di componenti elettronici in Arizona. Il suo sistema pick-and-place presentava variazioni incoerenti del movimento e del tempo di ciclo, nonostante utilizzasse componenti di alta qualità.
L'analisi ha rivelato che il collettore delle valvole si trovava a 3 m di distanza dai cilindri e che il circuito comprendeva numerosi raccordi. Il calcolo della lunghezza equivalente ha mostrato che la distanza effettiva di 3 m aveva una lunghezza effettiva di 7,2 m a causa delle perdite locali, più del doppio della distanza del tubo diritto!
Avvicinando il collettore delle valvole ai cilindri ed eliminando alcuni raccordi, abbiamo ridotto la lunghezza effettiva da 7,2 m a 2,1 m. In questo modo abbiamo ridotto la caduta di pressione di 70%, ottenendo un movimento costante e una riduzione del tempo di ciclo di 15%.
Consigli pratici per ridurre al minimo le perdite locali
Per ridurre le perdite locali nei sistemi pneumatici:
- Usare gomiti arrotondati o spazzati invece di curve strette (riduce il valore K di 67%)
- Ridurre al minimo il numero di raccordi pianificando percorsi più diretti
- Selezionare componenti a basso coefficiente di attrito come le valvole a sfera a passaggio totale, ove opportuno
- Dimensionare correttamente i raccordi - i raccordi sottodimensionati causano perdite sproporzionate
- Posizionare le valvole vicino agli attuatori per ridurre al minimo la lunghezza effettiva del tubo
Cosa succede quando l'aria fluisce attraverso sezioni ad alesaggio ridotto?
Sezioni di foro ridotte nei circuiti pneumatici, come valvole parzialmente chiuse, raccordi sottodimensionati o transizioni di diametro, creano restrizioni di flusso significative che possono influire pesantemente sulle prestazioni del sistema.
Quando l'aria passa attraverso sezioni a foro ridotto, perdite di carico5 si verificano secondo la formula ΔP = ρ(v₂² - v₁²)/2, dove v₁ è la velocità prima della restrizione e v₂ è la velocità nella restrizione. Questo può essere compensato utilizzando il fattore di compensazione del rapporto di alesaggio C = (1 - (d/D)⁴), dove d è il diametro ridotto e D è il diametro originale. Questo fattore aiuta a prevedere le prestazioni effettive del sistema e a evitare il sottodimensionamento dei componenti.
Esaminiamo le implicazioni pratiche delle sezioni di alesaggio ridotte e come tenerne conto nella progettazione del sistema.
Calcolo delle gocce di pressione alle transizioni di diametro
Quando l'aria passa da un diametro più grande a uno più piccolo, la perdita di carico può essere calcolata con il seguente metodo:
| Parametro | Formula | Esempio |
|---|---|---|
| Diametro originale (D) | Da specifiche | 10 mm |
| Diametro ridotto (d) | Da specifiche | 6 mm |
| Rapporto di alesaggio (d/D) | Divisione semplice | 0.6 |
| Portata (Q) | Dai requisiti di sistema | 15 litri standard/secondo |
| Velocità nel tubo originale (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Velocità nella sezione ridotta (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Perdita di carico (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Fattore di compensazione (C) | C = (1 - (d/D)⁴) | 0.87 |
Scenari comuni di riduzione dell'alesaggio e loro impatto
Ecco come le diverse riduzioni del foro influiscono sulla capacità di flusso:
| Riduzione dell'alesaggio | Riduzione della capacità di flusso | Aumento della caduta di pressione |
|---|---|---|
| Da 10 mm a 8 mm | 36% | 2.4× |
| Da 10 mm a 6 mm | 64% | 7.7× |
| Da 10 mm a 4 mm | 84% | 39× |
| Da 8 mm a 6 mm | 44% | 3.2× |
| Da 8 mm a 4 mm | 75% | 16× |
| Da 6 mm a 4 mm | 56% | 5.1× |
Questi numeri evidenziano perché riduzioni apparentemente minime del diametro possono avere effetti drammatici sulle prestazioni del sistema.
L'effetto cumulativo di più restrizioni
Nei circuiti pneumatici reali, si verificano più restrizioni in serie. Il loro effetto è cumulativo e può essere calcolato utilizzando:
- Convertire ogni restrizione nel suo fattore C equivalente
- Calcolare il fattore C totale: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Utilizzare questo fattore totale per determinare la riduzione complessiva delle prestazioni del sistema.
Caso di studio: Risoluzione dei problemi di disallineamento valvola-attuatore
Il mese scorso ho lavorato con Thomas, un supervisore della manutenzione di uno stabilimento di produzione di mobili nella Carolina del Nord. Il suo nuovo sistema di cilindri senza stelo funzionava a meno della metà della velocità prevista, nonostante l'utilizzo della dimensione della valvola raccomandata dal produttore.
L'indagine ha rivelato la presenza di riduzioni multiple dei fori nel suo circuito:
- Linea di alimentazione da 10 mm a porte della valvola da 8 mm (C₁ = 0,36)
- Porte valvola da 8 mm a raccordi da 6 mm (C₂ = 0,44)
- Raccordi da 6 mm a porte cilindro da 8 mm con restrizioni interne (C₃ = 0,32)
Il fattore di compensazione totale era Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, il che significa che il sistema perdeva 75% della sua capacità di flusso teorica!
Con l'aggiornamento a componenti correttamente dimensionati in tutto il sistema, abbiamo eliminato queste limitazioni e ottenuto le prestazioni richieste senza modificare il cilindro o la pressione di alimentazione.
Strategie pratiche per ridurre al minimo le perdite di riduzione dell'alveolo
Per ridurre le perdite dovute alla riduzione dei fori:
- Dimensionare i componenti in modo coerente in tutto il circuito pneumatico
- Utilizzare il tubo di dimensioni più grandi possibili per applicazioni ad alto flusso
- Prestare attenzione alle limitazioni dei componenti interni, non solo le dimensioni delle connessioni
- Considerare percorsi di flusso paralleli per esigenze di alta portata
- Eliminazione di adattatori e transizioni non necessari dove possibile
Il principio dell'"anello più debole" nei sistemi pneumatici
Ricordate che le prestazioni del sistema pneumatico sono limitate dal componente più restrittivo. Un singolo elemento sottodimensionato può annullare i vantaggi di componenti correttamente dimensionati in altri punti del sistema.
Ad esempio, un sistema con tubi da 10 mm, valvole da 10 mm, ma raccordi da 6 mm al cilindro avrà essenzialmente le stesse prestazioni di un sistema con componenti da 6 mm in tutto il suo complesso, a un costo superiore.
Conclusione
La comprensione e il calcolo corretto della resistenza al flusso, attraverso le tabelle dei fattori di attrito, i metodi di lunghezza equivalente e la compensazione dell'alesaggio ridotto, sono essenziali per progettare sistemi pneumatici che funzionino come previsto in condizioni reali. Applicando questi metodi di calcolo e principi di progettazione, è possibile ottimizzare le applicazioni dei cilindri senza stelo e altri sistemi pneumatici per ottenere le massime prestazioni e affidabilità.
Domande frequenti sulla resistenza al flusso nei sistemi pneumatici
Qual è la caduta di pressione accettabile in un sistema pneumatico?
La caduta di pressione accettabile dipende dai requisiti dell'applicazione, ma come linea guida generale, limitare la caduta di pressione totale a 10-15% della pressione di alimentazione per un funzionamento efficiente. Per un sistema a 6 bar, ciò significa mantenere la perdita di carico totale sotto 0,6-0,9 bar. Le applicazioni critiche possono richiedere perdite di carico ancora più basse, da 5 a 8%, per mantenere prestazioni costanti.
Qual è la relazione tra il diametro del tubo e la caduta di pressione?
La caduta di pressione è inversamente proporzionale alla quinta potenza del diametro (D⁵) per il flusso turbolento nei sistemi pneumatici. Ciò significa che il raddoppio del diametro del tubo riduce la caduta di pressione di circa 32 volte. Ad esempio, passando da un tubo di 6 mm a uno di 12 mm si può ridurre la perdita di carico da 1,5 bar a soli 0,047 bar nelle stesse condizioni di flusso.
Come si determina la giusta dimensione del tubo per la propria applicazione pneumatica?
Selezionare le dimensioni del tubo in base ai requisiti di portata e alla caduta di pressione accettabile. Calcolare il numero di Reynolds e il fattore di attrito, quindi utilizzare l'equazione di Darcy-Weisbach per determinare la perdita di carico per diversi diametri. Scegliere il diametro più piccolo che mantiene la caduta di pressione entro limiti accettabili (in genere <10% della pressione di alimentazione), tenendo conto dei vincoli di spazio e dei costi.
Cosa crea maggiori restrizioni: un gomito a 90° o 5 metri di tubo diritto?
Un gomito a 90° crea una resistenza equivalente a 30 diametri di tubo diritto. Per i tubi da 8 mm, un gomito acuto equivale a circa 240 mm (30 × 8 mm) di tubo diritto. Ciò significa che 5 metri di tubo diritto creano una restrizione circa 21 volte maggiore rispetto a un singolo gomito. Tuttavia, i sistemi spesso contengono più gomiti e raccordi, il cui effetto cumulativo può superare le perdite di lunghezza rettilinea.
In che modo i raccordi a innesto rapido influiscono sulle prestazioni del sistema?
I raccordi a innesto rapido standard introducono in genere una perdita locale equivalente a 15-25 diametri di tubo diritto. Inoltre, molti raccordi rapidi hanno restrizioni interne inferiori alla loro dimensione nominale. Un attacco rapido da "10 mm" potrebbe avere una restrizione interna di soli 7-8 mm, creando una riduzione del foro che può ridurre la capacità di flusso di 50-70% in quel punto.
Qual è l'impatto delle valvole di controllo del flusso parzialmente chiuse sulle prestazioni del sistema?
Una valvola di controllo del flusso chiusa a 50% dell'area del suo foro completo non riduce il flusso di soli 50%, ma di circa 75% a causa della relazione non lineare tra diametro e capacità di flusso. La perdita di carico aumenta in base al quadrato della variazione di velocità, quindi il dimezzamento del diametro effettivo aumenta la perdita di carico di circa 16 volte nelle stesse condizioni di flusso.
-
Fornisce una descrizione dettagliata dell'equazione di Darcy-Weisbach, una formula fondamentale e ampiamente utilizzata nella fluidodinamica per calcolare le perdite di pressione dovute all'attrito in un tubo. ↩
-
Offre una chiara definizione del numero di Reynolds, una grandezza adimensionale critica utilizzata per prevedere i modelli di flusso (laminare o turbolento) in diverse situazioni di flusso fluido. ↩
-
Presenta il diagramma di Moody, un grafico completo che mette in relazione il fattore di attrito Darcy con il numero di Reynolds e la rugosità relativa, che è lo strumento standard per gli ingegneri per determinare le perdite di carico nelle tubazioni. ↩
-
Spiega il concetto di valore K, o coefficiente di perdita locale, un numero adimensionale utilizzato per caratterizzare la perdita di pressione in un raccordo o in una valvola nell'ambito del metodo della lunghezza equivalente. ↩
-
Illustra la fisica della caduta di pressione che si verifica quando un fluido passa attraverso una restrizione (un orifizio), basandosi sui principi dell'equazione di continuità e del principio di Bernoulli. ↩




