Qual è il volume di una sfera piatta nelle applicazioni dei cilindri pneumatici?

Serie OSP-P L'originale cilindro modulare senza stelo — Cilindro meccanico senza stelo OSP

Gli ingegneri si trovano in difficoltà nel calcolare i volumi dei componenti sferici appiattiti nei sistemi di cilindri pneumatici senza stelo. Calcoli di volume errati portano a errori di calcolo della pressione e a guasti del sistema.

Una sfera piatta (sferoide oblato) ha volume V = (4/3)πa²b, dove 'a' è il raggio equatoriale e 'b' è il raggio polare, comunemente trovato in accumulatore pneumatico¹ e le applicazioni di ammortizzazione.

Il mese scorso ho aiutato Andreas, un ingegnere progettista tedesco, il cui sistema di ammortizzazione pneumatica è fallito perché ha utilizzato il volume di una sfera standard anziché quello di uno sferoide oblato per le sue camere di accumulo appiattite.

Indice dei contenuti

Che cos'è una sfera piatta nelle applicazioni pneumatiche?
Come si calcola il volume di una sfera piatta?
Dove si usano le sfere piatte nei cilindri senza stelo?
In che modo l'appiattimento influisce sul volume e sulle prestazioni?

Che cos'è una sfera piatta nelle applicazioni pneumatiche?

Una sfera piatta, tecnicamente chiamata sferoide oblato²è una forma tridimensionale creata quando una sfera viene compressa lungo un asse, comunemente utilizzata nei progetti di accumulatori e ammortizzatori pneumatici.

Una sfera piatta risulta dall'appiattimento di una sfera perfetta lungo il suo asse verticale, creando una sezione trasversale ellittica con misure di raggio orizzontali e verticali diverse.

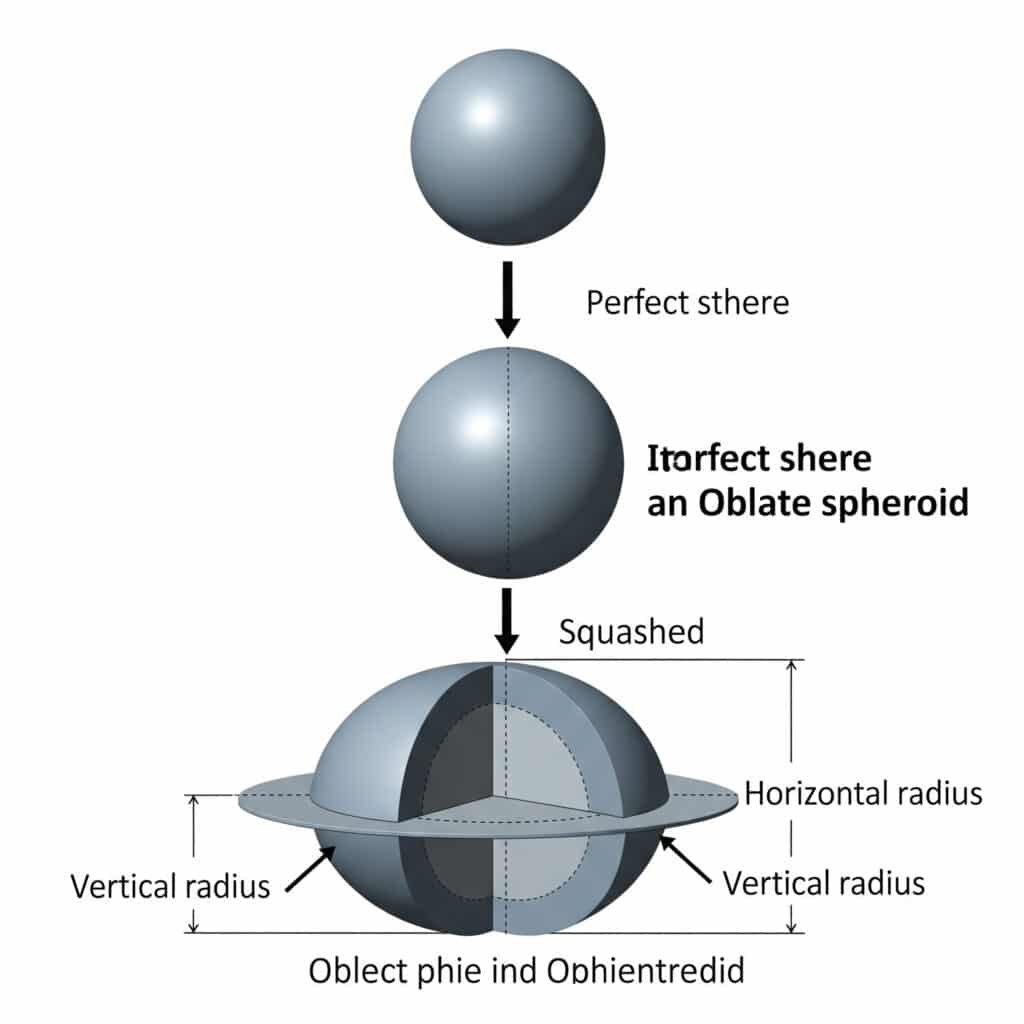
Diagramma in tre fasi che illustra la trasformazione di una sfera perfetta in una sfera piatta (sferoide oblato). Il processo mostra che la sfera viene schiacciata, ottenendo una forma con una sezione trasversale evidenziata e raggi verticali e orizzontali di diversa lunghezza chiaramente etichettati. — Diagramma della sfera piatta che mostra la forma di sferoide oblato

Definizione geometrica

Caratteristiche della forma

Sferoide oblato: Termine tecnico geometrico
Sfera appiattita: Descrizione industriale comune
Profilo ellittico: Vista trasversale
Simmetria rotazionale: Intorno all'asse verticale

Dimensioni chiave

Raggio equatoriale (a): Raggio orizzontale (maggiore)
Raggio polare (b): Raggio verticale (più piccolo)
Rapporto di appiattimento: b/a < 1,0
Rapporto d'aspetto: Rapporto tra altezza e larghezza

Sfera piatta vs. Sfera perfetta

Caratteristica	Sfera perfetta	Sfera piatta
Forma	Raggio uniforme	Compresso verticalmente
Formula del volume	(4/3)πr³	(4/3)πa²b
Sezione trasversale	Cerchio	Ellisse
Simmetria	Tutte le direzioni	Solo orizzontale

Rapporti di appiattimento comuni

Appiattimento della luce

Rapportob/a = 0,8-0,9
Applicazioni: Leggeri vincoli di spazio
Impatto sul volume: riduzione 10-20%
Prestazioni: Effetto minimo

Appiattimento moderato

Rapportob/a = 0,6-0,8
Applicazioni: Modelli di accumulatori standard
Impatto sul volume: riduzione 20-40%
Prestazioni: Variazioni di pressione evidenti

Appiattimento pesante

Rapportob/a = 0,3-0,6
Applicazioni: Gravi limitazioni di spazio
Impatto sul volume: riduzione 40-70%
Prestazioni: Considerazioni significative sulla progettazione

Applicazioni pneumatiche

Camere di accumulo

Incontro sfere piatte in:

Installazioni con limiti di spazio: Limiti di altezza
Progetti integrati: Costruito nei telai delle macchine
Applicazioni personalizzate: Requisiti specifici di volume
Progetti di retrofit: Adattare gli spazi esistenti

Sistemi di ammortizzazione

Smorzamento di fine corsa: Applicazioni dei cilindri senza stelo
Assorbimento degli urti: Gestione del carico di impatto
Regolazione della pressione: Controllo del funzionamento regolare
Riduzione del rumore: Funzionamento del sistema più silenzioso

Considerazioni sulla produzione

Metodi di produzione

Disegno profondo: Formatura della lamiera
Idroformatura: Processo di sagomatura di precisione
Lavorazione meccanica: Componenti unici personalizzati
Colata: Produzione in grandi volumi

Selezione del materiale

Acciaio: Applicazioni ad alta pressione
Alluminio: Progetti sensibili al peso
Acciaio inox: Ambienti corrosivi
Materiali compositi: Requisiti specifici

Come si calcola il volume di una sfera piatta?

Il calcolo del volume della sfera piatta richiede la formula dello sferoide oblato utilizzando le misure dei raggi equatoriali e polari per una progettazione accurata del sistema pneumatico.

Utilizzare la formula V = (4/3)πa²b dove "a" è il raggio equatoriale (orizzontale) e "b" è il raggio polare (verticale) per calcolare con precisione il volume della sfera piatta.

Ripartizione della formula del volume

Formula standard

V = (4/3)πa²b

V: Volume in unità cubiche
π: 3,14159 (costante matematica)
a: Raggio equatoriale (orizzontale)
b: Raggio polare (verticale)
4/3: Coefficiente di volume dello sferoide

Componenti della formula

Area equatoriale: πa² (sezione trasversale orizzontale)
Scala polareFattore b (compressione verticale)
Coefficiente di volume: 4/3 (costante geometrica)
Unità di risultato: Corrisponde alle unità del raggio di ingresso al cubo

Calcolo passo-passo

Processo di misurazione

Misurare il diametro equatoriale: Dimensione orizzontale più ampia
Calcolo del raggio equatoriale: a = diametro ÷ 2
Misurare il diametro polare: Dimensione verticale in altezza
Calcolo del raggio polare: b = altezza ÷ 2
Applicare la formula: V = (4/3)πa²b

Esempio di calcolo

Per un accumulatore pneumatico:

Diametro equatoriale: 100 mm → a = 50 mm
Diametro polare: 60 mm → b = 30 mm
Volume: V = (4/3)π(50)²(30)
Risultato: V = (4/3)π(2500)(30) = 314,159 mm³

Esempi di calcolo del volume

Raggio equatoriale	Raggio polare	Rapporto di appiattimento	Volume	Confronto con Sfera
50 mm	50 mm	1.0	523.599 mm³	100% (sfera perfetta)
50 mm	40 mm	0.8	418.879 mm³	80%
50 mm	30 mm	0.6	314.159 mm³	60%
50 mm	20 mm	0.4	209.440 mm³	40%

Strumenti di calcolo

Calcolo manuale

Calcolatrice scientifica: Con funzione π
Verifica della formula: Doppio controllo degli ingressi
Coerenza dell'unità: Mantenere le stesse unità per tutto il tempo
Precisione: Calcolo con cifre decimali appropriate

Strumenti digitali

Software di ingegneria: Calcoli del volume CAD
Calcolatori online: Strumenti sferoidi oblati
Formule del foglio di calcolo: Calcoli automatizzati
Applicazioni mobili: Strumenti di calcolo sul campo

Errori di calcolo comuni

Errori di misurazione

Raggio vs diametro: Utilizzo di una dimensione errata
Confusione dell'asse: Miscelazione di misure orizzontali e verticali
Incoerenza dell'unità: miscelazione in mm o in pollici
Perdita di precisione: Arrotondamento troppo anticipato

Errori di formula

Formula sbagliata: Utilizzo della sfera al posto dello sferoide
Inversione dei parametri: Scambio dei valori a e b
Errori di coefficiente: Fattore 4/3 mancante
approssimazione π: Usare 3.14 invece di 3.14159

Metodi di verifica

Tecniche di controllo incrociato

Software CAD: Calcolo del volume del modello 3D
Spostamento dell'acqua: Misura fisica del volume
Calcoli multipli: Confronto tra diversi metodi
Specifiche del produttore: Dati di volume pubblicati

Controlli di ragionevolezza

Riduzione del volume: Dovrebbe essere una sfera meno che perfetta
Appiattimento della correlazione: Più appiattimento = meno volume
Verifica dell'unità: I risultati corrispondono alla grandezza prevista
Idoneità all'applicazione: Il volume soddisfa i requisiti di sistema

Quando ho aiutato Maria, una progettista di sistemi pneumatici spagnola, a calcolare i volumi degli accumulatori per la sua installazione di cilindri senza stelo, abbiamo scoperto che i suoi calcoli originali utilizzavano formule a sfera anziché a sferoide oblato, con conseguente sovrastima del volume di 35% e prestazioni inadeguate del sistema.

Dove si usano le sfere piatte nei cilindri senza stelo?

Le sfere piatte vengono utilizzate in vari componenti di cilindri pneumatici senza stelo, dove i vincoli di spazio richiedono un'ottimizzazione del volume, pur mantenendo la funzionalità del recipiente in pressione.

Le sfere piatte sono comunemente utilizzate nelle camere di accumulo, nei sistemi di ammortizzazione e nei recipienti di pressione integrati nei gruppi di cilindri senza stelo, dove le limitazioni di altezza limitano i design sferici standard.

Applicazioni dell'accumulatore

Accumulatori integrati

Ottimizzazione dello spazio: Si adattano ai telai dei macchinari
Efficienza del volume: Massimo stoccaggio in un'altezza limitata
Stabilità della pressione: Funzionamento regolare durante i picchi di domanda
Integrazione del sistema: Integrato nelle basi di montaggio dei cilindri

Installazioni retrofit

Macchinari esistenti: Limiti di altezza
Progetti di aggiornamento: Aggiunta di accumulo ai sistemi più vecchi
Vincoli di spazio: Lavorare all'interno del progetto originale
Miglioramento delle prestazioni: Risposta del sistema migliorata

Sistemi di ammortizzazione

Smorzamento di fine corsa

Installo un'ammortizzazione a sfera piatta per:

Cilindri magnetici senza stelo: Decelerazione dolce
Cilindri senza stelo guidati: Riduzione dell'impatto
Cilindri senza stelo a doppio effetto: Ammortizzazione bidirezionale
Applicazioni ad alta velocità: Assorbimento degli urti

Regolazione della pressione

Lisciatura del flusso: Eliminare i picchi di pressione
Riduzione del rumore: Funzionamento più silenzioso
Protezione dei componenti: Riduzione dell'usura e delle sollecitazioni
Stabilità del sistema: Prestazioni costanti

Componenti specializzati

Serbatoi a pressione

Applicazioni personalizzate: Requisiti di spazio unici
Design multifunzione: Conservazione e montaggio combinati
Sistemi modulari: Configurazioni impilabili
Accesso per la manutenzione: Disegni utilizzabili

Camere per sensori

Monitoraggio della pressione: Sistemi di misura integrati
Rilevamento del flusso: Applicazioni di rilevamento della velocità
Diagnostica del sistema: Monitoraggio delle prestazioni
Sistemi di sicurezza: Integrazione dello scarico di pressione

Considerazioni sulla progettazione

Vincoli di spazio

Applicazione	Limite di altezza	Appiattimento tipico	Impatto del volume
Montaggio sotto il pavimento	50 mm	b/a = 0,3	Riduzione 70%
Integrazione delle macchine	100 mm	b/a = 0,6	Riduzione 40%
Applicazioni retrofit	150 mm	b/a = 0,8	Riduzione 20%
Montaggio standard	200 mm+	b/a = 0,9	Riduzione 10%

Requisiti di prestazione

Pressione nominale: Mantenere l'integrità strutturale
Capacità di volume: Soddisfare la domanda del sistema
Caratteristiche del flusso: Dimensionamento adeguato di ingresso/uscita
Accesso per la manutenzione: Considerazioni sulla manutenibilità

Esempi di installazione

Macchinari per l'imballaggio

Applicazione: Apparecchiature di riempimento ad alta velocità
Vincolo: Spazio in altezza di 40 mm
Soluzione: Accumulatore fortemente appiattito (b/a = 0,25)
Risultato75% riduzione del volume, prestazioni adeguate

Assemblaggio automobilistico

Applicazione: Sistema di posizionamento robotizzato
Vincolo: Integrazione nella base robotica
Soluzione: Appiattimento moderato (b/a = 0,7)
Risultato: 30% risparmio di spazio, mantenimento delle prestazioni

Lavorazione degli alimenti

Applicazione: Sistema di cilindri sanitari senza stelo
Vincolo: Autorizzazione per l'ambiente di lavaggio
Soluzione: Design personalizzato della sfera piatta
Risultato: Grado di protezione IP69K³ con volume ottimizzato

Specifiche di produzione

Dimensioni standard

Piccolo: 50 mm equatoriale, varie dimensioni polari
Medio: 100 mm equatoriali, variazioni di altezza
Grandeequatoriale da 200 mm, polarizzazione personalizzata
Personalizzato: Dimensioni specifiche per l'applicazione

Opzioni di materiale

Acciaio al carbonio: Applicazioni a pressione standard
Acciaio inox: Ambienti corrosivi
Alluminio: Installazioni sensibili al peso
Composito: Requisiti specifici

L'anno scorso ho lavorato con Thomas, un costruttore di macchine svizzero, che aveva bisogno di accumuli per la sua linea di confezionamento compatta. Gli accumulatori sferici standard non si adattavano ai limiti di altezza di 60 mm, quindi abbiamo progettato accumulatori a sfera piatta con rapporto b/a = 0,4, ottenendo 60% del volume originale e rispettando tutti i vincoli di spazio.

In che modo l'appiattimento influisce sul volume e sulle prestazioni?

L'appiattimento riduce significativamente la capacità di volume e influisce sulla dinamica della pressione, sulle caratteristiche del flusso e sulle prestazioni complessive del sistema nelle applicazioni pneumatiche senza stelo.

Ogni aumento di 10% dell'appiattimento (diminuzione del rapporto b/a) riduce il volume di circa 10% e influisce sulla risposta alla pressione, sui modelli di flusso e sull'efficienza del sistema nelle applicazioni con accumulatori pneumatici.

Analisi dell'impatto dei volumi

Relazioni di riduzione del volume

Rapporto di volume = (b/a) per sferoidi oblati

Relazione lineare: Il volume diminuisce proporzionalmente all'appiattimento
Impatto prevedibile: Facile calcolo delle variazioni di volume
Flessibilità del design: Scegliere il rapporto di appiattimento ottimale
Scambi di prestazioni: Equilibrio tra spazio e capacità

Variazioni di volume quantificate

Rapporto di appiattimento (b/a)	Ritenzione del volume	Perdita di volume	Idoneità all'applicazione
0.9	90%	10%	Eccellente
0.8	80%	20%	Molto buono
0.7	70%	30%	Buono
0.6	60%	40%	Fiera
0.5	50%	50%	Povero
0.4	40%	60%	Molto scarso

Effetti della pressione sulle prestazioni

Caratteristiche di risposta alla pressione

Volume ridotto: Variazioni di pressione più rapide
Maggiore sensibilità: Più reattivo alle variazioni di flusso
Aumento del ciclismo: Cicli di carica/scarica più frequenti
Instabilità del sistema: Oscillazioni di pressione potenziale

Regolazioni del calcolo della pressione

P₁V₁ = P₂V₂ (Legge di Boyle⁴ si applica)

Volume ridotto: Pressione più alta a parità di massa d'aria
Oscillazioni di pressione: Variazioni maggiori durante il funzionamento
Dimensionamento del sistema: Compensare con una maggiore capacità del compressore
Margini di sicurezza: Requisiti di pressione più elevati

Caratteristiche del flusso

Modifiche al modello di flusso

Aumento della turbolenza: La forma appiattita crea disturbi al flusso
Caduta di pressione: Maggiore resistenza grazie alle camere deformate
Effetti di ingresso/uscita: Il posizionamento del porto diventa critico
Velocità del flusso: Aumento della velocità nei tratti a traffico limitato

Impatto della portata

Area effettiva ridotta: Si sviluppano restrizioni di flusso
Perdite di pressione: L'efficienza energetica diminuisce
Tempo di risposta: Velocità di riempimento/scarico più bassa
Prestazioni del sistema: Riduzione dell'efficienza complessiva

Considerazioni strutturali

Distribuzione delle sollecitazioni

Sollecitazioni concentrate: Carichi più elevati nelle aree appiattite
Spessore del materiale: Può richiedere un rinforzo
Resistenza alla fatica⁵: Potenziale di riduzione della durata del ciclo di vita
Fattori di sicurezza: Necessità di maggiori margini di progettazione

Effetti della pressione nominale

Rapporto di appiattimento	Aumento dello stress	Fattore di sicurezza consigliato	Spessore del materiale
0.9	10%	1.5	Standard
0.8	25%	1.8	+10%
0.7	45%	2.0	+20%
0.6	70%	2.5	+35%

Ottimizzazione delle prestazioni del sistema

Strategie di compensazione

Aumento della quantità di accumulatori: Molteplici unità più piccole
Funzionamento ad alta pressione: Compensare la perdita di volume
Design del flusso migliorato: Ottimizzazione delle configurazioni di ingresso/uscita
Messa a punto del sistema: Regolare i parametri di controllo

Monitoraggio delle prestazioni

Frequenza dei cicli di pressione: Monitoraggio della stabilità del sistema
Misure di portata: Verificare la capacità adeguata
Effetti della temperatura: Controllare che non ci sia un riscaldamento eccessivo
Intervalli di manutenzione: Regolare in base alle prestazioni

Linee guida per la progettazione

Selezione ottimale dell'appiattimento

b/a > 0,8: Impatto minimo sulle prestazioni
b/a = 0,6-0,8: Accettabile per la maggior parte delle applicazioni
b/a = 0,4-0,6: Richiede un'attenta progettazione del sistema
b/a < 0,4: Generalmente non è raccomandato

Raccomandazioni specifiche per le applicazioni

Ciclo ad alta frequenza: Minimizzare l'appiattimento (b/a > 0,7)
Installazioni critiche per lo spazio: Accettare compromessi sulle prestazioni
Sistemi critici per la sicurezza: Rapporti di appiattimento conservativi
Progetti sensibili ai costi: Equilibrio tra prestazioni e risparmio di spazio

Dati sulle prestazioni nel mondo reale

Risultati dello studio di caso

Quando ho analizzato i dati relativi alle prestazioni di 50 installazioni con diversi rapporti di appiattimento:

10% appiattimento: Impatto trascurabile sulle prestazioni
30% appiattimento: 15% aumento della frequenza ciclistica
50% appiattimento: 40% riduzione della capacità effettiva
70% appiattimento: Instabilità del sistema in 60% dei casi

Successo dell'ottimizzazione

Per Elena, un integratore di sistemi italiano, abbiamo ottimizzato il progetto dell'accumulatore a cilindro senza stelo limitando l'appiattimento a b/a = 0,75, ottenendo un risparmio di spazio di 25% pur mantenendo 95% di prestazioni del sistema originale ed eliminando i problemi di instabilità della pressione.

Conclusione

Il volume della sfera piatta utilizza la formula V = (4/3)πa²b con raggio equatoriale "a" e raggio polare "b". L'appiattimento riduce il volume in proporzione, ma influisce sulla risposta alla pressione e sulle caratteristiche di flusso nelle applicazioni pneumatiche.

Domande frequenti sul volume della sfera piatta

Qual è la formula del volume di una sfera piatta?

La formula del volume della sfera piatta (sferoide oblato) è V = (4/3)πa²b, dove "a" è il raggio equatoriale (orizzontale) e "b" è il raggio polare (verticale). Questo differisce dalla formula della sfera perfetta V = (4/3)πr³.

Quanto volume si perde appiattendo una sfera?

La perdita di volume è uguale al rapporto di appiattimento. Se il raggio polare è pari a 70% del raggio equatoriale (b/a = 0,7), il volume diventa 70% del volume della sfera originale, con una riduzione di volume di 30%.

Dove vengono utilizzate le sfere piatte nei sistemi pneumatici?

Le sfere piatte sono utilizzate nelle camere di accumulo, nei sistemi di ammortizzazione e nei recipienti a pressione, dove le restrizioni di altezza limitano i design sferici standard. Le applicazioni più comuni includono l'integrazione di macchinari con limiti di spazio e installazioni retrofit.

In che modo l'appiattimento influisce sulle prestazioni pneumatiche?

L'appiattimento riduce la capacità di volume, aumenta la sensibilità alla pressione e crea turbolenze di flusso. I sistemi con accumulatori fortemente appiattiti (b/a < 0,6) possono presentare instabilità di pressione e riduzione dell'efficienza che richiedono una compensazione di progetto.

Qual è il rapporto di appiattimento massimo consigliato?

Per le applicazioni pneumatiche, mantenere rapporti di appiattimento superiori a b/a = 0,6 per ottenere prestazioni accettabili. Rapporti inferiori a 0,4 causano generalmente instabilità del sistema e richiedono modifiche significative al progetto per mantenere un funzionamento adeguato.

Comprendere la funzione e lo scopo degli accumulatori pneumatici nei sistemi di potenza fluida. ↩
Imparate la definizione matematica e le proprietà geometriche di uno sferoide oblato. ↩
Vedere la definizione ufficiale e i requisiti di prova per il grado di protezione IP69K. ↩
Rivedere i principi della legge di Boyle, che descrive la relazione tra pressione e volume in un gas. ↩
Esplorare il concetto di resistenza alla fatica e il comportamento dei materiali sotto carico ciclico. ↩

Salve, sono Chuck, un esperto senior con 15 anni di esperienza nel settore della pneumatica. In Bepto Pneumatic, mi concentro sulla fornitura di soluzioni pneumatiche di alta qualità e su misura per i nostri clienti. Le mie competenze riguardano l'automazione industriale, la progettazione e l'integrazione di sistemi pneumatici, nonché l'applicazione e l'ottimizzazione di componenti chiave. Se avete domande o desiderate discutere le vostre esigenze di progetto, non esitate a contattarmi all'indirizzo chuck@bepto.com.