
Vi è mai capitato di entrare in fabbrica e di essere colpiti dall'inconfondibile sibilo dei sistemi pneumatici? Quel rumore non è solo un fastidio, ma rappresenta uno spreco di energia, potenziali problemi normativi e un segnale di allarme per un funzionamento inefficiente.
Il rumore acustico nei sistemi pneumatici è generato da tre meccanismi principali: l'espansione del gas durante i rilasci di pressione, le vibrazioni meccaniche dei componenti e il flusso turbolento in tubi e raccordi. La comprensione di questi meccanismi consente agli ingegneri di implementare strategie mirate di riduzione del rumore che migliorano la sicurezza sul posto di lavoro, aumentano l'efficienza energetica e prolungano la durata delle apparecchiature.
Il mese scorso ho visitato un impianto di produzione farmaceutica nel New Jersey, dove il rumore eccessivo proveniente dalla loro cilindri senza stelo stava causando problemi a livello normativo. Il loro team aveva provato soluzioni generiche senza successo. Analizzando i meccanismi specifici di generazione del rumore, abbiamo ridotto il rumore del sistema di 14 dBA, portandolo da un rischio normativo a una situazione di conformità. Vi mostro come abbiamo fatto.
Indice dei contenuti
- Livello sonoro di espansione dei gas: Quale formula prevede il rumore dello scarico pneumatico?
- Spettro delle vibrazioni meccaniche: come può l'analisi di frequenza identificare le fonti di rumore?
- Perdita di inserzione del silenziatore: quali calcoli guidano la progettazione di un silenziatore efficace?
- Conclusione
- Domande frequenti sul rumore del sistema pneumatico
Livello sonoro di espansione dei gas: Quale formula prevede il rumore dello scarico pneumatico?
L'improvvisa espansione dell'aria compressa durante l'azionamento della valvola o lo scarico del cilindro crea una delle fonti di rumore più significative nei sistemi pneumatici. La comprensione della relazione matematica tra i parametri del sistema e la produzione di rumore è essenziale per una mitigazione efficace.
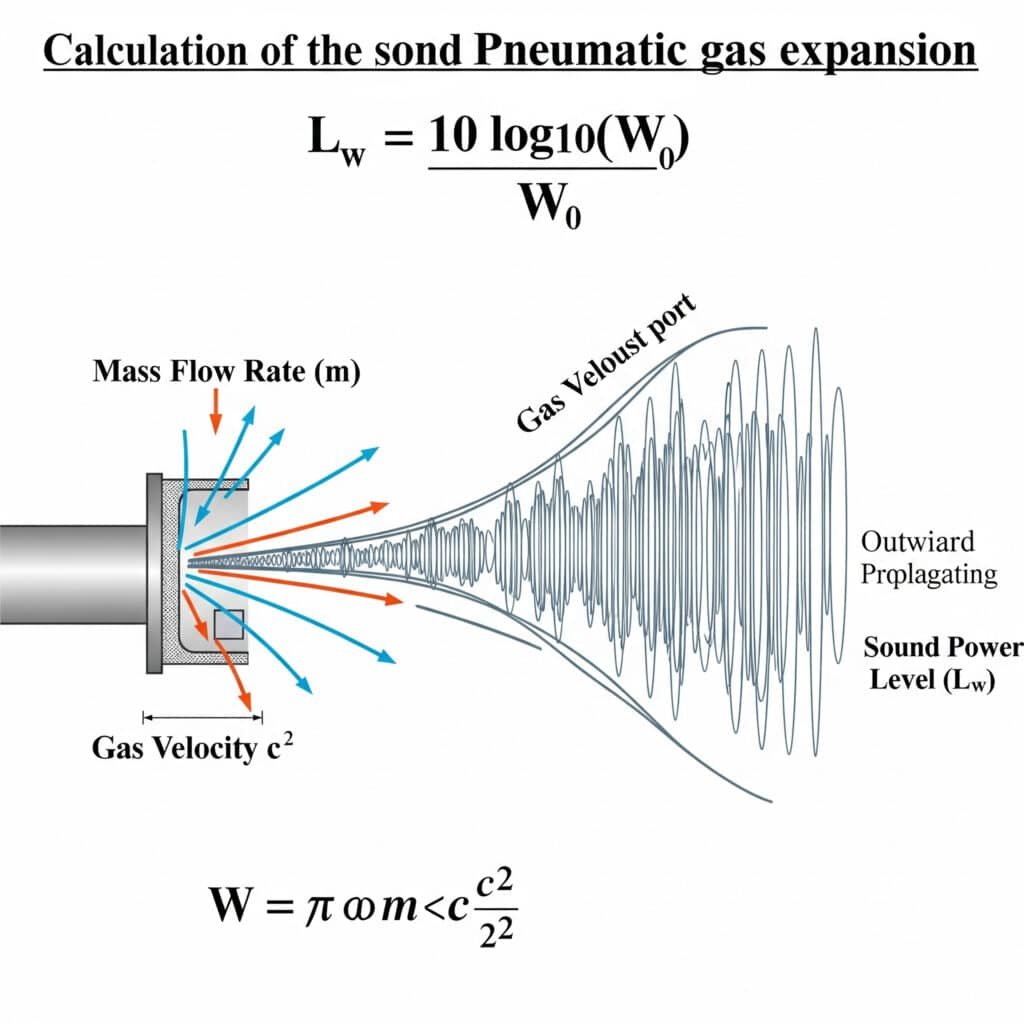
Il livello di potenza sonora derivante dall'espansione del gas può essere calcolato con la formula: Lw = 10 log₁₀(W/W₀), dove W è la potenza acustica in watt e W₀ è la potenza di riferimento (10-¹² watt). Per i sistemi pneumatici, W può essere stimato come W = η × m × (c²/2), dove η è l'efficienza acustica, m è la portata massica e c è la velocità del gas.
Ricordo la risoluzione di un problema in una linea di confezionamento in Illinois, dove i livelli di rumore superavano i 95 dBA, ben al di sopra del livello di rumore. Limiti OSHA1. Il team di manutenzione si era concentrato sulle fonti meccaniche, ma la nostra analisi ha rivelato che 70% del rumore proveniva dalle porte di scarico. Applicando la formula di espansione del gas, abbiamo individuato che la pressione di esercizio era superiore di 2,2 bar rispetto al necessario, creando un rumore di scarico eccessivo. Questa semplice regolazione della pressione ha ridotto il rumore di 8 dBA senza influire sulle prestazioni.
Equazioni fondamentali del rumore di espansione del gas
Analizziamo le formule chiave per prevedere il rumore di espansione:
Calcolo della potenza sonora
La potenza acustica generata dal gas in espansione può essere calcolata come:
W = η × m × (c²/2)
Dove:
- W = Potenza acustica (watt)
- η = Efficienza acustica (tipicamente 0,001-0,01 per gli scarichi pneumatici)
- m = portata massica (kg/s)
- c = Velocità del gas allo scarico (m/s)
Il livello di potenza sonora in decibel è quindi il seguente:
Lw = 10 log₁₀(W/W₀)
Dove W₀ è la potenza di riferimento di 10-¹² watt.
Determinazione della portata massica
La portata massica attraverso un orifizio può essere calcolata come:
m = Cd × A × p₁ × √(2γ/(γ-1) × (RT₁) × [(p₂/p₁)^(2/γ) - (p₂/p₁)^((γ+1)/γ)])
Dove:
- Cd = Coefficiente di scarico (in genere 0,6-0,8)
- A = Area dell'orifizio (m²)
- p₁ = Pressione assoluta a monte (Pa)
- p₂ = Pressione assoluta a valle (Pa)
- γ = Rapporto di calore specifico (1,4 per l'aria)
- R = costante dei gas per l'aria (287 J/kg-K)
- T₁ = Temperatura a monte (K)
Per il flusso strozzato (comune negli scarichi pneumatici), questo si semplifica in:
m = Cd × A × p₁ × √(γ/(RT₁)) × (2/(γ+1))^((γ+1)/(2(γ-1))
Fattori che influenzano il rumore dell'espansione del gas
| Fattore | Impatto sul livello di rumore | Approccio di mitigazione |
|---|---|---|
| Pressione di esercizio | Aumento di 3-4 dBA per barra | Ridurre la pressione del sistema al minimo richiesto |
| Dimensioni dell'attacco di scarico | Le porte più piccole aumentano la velocità e il rumore | Utilizzare porte di dimensioni adeguate ai requisiti di portata |
| Temperatura di scarico | Le temperature più elevate aumentano la rumorosità | Consentire il raffreddamento prima dell'espansione, ove possibile |
| Rapporto di espansione | Rapporti più alti creano più rumore | Espansione del palcoscenico attraverso più fasi |
| Portata | Il raddoppio del flusso aumenta il rumore di ~3 dBA | Utilizzare più scarichi piccoli invece di uno grande |
Esempio pratico di previsione del rumore
Per un tipico cilindro senza stelo con:
- Pressione di esercizio: 6 bar (600.000 Pa)
- Diametro della porta di scarico: 4 mm (area = 1,26 × 10-⁵ m²)
- Coefficiente di scarico: 0,7
- Efficienza acustica: 0,005
La portata massica durante lo scarico sarebbe approssimativamente:
m = 0,7 × 1,26 × 10-⁵ × 600.000 × 0,0404 = 0,0214 kg/s
Assumendo una velocità di scarico di 343 m/s (velocità sonica), la potenza acustica sarebbe:
W = 0,005 × 0,0214 × (343²/2) = 6,29 Watt
Il livello di potenza sonora risultante:
Lw = 10 log₁₀(6,29/10-¹²) = 128 dB
Questo elevato livello di potenza sonora spiega perché gli scarichi pneumatici non silenziati sono fonti di rumore così importanti negli ambienti industriali.
Spettro delle vibrazioni meccaniche: come può l'analisi di frequenza identificare le fonti di rumore?
Le vibrazioni meccaniche nei componenti pneumatici generano segnali di rumore distintivi che possono essere analizzati per individuare problemi specifici. L'analisi dello spettro di frequenza fornisce la chiave per identificare e risolvere queste fonti di rumore meccanico.
Le vibrazioni meccaniche nei sistemi pneumatici producono rumore con spettri di frequenza caratteristici che possono essere analizzati utilizzando Trasformata veloce di Fourier (FFT)2 tecniche. Le gamme di frequenza principali comprendono le vibrazioni strutturali a bassa frequenza (10-100 Hz), le armoniche operative a media frequenza (100-1000 Hz) e le vibrazioni ad alta frequenza indotte dal flusso (1-10 kHz), ognuna delle quali richiede approcci di mitigazione diversi.
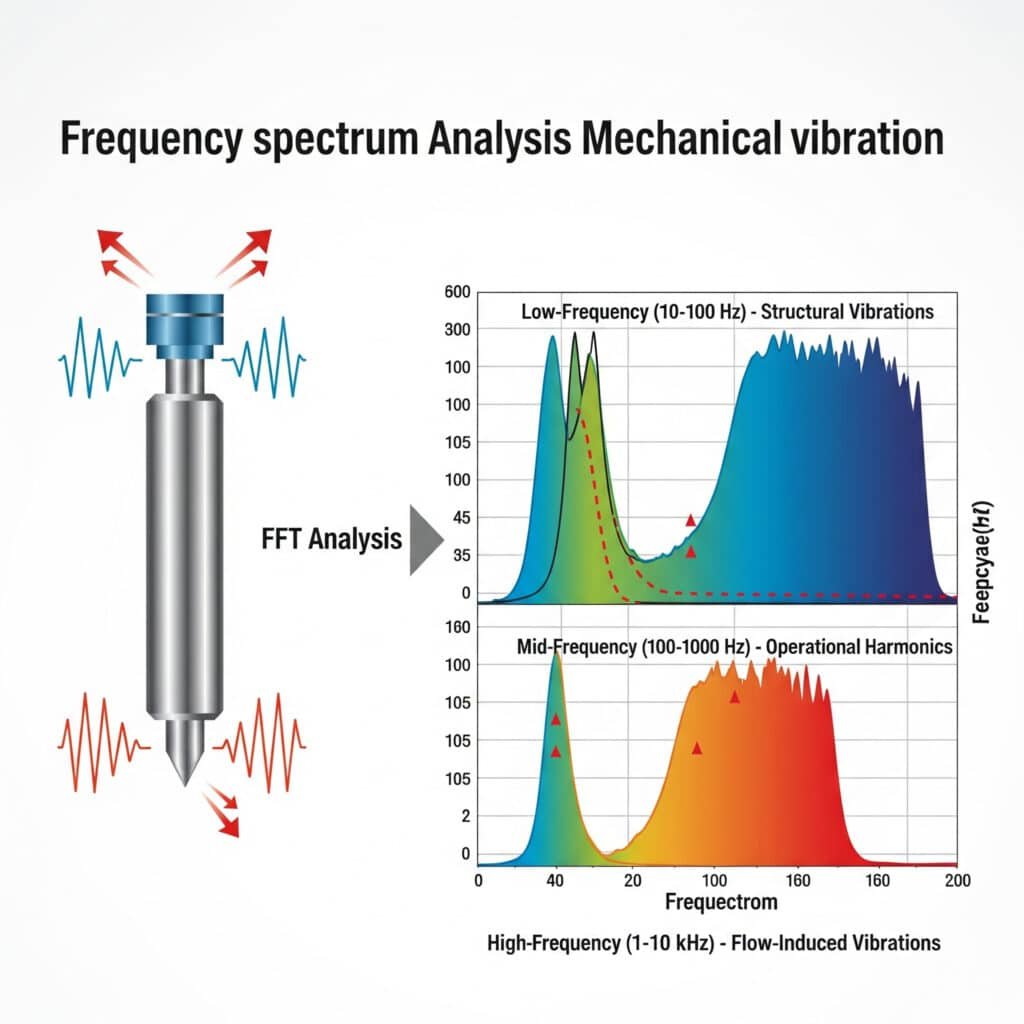
Durante una consulenza presso un produttore di componenti automobilistici del Michigan, il team di manutenzione era alle prese con un rumore eccessivo proveniente da un sistema di trasferimento di cilindri senza stelo. La risoluzione dei problemi convenzionali non era riuscita a identificare la fonte. La nostra analisi dello spettro delle vibrazioni ha rivelato un picco distinto a 237 Hz, che corrisponde esattamente alla risonanza della banda di tenuta interna del cilindro. Modificando il sistema di montaggio per smorzare questa frequenza specifica, abbiamo ridotto il rumore di 11 dBA senza alcuna interruzione della produzione.
Metodologia di analisi dello spettro di frequenza
Un'analisi efficace delle vibrazioni segue un approccio sistematico:
- Impostazione della misura: Utilizzo di accelerometri e microfoni acustici
- Acquisizione dei dati: Acquisizione di segnali di vibrazione nel dominio del tempo
- Analisi FFT: Conversione nel dominio della frequenza
- Mappatura spettrale: Identificazione delle frequenze caratteristiche
- Fonte Attribuzione: Abbinamento delle frequenze a componenti specifici
Gamme di frequenza caratteristiche nei sistemi pneumatici
| Gamma di frequenza | Fonti tipiche | Caratteristiche acustiche |
|---|---|---|
| 10-50 Hz | Risonanza strutturale, problemi di montaggio | Rumore a bassa frequenza, sentito più che udito |
| 50-200 Hz | Urti del pistone, azionamento della valvola | Un forte rumore o un colpo di martelletto |
| 200-500 Hz | Attrito delle guarnizioni, risonanza interna | Ronzio o ronzio a media frequenza |
| 500-2000 Hz | Turbolenza del flusso, pulsazioni di pressione | Sibili con componenti tonali |
| 2-10 kHz | Perdite, flusso ad alta velocità | Sibili acuti, molto fastidiosi per l'orecchio umano |
| >10 kHz | Micro-turbolenza, espansione del gas | Componenti a ultrasuoni, indicatore di perdita di energia |
Percorsi di trasmissione delle vibrazioni
Il rumore delle vibrazioni meccaniche segue molteplici percorsi:
Trasmissione per via strutturale
Le vibrazioni attraversano i componenti solidi:
- Il componente vibra a causa delle forze interne
- Trasferimento delle vibrazioni attraverso i punti di montaggio
- Le strutture collegate amplificano e irradiano il suono
- Le grandi superfici fungono da efficienti radiatori acustici
Trasmissione aerea
Radiazione diretta del suono da superfici vibranti:
- La vibrazione della superficie sposta l'aria
- Lo spostamento crea onde di pressione
- Le onde si propagano nell'aria
- La dimensione della superficie radiante determina l'efficienza
Caso di studio: Analisi delle vibrazioni dei cilindri senza stelo
Per un cilindro magnetico senza stelo che presenta un rumore eccessivo:
| Frequenza (Hz) | Ampiezza (dB) | Identificazione della fonte | Strategia di mitigazione |
|---|---|---|---|
| 43 | 78 | Risonanza di montaggio | Staffa di montaggio irrigidita |
| 86 | 65 | Armonica di risonanza di montaggio | Indirizzato alla risonanza primaria |
| 237 | 91 | Risonanza della banda di tenuta | Aggiunta di materiale smorzante al corpo del cilindro |
| 474 | 83 | Armonica della banda di tenuta | Indirizzato alla risonanza primaria |
| 1250 | 72 | Turbolenza del flusso d'aria | Design modificato della porta |
| 3700 | 68 | Perdite sui tappi di chiusura | Guarnizioni sostituite |
Le strategie di mitigazione combinate hanno ridotto il rumore complessivo di 14 dBA, con il miglioramento più significativo derivante dalla risoluzione della risonanza a 237 Hz.
Tecniche avanzate di analisi delle vibrazioni
Oltre all'analisi FFT di base, diverse tecniche avanzate forniscono approfondimenti:
Analisi dell'ordine
Particolarmente utile per i sistemi a velocità variabile:
- Tracce di frequenze che scalano con la velocità operativa
- Separa le componenti dipendenti dalla velocità da quelle a frequenza fissa
- Identifica i problemi relativi a specifiche fasi del movimento
Analisi della forma di deflessione operativa (ODS)
Mappatura degli schemi di vibrazione dell'intero sistema:
- Più punti di misurazione creano una "mappa" delle vibrazioni
- Rivela come si muovono le strutture durante il funzionamento
- Identifica le posizioni ottimali per i trattamenti di smorzamento
Analisi modale
Determina le frequenze naturali e le forme di modo:
- Identifica le frequenze di risonanza prima dell'uso.
- Prevede le frequenze dei potenziali problemi
- Guida alle modifiche strutturali per evitare la risonanza
Perdita di inserzione del silenziatore: quali calcoli guidano la progettazione di un silenziatore efficace?
Silenziatori e silenziatori sono fondamentali per ridurre il rumore del sistema pneumatico, ma la loro progettazione deve basarsi su calcoli di ingegneria acustica per garantire l'efficacia senza compromettere le prestazioni del sistema.
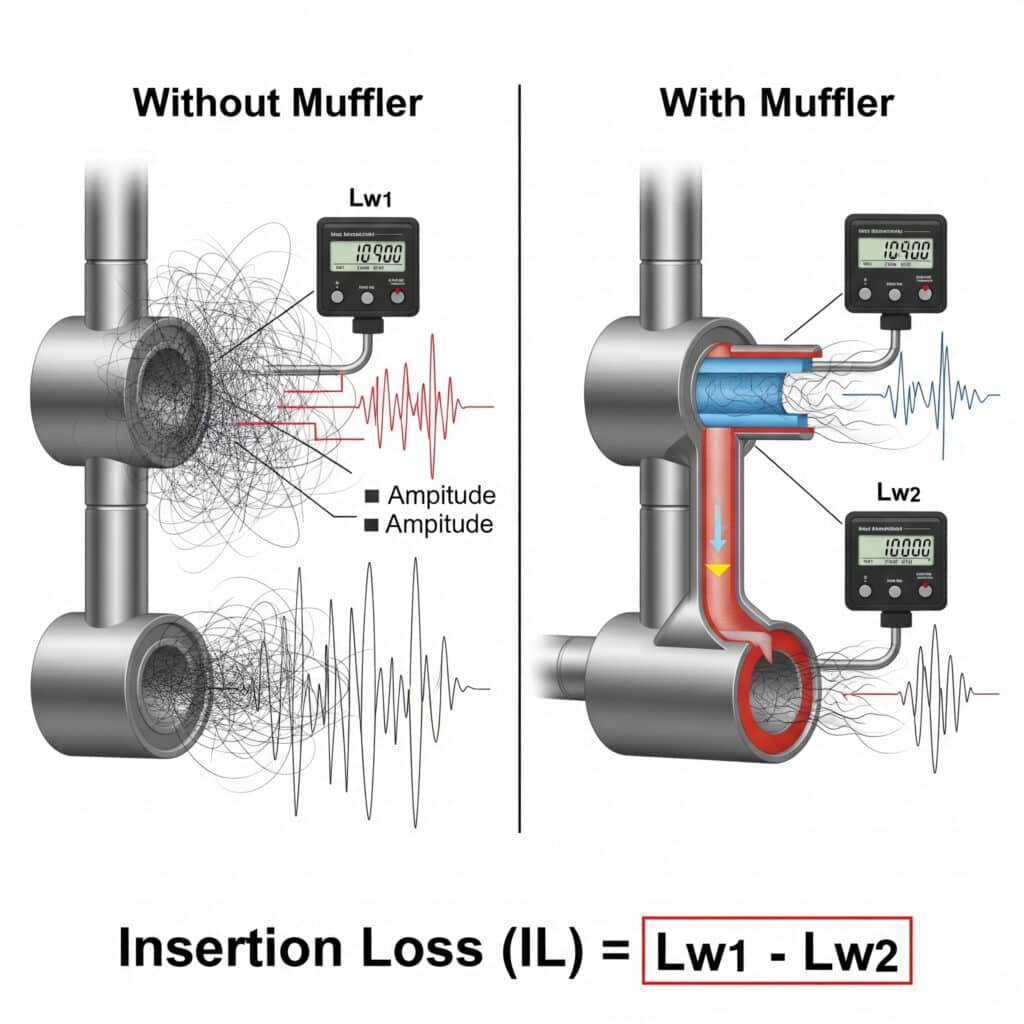
Silenziatore perdita di inserzione3 (IL) quantifica l'efficacia della riduzione del rumore e può essere calcolato come IL = Lw₁ - Lw₂, dove Lw₁ è il livello di potenza sonora senza silenziatore e Lw₂ è il livello con il silenziatore installato. Per i sistemi pneumatici, i silenziatori efficaci raggiungono in genere una perdita di inserzione di 15-30 dB nell'intervallo di frequenza critico da 500 Hz a 4 kHz, mantenendo una contropressione accettabile.
Di recente ho aiutato un produttore di dispositivi medici del Massachusetts a risolvere un problema di rumorosità con il suo sistema di cilindri di precisione senza stelo. Il loro tentativo iniziale di utilizzare silenziatori non disponibili sul mercato riduceva il rumore, ma creava una contropressione eccessiva che influiva sui tempi di ciclo. Calcolando la perdita di inserzione necessaria su bande di frequenza specifiche e progettando un silenziatore multicamera personalizzato, abbiamo ottenuto una riduzione del rumore di 24 dB con un impatto minimo sulle prestazioni. Il risultato è stato un sistema che ha soddisfatto i requisiti di rumorosità e precisione.
Fondamenti della perdita di inserzione dei silenziatori
L'equazione del nucleo per la perdita di inserzione è:
IL = Lw₁ - Lw₂
Dove:
- IL = Perdita di inserzione (dB)
- Lw₁ = Livello di potenza sonora senza silenziatore (dB)
- Lw₂ = Livello di potenza sonora con silenziatore (dB)
Per l'analisi specifica della frequenza, questo diventa:
IL(f) = Lw₁(f) - Lw₂(f)
Dove f indica la banda di frequenza specifica analizzata.
Parametri di progettazione del silenziatore e loro effetti
| Parametro | Effetto sulla perdita di inserzione | Effetto sulla contropressione | Intervallo ottimale |
|---|---|---|---|
| Volume della camera | Un volume più grande aumenta l'IL alle basse frequenze | Impatto minimo se progettato correttamente | 10-30× volume del condotto di scarico |
| Numero di camere | Un maggior numero di camere aumenta l'IL alle medie frequenze | Aumenta con un numero maggiore di camere | 2-4 camere per la maggior parte delle applicazioni |
| Rapporto di espansione | Rapporti più alti migliorano l'IL | Impatto minimo se graduale | Rapporto di superficie da 4:1 a 16:1 |
| Materiale acustico | Migliora l'IL ad alta frequenza | Impatto minimo con un design adeguato | Spessore 10-50 mm |
| Perforazione del deflettore | Influenza le medie frequenze IL | Impatto significativo | 30-50% area aperta |
| Lunghezza del percorso di flusso | I percorsi più lunghi migliorano l'IL a bassa frequenza | Aumenta con la lunghezza | 3-10× diametro della porta |
Modelli teorici per la previsione della perdita di inserzione
Diversi modelli possono prevedere la perdita di inserzione per diversi tipi di silenziatore:
Modello di camera di espansione
Per camere di espansione semplici:
IL = 10 log₁₀[1 + 0,25(m-1/m)² sin²(kL)]
Dove:
- m = Rapporto d'area (area della camera / area del tubo)
- k = numero d'onda (2πf/c, dove f è la frequenza e c la velocità del suono)
- L = lunghezza della camera
Modello di silenziatore dissipativo
Per marmitte con materiali fonoassorbenti:
IL = 8,68α(L/d)
Dove:
- α = coefficiente di assorbimento del materiale
- L = Lunghezza della sezione rivestita
- d = diametro del percorso del flusso
Modello di silenziatore reattivo (Risonatore di Helmholtz4)
Per i silenziatori a risonanza:
IL = 10 log₁₀[1 + (ρc/2S)² × (V/L'c²) × ω²/((ω₀² - ω²)² + (Rω/ρc)²)]
Dove:
- ρ = densità dell'aria
- c = velocità del suono
- S = Area della sezione trasversale del collo
- V = Volume della cavità
- L' = Lunghezza effettiva del collo
- ω = Frequenza angolare
- ω₀ = Frequenza di risonanza
- R = Resistenza acustica
Processo pratico di selezione delle marmitte
Selezionare o progettare un silenziatore appropriato:
- Misura dello spettro di rumore: Determinare il contenuto di frequenza del rumore
- Calcolo dell'IL richiesto: Determinare la riduzione necessaria in base alla frequenza
- Valutare i requisiti di flusso: Calcolo della contropressione massima consentita
- Selezionare il tipo di silenziatore:
- Reattivo (camere di espansione) per le basse frequenze
- Dissipativo (assorbente) per le alte frequenze
- Combinazione per il rumore a banda larga - Verifica delle prestazioni: Test della perdita di inserzione e della contropressione
Considerazioni sulla contropressione
Una contropressione eccessiva può avere un impatto significativo sulle prestazioni del sistema:
Calcolo della contropressione
La contropressione può essere stimata come:
ΔP = ρ(Q/Cd×A)²/2
Dove:
- ΔP = Perdita di carico (Pa)
- ρ = densità dell'aria (kg/m³)
- Q = Portata (m³/s)
- Cd = Coefficiente di scarico
- A = Area di flusso effettiva (m²)
Valutazione dell'impatto sulle prestazioni
Per un cilindro senza stelo con:
- Diametro del foro: 40 mm
- Corsa: 500 mm
- Tempo di ciclo: 2 secondi
- Pressione di esercizio: 6 bar
Ogni 0,1 bar di contropressione:
- Riduzione della forza erogata di circa 1,7%
- Aumento del tempo di ciclo di circa 2,3%
- Aumento del consumo energetico di circa 1,5%
Caso di studio: Design personalizzato della marmitta
Per un'applicazione di precisione di cilindri senza stelo con requisiti di rumorosità rigorosi:
| Parametro | Condizione iniziale | Silenziatore di serie | Design personalizzato |
|---|---|---|---|
| Livello sonoro | 89 dBA | 76 dBA | 65 dBA |
| Retropressione | 0,05 bar | 0,42 bar | 0,11 bar |
| Tempo di ciclo | 1,8 secondi | 2,3 secondi | 1,9 secondi |
| Risposta in frequenza | Banda larga | Scarsa a 2-4 kHz | Ottimizzato su tutto lo spettro |
| Vita utile | N/D | 3 mesi (intasamento) | >12 mesi |
| Costo di implementazione | N/D | $120 per punto | $280 per punto |
Il design personalizzato del silenziatore ha consentito di ottenere una riduzione del rumore superiore, mantenendo al contempo prestazioni accettabili del sistema, con un periodo di ritorno dell'investimento inferiore a 6 mesi se si considerano i miglioramenti della produttività.
Conclusione
La comprensione dei meccanismi di generazione del rumore acustico - livelli sonori di espansione del gas, spettri delle vibrazioni meccaniche e calcolo della perdita di inserzione dei silenziatori - fornisce le basi per un efficace controllo del rumore nei sistemi pneumatici. Applicando questi principi, è possibile creare sistemi pneumatici più silenziosi, più efficienti e più affidabili, garantendo al contempo la conformità alle normative e migliorando le condizioni del luogo di lavoro.
Domande frequenti sul rumore del sistema pneumatico
Quali sono i limiti OSHA per l'esposizione al rumore dei sistemi pneumatici?
L'OSHA limita l'esposizione al rumore sul luogo di lavoro a 90 dBA per una media ponderata nel tempo di 8 ore, con un tasso di cambio di 5 dBA. Tuttavia, il limite di esposizione raccomandato dal NIOSH è più prudente, pari a 85 dBA. I sistemi pneumatici superano spesso questi limiti, con scarichi non silenziati che spesso generano 90-110 dBA a un metro di distanza, richiedendo controlli ingegneristici per la conformità.
In che modo la pressione di esercizio influisce sulla rumorosità del sistema pneumatico?
La pressione di esercizio ha un impatto significativo sulla generazione di rumore: ogni aumento di pressione di 1 bar aggiunge in genere 3-4 dBA ai livelli di rumore di scarico. Questa relazione è logaritmica piuttosto che lineare, poiché la potenza sonora aumenta con il quadrato del rapporto di pressione. La riduzione della pressione del sistema al minimo richiesto per il funzionamento è spesso la strategia di riduzione del rumore più semplice ed economica.
Qual è la differenza tra silenziatori reattivi e dissipativi per i sistemi pneumatici?
I silenziatori reattivi utilizzano camere e passaggi per riflettere le onde sonore e creare interferenze distruttive, rendendoli efficaci per i rumori a bassa frequenza (sotto i 500 Hz) con una perdita di pressione minima. I silenziatori dissipativi utilizzano materiali fonoassorbenti per convertire l'energia acustica in calore, rendendoli più efficaci per i rumori ad alta frequenza (sopra i 500 Hz) ma più suscettibili alla contaminazione. Molti silenziatori pneumatici industriali combinano entrambi i principi per una riduzione del rumore a banda larga.
Come posso identificare la fonte di rumore dominante nel mio sistema pneumatico?
Utilizzate un approccio sistematico a partire dai test operativi: fate funzionare il sistema a diverse pressioni, velocità e carichi, misurando il rumore. Quindi eseguire l'isolamento dei componenti facendo funzionare i singoli elementi separatamente. Infine, condurre un'analisi di frequenza utilizzando un fonometro con capacità di banda d'ottava: le basse frequenze (50-250 Hz) indicano in genere problemi strutturali, le medie frequenze (250-2000 Hz) suggeriscono un rumore operativo e le alte frequenze (2-10 kHz) indicano problemi di flusso o di perdita.
Qual è la relazione tra il livello di rumore e la distanza da un componente pneumatico?
Il rumore dei componenti pneumatici segue la legge quadratica inversa in condizioni di campo libero, diminuendo di circa 6 dB ogni volta che la distanza raddoppia. Tuttavia, nei tipici ambienti industriali con superfici riflettenti, la riduzione effettiva è spesso di soli 3-4 dB al raddoppio della distanza a causa del riverbero. Ciò significa che il raddoppio della distanza da una sorgente di rumore di 90 dB potrebbe ridurre il livello solo a 86-87 dB, anziché agli 84 dB teorici.
-
Fornisce le normative ufficiali dell'Occupational Safety and Health Administration (OSHA) e i limiti di esposizione ammissibili (PEL) per il rumore sul posto di lavoro, che è un fattore chiave per la mitigazione acustica. ↩
-
Spiega l'algoritmo della Trasformata veloce di Fourier (FFT), uno strumento matematico fondamentale utilizzato per convertire un segnale nel dominio del tempo (come una vibrazione o un'onda sonora) nelle sue componenti di frequenza per l'analisi. ↩
-
Descrive l'analisi modale, una tecnica ingegneristica avanzata utilizzata per determinare le proprietà dinamiche intrinseche di un sistema, come le frequenze naturali e le forme di modo, per prevedere ed evitare la risonanza. ↩
-
Offre una spiegazione dettagliata della perdita di inserzione (IL), il parametro principale utilizzato per quantificare le prestazioni di una marmitta o di un silenziatore misurando la riduzione del livello sonoro che fornisce. ↩


