
Hebt u ooit mysterieuze trillingen opgemerkt in uw pneumatische leidingen? Of onverklaarbare krachtvariaties in uw cilinders ondanks een stabiele toevoerdruk? Deze verschijnselen zijn niet willekeurig: ze zijn het resultaat van drukgolven die zich door uw systeem voortplanten en effecten veroorzaken die kunnen variëren van kleine inefficiënties tot rampzalige storingen.
Drukschommelingen in pneumatische systemen zijn golfverschijnselen die zich voortplanten met snelheden die de snelheid van geluid1en creëert dynamische effecten zoals resonantie, staande golven2en drukversterking. Inzicht in deze fluctuaties is cruciaal omdat ze kunnen leiden tot vermoeidheid van componenten, instabiliteit van de besturing en energieverliezen van 10-25% in typische industriële systemen3.
Vorige maand gaf ik advies aan een assemblagefabriek in Tennessee waar een kritisch pneumatisch klemsysteem last had van intermitterende krachtvariaties ondanks een stabiele toevoerdruk. Het onderhoudsteam had kleppen, regelaars en zelfs het hele luchtbereidingsunit4 zonder succes. Door de dynamica van de drukgolven te analyseren - in het bijzonder de staande golfpatronen in hun toevoerleidingen - stelden we vast dat ze op een frequentie werkten die destructieve interferentie bij de cilinder veroorzaakte. Een eenvoudige aanpassing aan de lengte van hun leidingen maakte een einde aan het probleem en bespaarde hen weken productievertraging. Ik zal u laten zien hoe inzicht in de drukschommelingstheorie de betrouwbaarheid van uw pneumatisch systeem kan veranderen.
Inhoudsopgave
- Golfvoortplantingssnelheid: Hoe snel verplaatsen drukstoringen zich in uw systeem?
- Verificatie van staande golven: Hoe zorgen resonante frequenties voor prestatieproblemen?
- Pulsverzwakkingsmethoden: Welke technieken dempen effectief destructieve drukschommelingen?
- Conclusie
- Veelgestelde vragen over drukschommelingen in pneumatische systemen
Golfvoortplantingssnelheid: Hoe snel verplaatsen drukstoringen zich in uw systeem?
Begrijpen hoe snel drukstoringen zich voortplanten door pneumatische systemen is fundamenteel voor het voorspellen en beheersen van hun effecten. De voortplantingssnelheid bepaalt de reactietijd van het systeem, de resonantiefrequenties en het potentieel voor destructieve interferentie.
Drukgolven in pneumatische systemen verplaatsen zich met de geluidssnelheid in het gasmedium, die kan worden berekend met de formule c = √(γRT), waarbij γ de specifieke warmteverhouding is, R de specifieke gasconstante en T de absolute temperatuur. Voor lucht van 20°C komt dit overeen met ongeveer 343 m/s, hoewel deze snelheid wordt gewijzigd door factoren zoals de elasticiteit van de pijp, de samendrukbaarheid van het gas en de stromingsomstandigheden.
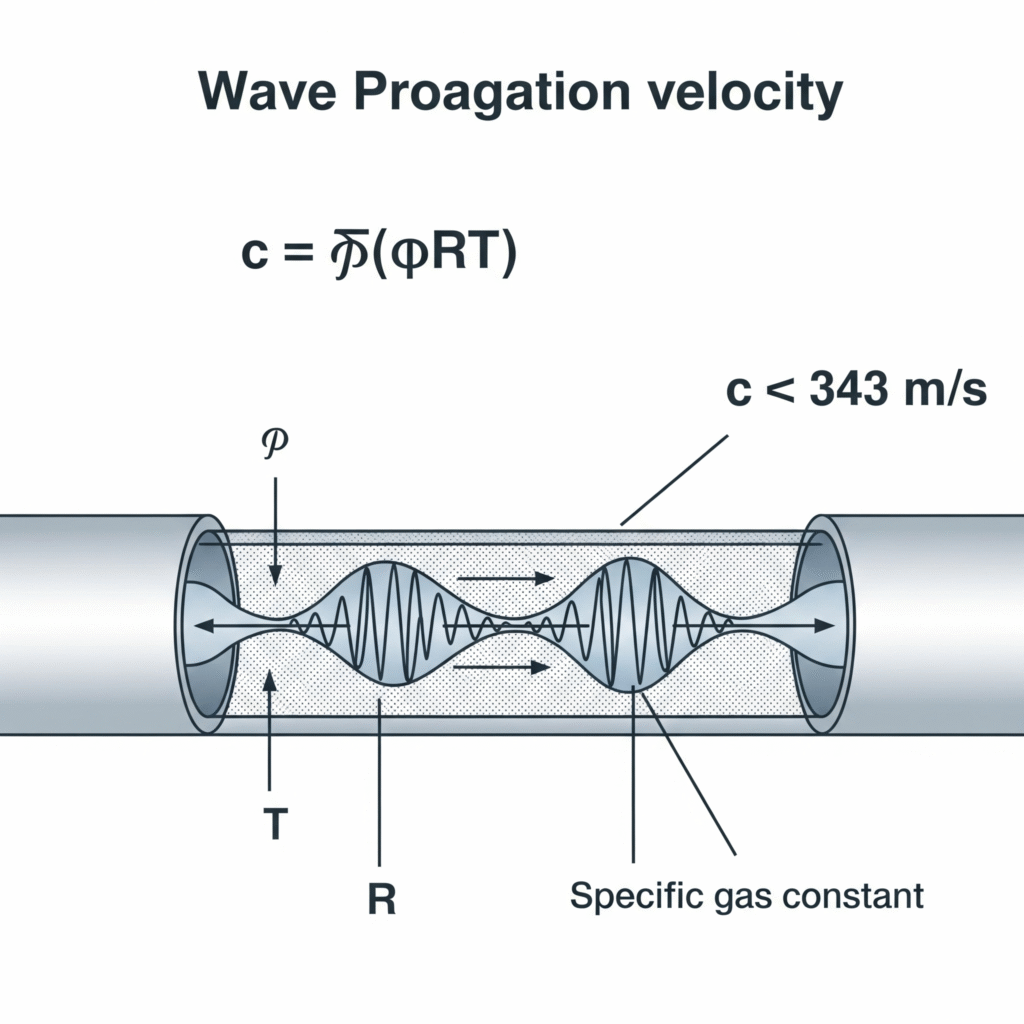
Onlangs heb ik geholpen bij het oplossen van problemen met een precisie-assemblagemachine in Zwitserland waar pneumatische grijpers een vertraging van 12 ms hadden tussen activering en krachtuitoefening - een eeuwigheid in een productieomgeving met hoge snelheid. Hun ingenieurs waren uitgegaan van onmiddellijke drukoverdracht. Door de werkelijke voortplantingssnelheid van de golven in hun systeem (328 m/s) te meten en rekening te houden met de lijnlengte van 4 meter, berekenden we een theoretische transmissietijd van 12,2 ms - bijna exact gelijk aan de waargenomen vertraging. Door de kleppen dichter bij de actuators te plaatsen, werd deze vertraging teruggebracht tot 3 ms en steeg de productiesnelheid met 14%.
Fundamentele golfsnelheidsvergelijkingen
De basisvergelijking voor de voortplantingssnelheid van drukgolven in een gas is:
c = √(γRT)
Waar:
- c = Golfvoortplantingssnelheid (m/s)
- γ = Specifieke warmteverhouding (1,4 voor lucht)
- R = Specifieke gasconstante (287 J/kg-K voor lucht)
- T = absolute temperatuur (K)
Voor lucht bij 20°C (293K) geeft dit:
c = √(1,4 × 287 × 293) = 343 m/s
Gewijzigde golfsnelheid in pneumatische leidingen
In echte pneumatische systemen wordt de effectieve golfsnelheid gewijzigd door de elasticiteit van de pijp en andere factoren volgens de formule:
c_eff = c / √(1 + (Dψ/Eh))
Waar:
- c_eff = effectieve golfsnelheid (m/s)
- D = diameter buis (m)
- ψ = samendrukbaarheidsfactor van gas
- E = elasticiteitsmodulus van buismateriaal (Pa)
- h = wanddikte van de pijp (m)
Effecten van temperatuur en druk op golfsnelheid
De golfsnelheid varieert afhankelijk van de bedrijfsomstandigheden:
| Temperatuur | Druk | Golfsnelheid in lucht | Praktische implicaties |
|---|---|---|---|
| 0°C (273K) | 1 bar | 331 m/s | Langzamere reactie in koude omgevingen |
| 20°C (293K) | 1 bar | 343 m/s | Standaard referentievoorwaarde |
| 40°C (313K) | 1 bar | 355 m/s | Snellere respons in warme omgevingen |
| 20°C (293K) | 6 bar | 343 m/s* | Druk heeft minimaal direct effect op snelheid |
*Opmerking: Hoewel de basisgolfsnelheid onafhankelijk is van de druk, kan de effectieve snelheid in echte systemen worden beïnvloed door drukgeïnduceerde veranderingen in de elasticiteit van de pijp en het gedrag van het gas.
Praktische berekening van golfvoortplantingstijd
Voor een pneumatisch systeem met:
- Lijnlengte (L): 5 meter
- Bedrijfstemperatuur: 20°C (c = 343 m/s)
- Materiaal pijp: Buizen van polyurethaan (wijzigt de snelheid met ongeveer 5%)
De effectieve golfsnelheid zou zijn:
c_eff = 343 × 0,95 = 326 m/s
En de voortplantingstijd van de golf zou zijn:
t = L/c_eff = 5/326 = 0,0153 seconden (15,3 milliseconden)
Dit is de minimale tijd die een drukverandering nodig heeft om van het ene uiteinde van de leiding naar het andere uiteinde te gaan - een kritieke factor in toepassingen met hoge snelheden.
Metingstechnieken voor golfsnelheid
Er kunnen verschillende methoden worden gebruikt om de werkelijke golfsnelheid in pneumatische systemen te meten:
Methode met dubbele druksensor
- Installeer druksensoren op bekende afstanden van elkaar
- Creëer een drukpuls (snelle klepopening)
- Tijdvertraging meten tussen drukstijging bij elke sensor
- Bereken snelheid als afstand gedeeld door tijdvertraging
Methode voor resonantiefrequentie
- Drukschommelingen creëren in een gesloten buis
- Meet de fundamentele resonantiefrequentie (f)
- Bereken de snelheid met c = 2Lf voor een buis met een gesloten uiteinde
- Controleer met harmonischen (oneven veelvouden van de grondtoon)
Reflectie Timing Methode
- Installeer een druksensor in de buurt van een ventiel
- Creëer een drukpuls door de klep snel te openen
- Meet de tijd tussen de eerste puls en de gereflecteerde puls
- Bereken snelheid als 2L gedeeld door de reflectietijd
Casestudie: Invloed van golfsnelheid op systeemrespons
Voor een robot eindeffector met pneumatische grijpers:
| Parameter | Origineel ontwerp (5m lijnen) | Geoptimaliseerd ontwerp (1m lijnen) | Verbetering |
|---|---|---|---|
| Lijnlengte | 5 meter | 1 meter | 80% reductie |
| Golfvoortplantingstijd | 15,3 ms | 3,1 ms | 12,2 ms sneller |
| Drukopbouwtijd | 28 ms | 9 ms | 19 ms sneller |
| Stabiliteit greepkracht | ±12% variatie | ±3% variatie | 75% verbetering |
| Cyclustijd | 1,2 seconden | 0,95 seconden | 21% sneller |
| Productie | 3000 onderdelen/uur | 3780 onderdelen/uur | 26% toename |
Deze casestudie laat zien hoe het begrijpen en optimaliseren van golfvoortplanting de systeemprestaties aanzienlijk kan beïnvloeden.
Verificatie van staande golven: Hoe zorgen resonante frequenties voor prestatieproblemen?
Staande golven ontstaan wanneer drukgolven reflecteren en met zichzelf interfereren, waardoor vaste patronen van drukknooppunten en antinodes ontstaan. Deze resonantieverschijnselen kunnen ernstige prestatieproblemen veroorzaken in pneumatische systemen als ze niet goed worden begrepen en beheerd.
Staande golven in pneumatische systemen ontstaan wanneer drukgolven reflecteren op grenzen en constructief interfereren, waardoor resonantiefrequenties ontstaan waar drukfluctuaties worden versterkt. Deze resonanties volgen de formule f = nc/2L voor gesloten buizen, waarbij n het harmonische getal is, c de golfsnelheid en L de buislengte. Experimentele verificatie met behulp van druksensoren, versnellingsmeters en akoestische metingen bevestigt deze theoretische voorspellingen en leidt tot effectieve strategieën om de druk te verminderen.
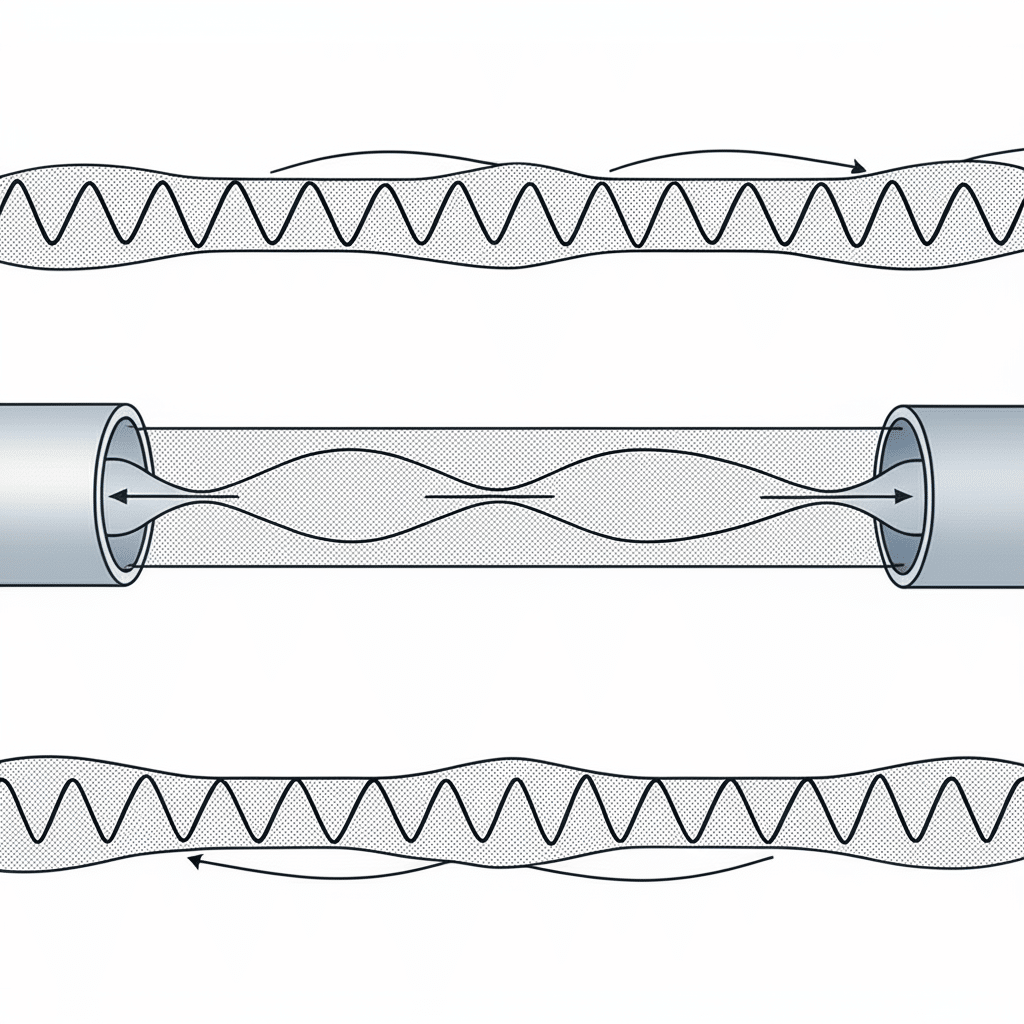
Tijdens een recent project bij een fabrikant van medische apparatuur in Massachusetts vertoonde hun pneumatische precisiepositioneersysteem mysterieuze krachtfluctuaties bij specifieke werkfrequenties. Door verificatietests met staande golven uit te voeren, stelden we vast dat hun toevoerleiding van 2,1 meter een fundamentele resonantie had bij 81 Hz, die precies overeenkwam met de cyclische frequentie van hun actuator. Deze resonantie versterkte drukschommelingen met 320%. Door de leidinglengte aan te passen naar 1,8 meter, verschoven we de resonantiefrequentie weg van hun werkbereik en werd het probleem volledig geëlimineerd, waardoor de positioneringsnauwkeurigheid verbeterde van ±0,8 mm naar ±0,15 mm.
Grondbeginselen van staande golven
Staande golven worden gevormd wanneer invallende en gereflecteerde golven interfereren, waardoor vaste patronen van drukknopen (minimale fluctuatie) en antinopen (maximale fluctuatie) ontstaan.
De resonantiefrequenties voor een pneumatische leiding hangen af van de randvoorwaarden:
Voor een leiding met gesloten uiteinden (meestal voorkomend in pneumatische systemen):
f = nc/2L
Waar:
- f = resonantiefrequentie (Hz)
- n = harmonisch getal (1, 2, 3, enz.)
- c = golfsnelheid (m/s)
- L = Lijnlengte (m)
Voor een lijn met één open uiteinde:
f = (2n-1)c/4L
Voor een leiding waarvan beide uiteinden open zijn (zeldzaam in pneumatiek):
f = nc/2L
Experimentele verificatiemethoden
Verschillende technieken kunnen patronen van staande golven in pneumatische systemen verifiëren:
Meerdere druksensoren
- Installeer drukopnemers op regelmatige afstanden langs de pneumatische leiding
- Stimuleer het systeem met een frequentiegolf of impuls
- Registreer drukschommelingen op elke locatie
- Breng de drukamplitude vs. positie in kaart om knooppunten en antinodes te identificeren
- Gemeten frequenties vergelijken met theoretische voorspellingen
Akoestische correlatie
- Akoestische sensoren (microfoons) gebruiken om geluid te detecteren via drukschommelingen
- De geluidsintensiteit correleren met de bedrijfsfrequentie
- Pieken in geluidsintensiteit identificeren die overeenkomen met resonantiefrequenties
- Controleer of pieken optreden bij de voorspelde frequenties
Versnellingsmeters
- Bevestig versnellingsmeters op pneumatische leidingen en componenten
- Meet de trillingsamplitude over het hele frequentiebereik
- Resonante pieken in het trillingsspectrum identificeren
- Correleren met voorspelde staande golffrequenties
Praktische berekening van de frequentie van staande golven
Voor een typisch pneumatisch systeem met:
- Lijnlengte (L): 3 meter
- Golfsnelheid (c): 343 m/s
- Configuratie met gesloten uiteinden
De fundamentele resonantiefrequentie zou zijn:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
En de harmonischen zouden dat zijn:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Deze frequenties vertegenwoordigen potentiële probleempunten waar drukschommelingen kunnen worden versterkt.
Staande-golfpatronen en hun effecten
| Harmonisch | Knooppunt-/antinodepatroon | Systeemeffecten | Kritieke onderdelen beïnvloed |
|---|---|---|---|
| Fundamenteel (n=1) | Eén drukknoop in het midden | Grote drukverschillen middellijn | In-line componenten, fittingen |
| Tweede (n=2) | Twee antinodes, knoop in het midden | Drukvariaties bij uiteinden | Kleppen, actuators, regelaars |
| Derde (n=3) | Drie antinodes, twee knooppunten | Complex drukpatroon | Meerdere systeemcomponenten |
| Vierde (n=4) | Vier antinodes, drie knooppunten | Hoogfrequente oscillaties | Afdichtingen, kleine onderdelen |
Casestudie experimentele verificatie
Voor een pneumatisch precisiepositioneringssysteem dat inconsistente prestaties levert:
| Parameter | Theoretische voorspelling | Experimentele meting | Correlatie |
|---|---|---|---|
| Fundamentele frequentie | 81,2 Hz | 79,8 Hz | 98.3% |
| Tweede harmonische | 162,4 Hz | 160,5 Hz | 98.8% |
| Derde harmonische | 243,6 Hz | 240,1 Hz | 98.6% |
| Drukversterking | 3:1 bij resonantie (geschat) | 3,2:1 bij resonantie (gemeten) | 93.8% |
| Locaties van knooppunten | 0, 1,05, 2,1 meter | 0, 1,08, 2,1 meter | 97.2% |
Deze casestudie toont de uitstekende overeenkomst aan tussen theoretische voorspellingen en experimentele metingen van staande-golfverschijnselen.
Praktische implicaties van staande golven
Staande golven veroorzaken een aantal belangrijke problemen in pneumatische systemen:
Drukversterking
- Fluctuaties kunnen 3-5× versterkt worden bij resonantie
- Kan de drukwaarden van componenten overschrijden
- Creëert krachtvariaties in actuatorenVermoeidheid van onderdelen
- Hoogfrequente drukwisselingen versnellen slijtage van afdichtingen
- Trillingen veroorzaken losraken van de fitting en lekkage
- Verkort de levensduur van het systeem met 30-70% in ernstige gevallenControle Instabiliteit
- Teruggekoppelde systemen kunnen oscilleren bij resonantiefrequenties
- Positie- en krachtregeling wordt onvoorspelbaar
- Kan zelfversterkende oscillaties creërenEnergieverliezen
- Staande golven vertegenwoordigen opgesloten energie
- Kan het energieverbruik verhogen met 10-30%
- Vermindert de algehele efficiëntie van het systeem
Pulsverzwakkingsmethoden: Welke technieken dempen effectief destructieve drukschommelingen?
Het beheersen van drukschommelingen is essentieel voor een betrouwbare werking van een pneumatisch systeem. Er kunnen verschillende dempingsmethoden worden toegepast om problematische drukschommelingen te verminderen of te elimineren.
Drukpulsdemping in pneumatische systemen kan op verschillende manieren worden bereikt: volumekamers die energie absorberen door gascompressie, beperkende elementen die demping creëren door viskeuze effecten, afgestemde resonatoren die specifieke frequenties annuleren en actieve annuleringssystemen die tegenpulsen genereren. Voor effectieve demping moet de methode worden afgestemd op de specifieke frequentie-inhoud en amplitude van de drukschommelingen.
Ik heb onlangs gewerkt met een fabrikant van verpakkingsmachines in Illinois, wiens snelle pneumatische systeem last had van ernstige drukschommelingen die inconsistente afdichtingskrachten veroorzaakten. Hun ingenieurs hadden zonder succes eenvoudige opvangtanks geprobeerd. Door een gedetailleerde analyse van de drukpulsen ontdekten we dat hun systeem meerdere frequentiecomponenten had die verschillende dempingsmethoden vereisten. Door een hybride oplossing te implementeren die een Helmholtz resonator5 afgestemd op hun dominante 112 Hz oscillatie en een reeks restrictie-openingen, verminderden we de drukschommelingen met 94% en elimineerden we de inconsistenties in de afdichting volledig.
Fundamentele dempingsmechanismen
Er kunnen verschillende fysische mechanismen worden gebruikt om drukpulsen te dempen:
Volume-gebaseerde verzwakking
Werkt door samendrukbaarheid van gas:
- Biedt een nalevingselement dat drukenergie absorbeert
- Het meest effectief voor fluctuaties met een lage frequentie
- Eenvoudige implementatie met minimale drukval
Verzwakking op basis van restricties
Werkt door viskeuze dissipatie:
- Zet drukenergie om in warmte door wrijving
- Effectief over een breed frequentiebereik
- Creëert permanente drukval
Resonator-gebaseerde demping
Werkt door middel van afgestemde destructieve interferentie:
- Annuleert specifieke frequentiecomponenten
- Zeer effectief voor gerichte frequenties
- Minimale invloed op doorstroming in stationaire toestand
Materiaal-gebaseerde demping
Werkt door flexibiliteit en demping van de muur:
- Absorbeert energie door wandvervorming
- Biedt breedbanddemping
- Kan worden geïntegreerd in bestaande componenten
Ontwerpprincipes volumekamer
Volumekamers (opvangtanks) zijn de meest voorkomende dempingsapparaten:
De effectiviteit van een volumekamer hangt af van de verhouding tussen het kamervolume en het lijnvolume:
Verzwakkingsverhouding = 1 + (Vc/Vl)
Waar:
- Vc = kamervolume
- Vl = Lijnvolume
Voor frequentie-afhankelijke analyse is de transmissieverhouding:
TR = 1/√(1 + (ωVc/Zc)²)
Waar:
- ω = hoekfrequentie (2πf)
- Zc = karakteristieke impedantie van de lijn
Beperkende element verzwakking
Openingen, poreuze materialen en lange smalle doorgangen creëren demping door viskeuze effecten:
De drukval over een restrictie is als volgt:
ΔP = k(ρv²/2)
Waar:
- k = verliescoëfficiënt
- ρ = gasdichtheid
- v = Snelheid
De demping neemt toe met:
- Hogere stroomsnelheid
- Grotere beperkingslengte
- Kleinere doorlaatdiameter
- Kronkeliger stromingstraject
Resonator dempingssystemen
Afgestemde resonatoren zorgen voor een gerichte frequentiedemping:
Helmholtz Resonator
Een volumekamer met een smalle hals, afgestemd op een specifieke frequentie:
f = (c/2π)√(A/VL)
Waar:
- f = resonantiefrequentie
- c = geluidssnelheid
- A = dwarsdoorsnede van de hals
- V = kamervolume
- L = effectieve halslengte
Kwartgolfresonator
Een buis met een bepaalde lengte die aan één uiteinde open is:
f = c/4L
Waar:
- L = buislengte
Resonatoren met zijwanden
Meerdere afgestemde takken voor complexe frequentie-inhoud:
- Elke tak richt zich op een specifieke frequentie
- Kan meerdere harmonischen tegelijk aanpakken
- Minimale impact op hoofdstroompad
Actieve annuleringssystemen
Geavanceerde systemen die tegenpulsen genereren:
Detectiefase
- Inkomende drukgolven detecteren
- Analyseer frequentie-inhoud en amplitudeVerwerkingsfase
- Bereken het vereiste annuleringssignaal
- Rekening houden met systeemdynamiek en vertragingenBedieningsfase
- Genereer tegendrukgolven
- Precies op tijd voor destructieve interferentie
Vergelijking van dempingsprestaties
| Methode | Lage frequentie (<50 Hz) | Middenfrequentie (50-200 Hz) | Hoge frequentie (>200 Hz) | Drukval | Complexiteit |
|---|---|---|---|---|---|
| Volumekamer | Uitstekend (>90%) | Matig (40-70%) | Slecht (<30%) | Zeer laag | Laag |
| Restrictieve opening | Slecht (<30%) | Goed (60-80%) | Uitstekend (>80%) | Hoog | Laag |
| Helmholtz Resonator | Slechte resonantie van buiten | Uitstekend in resonantie | Slechte resonantie van buiten | Laag | Medium |
| Kwartgolfbuis | Slechte resonantie van buiten | Uitstekend in resonantie | Slechte resonantie van buiten | Laag | Medium |
| Meerdere resonatoren | Matig (40-60%) | Uitstekend (>80%) | Goed (60-80%) | Laag | Hoog |
| Actieve annulering | Uitstekend (>90%) | Uitstekend (>90%) | Goed (70-85%) | Geen | Zeer hoog |
| Hybride systemen | Uitstekend (>90%) | Uitstekend (>90%) | Uitstekend (>90%) | Matig | Hoog |
Praktische implementatie van demping
Voor effectieve demping van drukpulsen:
De schommelingen karakteriseren
- Meet de amplitude en frequentie-inhoud
- Identificeer dominante frequenties
- Bepaal of breedband of specifieke frequenties verzwakt moeten wordenGeschikte methoden selecteren
- Voor lage frequenties: Volumekamers
- Voor specifieke frequenties: Afgestemde resonatoren
- Voor breedbanddemping: Beperkingen of hybride benaderingen
- Voor kritieke toepassingen: Actieve annuleringPlaatsing optimaliseren
- In de buurt van bronnen om verspreiding te voorkomen
- In de buurt van gevoelige componenten om ze te beschermen
- Op strategische locaties om staande golfpatronen te doorbrekenPrestaties controleren
- Meet voor/na verzwakking
- Bevestig alle bedrijfsomstandigheden
- Geen onbedoelde gevolgen
Casestudie: Multi-methode demping in snelle verpakkingen
Voor een pneumatisch afdichtingssysteem met hoge snelheid dat drukschommelingen ondervindt:
| Parameter | Vóór verzwakking | Na volumekamer | Na de hybride oplossing | Verbetering |
|---|---|---|---|---|
| Lage frequentie (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | 94% reductie |
| Middenfrequentie (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | 94% reductie |
| Hoge frequentie (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | 90% vermindering |
| Variatie in afdichtingskracht | ±28% | ±22% | ±2,5% | 91% verbetering |
| Afgekeurd product | 4.2% | 3.1% | 0.3% | 93% vermindering |
| Systeemefficiëntie | Basislijn | +4% | +12% | 12% verbetering |
Deze casestudie laat zien hoe een gerichte, multi-methodische benadering van demping de systeemprestaties drastisch kan verbeteren.
Geavanceerde dempingstechnieken
Voor bijzonder uitdagende toepassingen:
Gedistribueerde verzwakking
Meerdere kleinere apparaten gebruiken in plaats van één groot apparaat:
- Plaatst demping dichter bij zowel bronnen als gevoelige componenten
- Breekt staande golfpatronen effectiever
- Biedt redundantie en consistentere prestaties
Frequentieselectieve demping
Gericht op specifieke probleemfrequenties:
- Gebruikt meerdere resonatoren afgestemd op verschillende frequenties
- Behoudt de gewenste systeemrespons terwijl problemen worden geëlimineerd
- Minimaliseert de impact op de algehele systeemprestaties
Adaptieve systemen
De demping aanpassen op basis van de bedrijfsomstandigheden:
- Gebruikt sensoren om drukschommelingen te controleren
- Past dempingsparameters automatisch aan
- Optimaliseert de prestaties onder verschillende omstandigheden
Conclusie
Inzicht in de drukschommelingstheorie-golfvoortplantingssnelheid, verificatie van staande golven en pulsverzwakkingsmethoden vormt de basis voor een betrouwbaar en efficiënt ontwerp van pneumatische systemen. Door deze principes toe te passen, kunt u mysterieuze prestatieproblemen elimineren, de levensduur van componenten verlengen en de systeemefficiëntie verbeteren terwijl een consistente werking onder alle bedrijfsomstandigheden wordt gegarandeerd.
Veelgestelde vragen over drukschommelingen in pneumatische systemen
Hoe beïnvloeden drukschommelingen de levensduur van pneumatische onderdelen?
Drukschommelingen verminderen de levensduur van componenten aanzienlijk via verschillende mechanismen: ze veroorzaken versnelde slijtage van afdichtingen door microbewegingen te creëren op afdichtingsoppervlakken; ze veroorzaken materiaalmoeheid in membranen en flexibele elementen door herhaalde spanningscycli; ze bevorderen het loskomen van schroefverbindingen door trillingen; en ze creëren plaatselijke spanningsconcentraties op geometrische overgangen. Systemen met ernstige ongecontroleerde drukschommelingen hebben meestal een 40-70% kortere levensduur van onderdelen in vergelijking met goed gedempte systemen, waarbij vooral afdichtingen en membranen kwetsbaar zijn.
Wat is de relatie tussen leidinglengte en drukreactietijd in pneumatische systemen?
De lengte van de leiding is rechtstreeks van invloed op de drukresponsietijd volgens een eenvoudige relatie: de responsietijd neemt lineair toe met de lengte van de leiding, met een snelheid die wordt bepaald door de voortplantingssnelheid van de golf. Voor lucht onder standaardomstandigheden (golfsnelheid ≈ 343 m/s) voegt elke meter leiding ongeveer 2,9 milliseconden transmissievertraging toe. De werkelijke drukopbouwtijd is echter meestal 2-5 keer langer dan de initiële golftransmissietijd omdat er meerdere reflecties nodig zijn om de druk gelijk te maken. Dit betekent dat een lijn van 5 meter een golftransmissietijd van 14,5 ms kan hebben, maar een drukopbouwtijd van 30-70 ms.
Hoe kan ik vaststellen of mijn pneumatisch systeem last heeft van resonante drukschommelingen?
Resonante drukschommelingen manifesteren zich meestal via verschillende waarneembare symptomen: componenten trillen bij specifieke werkingsfrequenties maar niet bij andere; de systeemprestaties variëren inconsistent bij kleine veranderingen in de werkingsomstandigheden; er is hoorbaar "gezang" of "gefluit" uit pneumatische leidingen; drukmeters vertonen oscillerende waarden; en de actuatorprestaties (snelheid, kracht) variëren cyclisch. Om resonantie te bevestigen, meet u de druk op verschillende punten in het systeem met snel reagerende transducers (reactietijd < 1 ms) en zoekt u naar staande golfpatronen waarbij de drukamplitude varieert met de positie langs de leiding.
Hebben drukschommelingen invloed op de energie-efficiëntie in pneumatische systemen?
Drukschommelingen hebben een aanzienlijke invloed op de energie-efficiëntie en verminderen deze meestal met 10-25% via verschillende mechanismen: ze verhogen de lekkage door hogere piekdrukken te creëren; ze verspillen energie door cyclische compressie en expansie; ze veroorzaken verhoogde wrijving in componenten door trillingen; en ze leiden er vaak toe dat operators de toevoerdruk verhogen om prestatieproblemen te compenseren. Bovendien zetten de turbulentie en stromingsscheiding die door drukschommelingen worden veroorzaakt, nuttige drukenergie om in afvalwarmte. Het op de juiste manier dempen van drukschommelingen kan de systeemefficiëntie met 5-15% verbeteren zonder andere veranderingen.
Hoe beïnvloeden temperatuurveranderingen het gedrag van drukgolven in pneumatische systemen?
Temperatuur heeft een aanzienlijke invloed op het gedrag van drukgolven via verschillende mechanismen: het beïnvloedt direct de voortplantingssnelheid van de golven (ongeveer +0,6 m/s per °C toename); het verandert de gasdichtheid en viscositeit, waardoor de dempingskarakteristieken veranderen; het wijzigt de elastische eigenschappen van pneumatische leidingen, waardoor de weerkaatsing en transmissie van de golven worden beïnvloed; en het verschuift de resonantiefrequenties (ongeveer +0,17% per °C). Deze temperatuurgevoeligheid betekent dat een systeem dat perfect werkt bij 20°C problematische resonanties kan ondervinden bij 40°C, of dat dempingsapparaten die zijn afgestemd op winterse omstandigheden in de zomer ineffectief kunnen zijn.
-
Geeft een gedetailleerde uitleg over de natuurkunde achter de geluidssnelheid, hoe deze wordt berekend en de factoren die de snelheid beïnvloeden. ↩
-
Biedt een fundamenteel begrip van staande golffenomenen, inclusief hoe ze ontstaan uit interferentie en hun belangrijkste kenmerken zoals knooppunten en antinodes. ↩
-
Biedt bewijs en industriële studies die het typische bereik van energieverliezen verifiëren die worden veroorzaakt door inefficiënties zoals drukschommelingen in pneumatische systemen. ↩
-
Legt de onderdelen en functie uit van een luchtvoorbereidingsunit (FRL), die essentieel is voor het handhaven van de luchtkwaliteit in pneumatische systemen. ↩
-
Biedt een diepgaande uitleg van de principes achter een Helmholtz-resonator, een essentieel apparaat voor gerichte frequentiedemping in akoestische en vloeistofsystemen. ↩



