Are you struggling with slow cylinder speeds, inconsistent motion, or insufficient force in your pneumatic systems? These common problems often stem from a misunderstood culprit: flow resistance. Many engineers size their pneumatic components based solely on pressure and force requirements, overlooking the critical impact of flow resistance on real-world performance.
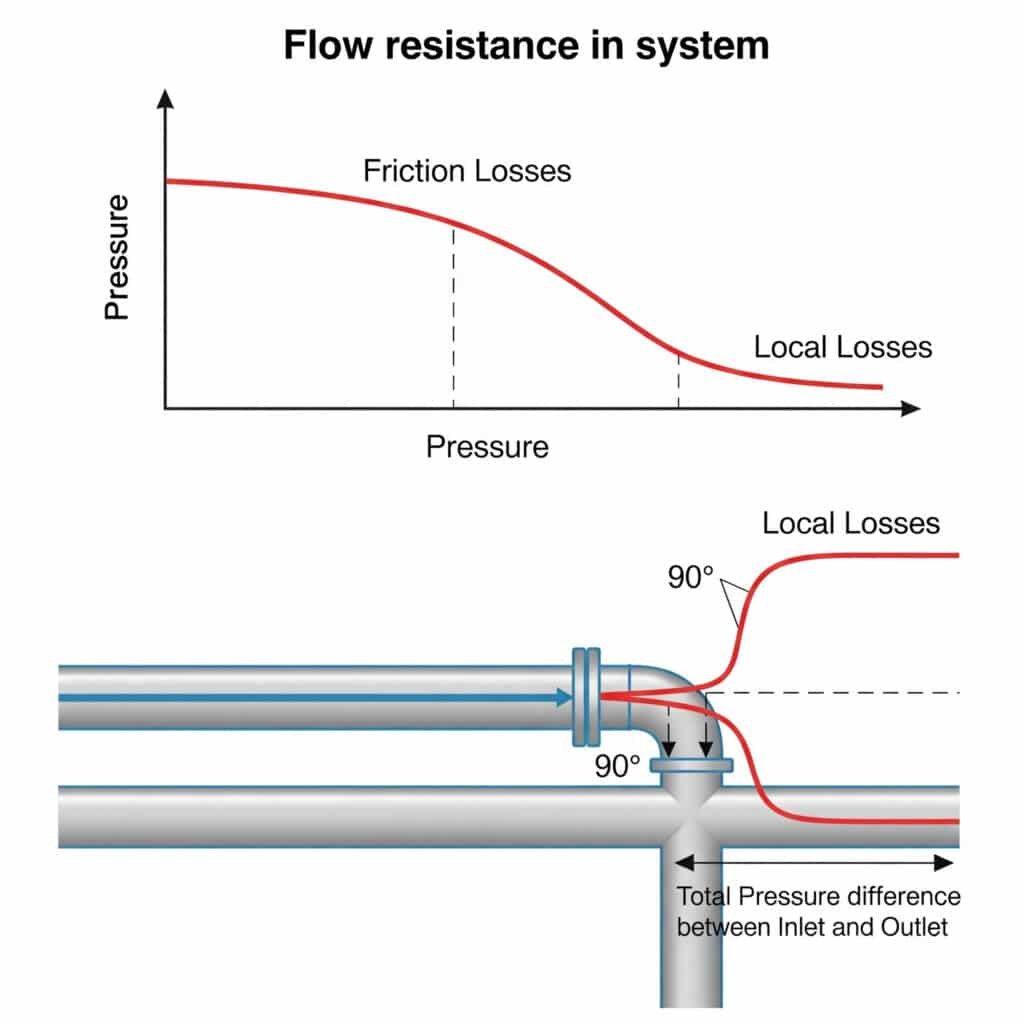
Flow resistance in pneumatic systems creates pressure drops that reduce available force, limit maximum speed, and cause inconsistent motion. This resistance comes from both friction along straight pipes (friction losses) and disruptions at fittings, bends, and valves (local losses). Together, these resistances can reduce actual system performance by 20-50% compared to theoretical calculations.
In my 15+ years at Bepto working with pneumatic systems, I’ve seen countless cases where understanding and addressing flow resistance has transformed underperforming systems into reliable, efficient operations. Let me share what I’ve learned about calculating and minimizing these hidden performance killers.
Table of Contents
- How Do You Actually Calculate Friction Losses in Pneumatic Lines?
- Why Is the Equivalent Length Method Critical for Accurate System Design?
- What Happens When Air Flows Through Reduced Bore Sections?
- Conclusion
- FAQs About Flow Resistance in Pneumatic Systems
How Do You Actually Calculate Friction Losses in Pneumatic Lines?
Friction losses in straight pipes and tubes are the foundation of flow resistance calculations, but many engineers rely on oversimplified rules of thumb that lead to undersized systems.
Friction losses in pneumatic lines are calculated using the Darcy-Weisbach equation1: ΔP = λ(L/D)(ρv²/2), where λ is the friction factor, L is pipe length, D is pipe diameter, ρ is air density, and v is flow velocity. For pneumatic systems, the friction factor λ varies based on Reynolds number2 and relative roughness, and is typically determined using lookup tables or the Moody diagram3.
Understanding friction losses has practical implications for system design and troubleshooting. Let me break this down into actionable insights.
Using Friction Factor Tables Effectively
The friction factor (λ) is the key parameter in calculating pressure drops, but determining its value requires consideration of flow conditions:
| Flow Regime | Reynolds Number (Re) | Friction Factor Determination |
|---|---|---|
| Laminar Flow | Re < 2000 | λ = 64/Re |
| Transitional Flow | 2000 < Re < 4000 | Unreliable – avoid designing in this range |
| Turbulent Flow | Re > 4000 | Use lookup tables based on relative roughness (ε/D) |
Practical Friction Factor Lookup Table
For turbulent flow in pneumatic systems, use this simplified table:
| Pipe Material | Relative Roughness (ε/D) | Friction Factor (λ) at Common Reynolds Numbers |
|---|---|---|
| Re = 10,000 | ||
| Smooth Tubing (PVC, Polyurethane) | 0.0001 – 0.0005 | 0.031 |
| Aluminum Tubing | 0.001 – 0.002 | 0.035 |
| Galvanized Steel | 0.003 – 0.005 | 0.042 |
| Rusted Steel | 0.01 – 0.05 | 0.054 |
Calculating Pressure Drop in Real Pneumatic Systems
Let’s walk through a practical example:
| Parameter | Value/Calculation | Example |
|---|---|---|
| Pipe Diameter (D) | Internal diameter | 8mm (0.008m) |
| Pipe Length (L) | Total straight length | 5m |
| Flow Rate (Q) | From system requirements | 20 standard liters/second |
| Air Density (ρ) | At operating pressure | 7.2 kg/m³ at 6 bar |
| Flow Velocity (v) | v = Q/(π×D²/4) | v = 0.02m³/s/(π×0.008²/4) = 398 m/s |
| Reynolds Number (Re) | Re = ρvD/μ | Re = 7.2×398×0.008/1.8×10⁻⁵ = 1,273,600 |
| Relative Roughness | For polyurethane tubing | 0.0003 |
| Friction Factor (λ) | From lookup table | 0.017 |
| Pressure Drop (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0.017×(5/0.008)×(7.2×398²/2) = 6.07 bar |
Real-World Application: Solving Cylinder Speed Issues
Last year, I worked with Sarah, a manufacturing engineer at a packaging equipment company in Wisconsin. Her rodless cylinder system was operating at only 60% of the expected speed, despite having the correctly sized cylinder and adequate supply pressure.
After analyzing her system, I discovered that she was using 6mm tubing for a high-flow application. The friction losses were causing a 2.1 bar pressure drop, significantly reducing the available force and speed. By upgrading to 10mm tubing, we reduced the pressure drop to 0.4 bar, and her system immediately achieved the required performance without any other changes.
Factors Affecting Friction Losses in Real Systems
Several factors influence actual friction losses:
- Air temperature: Higher temperatures increase viscosity and friction
- Contamination: Dirt and oil can increase effective roughness
- Tube bending: Micro-deformation in bent tubes increases resistance
- Age deterioration: Corrosion and deposits increase roughness over time
- Operating pressure: Higher pressures increase density and losses
Why Is the Equivalent Length Method Critical for Accurate System Design?
Local losses at fittings, valves, and bends often exceed friction losses in straight pipes, yet many engineers either ignore them or use crude estimation methods that lead to performance problems.
The equivalent length method converts local losses from fittings and valves into an equivalent length of straight pipe that would cause the same pressure drop. This is calculated using Le = K(D/λ), where Le is the equivalent length, K is the local loss coefficient4, D is the pipe diameter, and λ is the friction factor. This method simplifies calculations and provides more accurate system performance predictions.
Let’s explore how to apply this method effectively in pneumatic system design.
Equivalent Length Tables for Common Pneumatic Components
Here’s a practical reference table for common pneumatic components:
| Component | K-Value | Equivalent Length (Le/D) |
|---|---|---|
| 90° Elbow (sharp) | 0.9 | 30 |
| 90° Elbow (standard radius) | 0.3 | 10 |
| 45° Elbow | 0.2 | 7 |
| T-Junction (through flow) | 0.3 | 10 |
| T-Junction (branch flow) | 1.0 | 33 |
| Ball Valve (fully open) | 0.1 | 3 |
| Gate Valve (fully open) | 0.2 | 7 |
| Quick Connect Coupling | 0.4-0.8 | 13-27 |
| Check Valve | 1.5-2.5 | 50-83 |
| Standard Flow Control Valve | 1.0-3.0 | 33-100 |
Applying the Equivalent Length Method
To use this method effectively:
- Identify all components in your pneumatic circuit
- Find the K-value or equivalent length ratio (Le/D) for each component
- Calculate the equivalent length by multiplying by the pipe diameter
- Add all equivalent lengths to the actual straight pipe length
- Use the total effective length in your friction loss calculations
For example, a system with 5m of straight 8mm tubing plus four 90° elbows, one T-junction, and two quick connects:
| Component | Quantity | Le/D | Equivalent Length |
|---|---|---|---|
| 90° Elbows | 4 | 10 | 4 × 10 × 0.008m = 0.32m |
| T-Junction | 1 | 10 | 1 × 10 × 0.008m = 0.08m |
| Quick Connects | 2 | 20 | 2 × 20 × 0.008m = 0.32m |
| Total Equivalent Length | 0.72m | ||
| Actual Straight Length | 5.00m | ||
| Total Effective Length | 5.72m |
This means your 5m system actually behaves like a 5.72m system due to local losses—a 14.4% increase in effective length.
Case Study: Optimizing Valve Placement in Assembly Systems
I recently helped Miguel, an automation engineer at an electronics assembly plant in Arizona. His pick-and-place system was experiencing inconsistent motion and cycle time variations, despite using high-quality components.
Analysis revealed that his valve manifold was located 3m away from the cylinders, and the circuit included numerous fittings. The equivalent length calculation showed that his 3m actual distance had an effective length of 7.2m due to local losses—more than double the straight-pipe distance!
By relocating the valve manifold closer to the cylinders and eliminating several fittings, we reduced the effective length from 7.2m to 2.1m. This decreased the pressure drop by 70%, resulting in consistent motion and a 15% reduction in cycle time.
Practical Tips for Minimizing Local Losses
To reduce local losses in your pneumatic systems:
- Use swept or rounded elbows instead of sharp bends (reduces K-value by 67%)
- Minimize the number of fittings by planning more direct routing
- Select low-restriction components like full-bore ball valves where appropriate
- Size fittings properly – undersized fittings cause disproportionate losses
- Place valves close to actuators to minimize effective tubing length
What Happens When Air Flows Through Reduced Bore Sections?
Reduced bore sections in pneumatic circuits—such as partially closed valves, undersized fittings, or diameter transitions—create significant flow restrictions that can severely impact system performance.
When air flows through reduced bore sections, pressure drops5 occur according to the formula ΔP = ρ(v₂² – v₁²)/2, where v₁ is velocity before the restriction and v₂ is velocity in the restriction. This can be compensated for using the bore ratio compensation factor C = (1 – (d/D)⁴), where d is the reduced diameter and D is the original diameter. This factor helps predict actual system performance and avoid undersizing components.
Let’s explore the practical implications of reduced bore sections and how to account for them in system design.
Calculating Pressure Drops at Diameter Transitions
When air flows from a larger diameter to a smaller one, the pressure drop can be calculated using:
| Parameter | Formula | Example |
|---|---|---|
| Original Diameter (D) | From specifications | 10mm |
| Reduced Diameter (d) | From specifications | 6mm |
| Bore Ratio (d/D) | Simple division | 0.6 |
| Flow Rate (Q) | From system requirements | 15 standard liters/second |
| Velocity in Original Pipe (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Velocity in Reduced Section (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Pressure Drop (ΔP) | ΔP = ρ(v₂² – v₁²)/2 | 0.88 bar |
| Compensation Factor (C) | C = (1 – (d/D)⁴) | 0.87 |
Common Bore Reduction Scenarios and Their Impact
Here’s how different bore reductions affect flow capacity:
| Bore Reduction | Flow Capacity Reduction | Pressure Drop Increase |
|---|---|---|
| 10mm to 8mm | 36% | 2.4× |
| 10mm to 6mm | 64% | 7.7× |
| 10mm to 4mm | 84% | 39× |
| 8mm to 6mm | 44% | 3.2× |
| 8mm to 4mm | 75% | 16× |
| 6mm to 4mm | 56% | 5.1× |
These numbers highlight why seemingly minor reductions in diameter can have dramatic effects on system performance.
The Cumulative Effect of Multiple Restrictions
In real pneumatic circuits, multiple restrictions occur in series. Their effect is cumulative and can be calculated using:
- Convert each restriction to its equivalent C-factor
- Calculate the total C-factor: Ctotal = 1 – (1-C₁)(1-C₂)(1-C₃)…
- Use this total factor to determine the overall system performance reduction
Case Study: Solving Valve-Actuator Mismatch Issues
Last month, I worked with Thomas, a maintenance supervisor at a furniture manufacturing plant in North Carolina. His new rodless cylinder system was operating at less than half the expected speed, despite using the manufacturer’s recommended valve size.
Investigation revealed multiple bore reductions in his circuit:
- 10mm supply line to 8mm valve ports (C₁ = 0.36)
- 8mm valve ports to 6mm fittings (C₂ = 0.44)
- 6mm fittings to 8mm cylinder ports with internal restrictions (C₃ = 0.32)
The total compensation factor was Ctotal = 1 – (1-0.36)(1-0.44)(1-0.32) = 0.75, meaning his system was losing 75% of its theoretical flow capacity!
By upgrading to properly sized components throughout the system, we eliminated these restrictions and achieved the required performance without changing the cylinder or supply pressure.
Practical Strategies to Minimize Bore Reduction Losses
To reduce losses from bore reductions:
- Size components consistently throughout the pneumatic circuit
- Use the largest practical tubing size for high-flow applications
- Pay attention to internal component restrictions, not just connection sizes
- Consider parallel flow paths for high-flow requirements
- Eliminate unnecessary adapters and transitions wherever possible
The “Weakest Link” Principle in Pneumatic Systems
Remember that your pneumatic system’s performance is limited by its most restrictive component. A single undersized element can negate the benefits of properly sized components elsewhere in the system.
For example, a system with 10mm tubing, 10mm valves, but 6mm fittings at the cylinder will perform essentially the same as a system with 6mm components throughout—at a higher cost.
Conclusion
Understanding and properly calculating flow resistance—through friction factor tables, equivalent length methods, and reduced bore compensation—is essential for designing pneumatic systems that perform as expected in real-world conditions. By applying these calculation methods and design principles, you can optimize your rodless cylinder applications and other pneumatic systems for maximum performance and reliability.
FAQs About Flow Resistance in Pneumatic Systems
How much pressure drop is acceptable in a pneumatic system?
The acceptable pressure drop depends on your application requirements, but as a general guideline, limit total pressure drop to 10-15% of supply pressure for efficient operation. For a 6 bar system, this means keeping total pressure drop under 0.6-0.9 bar. Critical applications may require even lower pressure drops of 5-8% to maintain consistent performance.
What’s the relationship between tube diameter and pressure drop?
Pressure drop is inversely proportional to the fifth power of the diameter (D⁵) for turbulent flow in pneumatic systems. This means doubling the tube diameter reduces pressure drop by approximately 32 times. For example, increasing from 6mm to 12mm tubing can reduce pressure drop from 1.5 bar to just 0.047 bar under the same flow conditions.
How do I determine the right tube size for my pneumatic application?
Select tube size based on flow rate requirements and acceptable pressure drop. Calculate the Reynolds number and friction factor, then use the Darcy-Weisbach equation to determine pressure drop for different diameters. Choose the smallest diameter that keeps pressure drop within acceptable limits (typically <10% of supply pressure) while considering space constraints and cost.
What creates more restriction: a 90° elbow or 5 meters of straight tubing?
A sharp 90° elbow typically creates resistance equivalent to 30 pipe diameters of straight tubing. For 8mm tubing, one sharp elbow equals approximately 240mm (30 × 8mm) of straight tubing. This means that 5 meters of straight tubing creates about 21 times more restriction than a single elbow. However, systems often contain multiple elbows and fittings, whose cumulative effect can exceed straight-length losses.
How do quick-connect fittings affect system performance?
Standard quick-connect fittings typically introduce a local loss equivalent to 15-25 pipe diameters of straight tubing. More significantly, many quick-connects have internal restrictions smaller than their nominal size. A “10mm” quick-connect might have an internal restriction of only 7-8mm, creating a bore reduction that can reduce flow capacity by 50-70% at that point.
What’s the impact of partially closed flow control valves on system performance?
A flow control valve closed to 50% of its full bore area doesn’t reduce flow by just 50%—it reduces flow by approximately 75% due to the non-linear relationship between diameter and flow capacity. The pressure drop increases according to the square of velocity change, so halving the effective diameter increases pressure drop by approximately 16 times under the same flow conditions.
-
Provides a detailed breakdown of the Darcy-Weisbach equation, a fundamental and widely used formula in fluid dynamics for calculating pressure loss due to friction in a pipe. ↩
-
Offers a clear definition of the Reynolds number, a critical dimensionless quantity used to predict flow patterns (laminar or turbulent) in different fluid flow situations. ↩
-
Presents the Moody diagram, a comprehensive graph that plots the Darcy friction factor against the Reynolds number and relative roughness, which is the standard tool for engineers to determine pressure drop in pipes. ↩
-
Explains the concept of the K-value, or local loss coefficient, a dimensionless number used to characterize the pressure loss in a pipe fitting or valve as part of the equivalent length method. ↩
-
Details the physics behind the pressure drop that occurs when a fluid passes through a restriction (an orifice), based on the principles of the continuity equation and Bernoulli’s principle. ↩




