
Avez-vous déjà touché un cylindre pneumatique Après avoir fonctionné en continu, vous avez été surpris par la chaleur ressentie ? Cette chaleur n'est pas seulement un désagrément - elle représente un gaspillage d'énergie, une réduction de l'efficacité et des problèmes de fiabilité potentiels qui pourraient coûter des milliers d'euros à votre entreprise.
Le transfert de chaleur dans les systèmes pneumatiques s'effectue par le biais de trois mécanismes : la conduction à travers les matériaux des composants, la convection entre les surfaces et l'air, et le rayonnement des surfaces chaudes. La compréhension et l'optimisation de ces principes peuvent réduire les températures de fonctionnement de 15 à 30%, prolonger la durée de vie des composants jusqu'à 40% et améliorer l'efficacité énergétique de 5 à 15%.
Le mois dernier, j'ai conseillé une usine de transformation alimentaire en Géorgie dont les cylindres sans tige tombaient en panne tous les 3 à 4 mois en raison de problèmes thermiques. L'équipe de maintenance se contentait de remplacer les composants sans s'attaquer à la cause première. En appliquant les principes de transfert de chaleur appropriés, nous avons réduit les températures de fonctionnement de 22°C et prolongé la durée de vie des composants de plus d'un an. Laissez-moi vous montrer comment nous avons procédé et comment vous pouvez appliquer ces mêmes principes à vos systèmes.
Table des matières
- Calcul du coefficient de conduction : Comment la chaleur se déplace-t-elle à travers vos composants ?
- Méthodes d'amélioration de la convection : Quelles sont les techniques qui maximisent le transfert de chaleur air-surface ?
- Modèle d'efficacité du rayonnement : Quand le rayonnement thermique est-il important dans les systèmes pneumatiques ?
- Conclusion
- FAQ sur le transfert de chaleur dans les systèmes pneumatiques
Calcul du coefficient de conduction : Comment la chaleur se déplace-t-elle à travers vos composants ?
La conduction est le principal mécanisme de transfert de chaleur dans les composants pneumatiques solides. Il est essentiel de comprendre comment calculer et optimiser les coefficients de conduction pour gérer les températures du système.
Le coefficient de conduction thermique peut être calculé comme suit Loi de Fourier1q = -k(dT/dx), où q est le flux de chaleur (W/m²), k est la conductivité thermique (W/m-K) et dT/dx est le gradient de température. Pour les composants pneumatiques, la conduction efficace dépend de la sélection des matériaux, de la qualité de l'interface et des facteurs géométriques qui affectent la longueur du trajet de la chaleur et la surface de la section transversale.
Je me souviens avoir dépanné une chaîne de fabrication dans le Tennessee où les roulements des cylindres sans tige tombaient en panne prématurément. L'équipe de maintenance avait essayé plusieurs lubrifiants sans succès. Lorsque nous avons analysé les chemins de conduction, nous avons découvert un goulot d'étranglement thermique au niveau de l'interface palier-corps. En améliorant l'état de surface et en appliquant un composé thermoconducteur, nous avons augmenté le coefficient de conduction effectif de 340% et éliminé complètement les défaillances.
Equations fondamentales de la conduction
Décortiquons les principales équations permettant de calculer la conduction dans les composants pneumatiques :
Loi de Fourier pour la conduction de la chaleur
L'équation de base régissant la conduction de la chaleur est la suivante :
q = -k(dT/dx)
Où ?
- q = Flux de chaleur (W/m²)
- k = Conductivité thermique (W/m-K)
- dT/dx = Gradient de température (K/m)
Pour un cas unidimensionnel simple avec une section transversale constante :
Q = kA(T₁-T₂)/L
Où ?
- Q = Taux de transfert de chaleur (W)
- A = Surface de la section transversale (m²)
- T₁, T₂ = Températures à chaque extrémité (K)
- L = Longueur du chemin de chaleur (m)
Concept de résistance thermique
Pour les géométries complexes, l'approche de la résistance thermique est souvent plus pratique :
R = L/(kA)
Où ?
- R = Résistance thermique (K/W)
Pour les systèmes comportant plusieurs composants en série :
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Et le taux de transfert de chaleur devient :
Q = ΔT/Rtotal
Comparaison de la conductivité thermique des matériaux
| Matériau | Conductivité thermique (W/m-K) | Conductivité relative | Applications courantes |
|---|---|---|---|
| Aluminium | 205-250 | Haut | Cylindres, dissipateurs de chaleur |
| Acier | 36-54 | Moyen | Composants structurels |
| Acier inoxydable | 14-16 | Faible-Moyen | Environnements corrosifs |
| Bronze | 26-50 | Moyen | Roulements, bagues |
| PTFE | 0.25 | Très faible | Joints, roulements |
| Caoutchouc nitrile | 0.13 | Très faible | Joints toriques, joints d'étanchéité |
| Air (immobile) | 0.026 | Extremely Low | Gap filler |
| Thermal Paste | 3-8 | Faible | Interface material |
Contact Resistance in Pneumatic Assemblies
At interfaces between components, contact resistance significantly affects heat transfer:
Rcontact = 1/(hc × A)
Où ?
- hc = Contact coefficient (W/m²·K)
- A = Contact area (m²)
Factors affecting contact resistance include:
- Surface Roughness: Rougher surfaces have less actual contact area
- Contact Pressure: Higher pressure increases effective contact area
- Interface Materials: Thermal compounds fill air gaps
- Surface Cleanliness: Contaminants can increase resistance
Case Study: Rodless Cylinder Thermal Optimization
For a magnetic rodless cylinder experiencing thermal issues:
| Composant | Conception originale | Optimized Design | Amélioration |
|---|---|---|---|
| Cylinder Body | Anodized Aluminum | Same material, improved finish | 15% better conduction |
| Bearing Interface | Metal-to-metal contact | Added thermal compound | 340% better conduction |
| Supports de montage | Painted steel | Bare aluminum | 280% better conduction |
| Overall Thermal Resistance | 2.8 K/W | 0.7 K/W | 75% reduction |
| Température de fonctionnement | 78°C | 56°C | 22°C reduction |
| Component Life | 4 months | >12 months | 3× improvement |
Practical Conduction Optimization Techniques
Based on my experience with hundreds of pneumatic systems, here are the most effective approaches for improving conduction:
Interface Optimization
- Surface Finishing: Improve mating surface smoothness to Ra 0.4-0.8 μm
- Thermal Interface Materials2: Apply appropriate compounds (3-8 W/m·K)
- Fastener Torque: Ensure proper tightening for optimal contact pressure
- Cleanliness: Remove all oils and contaminants before assembly
Material Selection Strategies
- Critical Heat Paths: Use high-conductivity materials (aluminum, copper)
- Thermal Breaks: Intentionally use low-conductivity materials to isolate heat
- Composite Approaches: Combine materials for optimal performance/cost
- Anisotropic Materials: Utilize directional conductivity where appropriate
Geometric Optimization
- Heat Path Length: Minimize distance between heat sources and sinks
- Cross-Sectional Area: Maximize area perpendicular to heat flow
- Thermal Bottlenecks: Identify and eliminate constrictions in heat path
- Redundant Paths: Create multiple parallel conduction routes
Méthodes d'amélioration de la convection : Quelles sont les techniques qui maximisent le transfert de chaleur air-surface ?
Convection is often the limiting factor in pneumatic system cooling. Enhancing convective heat transfer can dramatically improve thermal management and system performance.
Convective heat transfer follows Newton’s Law of Cooling3: Q = hA(Ts-T∞), where h is the convection coefficient (W/m²·K), A is the surface area, and (Ts-T∞) is the temperature difference between the surface and fluid. Enhancement methods include increasing surface area through fins, improving fluid velocity with directed airflow, and optimizing surface characteristics to promote turbulent boundary layers.
During an energy efficiency audit at a packaging facility in Arizona, I encountered a pneumatic system operating in a 43°C ambient environment. Their rodless cylinders were overheating despite meeting all maintenance requirements. By implementing targeted convection enhancement—adding small aluminum fins and a low-power fan—we increased the convection coefficient by 450%. This reduced operating temperatures from dangerous levels to within specification without any major system modifications.
Convection Heat Transfer Fundamentals
The basic equation governing convective heat transfer is:
Q = hA(Ts-T∞)
Où ?
- Q = Taux de transfert de chaleur (W)
- h = Convection coefficient (W/m²·K)
- A = Surface area (m²)
- Ts = Surface temperature (K)
- T∞ = Fluid (air) temperature (K)
The convection coefficient h depends on multiple factors:
- Fluid properties (density, viscosity, thermal conductivity)
- Flow characteristics (velocity, turbulence)
- Surface geometry and orientation
- Flow regime (natural vs. forced convection)
Natural vs. Forced Convection
| Paramètres | Natural Convection | Forced Convection | Implications |
|---|---|---|---|
| Typical h Value | 5-25 W/m²·K | 25-250 W/m²·K | Forced convection can be 10× more effective |
| Driving Force | Buoyancy (temperature difference) | External pressure (fans, blowers) | Forced convection is less dependent on temperature |
| Flow Pattern | Vertical flow along surfaces | Directional based on forcing mechanism | Forced flow can be optimized for specific components |
| Fiabilité | Passive, always present | Requires power and maintenance | Natural convection provides baseline cooling |
| Space Requirements | Requires clearance for air circulation | Requires space for air movers and ducting | Forced systems need more planning |
Convection Enhancement Techniques
Surface Area Augmentation
Increasing effective surface area through:
Fins and Extended Surfaces
– Pin fins: Omnidirectional airflow, 150-300% area increase
– Plate fins: Directional airflow, 200-500% area increase
– Corrugated surfaces: Moderate enhancement, 50-150% area increaseSurface Roughening
– Micro-texturing: 5-15% effective area increase
– Dimpled surfaces: 10-30% increase plus boundary layer effects
– Grooved patterns: 15-40% increase with directional benefits
Flow Manipulation
Improving airflow characteristics through:
Forced Air Systems
– Fans: Directional airflow, 200-600% h improvement
– Blowers: High-pressure flow, 300-800% h improvement
– Compressed air jets: Targeted cooling, 400-1000% local h improvementFlow Path Optimization
– Baffles: Direct air to critical components
– Venturi effects: Accelerate air over specific surfaces
– Vortex generators: Create turbulence for boundary layer disruption
Surface Modifications
Altering surface properties to enhance convection:
Emissivity Treatments
– Black oxide: Increases emissivity to 0.7-0.9
– Anodizing: Controlled emissivity from 0.4-0.9
– Paints and coatings: Customizable emissivity up to 0.98Wettability Control
– Hydrophilic coatings: Enhance liquid cooling
– Hydrophobic surfaces: Prevent condensation issues
– Patterned wettability: Directed condensate flow
Practical Implementation Example
For a rodless pneumatic cylinder operating in a high-temperature environment:
| Enhancement Method | Implementation | h Improvement | Temperature Reduction |
|---|---|---|---|
| Pin Fins (6mm) | Aluminum clip-on fins, 10mm spacing | 180% | 12°C |
| Directed Airflow | 80mm, 2W DC fan at 1.5 m/s | 320% | 18°C |
| Surface Treatment | Black anodizing | 40% | 3°C |
| Combined Approach | All methods integrated | 450% | 24°C |
Nusselt Number Correlation for Design Calculations
For engineering calculations, the Nusselt number4 (Nu) provides a dimensionless approach to convection:
Nu = hL/k
Où ?
- L = Characteristic length
- k = Fluid thermal conductivity
For forced convection over a flat plate:
Nu = 0.664Re^(1/2)Pr^(1/3) (laminar flow)
Nu = 0.037Re^(4/5)Pr^(1/3) (turbulent flow)
Où ?
- Re = Reynolds number (velocity × length × density / viscosity)
- Pr = Prandtl number (specific heat × viscosity / thermal conductivity)
These correlations allow engineers to predict convection coefficients for different configurations and optimize cooling strategies accordingly.
Modèle d'efficacité du rayonnement : Quand le rayonnement thermique est-il important dans les systèmes pneumatiques ?
Radiation is often overlooked in pneumatic system thermal management, but it can account for 15-30% of total heat transfer in many applications. Understanding when and how to optimize radiative heat transfer is crucial for comprehensive thermal management.
Radiation heat transfer follows the Stefan-Boltzmann Law5: Q = εσA(T₁⁴-T₂⁴), where ε is surface emissivity, σ is the Stefan-Boltzmann constant, A is surface area, and T₁ and T₂ are absolute temperatures of the emitting surface and surroundings. Radiation efficiency in pneumatic systems depends primarily on surface emissivity, temperature differential, and view factors between components and their environment.
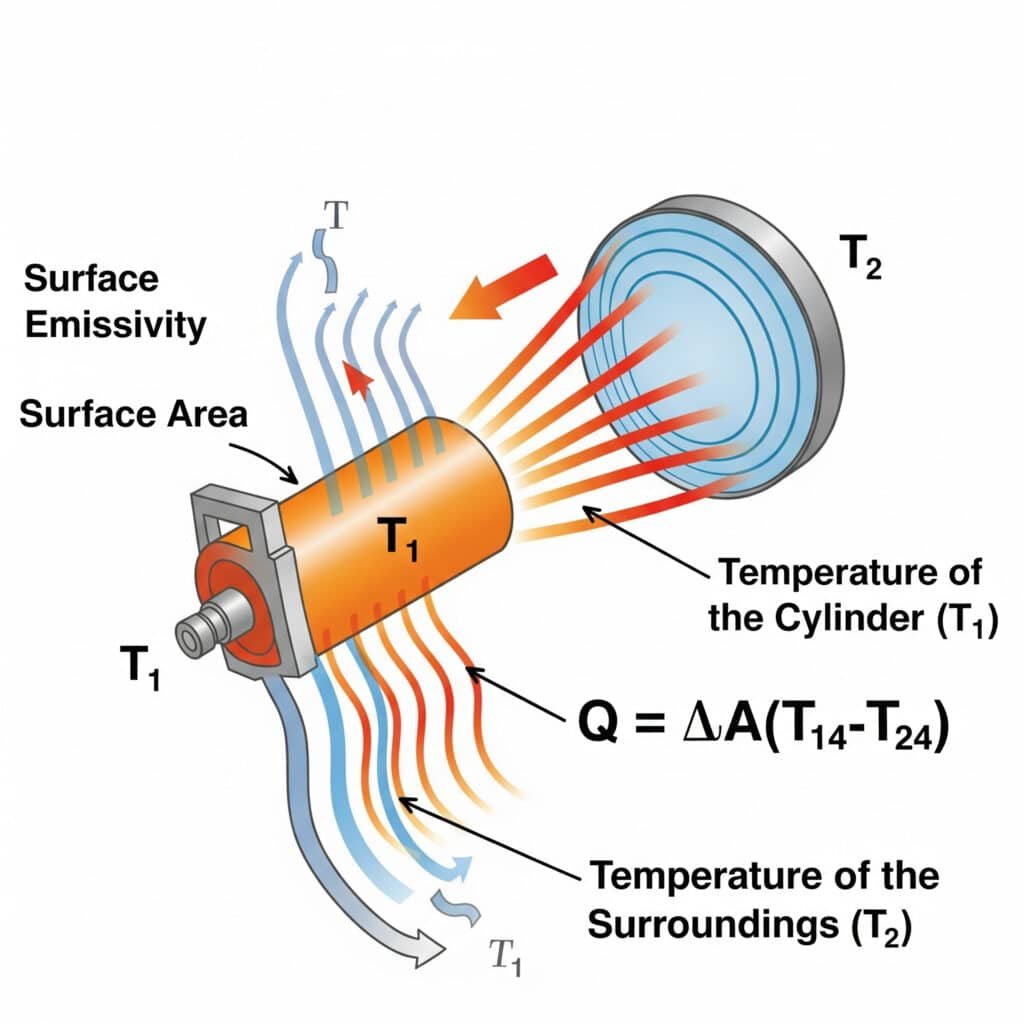
I recently helped a semiconductor equipment manufacturer in Oregon resolve overheating issues with their precision rodless cylinders. Their engineers had focused exclusively on conduction and convection but overlooked radiation. By applying a high-emissivity coating (increasing ε from 0.11 to 0.92), we enhanced radiative heat transfer by over 700%. This simple, passive solution reduced operating temperatures by 9°C without any moving parts or energy consumption—a critical requirement in their cleanroom environment.
Radiation Heat Transfer Fundamentals
The basic equation governing radiative heat transfer is:
Q = εσA(T₁⁴-T₂⁴)
Où ?
- Q = Taux de transfert de chaleur (W)
- ε = Emissivity (dimensionless, 0-1)
- σ = Stefan-Boltzmann constant (5.67 × 10⁻⁸ W/m²·K⁴)
- A = Surface area (m²)
- T₁ = Surface absolute temperature (K)
- T₂ = Surroundings absolute temperature (K)
Surface Emissivity Values for Common Pneumatic Materials
| Material/Surface | Emissivity (ε) | Radiation Efficiency | Enhancement Potential |
|---|---|---|---|
| Polished Aluminum | 0.04-0.06 | Very Poor | >1500% improvement possible |
| Anodized Aluminum | 0.7-0.9 | Excellent | Already optimized |
| Stainless Steel (polished) | 0.07-0.14 | Pauvre | >600% improvement possible |
| Stainless Steel (oxidized) | 0.6-0.85 | Bon | Moderate improvement possible |
| Steel (polished) | 0.07-0.10 | Pauvre | >900% improvement possible |
| Steel (oxidized) | 0.7-0.9 | Excellent | Already optimized |
| Painted Surfaces | 0.8-0.98 | Excellent | Already optimized |
| PTFE (white) | 0.8-0.9 | Excellent | Already optimized |
| Caoutchouc nitrile | 0.86-0.94 | Excellent | Already optimized |
View Factor Considerations
Radiation exchange depends not just on emissivity but also on geometric relationships between surfaces:
F₁₂ = Fraction of radiation leaving surface 1 that strikes surface 2
For complex geometries, view factors can be calculated using:
- Analytical solutions for simple geometries
- View factor algebra for combining known solutions
- Numerical methods for complex arrangements
- Empirical approximations for practical engineering
Temperature Dependence of Radiation
The fourth-power temperature relationship makes radiation particularly effective at higher temperatures:
| Surface Temperature | Percentage of Heat Transfer by Radiation* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Assuming natural convection conditions, ε = 0.8, 25°C ambient
Radiation Efficiency Enhancement Strategies
Based on my experience with industrial pneumatic systems, here are the most effective approaches for improving radiation heat transfer:
Surface Emissivity Modification
High-Emissivity Coatings
– Black anodizing for aluminum (ε ≈ 0.8-0.9)
– Black oxide for steel (ε ≈ 0.7-0.8)
– Specialty ceramic coatings (ε ≈ 0.9-0.98)Surface Texturing
– Micro-roughening increases effective emissivity
– Porous surfaces enhance radiative properties
– Combined emissivity/convection enhancements
Environmental Optimization
Surroundings Temperature Management
– Shielding from hot equipment/processes
– Cool walls/ceilings for better radiation exchange
– Reflective barriers to direct radiation to cooler surfacesView Factor Improvement
– Orientation to maximize exposure to cool surfaces
– Removal of blocking objects
– Reflectors to improve radiation exchange with cooler areas
Case Study: Radiation Enhancement in Precision Pneumatics
For a high-precision rodless cylinder in a cleanroom environment:
| Paramètres | Conception originale | Radiation-Enhanced Design | Amélioration |
|---|---|---|---|
| Surface Material | Polished Aluminum (ε ≈ 0.06) | Ceramic-Coated Aluminum (ε ≈ 0.94) | 1467% increase in emissivity |
| Radiation Heat Transfer | 2.1W | 32.7W | 1457% increase in radiation |
| Température de fonctionnement | 68°C | 59°C | 9°C reduction |
| Component Life | 8 months | >24 months | 3× improvement |
| Coût de la mise en œuvre | – | $175 per cylinder | 4.2 month payback |
Radiation vs. Other Heat Transfer Modes
Understanding when radiation dominates is crucial for efficient thermal management:
| Condition | Conduction Dominance | Convection Dominance | Radiation Dominance |
|---|---|---|---|
| Plage de température | Low to High | Low to Medium | Medium to High |
| Material Properties | High k materials | Low k, high surface area | High ε surfaces |
| Environmental Factors | Good thermal contact | Moving air, fans | Large temperature differential |
| Space Constraints | Tight packaging | Open air flow | View to cooler surroundings |
| Meilleures applications | Component interfaces | General cooling | Hot surfaces, vacuum, still air |
Conclusion
Mastering heat transfer principles—conduction coefficient calculation, convection enhancement methods, and radiation efficiency modeling—provides the foundation for effective thermal management in pneumatic systems. By applying these principles, you can reduce operating temperatures, extend component life, and improve energy efficiency while ensuring reliable operation even in challenging environments.
FAQ sur le transfert de chaleur dans les systèmes pneumatiques
Quelle est l'augmentation de température typique dans les cylindres pneumatiques en cours de fonctionnement ?
Les vérins pneumatiques subissent généralement des hausses de température de 20 à 40°C au-dessus de la température ambiante pendant leur fonctionnement continu. Cette augmentation résulte du frottement entre les joints et les parois du cylindre, du réchauffement de l'air par compression et de la conversion du travail mécanique en chaleur. Les vérins sans tige subissent souvent des hausses de température plus importantes (30-50°C) en raison de leurs systèmes d'étanchéité plus complexes et de la concentration de la chaleur dans l'ensemble palier/joint.
Comment la pression de fonctionnement affecte-t-elle la production de chaleur dans les systèmes pneumatiques ?
La pression de fonctionnement a un impact significatif sur la production de chaleur, les pressions plus élevées créant plus de chaleur par le biais de plusieurs mécanismes. Chaque augmentation de 1 bar de la pression de fonctionnement augmente généralement la production de chaleur de 8-12% en raison des forces de frottement plus importantes entre les joints et les surfaces, de l'échauffement plus important dû à la compression et de l'augmentation des pertes liées aux fuites. Cette relation est approximativement linéaire dans les plages de fonctionnement normales (3-10 bar).
What’s the optimal cooling approach for pneumatic components in different environments?
L'approche optimale du refroidissement varie en fonction de l'environnement : dans les environnements propres et à température modérée (15-30°C), la convection naturelle avec un espacement adéquat des composants est souvent suffisante. Dans les environnements à haute température (30-50°C), la convection forcée à l'aide de ventilateurs ou d'air comprimé devient nécessaire. Dans des conditions extrêmement chaudes (>50°C) ou lorsque la circulation de l'air est limitée, des méthodes de refroidissement actives telles que les refroidisseurs thermoélectriques ou le refroidissement par liquide peuvent être nécessaires. Dans tous les cas, l'optimisation du rayonnement par des surfaces à forte émissivité permet un refroidissement passif supplémentaire.
Comment calculer le transfert de chaleur total d'un composant pneumatique ?
Calculer le transfert de chaleur total en additionnant les contributions de chaque mécanisme : Qtotal = Qconduction + Qconvection + Qrayonnement. Pour la conduction, utilisez Q = kA(T₁-T₂)/L pour chaque chemin de chaleur. Pour la convection, on utilise Q = hA(Ts-T∞) avec les coefficients de convection appropriés. Pour le rayonnement, on utilise Q = εσA(T₁⁴-T₂⁴). Dans la plupart des applications pneumatiques industrielles fonctionnant à 30-80°C, la répartition approximative est la suivante : 20-40% pour la conduction, 40-70% pour la convection et 10-30% pour le rayonnement.
What’s the relationship between temperature and pneumatic component life?
La durée de vie des composants diminue de façon exponentielle avec l'augmentation de la température, suivant une relation d'Arrhenius modifiée. En règle générale, chaque augmentation de 10°C de la température de fonctionnement réduit la durée de vie des joints et des composants de 40-50%. Cela signifie qu'un composant fonctionnant à 70°C peut ne durer qu'un tiers de la durée de vie du même composant à 50°C. Cette relation est particulièrement critique pour les composants en polymère tels que les joints, les roulements et les garnitures, qui déterminent souvent l'intervalle de maintenance des systèmes pneumatiques.
-
Provides a foundational explanation of Fourier’s Law, the fundamental principle that describes how heat is conducted through solid materials based on their thermal conductivity and temperature gradient. ↩
-
Explains the function and types of Thermal Interface Materials (TIMs), which are used to fill microscopic air gaps between components to improve heat conduction and reduce thermal resistance. ↩
-
Details the principles of Newton’s Law of Cooling, which governs how objects cool by transferring heat to the surrounding fluid via convection, a key factor in system cooling design. ↩
-
Offers an in-depth look at the Nusselt number, a critical dimensionless quantity in fluid dynamics and heat transfer that represents the ratio of convective to conductive heat transfer across a boundary. ↩
-
Describes the Stefan-Boltzmann Law, the fundamental physical principle that quantifies the total energy radiated by a black body, which is essential for calculating heat loss from hot surfaces. ↩



