
Êtes-vous confronté à des vitesses de vérins pneumatiques incohérentes ou à des impacts de fin de course inattendus ? Ces problèmes courants sont souvent dus à une mauvaise compréhension de la cinématique des pistons. De nombreux ingénieurs se concentrent uniquement sur les exigences de force tout en négligeant les paramètres de mouvement critiques qui déterminent les performances du système.
Cinématique du piston1 ont un impact direct sur les performances des systèmes pneumatiques par le biais des relations pression-vitesse, des limites d'accélération et des exigences en matière d'amortissement. La compréhension de ces principes permet aux ingénieurs de dimensionner correctement les composants, de prévoir les profils de mouvement réels et de prévenir les défaillances prématurées des vérins sans tige et autres actionneurs pneumatiques.
Depuis plus de 15 ans que je travaille avec des systèmes pneumatiques chez Bepto, j'ai vu d'innombrables cas où la compréhension de ces principes fondamentaux a aidé les clients à résoudre des problèmes de performance persistants et à prolonger la durée de vie de l'équipement de 3 à 5 fois.
Table des matières
- Quelle est la pression nécessaire pour un mouvement à vitesse constante ?
- Comment calculer l'accélération maximale possible des vérins pneumatiques ?
- Quelle est l'importance de la durée d'amortissement et comment est-elle calculée ?
- Conclusion
- FAQ sur la cinématique des pistons dans les systèmes pneumatiques
Quelle est la pression nécessaire pour un mouvement à vitesse constante ?
De nombreux ingénieurs se contentent d'appliquer la pression maximale disponible à leurs systèmes pneumatiques, mais cette approche est inefficace et peut entraîner des mouvements saccadés, une usure excessive et un gaspillage d'énergie.
La pression requise pour un mouvement à vitesse constante dans un cylindre pneumatique est calculée en utilisant P = (F + Fr)/A, où P est la pression, F est la force de charge externe, Fr est la résistance au frottement et A est la surface du piston. Ce calcul garantit un fonctionnement souple et efficace sans pression excessive qui gaspille de l'énergie et accélère l'usure des composants.
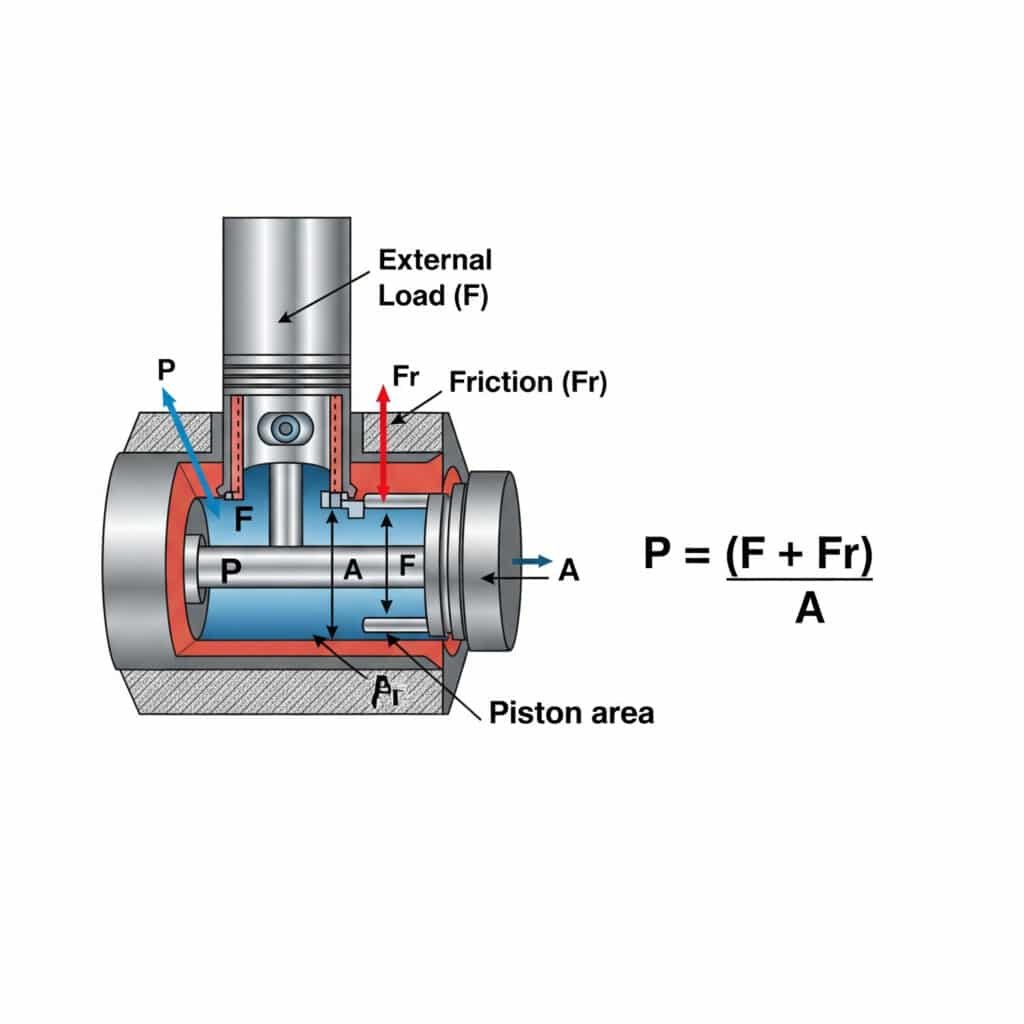
Comprendre les exigences en matière de pression pour un mouvement à vitesse constante a des implications pratiques pour la conception et le fonctionnement du système. Permettez-moi de les décomposer en idées concrètes.
Facteurs influençant la pression requise pour une vitesse constante
La pression nécessaire pour maintenir une vitesse constante dépend de plusieurs facteurs :
| Facteur | Impact sur l'exigence de pression | Considérations pratiques |
|---|---|---|
| Charge externe | Relation linéaire directe | Varie en fonction de l'orientation et des forces extérieures |
| Friction | Ajoute à la pression requise | Changements liés à l'usure des joints et à la lubrification |
| Zone du piston | Inversement proportionnel | Alésage plus important = pression requise plus faible |
| Restrictions de l'approvisionnement en air | Pertes de charge dans les conduites et les vannes | Dimensionner les composants pour une perte de charge minimale |
| Contre-pression | S'oppose à la motion | Tenir compte de la capacité d'écoulement des gaz d'échappement |
Calcul de la pression minimale pour un mouvement stable
Déterminer la pression minimale nécessaire pour obtenir un mouvement stable :
- Calculer la force nécessaire pour surmonter la charge externe
- Ajouter la force de frottement (typiquement 3-20% de la force maximale)
- Diviser par la surface effective du piston
- Ajouter un facteur de stabilité (typiquement 10-30%)
Par exemple, dans un vérin sans tige de 40 mm d'alésage avec une charge de 10 kg et un frottement de 15% :
| Paramètres | Calcul | Résultat |
|---|---|---|
| Force de charge | 10kg × 9,81m/s² | 98.1N |
| Force de frottement | 15% de force maximale à 6 bars | ~45N |
| Force totale | 98,1N + 45N | 143.1N |
| Zone du piston | π × (0,02m)² | 0.00126m² |
| Pression minimale | 143,1N ÷ 0,00126m² | 113 571 Pa (1,14 bar) |
| Avec 20% Facteur de stabilité | 1,14 bar × 1,2 | 1,37 bar |
Une application concrète : Économies d'énergie grâce à l'optimisation de la pression
L'année dernière, j'ai travaillé avec Robert, ingénieur de production dans une usine de fabrication de meubles du Michigan. Sa ligne d'assemblage automatisée utilisait des vérins sans tige fonctionnant à la pression d'alimentation maximale de 6 bars, quelle que soit la charge.
Après avoir analysé son application, nous avons déterminé que la plupart des mouvements ne nécessitaient que 2,5 à 3 bars pour un fonctionnement stable. En installant régulateurs de pression proportionnelleNous avons réduit la consommation d'air de 40% tout en conservant la même durée de cycle. Cela a permis d'économiser environ $12 000 euros par an en coûts énergétiques, tout en réduisant l'usure des joints et en prolongeant les intervalles de maintenance.
Relation vitesse-pression dans les systèmes réels
Dans la pratique, la relation entre la pression et la vitesse n'est pas parfaitement linéaire en raison des facteurs suivants :
- Restrictions de débit: Le dimensionnement des vannes et des orifices influe sur la vitesse maximale réalisable
- Effets de compressibilité: L'air est compressible, ce qui entraîne des retards d'accélération.
- Phénomènes de collage et de glissement: Les caractéristiques de frottement changent avec la vitesse
- Effets inertiels: L'accélération de la masse nécessite une force/pression supplémentaire
Comment calculer l'accélération maximale possible des vérins pneumatiques ?
Il est essentiel de comprendre les limites d'accélération pour éviter les chocs et les vibrations excessifs, ainsi que la défaillance prématurée des composants dans les systèmes pneumatiques.
L'accélération maximale possible dans un cylindre pneumatique est calculée à l'aide de a = (P × A - F - Fr)/m, où a est l'accélération, P est la pression, A est la surface du piston, F est la charge externe, Fr est la résistance au frottement et m est la masse en mouvement. Cette équation définit les limites physiques de la vitesse à laquelle un actionneur pneumatique peut démarrer ou arrêter un mouvement.
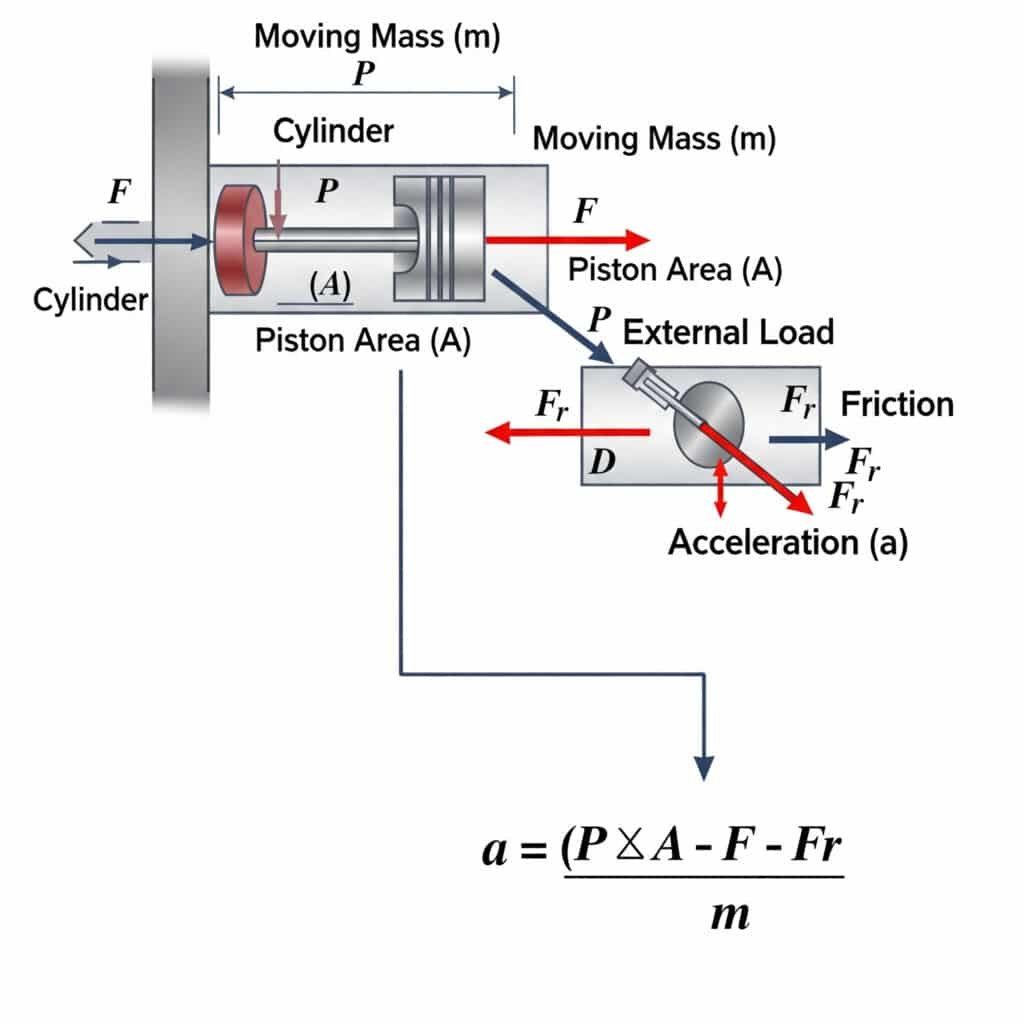
Les limites théoriques d'accélération ont des implications pratiques importantes pour la conception des systèmes et la sélection des composants.
Dérivation de l'équation limite d'accélération
L'équation de la limite d'accélération est la suivante Deuxième loi de Newton2 (F = ma) :
- La force nette disponible pour l'accélération est : Fnet = Fpression - Fcharge - Ffriction
- Fpression = P × A
- Par conséquent : a = Fnet/m = (P × A - F - Fr)/m
Limites d'accélération pratiques pour différents types de cylindres
Les différentes conceptions de cylindres ont des limites d'accélération pratiques différentes :
| Type de cylindre | Accélération maximale typique | Facteurs limitants |
|---|---|---|
| Cylindre à tige standard | 10-15 m/s² | Flambage de la tige, charges sur les roulements |
| Cylindre sans tige (magnétique) | 8-12 m/s² | Force de couplage magnétique |
| Cylindre sans tige (mécanique) | 15-25 m/s² | Conception des joints/roulements, frottement interne |
| Cylindre de guidage | 20-30 m/s² | Rigidité du système de guidage, capacité de charge |
| Cylindre d'impact | 50-100+ m/s² | Spécialement conçu pour les fortes accélérations |
Considérations sur la masse dans les calculs d'accélération
Lors du calcul de l'accélération, il est essentiel d'inclure toutes les masses en mouvement :
- Assemblage du piston: Comprend le piston, les joints et les éléments de connexion
- Masse de la charge: Charge externe déplacée
- Masse effective de l'air en mouvement: Souvent négligeable, mais important dans les applications à grande vitesse
- Masse supplémentaire due aux composants de montage: Supports, capteurs, etc.
J'ai un jour aidé un client en France qui connaissait de mystérieuses défaillances dans son système de vérins sans tige. Le cylindre était correctement dimensionné pour une charge de 15 kg, mais il tombait systématiquement en panne après quelques milliers de cycles.
Après enquête, nous avons découvert qu'il avait négligé de prendre en compte la masse de 12 kg de la plaque de montage et des accessoires. La masse réelle en mouvement était presque le double de ce qu'il avait calculé, provoquant des forces d'accélération qui dépassaient les limites de conception du vérin. Après le passage à un cylindre plus grand, les défaillances ont complètement cessé.
Méthodes de contrôle de l'accélération
Contrôler l'accélération dans des limites sûres :
- Vannes de régulation de débit: Limiter le débit lors du mouvement initial
- Vannes proportionnelles: Assurer une montée en pression contrôlée
- Accélération en plusieurs étapes: Utiliser des augmentations de pression par paliers
- Amortissement mécanique: Ajouter des amortisseurs externes
- Contrôle électronique: Utilisation systèmes servo-pneumatiques3 avec retour d'information sur l'accélération
Quelle est l'importance de la durée d'amortissement et comment est-elle calculée ?
Un amortissement correct en fin de course est essentiel pour prévenir les dommages dus aux chocs, réduire le bruit et prolonger la durée de vie des vérins pneumatiques. La compréhension du temps d'amortissement aide les ingénieurs à concevoir des systèmes qui équilibrent le temps de cycle et la longévité des composants.
Le temps d'amortissement des vérins pneumatiques est calculé à l'aide de l'équation t = √(2s/a), où t est le temps, s la longueur de la course d'amortissement et a la décélération. Ce temps représente le temps nécessaire pour décélérer en toute sécurité la masse en mouvement avant l'impact, ce qui est essentiel pour éviter d'endommager le vérin et les composants qui y sont fixés.

Examinons les aspects pratiques du calcul du temps de calage et leurs implications pour la conception du système.
La physique du coussin pneumatique
Amortissement pneumatique fonctionne grâce à une compression contrôlée de l'air et à un échappement restreint :
- Lorsque le piston pénètre dans la chambre d'amortissement, la trajectoire d'échappement est restreinte.
- L'air emprisonné se comprime, créant une contre-pression croissante.
- Cette contre-pression crée une force contraire qui décélère le piston
- Le profil de décélération dépend de la conception et du réglage du coussin.
Calcul du temps de calage optimal
Le temps d'amortissement optimal permet d'équilibrer la prévention des impacts et l'efficacité du temps de cycle :
| Paramètres | Formule | Exemple |
|---|---|---|
| Distance d'amortissement | Basé sur la conception du cylindre | 15 mm (typique pour un alésage de 40 mm) |
| Décélération requise | a = v²/(2s) | Pour v=0,5m/s, s=15mm : a = 8,33m/s². |
| Temps d'amortissement | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Accroissement de la pression | P = P₀(V₀/V)^γ | Dépend de la géométrie de la chambre du coussin |
Facteurs affectant la performance de l'amortissement
Plusieurs facteurs influencent les performances réelles de l'amortissement :
- Conception du joint d'étanchéité: Affecte les fuites d'air lors de l'amortissement
- Réglage de la soupape d'aiguille: Contrôle le taux de restriction des gaz d'échappement
- Masse en mouvement: Les charges plus lourdes nécessitent un temps d'amortissement plus long
- Vitesse d'approche: Des vitesses plus élevées nécessitent une plus grande distance de calage
- Pression de service: Affecte la contre-force maximale disponible
Les types de rembourrage et leurs applications
Différents mécanismes d'amortissement conviennent à différentes applications :
| Type de rembourrage | Caractéristiques | Meilleures applications |
|---|---|---|
| Amortissement fixe | Simple, non réglable | Charges légères, fonctionnement régulier |
| Coussin réglable | Accordable avec des vannes à aiguille | Charges variables, applications flexibles |
| Amortissement auto-ajustable | S'adapte à différentes conditions | Changement de vitesse et de charge |
| Amortisseurs externes | Absorption d'énergie élevée | Charges lourdes, vitesses élevées |
| Amortissement électronique | Décélération contrôlée avec précision | Systèmes servo-pneumatiques |
Étude de cas : Optimisation de l'amortissement dans les applications à cycle élevé
J'ai récemment travaillé avec Thomas, ingénieur concepteur chez un fabricant de composants automobiles en Allemagne. Sa ligne d'assemblage utilisait des vérins sans tige fonctionnant à 45 cycles par minute, mais elle connaissait des défaillances fréquentes des joints et des dommages au niveau des supports de montage.
L'analyse a révélé que le temps d'amortissement était trop court pour la masse en mouvement, provoquant des forces d'impact de près de 3G à chaque fin de course. En augmentant la course d'amortissement de 12 mm à 20 mm et en optimisant les réglages de la vanne à aiguille, nous avons allongé le temps d'amortissement de 0,04 s à 0,07 s.
Ce changement apparemment minime a permis de réduire les forces d'impact de plus de 60%, d'éliminer complètement les dommages causés au support et de prolonger la durée de vie des joints de 3 mois à plus d'un an, tout en maintenant le temps de cycle requis.
Procédure pratique de réglage des coussins d'air
Pour une performance optimale de l'amortissement dans les cylindres sans tige :
- Démarrer avec les vannes d'amortissement complètement ouvertes (restriction minimale)
- Fermer progressivement la soupape d'amortissement jusqu'à ce que la décélération se fasse en douceur.
- Essai avec les charges minimales et maximales prévues
- Vérifier la performance de l'amorti sur toute la plage de vitesse
- Écouter les bruits d'impact qui indiquent un amortissement insuffisant
- Mesurer le temps de décélération réel pour confirmer les calculs
Conclusion
Comprendre les principes de la cinématique des pistons - des exigences de pression pour une vitesse constante aux limites d'accélération et aux calculs de temps d'amortissement - est essentiel pour concevoir des systèmes pneumatiques efficaces et fiables. En appliquant ces principes à vos applications de vérins sans tige, vous pouvez optimiser les performances, réduire la consommation d'énergie et prolonger de manière significative la durée de vie des composants.
FAQ sur la cinématique des pistons dans les systèmes pneumatiques
Quelle est la pression nécessaire pour une vitesse de rotation donnée ?
La pression nécessaire dépend de la charge, du frottement et de la surface du cylindre. Elle se calcule à l'aide de P = (F + Fr)/A, où F est la force de la charge externe, Fr est la résistance au frottement et A est la surface du piston. Pour un vérin sans tige typique déplaçant une charge de 10 kg à l'horizontale, vous aurez besoin d'environ 1,5 à 2 bars pour un mouvement stable à des vitesses modérées.
Quelle est la vitesse d'accélération d'un cylindre pneumatique ?
L'accélération maximale d'un vérin pneumatique est calculée à l'aide de a = (P × A - F - Fr)/m. Les vérins sans tige typiques peuvent atteindre une accélération de 10 à 25 m/s² en fonction de leur conception. Cela signifie qu'une vitesse de 0,5 m/s est atteinte en 20 à 50 millisecondes environ dans des conditions optimales.
Quels sont les facteurs qui limitent la vitesse maximale d'un cylindre sans tige ?
La vitesse maximale est limitée par la capacité de débit de la valve, le volume d'alimentation en air, le dimensionnement de l'orifice, les capacités d'amortissement et la conception du joint. La plupart des vérins sans tige standard sont conçus pour des vitesses maximales de 0,8 à 1,5 m/s, bien que les modèles spécialisés à grande vitesse puissent atteindre 2 à 3 m/s.
Comment calculer l'amortissement adéquat pour mon application ?
Calculez le calage approprié en déterminant l'énergie cinétique (KE = ½mv²) de votre charge en mouvement et en vous assurant que votre système de calage peut absorber cette énergie. Le temps de calage doit être calculé en utilisant t = √(2s/a), où s est la distance de calage et a le taux de décélération souhaité.
Que se passe-t-il si mon vérin pneumatique accélère trop rapidement ?
Une accélération excessive peut entraîner des contraintes mécaniques sur les composants de montage, une usure prématurée des joints, une augmentation des vibrations et du bruit, un risque de déplacement ou d'endommagement de la charge et une réduction de la précision du système. Elle peut également entraîner des mouvements saccadés qui affectent la qualité des produits dans les applications de précision.
Comment l'orientation de la charge affecte-t-elle la pression nécessaire au mouvement ?
L'orientation de la charge a un impact significatif sur les exigences en matière de pression. Les charges verticales se déplaçant contre la gravité nécessitent une pression supplémentaire pour surmonter la force gravitationnelle (P = F/A + Fg/A + Fr/A). Les charges horizontales ne doivent surmonter que le frottement et l'inertie. Les charges inclinées se situent entre ces deux extrêmes en fonction du sinus de l'angle.
-
Fournit une explication fondamentale de la cinématique, la branche de la mécanique qui décrit le mouvement des objets sans tenir compte des forces qui causent le mouvement.
électronique, ce qui permet un contrôle pneumatique avancé. ↩ -
Détaille la deuxième loi de Newton (F=ma), le principe fondamental de la physique qui relie la force agissant sur un objet à sa masse et à son accélération, et qui est à la base de tous les calculs dynamiques. ↩
-
Décrit la servopneumatique, une technologie de contrôle avancée qui associe la puissance de la pneumatique à la précision du contrôle électronique en boucle fermée pour obtenir des profils de positionnement et de mouvement extrêmement précis. ↩



