Vos systèmes pneumatiques sont-ils confrontés à des vitesses de cylindre lentes, à des mouvements incohérents ou à une force insuffisante ? Ces problèmes courants sont souvent dus à un coupable mal compris : la résistance à l'écoulement. De nombreux ingénieurs dimensionnent leurs composants pneumatiques en se basant uniquement sur les exigences de pression et de force, sans tenir compte de l'impact critique de la résistance à l'écoulement sur les performances réelles.
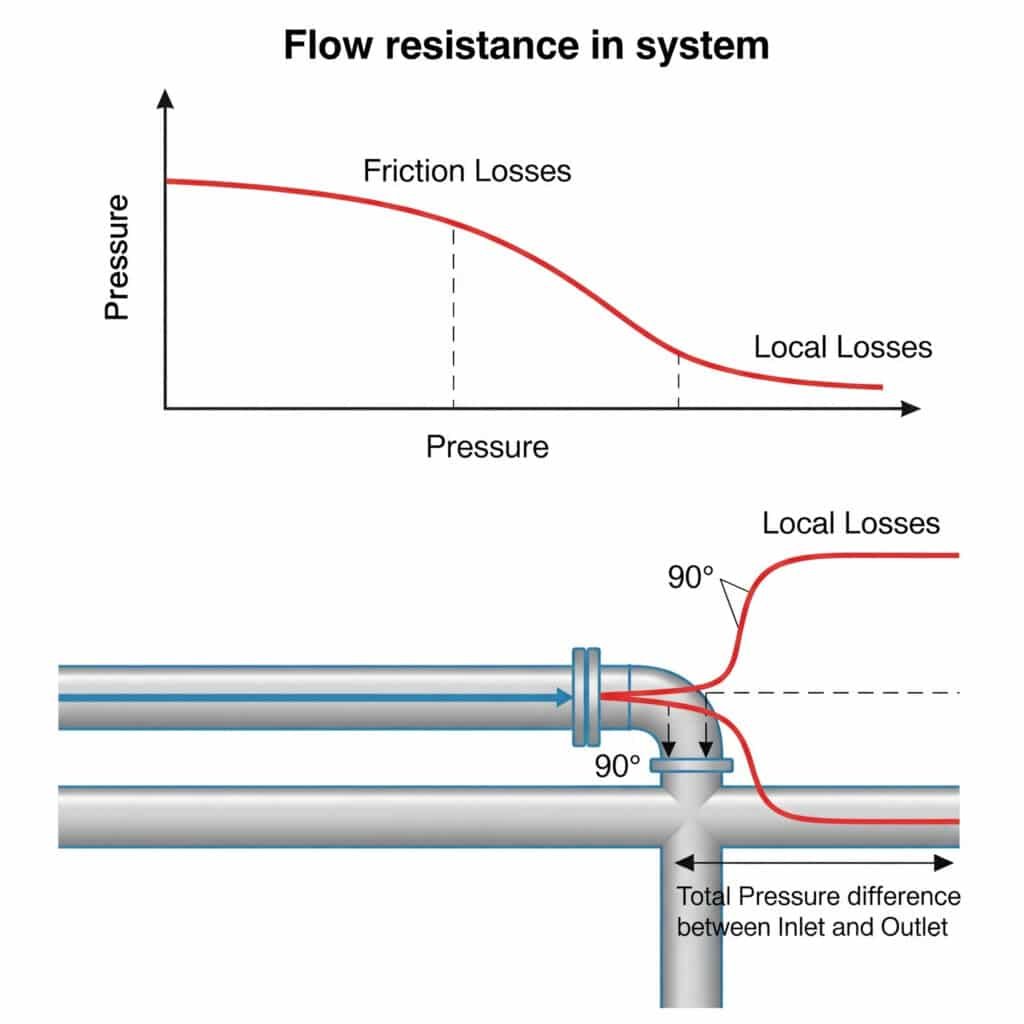
La résistance à l'écoulement dans les systèmes pneumatiques crée des pertes de charge qui réduisent la force disponible, limitent la vitesse maximale et provoquent des mouvements incohérents. Cette résistance provient à la fois du frottement le long des conduites droites (pertes par frottement) et des perturbations au niveau des raccords, des coudes et des vannes (pertes locales). Ensemble, ces résistances peuvent réduire les performances réelles du système de 20-50% par rapport aux calculs théoriques.
Depuis plus de 15 ans que je travaille avec des systèmes pneumatiques chez Bepto, j'ai vu d'innombrables cas où la compréhension et la prise en compte de la résistance à l'écoulement ont transformé des systèmes peu performants en opérations fiables et efficaces. Permettez-moi de partager ce que j'ai appris sur le calcul et la minimisation de ces obstacles cachés à la performance.
Table des matières
- Comment calculer les pertes par frottement dans les lignes pneumatiques ?
- Pourquoi la méthode de la longueur équivalente est-elle essentielle pour une conception précise des systèmes ?
- Que se passe-t-il lorsque l'air circule dans des sections à alésage réduit ?
- Conclusion
- FAQ sur la résistance à l'écoulement dans les systèmes pneumatiques
Comment calculer les pertes par frottement dans les lignes pneumatiques ?
Les pertes par frottement dans les tuyaux et tubes rectilignes sont à la base des calculs de résistance à l'écoulement, mais de nombreux ingénieurs s'appuient sur des règles empiriques trop simples qui conduisent à des systèmes sous-dimensionnés.
Les pertes par frottement dans les conduites pneumatiques sont calculées à l'aide de la formule suivante Équation de Darcy-Weisbach1ΔP = λ(L/D)(ρv²/2), où λ est le facteur de frottement, L la longueur du tuyau, D le diamètre du tuyau, ρ la densité de l'air et v la vitesse d'écoulement. Pour les systèmes pneumatiques, le facteur de frottement λ varie en fonction de Nombre de Reynolds2 et la rugosité relative, et est généralement déterminée à l'aide de tables de correspondance ou de l'outil Diagramme de Moody3.
La compréhension des pertes par frottement a des implications pratiques pour la conception et le dépannage des systèmes. Permettez-moi de vous présenter des idées concrètes.
Utilisation efficace des tableaux de facteurs de friction
Le facteur de frottement (λ) est le paramètre clé dans le calcul des pertes de charge, mais la détermination de sa valeur nécessite la prise en compte des conditions d'écoulement :
| Régime d'écoulement | Nombre de Reynolds (Re) | Détermination du facteur de friction |
|---|---|---|
| Écoulement laminaire | Re < 2000 | λ = 64/Re |
| Flux transitoire | 2000 < Re < 4000 | Peu fiable - éviter de concevoir dans cette gamme |
| Écoulement turbulent | Re > 4000 | Utiliser des tables de conversion basées sur la rugosité relative (ε/D) |
Tableau de consultation du facteur de friction pratique
Pour les écoulements turbulents dans les systèmes pneumatiques, utilisez ce tableau simplifié :
| Matériau du tube | Rugosité relative (ε/D) | Facteur de friction (λ) à des nombres de Reynolds courants |
|---|---|---|
| Re = 10 000 | ||
| Tubes lisses (PVC, polyuréthane) | 0.0001 – 0.0005 | 0.031 |
| Tubes en aluminium | 0.001 – 0.002 | 0.035 |
| Acier galvanisé | 0.003 – 0.005 | 0.042 |
| Acier rouillé | 0.01 – 0.05 | 0.054 |
Calcul de la perte de charge dans les systèmes pneumatiques réels
Prenons un exemple concret :
| Paramètres | Valeur/Calcul | Exemple |
|---|---|---|
| Diamètre du tube (D) | Diamètre interne | 8mm (0.008m) |
| Longueur du tuyau (L) | Longueur totale de la ligne droite | 5m |
| Débit (Q) | À partir des exigences du système | 20 litres standard/seconde |
| Densité de l'air (ρ) | A la pression de service | 7,2 kg/m³ à 6 bar |
| Vitesse d'écoulement (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Nombre de Reynolds (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1 273 600 |
| Rugosité relative | Pour les tubes en polyuréthane | 0.0003 |
| Facteur de friction (λ) | A partir du tableau de consultation | 0.017 |
| Perte de charge (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Application dans le monde réel : Résoudre les problèmes de vitesse de rotation des cylindres
L'année dernière, j'ai travaillé avec Sarah, ingénieur de fabrication dans une entreprise d'équipement d'emballage du Wisconsin. Son système de cylindres sans tige ne fonctionnait qu'à 60% de la vitesse prévue, malgré un cylindre de taille correcte et une pression d'alimentation adéquate.
Après avoir analysé son système, j'ai découvert qu'elle utilisait des tubes de 6 mm pour une application à haut débit. Les pertes par frottement provoquaient une chute de pression de 2,1 bars, ce qui réduisait considérablement la force et la vitesse disponibles. En passant à un tube de 10 mm, nous avons réduit la perte de charge à 0,4 bar, et son système a immédiatement atteint les performances requises sans aucune autre modification.
Facteurs affectant les pertes par frottement dans les systèmes réels
Plusieurs facteurs influencent les pertes par frottement réelles :
- Température de l'air: Des températures plus élevées augmentent la viscosité et le frottement
- Contamination: La saleté et l'huile peuvent augmenter la rugosité effective
- Cintrage de tubes: La micro-déformation des tubes cintrés augmente la résistance
- Détérioration due à l'âge: La corrosion et les dépôts augmentent la rugosité au fil du temps
- Pression de service: Des pressions plus élevées augmentent la densité et les pertes
Pourquoi la méthode de la longueur équivalente est-elle essentielle pour une conception précise des systèmes ?
Les pertes locales au niveau des raccords, des vannes et des coudes dépassent souvent les pertes par frottement dans les conduites droites. Pourtant, de nombreux ingénieurs les ignorent ou utilisent des méthodes d'estimation rudimentaires qui entraînent des problèmes de performance.
La méthode de la longueur équivalente convertit les pertes locales dues aux raccords et aux vannes en une longueur équivalente de tuyau droit qui causerait la même perte de charge. Cette longueur est calculée en utilisant Le = K(D/λ), où Le est la longueur équivalente, K est l'indice de perte de charge. coefficient de perte locale4D est le diamètre du tuyau et λ est le facteur de friction. Cette méthode simplifie les calculs et permet de prévoir avec plus de précision les performances du système.
Voyons comment appliquer efficacement cette méthode à la conception de systèmes pneumatiques.
Tableaux des longueurs équivalentes pour les composants pneumatiques courants
Voici un tableau de référence pratique pour les composants pneumatiques courants :
| Composant | Valeur K | Longueur équivalente (Le/D) |
|---|---|---|
| Coude à 90° (pointu) | 0.9 | 30 |
| Coude 90° (rayon standard) | 0.3 | 10 |
| Coude à 45 | 0.2 | 7 |
| Jonction en T (flux de passage) | 0.3 | 10 |
| Jonction en T (flux de dérivation) | 1.0 | 33 |
| Vanne à bille (complètement ouverte) | 0.1 | 3 |
| Vanne à guillotine (complètement ouverte) | 0.2 | 7 |
| Raccord rapide | 0.4-0.8 | 13-27 |
| Clapet anti-retour | 1.5-2.5 | 50-83 |
| Vanne de régulation de débit standard | 1.0-3.0 | 33-100 |
Application de la méthode de la longueur équivalente
Pour utiliser cette méthode de manière efficace :
- Identifier tous les composants de votre circuit pneumatique
- Déterminer la valeur K ou le rapport de longueur équivalent (Le/D) pour chaque composant.
- Calculer la longueur équivalente en multipliant par le diamètre du tuyau
- Additionner toutes les longueurs équivalentes à la longueur réelle du tuyau droit
- Utilisez la longueur effective totale dans vos calculs de perte par frottement.
Par exemple, un système composé de 5 m de tuyau droit de 8 mm, de quatre coudes de 90°, d'une jonction en T et de deux raccords rapides :
| Composant | Quantité | Le/D | Longueur équivalente |
|---|---|---|---|
| Coudes à 90 | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| Jonction en T | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Raccords rapides | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Longueur totale équivalente | 0.72m | ||
| Longueur droite réelle | 5.00m | ||
| Longueur effective totale | 5.72m |
Cela signifie que votre système de 5 m se comporte en fait comme un système de 5,72 m en raison des pertes locales, soit une augmentation de 14,41 TTP3T de la longueur effective.
Étude de cas : Optimisation du placement des vannes dans les systèmes d'assemblage
J'ai récemment aidé Miguel, ingénieur en automatisation dans une usine d'assemblage électronique en Arizona. Son système de prélèvement et de déplacement présentait des mouvements incohérents et des variations de temps de cycle, malgré l'utilisation de composants de haute qualité.
L'analyse a révélé que son collecteur de vannes était situé à 3 m des cylindres et que le circuit comprenait de nombreux raccords. Le calcul de la longueur équivalente a montré que la distance réelle de 3 m avait une longueur effective de 7,2 m en raison des pertes locales, soit plus du double de la distance en ligne droite !
En déplaçant le collecteur de vannes plus près des cylindres et en éliminant plusieurs raccords, nous avons réduit la longueur effective de 7,2 m à 2,1 m. Cela a permis de réduire la perte de charge de 701 TTP3T. Cela a permis de réduire la perte de charge de 70%, ce qui s'est traduit par un mouvement régulier et une réduction du temps de cycle de 15%.
Conseils pratiques pour minimiser les pertes locales
Pour réduire les pertes locales dans vos systèmes pneumatiques :
- Utiliser des coudes arrondis ou balayés au lieu de coudes brusques (réduit la valeur K de 67%)
- Minimiser le nombre de raccords en prévoyant des itinéraires plus directs
- Choisir des composants à faible friction utiliser, le cas échéant, des robinets à tournant sphérique à passage intégral
- Dimensionner correctement les raccords - les raccords sous-dimensionnés provoquent des pertes disproportionnées
- Placer les vannes à proximité des actionneurs pour minimiser la longueur effective du tube
Que se passe-t-il lorsque l'air circule dans des sections à alésage réduit ?
Les sections d'alésage réduites dans les circuits pneumatiques - telles que les vannes partiellement fermées, les raccords sous-dimensionnés ou les transitions de diamètre - créent des restrictions de débit significatives qui peuvent avoir un impact sévère sur les performances du système.
Lorsque l'air circule dans des sections réduites, chutes de pression5 se produisent selon la formule ΔP = ρ(v₂² - v₁²)/2, où v₁ est la vitesse avant la restriction et v₂ est la vitesse dans la restriction. Ce phénomène peut être compensé en utilisant le facteur de compensation du rapport d'alésage C = (1 - (d/D)⁴), où d est le diamètre réduit et D le diamètre d'origine. Ce facteur permet de prévoir les performances réelles du système et d'éviter de sous-dimensionner les composants.
Examinons les implications pratiques des sections d'alésage réduites et la manière d'en tenir compte dans la conception du système.
Calcul des chutes de pression aux transitions de diamètre
Lorsque l'air passe d'un diamètre plus grand à un diamètre plus petit, la perte de charge peut être calculée à l'aide de la formule suivante :
| Paramètres | Formule | Exemple |
|---|---|---|
| Diamètre d'origine (D) | Du cahier des charges | 10 mm |
| Diamètre réduit (d) | Du cahier des charges | 6 mm |
| Rapport d'alésage (d/D) | Division simple | 0.6 |
| Débit (Q) | À partir des exigences du système | 15 litres standard/seconde |
| Vitesse dans le tuyau d'origine (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Vitesse dans la section réduite (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Perte de charge (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Facteur de compensation (C) | C = (1 - (d/D)⁴) | 0.87 |
Scénarios courants de réduction de l'alésage et leur impact
Voici comment les différentes réductions d'alésage affectent la capacité de débit :
| Réduction de l'alésage | Réduction de la capacité d'écoulement | Augmentation de la perte de charge |
|---|---|---|
| 10mm à 8mm | 36% | 2.4× |
| 10mm à 6mm | 64% | 7.7× |
| 10mm à 4mm | 84% | 39× |
| 8mm à 6mm | 44% | 3.2× |
| 8mm à 4mm | 75% | 16× |
| 6mm à 4mm | 56% | 5.1× |
Ces chiffres montrent pourquoi des réductions de diamètre apparemment mineures peuvent avoir des effets considérables sur les performances du système.
L'effet cumulatif des restrictions multiples
Dans les circuits pneumatiques réels, plusieurs restrictions se produisent en série. Leur effet est cumulatif et peut être calculé à l'aide de :
- Convertir chaque restriction en son facteur C équivalent
- Calculer le facteur C total : Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Utilisez ce facteur total pour déterminer la réduction des performances globales du système.
Étude de cas : Résolution des problèmes d'inadéquation entre la vanne et l'actionneur
Le mois dernier, j'ai travaillé avec Thomas, responsable de la maintenance dans une usine de fabrication de meubles en Caroline du Nord. Son nouveau système de vérins sans tige fonctionnait à moins de la moitié de la vitesse prévue, malgré l'utilisation de la taille de valve recommandée par le fabricant.
L'enquête a révélé de multiples réductions d'alésage dans son circuit :
- Conduite d'alimentation de 10 mm vers les orifices de vanne de 8 mm (C₁ = 0,36)
- Orifices de vanne de 8 mm vers raccords de 6 mm (C₂ = 0,44)
- Raccords de 6 mm aux orifices de cylindre de 8 mm avec restrictions internes (C₃ = 0,32)
Le facteur de compensation total était Ctotal = 1 - (1-0.36)(1-0.44)(1-0.32) = 0.75, ce qui signifie que son système perdait 75% de sa capacité de débit théorique !
En passant à des composants correctement dimensionnés dans l'ensemble du système, nous avons éliminé ces restrictions et atteint les performances requises sans modifier la bouteille ou la pression d'alimentation.
Stratégies pratiques pour minimiser les pertes dues à la réduction des alésages
Réduire les pertes dues à la réduction des alésages :
- Dimensionner les composants de manière cohérente dans l'ensemble du circuit pneumatique
- Utiliser le plus grand diamètre de tube possible pour les applications à haut débit
- Attention aux restrictions concernant les composants interneset pas seulement les tailles de connexion
- Envisager des voies d'écoulement parallèles pour les besoins à haut débit
- Éliminer les adaptateurs et les transitions inutiles dans la mesure du possible
Le principe du "maillon faible" dans les systèmes pneumatiques
N'oubliez pas que les performances de votre système pneumatique sont limitées par le composant le plus restrictif. Un seul élément sous-dimensionné peut annuler les avantages de composants correctement dimensionnés ailleurs dans le système.
Par exemple, un système avec des tubes de 10 mm, des vannes de 10 mm, mais des raccords de 6 mm au niveau de la bouteille fonctionnera essentiellement de la même manière qu'un système avec des composants de 6 mm sur l'ensemble du système, mais à un coût plus élevé.
Conclusion
Il est essentiel de comprendre et de calculer correctement la résistance à l'écoulement - à l'aide de tableaux de facteurs de frottement, de méthodes de longueur équivalente et de compensation de l'alésage réduit - pour concevoir des systèmes pneumatiques qui fonctionnent comme prévu dans des conditions réelles. En appliquant ces méthodes de calcul et ces principes de conception, vous pouvez optimiser vos applications de vérins sans tige et autres systèmes pneumatiques pour obtenir des performances et une fiabilité maximales.
FAQ sur la résistance à l'écoulement dans les systèmes pneumatiques
Quelle est la perte de charge acceptable dans un système pneumatique ?
La perte de charge acceptable dépend des exigences de votre application, mais en règle générale, il convient de limiter la perte de charge totale à 10-15% de la pression d'alimentation pour un fonctionnement efficace. Pour un système de 6 bars, cela signifie que la perte de charge totale doit être inférieure à 0,6-0,9 bar. Les applications critiques peuvent nécessiter des pertes de charge encore plus faibles, de l'ordre de 5-8%, pour maintenir des performances constantes.
Quelle est la relation entre le diamètre du tube et la perte de charge ?
La perte de charge est inversement proportionnelle à la cinquième puissance du diamètre (D⁵) pour les écoulements turbulents dans les systèmes pneumatiques. Cela signifie qu'un doublement du diamètre du tube réduit la perte de charge d'environ 32 fois. Par exemple, passer d'un tube de 6 mm à un tube de 12 mm peut réduire la perte de charge de 1,5 bar à seulement 0,047 bar dans les mêmes conditions d'écoulement.
Comment déterminer la taille de tube adaptée à mon application pneumatique ?
Choisir la taille du tube en fonction du débit requis et de la perte de charge acceptable. Calculer le nombre de Reynolds et le facteur de friction, puis utiliser l'équation de Darcy-Weisbach pour déterminer la perte de charge pour différents diamètres. Choisissez le plus petit diamètre qui maintient la perte de charge dans des limites acceptables (généralement <10% de la pression d'alimentation) tout en tenant compte des contraintes d'espace et de coût.
Qu'est-ce qui crée le plus de restrictions : un coude à 90° ou 5 mètres de tuyau droit ?
Un coude à 90° crée généralement une résistance équivalente à 30 diamètres de tube droit. Pour un tube de 8 mm, un coude aigu équivaut à environ 240 mm (30 × 8 mm) de tube droit. Cela signifie que 5 mètres de tube droit créent environ 21 fois plus de restriction qu'un seul coude. Cependant, les systèmes contiennent souvent plusieurs coudes et raccords, dont l'effet cumulé peut dépasser les pertes de longueur droite.
Comment les raccords rapides affectent-ils les performances du système ?
Les raccords rapides standard introduisent généralement une perte locale équivalente à 15-25 diamètres de tube droit. Plus important encore, de nombreux raccords rapides ont des restrictions internes inférieures à leur taille nominale. Un raccord rapide de "10 mm" peut avoir une restriction interne de seulement 7-8 mm, créant une réduction de l'alésage qui peut réduire la capacité d'écoulement de 50-70% à ce point.
Quel est l'impact des vannes de régulation de débit partiellement fermées sur les performances du système ?
Un régulateur de débit fermé à 50% de son diamètre total ne réduit pas le débit de 50% seulement, mais d'environ 75% en raison de la relation non linéaire entre le diamètre et la capacité d'écoulement. La perte de charge augmente en fonction du carré de la variation de vitesse, de sorte que la réduction de moitié du diamètre effectif augmente la perte de charge d'environ 16 fois dans les mêmes conditions de débit.
-
Fournit une analyse détaillée de l'équation de Darcy-Weisbach, une formule fondamentale et largement utilisée dans la dynamique des fluides pour calculer la perte de pression due au frottement dans une conduite. ↩
-
Offre une définition claire du nombre de Reynolds, une quantité critique sans dimension utilisée pour prédire les modèles d'écoulement (laminaires ou turbulents) dans différentes situations d'écoulement de fluides. ↩
-
Présente le diagramme de Moody, un graphique complet qui trace le facteur de frottement de Darcy en fonction du nombre de Reynolds et de la rugosité relative, qui est l'outil standard des ingénieurs pour déterminer la perte de charge dans les tuyaux. ↩
-
Explique le concept de valeur K, ou coefficient de perte locale, un nombre sans dimension utilisé pour caractériser la perte de pression dans un raccord de tuyauterie ou une vanne dans le cadre de la méthode de la longueur équivalente. ↩
-
Détaille la physique de la chute de pression qui se produit lorsqu'un fluide passe à travers une restriction (un orifice), en se basant sur les principes de l'équation de continuité et du principe de Bernoulli. ↩



