Le cauchemar de tout ingénieur de maintenance est la défaillance inattendue d'un équipement. Lorsque les machines vibrent à leur fréquence naturelle, des dommages catastrophiques peuvent survenir en quelques minutes. J'ai vu ce problème coûter aux entreprises des milliers de dollars en temps d'arrêt.
Résonance vibratoire1 se produit lorsqu'une force extérieure correspond à la fréquence naturelle d'un système, ce qui provoque des oscillations amplifiées susceptibles d'endommager l'équipement. Il est essentiel de comprendre et de contrôler ce phénomène pour prévenir les pannes et prolonger la durée de vie des machines.
Permettez-moi de vous raconter une petite histoire. L'année dernière, un client allemand m'a appelé en panique. Sa ligne de production s'était arrêtée à cause d'un cylindre sans tige vibrait violemment. Le problème ? La résonance. À la fin de cet article, vous saurez comment identifier et prévenir des problèmes similaires dans vos systèmes.
Table des matières
- Formule de la fréquence naturelle : Comment calculer les points vulnérables de votre système ?
- Le modèle du printemps de masse : Pourquoi cette approche simplifiée est-elle si précieuse ?
- Optimisation du ratio d'amortissement : Quelles sont les expériences qui donnent les meilleurs résultats ?
- Conclusion
- FAQ sur la résonance vibratoire
Formule de la fréquence naturelle : Comment calculer les points vulnérables de votre système ?
Comprendre la fréquence naturelle de votre équipement est la première étape vers la prévention des problèmes de résonance. Cette valeur critique détermine le moment où votre système est le plus vulnérable aux problèmes de vibration.
Le fréquence naturelle2 (fn) d'un système peut être calculée à l'aide de la formule suivante : fn = (1/2π) × √(k/m), où k est le coefficient de rigidité et m la masse. Ce calcul révèle la fréquence à laquelle votre système résonnera s'il est excité par des forces externes correspondantes.
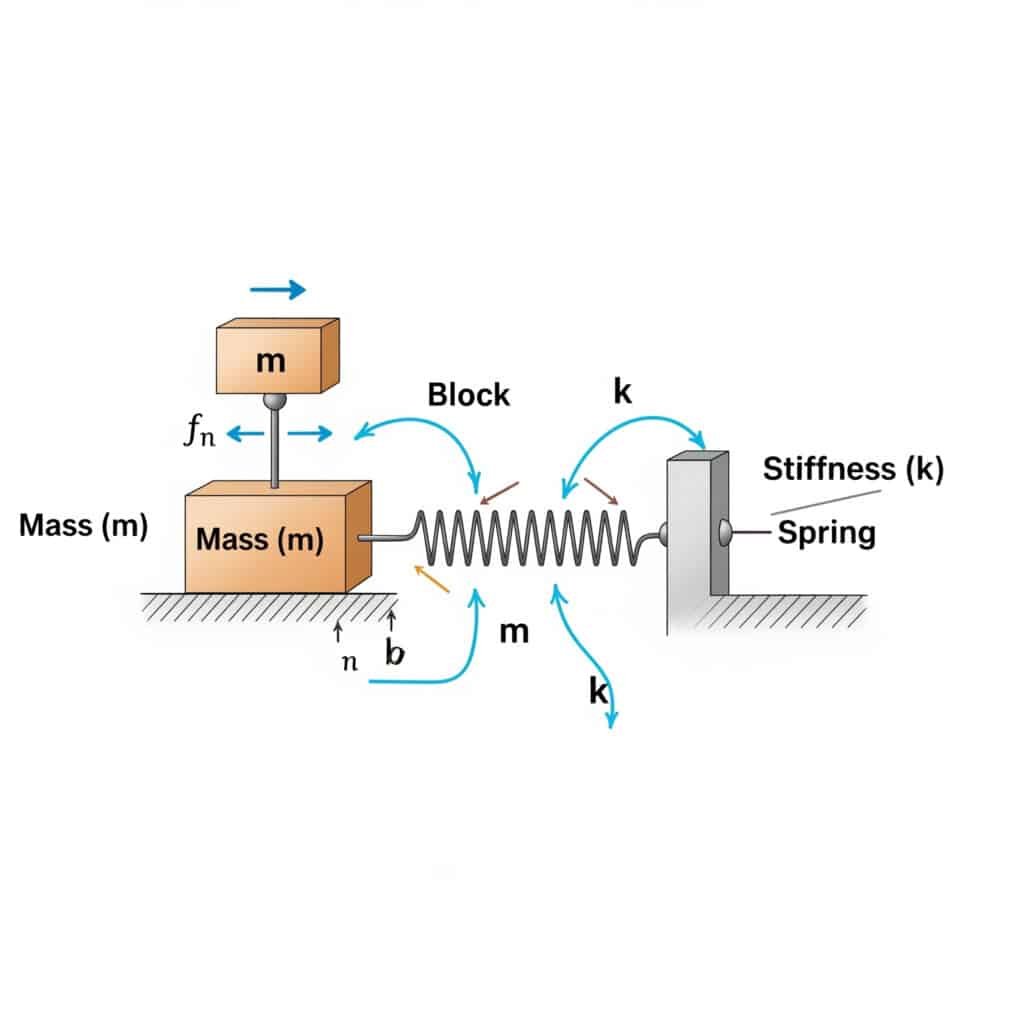
Lorsque j'ai visité une usine de fabrication en Suisse, j'ai remarqué que les vérins pneumatiques sans tige tombaient en panne prématurément. L'équipe de maintenance n'avait pas calculé la fréquence naturelle de leur installation. Après avoir appliqué cette formule, nous avons identifié que leur vitesse de fonctionnement était dangereusement proche de la fréquence naturelle du système.
Applications pratiques du calcul de la fréquence naturelle
La formule de la fréquence naturelle n'est pas seulement théorique, elle a des applications directes dans divers environnements industriels :
- Sélection des équipements: Choisir des composants dont les fréquences propres sont éloignées de vos conditions d'utilisation
- Maintenance préventive: Programmation des inspections sur la base des profils de risque vibratoire
- Dépannage: Identifier la cause première des vibrations inattendues
Valeurs courantes de la fréquence naturelle des composants industriels
| Composant | Gamme de fréquences naturelles typiques (Hz) |
|---|---|
| Cylindres sans tige | 10-50 Hz |
| Supports de montage | 20-100 Hz |
| Structures de soutien | 5-30 Hz |
| Vannes de contrôle | 40-200 Hz |
Facteurs critiques affectant la fréquence naturelle
Le calcul de la fréquence naturelle semble simple, mais plusieurs facteurs peuvent compliquer les applications dans le monde réel :
- Distribution de masse non uniforme: La plupart des composants industriels n'ont pas une masse parfaitement répartie.
- Rigidité variable: Les composants peuvent avoir une rigidité différente dans différentes directions.
- Points de connexion: La façon dont les composants sont montés influe considérablement sur leurs caractéristiques vibratoires
- Effets de la température: Les propriétés de masse et de rigidité peuvent varier en fonction de la température.
Le modèle du printemps de masse : Pourquoi cette approche simplifiée est-elle si précieuse ?
Le modèle masse-ressort fournit un cadre intuitif pour comprendre les systèmes vibratoires complexes. Il réduit les machines compliquées à des éléments de base que les ingénieurs peuvent facilement analyser.
Le modèle masse-ressort3 simplifie l'analyse des vibrations en représentant les systèmes mécaniques comme des masses discrètes reliées par des ressorts. Cette approche permet aux ingénieurs de prévoir le comportement du système, d'identifier les problèmes de résonance potentiels et de développer des solutions efficaces sans avoir recours à des mathématiques complexes.
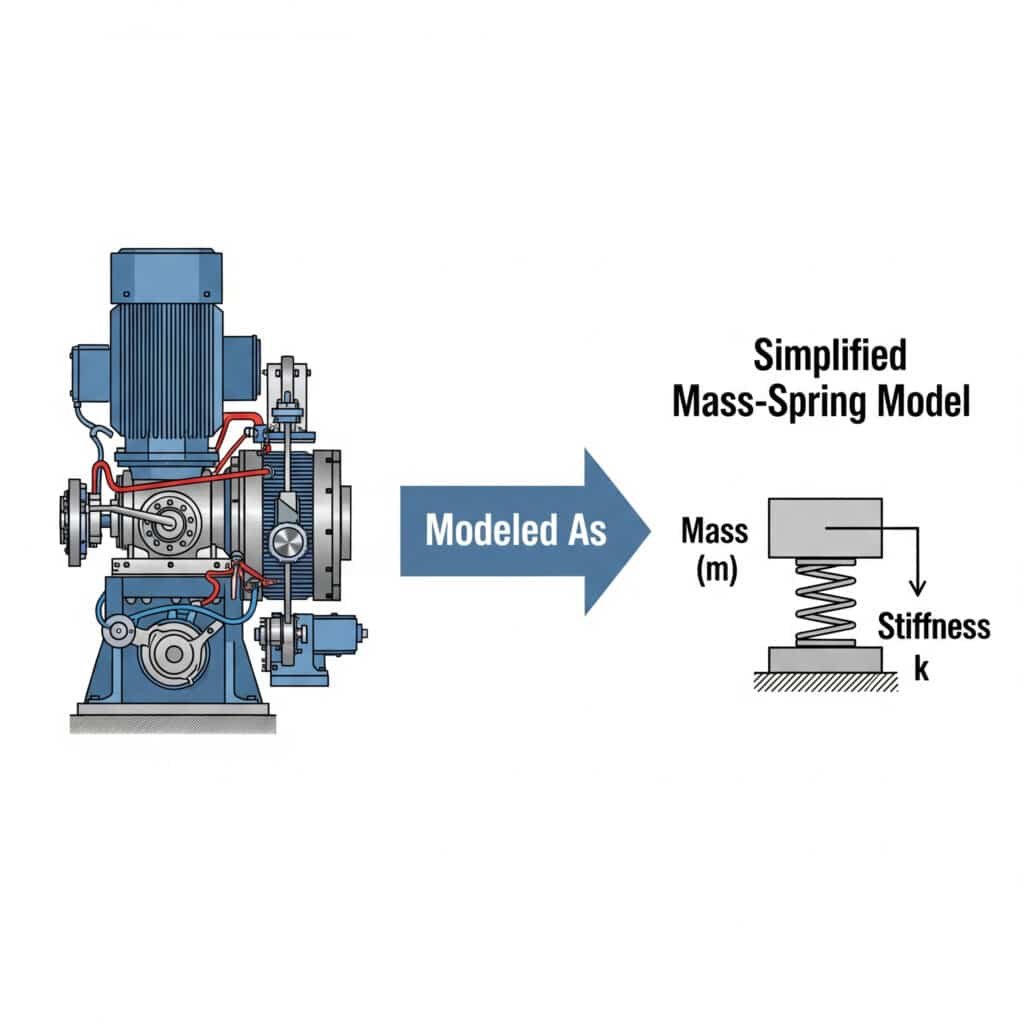
Je me souviens avoir travaillé avec un fabricant de pièces automobiles du Michigan qui ne comprenait pas pourquoi ses vérins guidés sans tige tombaient en panne. En modélisant leur système comme un simple arrangement masse-ressort, nous avons identifié que les supports de montage agissaient comme des ressorts involontaires, créant une condition de résonance.
Conversion de systèmes réels en modèles de masse-ressort
Pour appliquer cette approche à votre équipement :
- Identifier les masses clés: Déterminer quels sont les composants qui contribuent de manière significative au poids
- Localiser les éléments du ressort: Trouver des composants qui stockent et libèrent de l'énergie (ressorts réels, supports flexibles, etc.).
- Connexions cartographiques: Documenter l'interaction entre les masses et les ressorts
- Simplifier: Combiner des éléments similaires pour créer un modèle gérable
Types de systèmes à ressort en masse
| Type de système | Description | Applications courantes |
|---|---|---|
| Simple DOF | Une masse avec un ressort | Vérins pneumatiques simples |
| Multi-DOF | Masses multiples avec ressorts multiples | Machines complexes à composants multiples |
| En continu | DOF infini (nécessite une analyse différente) | Poutres, plaques et coquilles |
Considérations sur la modélisation avancée
Si le modèle masse-ressort de base est valable, plusieurs améliorations le rendent plus réaliste :
- Ajout d'amortisseurs: Les systèmes réels présentent toujours une dissipation d'énergie
- Prise en compte des non-linéarités: Les sources ne suivent pas toujours Loi de Hooke4 parfaitement
- Prise en compte des vibrations forcées: Les forces extérieures modifient le comportement du système
- Y compris les effets de couplage: Un mouvement dans une direction peut affecter d'autres directions
Optimisation du ratio d'amortissement : Quelles sont les expériences qui donnent les meilleurs résultats ?
L'amortissement est votre meilleure défense contre les problèmes de résonance. Trouver le rapport d'amortissement optimal par l'expérimentation peut améliorer considérablement les performances et la fiabilité du système.
Rapport d'amortissement5 Les expériences d'optimisation consistent à tester systématiquement différentes configurations d'amortissement afin de trouver l'équilibre idéal entre le contrôle des vibrations et la réactivité du système. Le taux d'amortissement optimal se situe généralement entre 0,2 et 0,7, ce qui permet de supprimer suffisamment de vibrations sans perte d'énergie excessive.
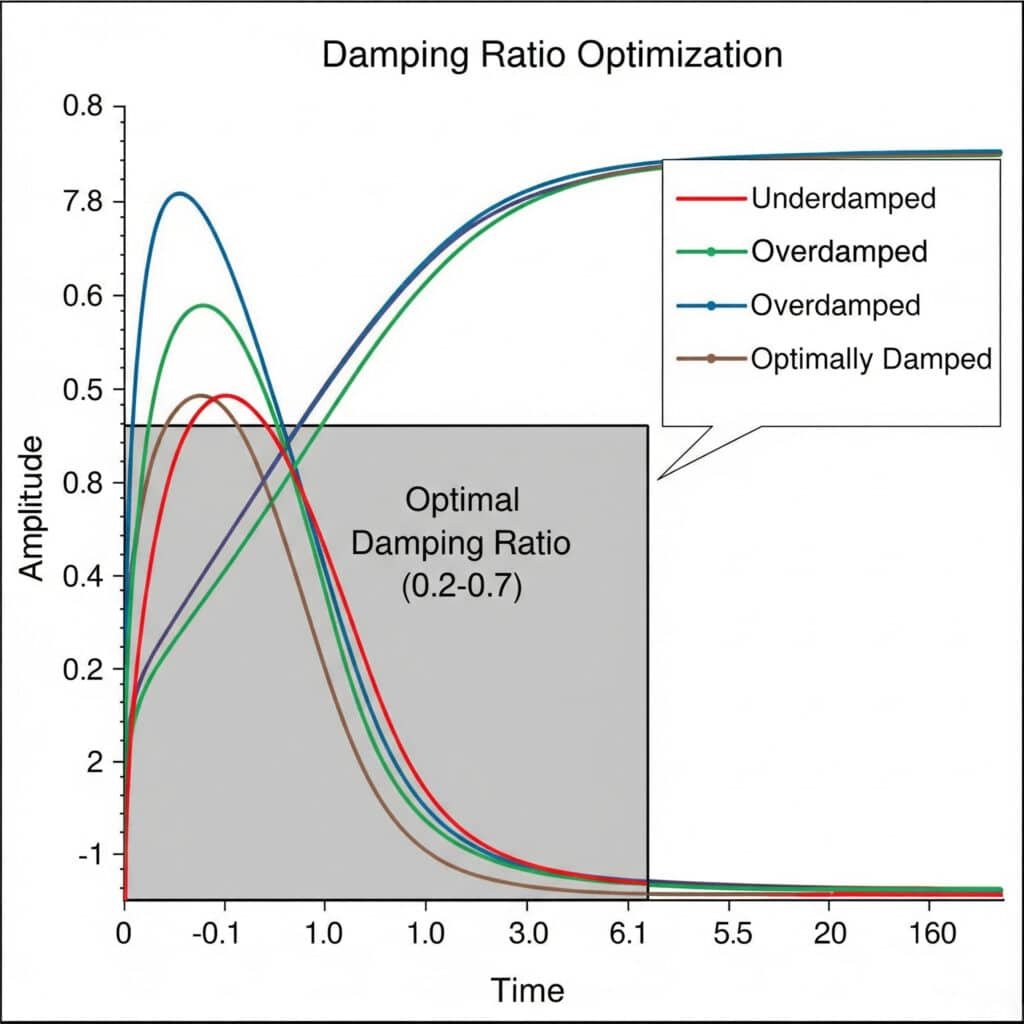
Le mois dernier, j'ai aidé un fabricant français d'équipements de transformation alimentaire à résoudre des problèmes persistants de vibrations dans ses cylindres magnétiques sans tige. Grâce à une série d'expériences sur le rapport d'amortissement, nous avons découvert que leur conception originale avait un rapport d'amortissement de seulement 0,05, bien trop faible pour éviter les problèmes de résonance.
Dispositif expérimental pour l'essai du taux d'amortissement
Mener des expériences d'optimisation de l'amortissement :
- Mesure de référence: Enregistrement de la réponse du système sans amortissement supplémentaire
- Tests incrémentaux: Ajouter des éléments d'amortissement par incréments contrôlés
- Mesure de la réponse: Mesure de l'amplitude, du temps de stabilisation et de la réponse en fréquence
- Analyse des données: Calculer le taux d'amortissement pour chaque configuration
- Validation: Vérifier les performances dans les conditions réelles d'utilisation
Comparaison des technologies d'amortissement
| Technologie d'amortissement | Avantages | Limites | Applications typiques |
|---|---|---|---|
| Amortisseurs visqueux | Performance prévisible, température stable | Nécessite un entretien, fuites potentielles | Machines lourdes, équipements de précision |
| Amortisseurs à friction | Une conception simple, un bon rapport qualité-prix | Usure dans le temps, comportement non linéaire | Supports structurels, machines de base |
| Amortissement des matériaux | Pas de pièces mobiles, compact | Plage de réglage limitée | Instruments de précision, isolation des vibrations |
| Amortissement actif | Adaptation aux conditions changeantes | Complexe, nécessite de l'énergie | Applications critiques, équipement à vitesse variable |
Optimisation de l'amortissement pour différentes conditions de fonctionnement
Le rapport d'amortissement idéal n'est pas universel - il dépend de votre application spécifique :
- Opérations à grande vitesse: Des rapports d'amortissement plus faibles (0,1-0,3) maintiennent la réactivité.
- Applications de précision: Des rapports d'amortissement plus élevés (0,5-0,7) assurent la stabilité.
- Systèmes à charge variable: Un amortissement adaptatif peut être nécessaire
- Environnements sensibles à la température: Envisager des matériaux amortissants aux propriétés stables
Étude de cas : Optimisation de l'amortissement des vérins sans tige
Lors de l'optimisation d'un vérin sans tige à double effet pour une machine d'emballage, nous avons testé cinq configurations d'amortissement différentes :
- Coussins d'extrémité standard: Rapport d'amortissement = 0,12
- Coussins allongés: Rapport d'amortissement = 0,25
- Amortisseurs externes: Taux d'amortissement = 0,41
- Supports de montage en composite: Taux d'amortissement = 0,38
- Approche combinée (3+4): Rapport d'amortissement = 0,53
L'approche combinée a donné les meilleurs résultats, réduisant l'amplitude des vibrations de 78% tout en maintenant des temps de réponse acceptables.
Conclusion
La compréhension de la résonance vibratoire par le calcul de la fréquence naturelle, la modélisation masse-ressort et l'optimisation du rapport d'amortissement est cruciale pour prévenir les pannes d'équipement. En appliquant ces principes, vous pouvez prolonger la durée de vie des machines, réduire les temps d'arrêt et améliorer les performances globales du système.
FAQ sur la résonance vibratoire
Qu'est-ce que la résonance vibratoire dans les équipements industriels ?
La résonance vibratoire se produit lorsqu'une force extérieure correspond à la fréquence naturelle d'un système, ce qui provoque des oscillations amplifiées. Dans les équipements industriels, ce phénomène peut entraîner des mouvements excessifs, la fatigue des composants et des défaillances catastrophiques s'il n'est pas correctement géré.
Comment puis-je savoir si mon système est en résonance ?
Recherchez des symptômes tels que des augmentations inexpliquées du bruit, des vibrations visibles à des vitesses spécifiques, des défaillances prématurées de composants et une dégradation des performances qui se produit à des points de fonctionnement constants. Les outils d'analyse des vibrations peuvent confirmer les conditions de résonance.
Quelle est la différence entre une vibration forcée et une résonance ?
La vibration forcée se produit chaque fois qu'une force externe agit sur un système, tandis que la résonance est la condition spécifique lorsque cette fréquence forcée correspond à la fréquence naturelle du système, ce qui entraîne une réponse amplifiée. Toutes les résonances impliquent des vibrations forcées, mais toutes les vibrations forcées ne provoquent pas de résonance.
Comment la conception d'un vérin pneumatique sans tige affecte-t-elle ses caractéristiques vibratoires ?
La conception des vérins pneumatiques sans tige - avec leur chariot mobile, leur système d'étanchéité interne et leurs mécanismes de guidage - crée des défis uniques en matière de vibrations. Le profil allongé agit comme une poutre qui peut fléchir, la masse du chariot crée des forces d'inertie et les bandes d'étanchéité peuvent introduire des frottements variables.
Quelles modifications simples peuvent réduire la résonance dans les équipements existants ?
Pour les équipements existants qui connaissent des problèmes de résonance, il faut envisager d'ajouter de la masse pour modifier la fréquence naturelle, d'installer des amortisseurs externes, de modifier les méthodes de montage pour inclure l'isolation des vibrations ou d'ajuster les vitesses de fonctionnement pour éviter les fréquences de résonance.
-
Fournit une explication fondamentale de la résonance mécanique, souvent à l'aide d'exemples visuels, démontrant comment une petite force périodique peut produire des oscillations de grande amplitude dans un système. ↩
-
Offre un aperçu détaillé de la physique de la fréquence naturelle, la fréquence spécifique à laquelle un système tend à osciller en l'absence de toute force motrice ou d'amortissement. ↩
-
Explique les principes du modèle masse-ressort, une idéalisation fondamentale en physique et en ingénierie utilisée pour analyser des systèmes complexes qui présentent un mouvement harmonique simple. ↩
-
Détaille la loi de Hooke, un principe de physique qui stipule que la force nécessaire pour étendre ou comprimer un ressort sur une certaine distance est directement proportionnelle à cette distance. ↩
-
Décrit le taux d'amortissement, une mesure sans dimension qui définit la façon dont les oscillations d'un système diminuent après une perturbation, ce qui est essentiel pour contrôler la résonance. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська