Quel est le volume d'une sphère plate dans les applications de vérins pneumatiques ?

Série OSP-P Le vérin modulaire original sans tige — Vérin mécanique sans tige OSP

Les ingénieurs sont confrontés à une certaine confusion lorsqu'ils calculent les volumes des composants sphériques aplatis dans les systèmes de vérins pneumatiques sans tige. Des calculs de volume incorrects entraînent des erreurs de calcul de la pression et des défaillances du système.

Une sphère plate (sphéroïde oblate) a un volume V = (4/3)πa²b, où "a" est le rayon équatorial et "b" le rayon polaire. accumulateur pneumatique¹ et les applications de rembourrage.

Le mois dernier, j'ai aidé Andreas, un ingénieur concepteur allemand, dont le système de calage pneumatique a échoué parce qu'il avait utilisé le volume d'une sphère standard au lieu d'un sphéroïde oblat pour calculer les chambres d'accumulation aplaties.

Table des matières

Qu'est-ce qu'une sphère plate dans les applications pneumatiques ?
Comment calculer le volume d'une sphère plate ?
Où les sphères plates sont-elles utilisées dans les vérins sans tige ?
Comment l'aplatissement affecte-t-il le volume et la performance ?

Qu'est-ce qu'une sphère plate dans les applications pneumatiques ?

Une sphère plate, techniquement appelée sphéroïde oblate²La forme tridimensionnelle créée par la compression d'une sphère le long d'un axe est couramment utilisée dans les accumulateurs pneumatiques et les coussins d'air.

Une sphère plate résulte de l'aplatissement d'une sphère parfaite le long de son axe vertical, ce qui crée une section elliptique dont les rayons horizontaux et verticaux sont différents.

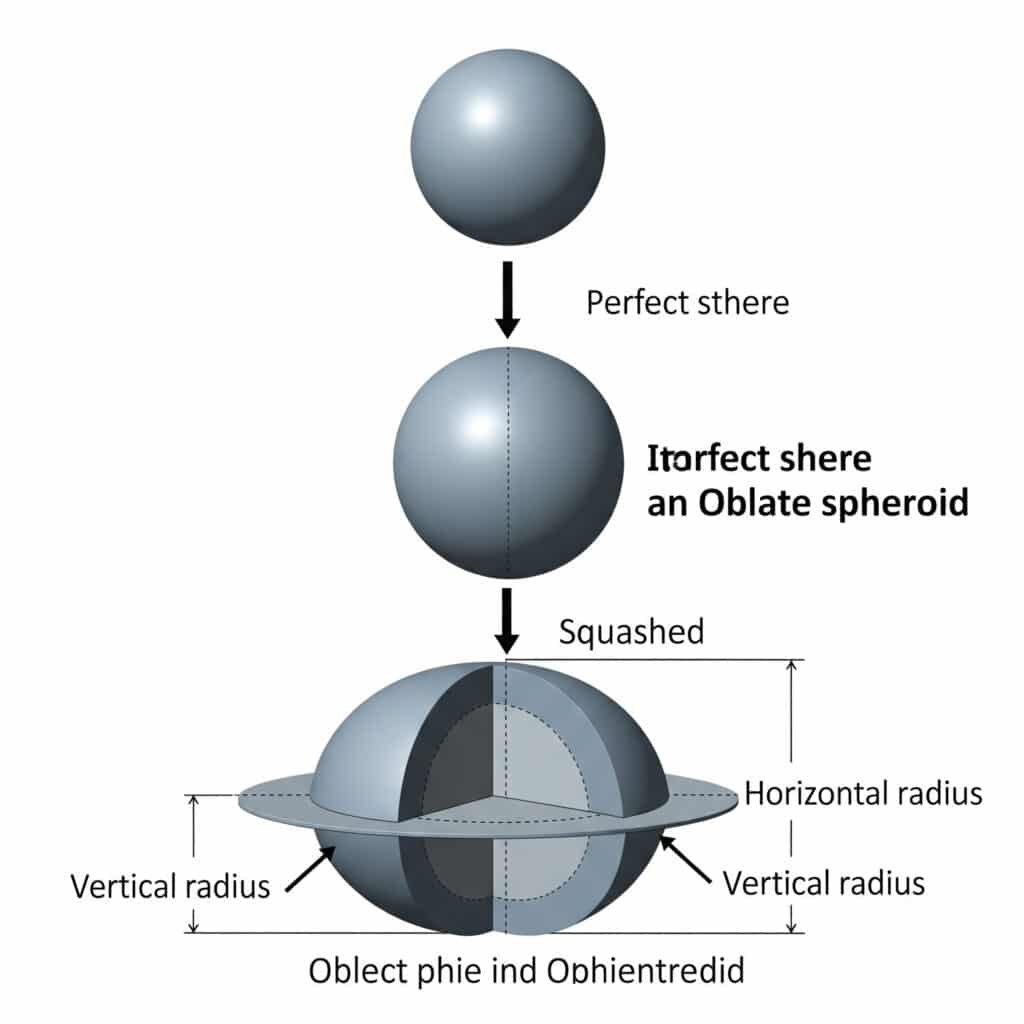
Diagramme en trois étapes illustrant la transformation d'une sphère parfaite en une sphère plate (sphéroïde oblate). Le processus montre que la sphère est écrasée, ce qui donne une forme dont la section transversale est mise en évidence et dont les rayons verticaux et horizontaux de différentes longueurs sont clairement indiqués. — Diagramme de sphère plate montrant une forme de sphéroïde oblate

Définition géométrique

Caractéristiques de la forme

Sphéroïde oblate: Terme technique géométrique
Sphère aplatie: Description industrielle commune
Profil elliptique: Vue en coupe
Symétrie de rotation: Autour de l'axe vertical

Dimensions des clés

Rayon équatorial (a): Rayon horizontal (plus grand)
Rayon polaire (b): Rayon vertical (plus petit)
Taux d'aplatissement: b/a < 1.0
Rapport d'aspect: Rapport entre la hauteur et la largeur

Sphère plate et sphère parfaite

Caractéristique	Sphère parfaite	Sphère plate
Forme	Rayon uniforme	Compression verticale
Formule de volume	(4/3)πr³	(4/3)πa²b
Coupe transversale	Cercle	Ellipse
Symétrie	Toutes les directions	Horizontal uniquement

Ratios d'aplatissement courants

Aplanissement de la lumière

Ratio: b/a = 0,8-0,9
Applications: Légères contraintes d'espace
Impact sur le volume: Réduction 10-20%
Performance: Effet minime

Aplatissement modéré

Ratio: b/a = 0,6-0,8
Applications: Modèles d'accumulateurs standard
Impact sur le volumeRéduction : 20-40%
Performance: Changements de pression perceptibles

Aplatissement lourd

Ratio: b/a = 0,3-0,6
Applications: Limitations sévères de l'espace
Impact sur le volume: Réduction 40-70%
Performance: Principales considérations en matière de conception

Applications pneumatiques

Chambres d'Accumulation

Je rencontre des sphères plates dans :

Installations soumises à des contraintes d'espace: Limites de hauteur
Modèles intégrés: Intégrés dans les bâtis des machines
Applications personnalisées: Exigences spécifiques en matière de volume
Projets de modernisation: Aménagement des espaces existants

Systèmes d'amortissement

Amortissement en fin de course: Applications de vérins sans tige
Absorption des chocs: Gestion de la charge d'impact
Régulation de la pression: Contrôle des opérations en douceur
Réduction du bruit: Fonctionnement plus silencieux du système

Considérations relatives à la fabrication

Méthodes de production

Dessin en profondeur: Formage de tôles
Hydroformage: Processus de façonnage de précision
Usinage: Composants personnalisés et uniques
Casting: Production en grande série

Sélection des matériaux

Acier: Applications à haute pression
Aluminium: Conceptions sensibles au poids
Acier inoxydable: Environnements corrosifs
Matériaux composites: Exigences spécifiques

Comment calculer le volume d'une sphère plate ?

Le calcul du volume d'une sphère plate nécessite l'utilisation de la formule du sphéroïde oblat en utilisant les mesures des rayons équatoriaux et polaires pour une conception précise du système pneumatique.

Utilisez la formule V = (4/3)πa²b où "a" est le rayon équatorial (horizontal) et "b" le rayon polaire (vertical) pour calculer avec précision le volume d'une sphère plate.

Ventilation de la formule de volume

Formule standard

V = (4/3)πa²b

V: Volume en unités cubiques
π: 3,14159 (constante mathématique)
a: Rayon équatorial (horizontal)
b: Rayon polaire (vertical)
4/3: Coefficient de volume de la sphéroïde

Composants de la formule

Zone équatoriale: πa² (section horizontale)
Mise à l'échelle polairefacteur b (compression verticale)
Coefficient de volume: 4/3 (constante géométrique)
Unités de résultat: Correspondre aux unités de rayon d'entrée cubées

Calcul étape par étape

Processus de mesure

Mesurer le diamètre équatorial: Dimension horizontale la plus large
Calculer le rayon équatorial: a = diamètre ÷ 2
Mesurer le diamètre polaire: Dimension verticale de la hauteur
Calculer le rayon polaire: b = hauteur ÷ 2
Appliquer la formule: V = (4/3)πa²b

Exemple de calcul

Pour un accumulateur pneumatique :

Diamètre équatorial: 100mm → a = 50mm
Diamètre polaire: 60mm → b = 30mm
Volume: V = (4/3)π(50)²(30)
Résultat: V = (4/3)π(2500)(30) = 314,159 mm³

Exemples de calcul de volume

Rayon équatorial	Rayon polaire	Ratio d'aplatissement	Volume	Comparaison avec la sphère
50 mm	50 mm	1.0	523 599 mm³	100% (sphère parfaite)
50 mm	40 mm	0.8	418 879 mm³	80%
50 mm	30 mm	0.6	314 159 mm³	60%
50 mm	20 mm	0.4	209 440 mm³	40%

Outils de calcul

Calcul manuel

Calculatrice scientifique: Avec la fonction π
Vérification de la formule: Double vérification des entrées
Cohérence des unités: Maintenir les mêmes unités partout
Précision: Calculer avec les décimales appropriées

Outils numériques

Logiciel d'ingénierie: Calculs de volume en CAO
Calculatrices en ligne: Outils sphéroïdes oblats
Formules de tableur: Calculs automatisés
Applications mobiles: Outils de calcul sur le terrain

Erreurs de calcul courantes

Erreurs de mesure

Rayon et diamètre: Utilisation d'une dimension erronée
Confusion des axes: Mélange de mesures horizontales et verticales
Incohérence de l'unité: mixage en mm ou en pouces
Perte de précision: Arrondi trop précoce

Erreurs de formule

Mauvaise formule: Utilisation de la sphère au lieu du sphéroïde
Inversion des paramètres: Échange des valeurs a et b
Erreurs de coefficient: Facteur 4/3 manquant
Approche π: Utilisation de la version 3.14 au lieu de la version 3.14159

Méthodes de vérification

Techniques de vérification croisée

Logiciel de CAO: Calcul du volume du modèle 3D
Déplacement de l'eau: Mesure du volume physique
Calculs multiples: Comparaison de différentes méthodes
Spécifications du fabricant: Données sur les volumes publiés

Contrôles de vraisemblance

Réduction du volume: La sphère doit être moins que parfaite
Aplanissement de la corrélation: Plus d'aplatissement = moins de volume
Vérification de l'unité: Les résultats correspondent à l'ampleur attendue
Adéquation de l'application: Le volume répond aux exigences du système

Lorsque j'ai aidé Maria, une conceptrice de systèmes pneumatiques espagnole, à calculer les volumes des accumulateurs pour son installation de vérins sans tige, nous avons découvert que ses calculs originaux utilisaient des formules de sphères au lieu de sphéroïdes oblats, ce qui entraînait une surestimation du volume de 35% et une performance inadéquate du système.

Où les sphères plates sont-elles utilisées dans les vérins sans tige ?

Les sphères plates apparaissent dans divers composants de vérins pneumatiques sans tige où les contraintes d'espace exigent une optimisation du volume tout en maintenant la fonctionnalité de l'appareil sous pression.

Les sphères plates sont couramment utilisées dans les chambres d'accumulateurs, les systèmes d'amortissement et les réservoirs sous pression intégrés dans les assemblages de cylindres sans tige lorsque les restrictions de hauteur limitent les conceptions sphériques standard.

Applications de l'accumulateur

Accumulateurs intégrés

Optimisation de l'espace: S'inscrire dans le cadre des machines
Efficacité en volume: Stockage maximal dans une hauteur limitée
Stabilité de la pression: Fonctionnement sans heurts lors des pics de demande
Intégration des systèmes: Intégré dans les bases de montage des cylindres

Installations de modernisation

Machines existantes: Limites de hauteur libre
Projets de mise à niveau: Ajouter l'accumulation à des systèmes plus anciens
Contraintes d'espace: Travailler dans le cadre de l'enveloppe de conception originale
Amélioration des performances: Amélioration de la réponse du système

Systèmes d'amortissement

Amortissement en fin de course

J'installe des coussins de sphère plate pour les :

Cylindres magnétiques sans tige: Décélération en douceur
Vérins guidés sans tige: Réduction de l'impact
Vérins sans tige à double effet: Amortissement bidirectionnel
Applications à grande vitesse: Absorption des chocs

Régulation de la pression

Lissage des flux: Éliminer les pics de pression
Réduction du bruit: Fonctionnement plus silencieux
Protection des composants: Réduction de l'usure et des contraintes
Stabilité du système: Des performances constantes

Composants spécialisés

Appareils à pression

Applications personnalisées: Exigences uniques en matière d'espace
Conceptions multifonctionnelles: Stockage et montage combinés
Systèmes modulaires: Configurations empilables
Accès à la maintenance: Modèles utilisables

Chambres de capteurs

Contrôle de la pression: Systèmes de mesure intégrés
Détection du débit: Applications de détection de vitesse
Diagnostic du système: Contrôle des performances
Systèmes de sécurité: Intégration de la décharge de pression

Considérations relatives à la conception

Contraintes spatiales

Application	Limite de hauteur	Aplatissement typique	Impact sur le volume
Montage sous le sol	50 mm	b/a = 0,3	Réduction 70%
Intégration des machines	100mm	b/a = 0,6	Réduction 40%
Applications de modernisation	150 mm	b/a = 0,8	Réduction 20%
Montage standard	200 mm et plus	b/a = 0,9	Réduction 10%

Exigences de performance

Pression nominale: Maintenir l'intégrité structurelle
Capacité en volume: Répondre à la demande du système
Caractéristiques de l'écoulement: Dimensionnement adéquat de l'entrée et de la sortie
Accès à la maintenance: Considérations relatives à l'aptitude au service

Exemples d'installation

Machines d'emballage

Application: Équipement de remplissage à grande vitesse
Contrainte: 40 mm de hauteur libre
Solution: Accumulateur fortement aplati (b/a = 0,25)
RésultatRéduction du volume, performances adéquates : 75%

Assemblage automobile

Application: Système de positionnement robotique
Contrainte: Intégration dans la base robotique
Solution: Aplatissement modéré (b/a = 0,7)
Résultat: 30% gain de place, maintien des performances

Transformation des aliments

Application: Système de cylindre sanitaire sans tige
Contrainte: Autorisation pour l'environnement de lavage
Solution: Conception personnalisée d'une sphère plate
Résultat: Classification IP69K³ avec un volume optimisé

Spécifications de fabrication

Tailles standard

Petit: 50mm équatorial, diverses dimensions polaires
Moyen: 100mm équatorial, variations de hauteur
Grandes dimensionsEquatorial de 200 mm, taille polaire sur mesure
Sur mesure: Dimensions spécifiques à l'application

Options de matériaux

Acier au carbone: Applications de pression standard
Acier inoxydable: Environnements corrosifs
Aluminium: Installations sensibles au poids
Composite: Exigences spécifiques

L'année dernière, j'ai travaillé avec Thomas, un constructeur de machines suisse, qui avait besoin de stocker des accumulateurs pour sa ligne d'emballage compacte. Les accumulateurs sphériques standard n'étant pas adaptés à la restriction de hauteur de 60 mm, nous avons conçu des accumulateurs sphériques plats avec un rapport b/a = 0,4, ce qui permet d'obtenir 60% du volume d'origine tout en respectant les contraintes d'espace.

Comment l'aplatissement affecte-t-il le volume et la performance ?

L'aplatissement réduit considérablement la capacité de volume tout en affectant la dynamique de la pression, les caractéristiques du débit et les performances globales du système dans les applications pneumatiques sans tige.

Chaque augmentation de 10% de l'aplatissement (diminution du rapport b/a) réduit le volume d'environ 10% et affecte la réponse à la pression, les schémas d'écoulement et l'efficacité du système dans les applications d'accumulateurs pneumatiques.

Analyse de l'impact en volume

Relations de réduction de volume

Rapport de volume = (b/a) pour les sphéroïdes oblongs

Relation linéaire: Le volume diminue proportionnellement à l'aplatissement
Impact prévisible: Facilité de calcul des variations de volume
Flexibilité de la conception: Choisir le taux d'aplatissement optimal
Compromis de performance: Équilibrer l'espace et la capacité

Changements de volume quantifiés

Ratio d'aplatissement (b/a)	Rétention du volume	Perte de volume	Adéquation de l'application
0.9	90%	10%	Excellent
0.8	80%	20%	Très bon
0.7	70%	30%	Bon
0.6	60%	40%	Juste
0.5	50%	50%	Pauvre
0.4	40%	60%	Très faible

Effets de la pression sur les performances

Caractéristiques de la réponse à la pression

Volume réduit: Changements de pression plus rapides
Sensibilité accrue: Plus réactif aux variations de débit
Augmentation du nombre de cyclistes: Cycles de charge/décharge plus fréquents
Instabilité du système: Oscillations de pression potentielle

Ajustements du calcul de la pression

P₁V₁ = P₂V₂ (Loi de Boyle⁴ s'applique)

Volume réduit: Pression plus élevée pour une même masse d'air
Variations de pression: Variations plus importantes pendant le fonctionnement
Dimensionnement du système: Compenser par une plus grande capacité du compresseur
Marges de sécurité: Exigences accrues en matière de pression nominale

Caractéristiques du débit

Modifications du schéma d'écoulement

Augmentation des turbulences: La forme aplatie crée des perturbations de l'écoulement
Perte de charge: Résistance accrue grâce aux chambres déformées
Effets d'entrée/sortie: Le positionnement des ports devient critique
Vitesse d'écoulement: Augmentation de la vitesse dans les sections restreintes

Impact du débit

Réduction de la surface d'action: Des restrictions de débit apparaissent
Pertes de charge: L'efficacité énergétique diminue
Temps de réponse: Taux de remplissage/déchargement plus lents
Performance du système: Réduction de l'efficacité globale

Considérations structurelles

Distribution des contraintes

Concentration des contraintes: Charges plus élevées dans les zones aplanies
Epaisseur du matériau: Peut nécessiter un renforcement
Résistance à la fatigue⁵: Potentiel de réduction de la durée de vie
Facteurs de sécurité: Nécessité d'augmenter les marges de conception

Effets de la pression nominale

Ratio d'aplatissement	Augmentation du stress	Facteur de sécurité recommandé	Epaisseur du matériau
0.9	10%	1.5	Standard
0.8	25%	1.8	+10%
0.7	45%	2.0	+20%
0.6	70%	2.5	+35%

Optimisation des performances du système

Stratégies de rémunération

Augmentation de la quantité d'accumulateurs: Plusieurs petites unités
Fonctionnement à plus haute pression: Compenser la perte de volume
Conception améliorée des flux: Optimiser les configurations d'entrée et de sortie
Mise au point du système: Ajuster les paramètres de contrôle

Suivi des performances

Fréquence des cycles de pression: Contrôler la stabilité du système
Mesures de débit: Vérifier que la capacité est suffisante
Effets de la température: Vérifier s'il n'y a pas d'échauffement excessif
Intervalles d'entretien: Ajuster en fonction des performances

Lignes directrices pour la conception

Sélection optimale de l'aplatissement

b/a > 0,8: Impact minimal sur les performances
b/a = 0,6-0,8: Acceptable pour la plupart des applications
b/a = 0,4-0,6: Nécessite une conception minutieuse du système
b/a < 0,4: Généralement déconseillé

Recommandations spécifiques à l'application

Cyclisme à haute fréquence: Minimiser l'aplatissement (b/a > 0,7)
Installations critiques pour l'espace: Accepter les compromis en matière de performance
Systèmes critiques de sécurité: Ratios d'aplatissement conservateurs
Projets sensibles aux coûts: Équilibre entre performance et économie d'espace

Données sur les performances dans le monde réel

Résultats de l'étude de cas

Lorsque j'ai analysé les données de performance de 50 installations avec différents taux d'aplatissement :

10% aplatissement: Impact négligeable sur les performances
30% aplatissement: 15% augmentation de la fréquence des déplacements à vélo
50% aplatissement: 40% réduction de la capacité effective
70% aplatissement: Instabilité du système dans 60% des cas

Succès de l'optimisation

Pour Elena, un intégrateur de systèmes italien, nous avons optimisé la conception de son accumulateur cylindrique sans tige en limitant l'aplatissement à b/a = 0,75, ce qui a permis de réaliser un gain d'espace de 25% tout en conservant 95% de performance du système d'origine et en éliminant les problèmes d'instabilité de la pression.

Conclusion

Le volume d'une sphère plate utilise la formule V = (4/3)πa²b avec un rayon équatorial "a" et un rayon polaire "b". L'aplatissement réduit proportionnellement le volume mais affecte la réponse à la pression et les caractéristiques d'écoulement dans les applications pneumatiques.

FAQ sur le volume d'une sphère plate

Quelle est la formule du volume d'une sphère plate ?

La formule du volume d'une sphère plate (sphéroïde oblate) est V = (4/3)πa²b, où "a" est le rayon équatorial (horizontal) et "b" le rayon polaire (vertical). Cette formule diffère de celle de la sphère parfaite V = (4/3)πr³.

Quelle est la perte de volume lors de l'aplatissement d'une sphère ?

La perte de volume est égale au taux d'aplatissement. Si le rayon polaire est égal à 70% du rayon équatorial (b/a = 0,7), le volume devient 70% du volume initial de la sphère, ce qui représente une réduction de volume de 30%.

Où sont utilisées les sphères plates dans les systèmes pneumatiques ?

Les sphères plates sont utilisées dans les chambres d'accumulateurs, les systèmes d'amortissement et les réservoirs sous pression où les restrictions de hauteur limitent les conceptions sphériques standard. Les applications courantes comprennent l'intégration de machines à l'espace restreint et les installations de modernisation.

Comment l'aplatissement affecte-t-il les performances pneumatiques ?

L'aplatissement réduit la capacité volumétrique, augmente la sensibilité à la pression et crée des turbulences dans l'écoulement. Les systèmes dont les accumulateurs sont fortement aplatis (b/a < 0,6) peuvent connaître une instabilité de la pression et une réduction de l'efficacité nécessitant une compensation au niveau de la conception.

Quel est le taux d'aplatissement maximal recommandé ?

Pour les applications pneumatiques, les rapports d'aplatissement doivent être supérieurs à b/a = 0,6 pour obtenir des performances acceptables. Les rapports inférieurs à 0,4 provoquent généralement une instabilité du système et nécessitent des modifications importantes de la conception pour maintenir un fonctionnement adéquat.

Comprendre la fonction et l'objectif des accumulateurs pneumatiques dans les systèmes d'alimentation en fluide. ↩
Apprenez la définition mathématique et les propriétés géométriques d'un sphéroïde oblat. ↩
Voir la définition officielle et les exigences de test pour l'indice de protection IP69K. ↩
Revoir les principes de la loi de Boyle, qui décrit la relation entre la pression et le volume d'un gaz. ↩
Explorer le concept de résistance à la fatigue et le comportement des matériaux sous charge cyclique. ↩

Bonjour, je suis Chuck, un expert senior avec 15 ans d'expérience dans l'industrie pneumatique. Chez Bepto Pneumatic, je me concentre sur la fourniture de solutions pneumatiques de haute qualité et sur mesure pour nos clients. Mon expertise couvre l'automatisation industrielle, la conception et l'intégration de systèmes pneumatiques, ainsi que l'application et l'optimisation de composants clés. Si vous avez des questions ou si vous souhaitez discuter des besoins de votre projet, n'hésitez pas à me contacter à l'adresse chuck@bepto.com.