L'incubo di ogni manutentore è un guasto imprevisto alle apparecchiature. Quando le macchine vibrano alla loro frequenza naturale, possono verificarsi danni catastrofici in pochi minuti. Ho visto questo problema costare alle aziende migliaia di ore di fermo macchina.
Risonanza delle vibrazioni1 si verifica quando una forza esterna corrisponde alla frequenza naturale di un sistema, causando oscillazioni amplificate che possono danneggiare le apparecchiature. La comprensione e il controllo di questo fenomeno sono essenziali per prevenire i guasti e prolungare la durata di vita dei macchinari.
Permettetemi di raccontarvi una breve storia. L'anno scorso, un cliente tedesco mi ha chiamato in preda al panico. La loro linea di produzione si era fermata perché un cilindro senza stelo vibrava violentemente. Il problema? La risonanza. Alla fine di questo articolo, capirete come identificare e prevenire problemi simili nei vostri sistemi.
Indice dei contenuti
- Formula della frequenza naturale: Come si possono calcolare i punti vulnerabili del sistema?
- Modello massa-molla: Perché questo approccio semplificato è così prezioso?
- Ottimizzazione del rapporto di smorzamento: Quali esperimenti danno i migliori risultati?
- Conclusione
- Domande frequenti sulla risonanza delle vibrazioni
Formula della frequenza naturale: Come si possono calcolare i punti vulnerabili del sistema?
Conoscere la frequenza naturale delle apparecchiature è il primo passo per prevenire i problemi di risonanza. Questo valore critico determina quando il sistema è più vulnerabile ai problemi di vibrazione.
Il frequenza naturale2 (fn) di un sistema può essere calcolata con la formula: fn = (1/2π) × √(k/m), dove k è il coefficiente di rigidità e m è la massa. Questo calcolo rivela la frequenza alla quale il sistema risuonerà se eccitato da forze esterne corrispondenti.
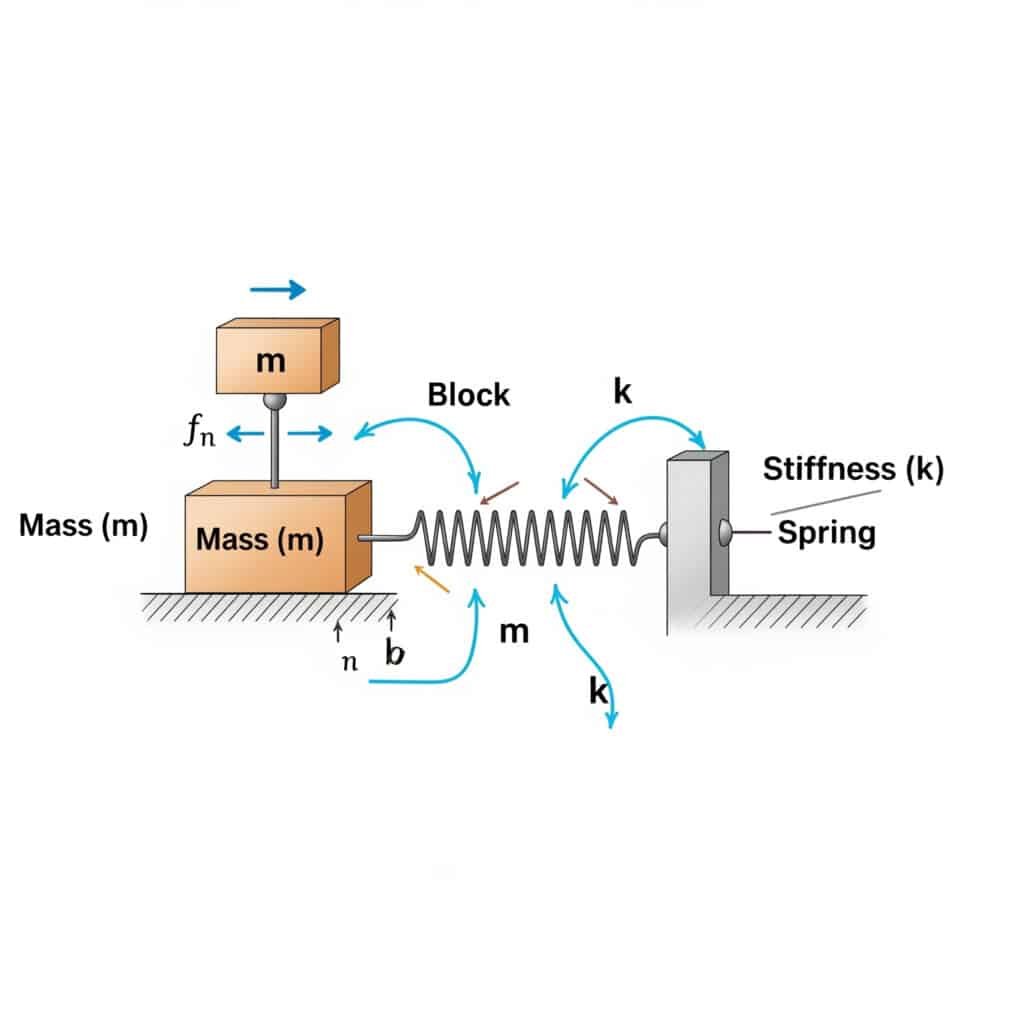
Quando ho visitato uno stabilimento di produzione in Svizzera, ho notato che i cilindri pneumatici senza stelo si guastavano prematuramente. Il team di manutenzione non aveva calcolato la frequenza naturale del sistema. Dopo aver applicato questa formula, abbiamo individuato che la velocità di funzionamento era pericolosamente vicina alla frequenza naturale del sistema.
Applicazioni pratiche del calcolo della frequenza naturale
La formula della frequenza naturale non è solo teorica: ha applicazioni dirette in vari contesti industriali:
- Selezione dell'attrezzatura: Scelta di componenti con frequenze naturali lontane dalle condizioni di funzionamento
- Manutenzione preventiva: Pianificazione delle ispezioni in base ai profili di rischio delle vibrazioni
- Risoluzione dei problemi: Identificazione della causa principale delle vibrazioni inattese
Valori di frequenza naturale comuni per i componenti industriali
| Componente | Gamma di frequenza naturale tipica (Hz) |
|---|---|
| Cilindri senza stelo | 10-50 Hz |
| Staffe di montaggio | 20-100 Hz |
| Strutture di supporto | 5-30 Hz |
| Valvole di controllo | 40-200 Hz |
Fattori critici che influenzano la frequenza naturale
Il calcolo della frequenza naturale sembra semplice, ma diversi fattori possono complicare le applicazioni reali:
- Distribuzione di massa non uniforme: La maggior parte dei componenti industriali non ha una massa perfettamente distribuita.
- Rigidità variabile: I componenti possono avere una rigidità diversa in diverse direzioni.
- Punti di connessione: Il montaggio dei componenti influisce in modo significativo sulle loro caratteristiche di vibrazione.
- Effetti della temperatura: Sia le proprietà di massa che quelle di rigidità possono cambiare con la temperatura.
Modello massa-molla: Perché questo approccio semplificato è così prezioso?
Il modello massa-molla fornisce un quadro intuitivo per la comprensione di sistemi di vibrazione complessi. Riduce i macchinari complicati a elementi di base che gli ingegneri possono facilmente analizzare.
Il modello massa-molla3 semplifica l'analisi delle vibrazioni rappresentando i sistemi meccanici come masse discrete collegate da molle. Questo approccio consente agli ingegneri di prevedere il comportamento del sistema, di identificare i potenziali problemi di risonanza e di sviluppare soluzioni efficaci senza ricorrere a complessi calcoli matematici.
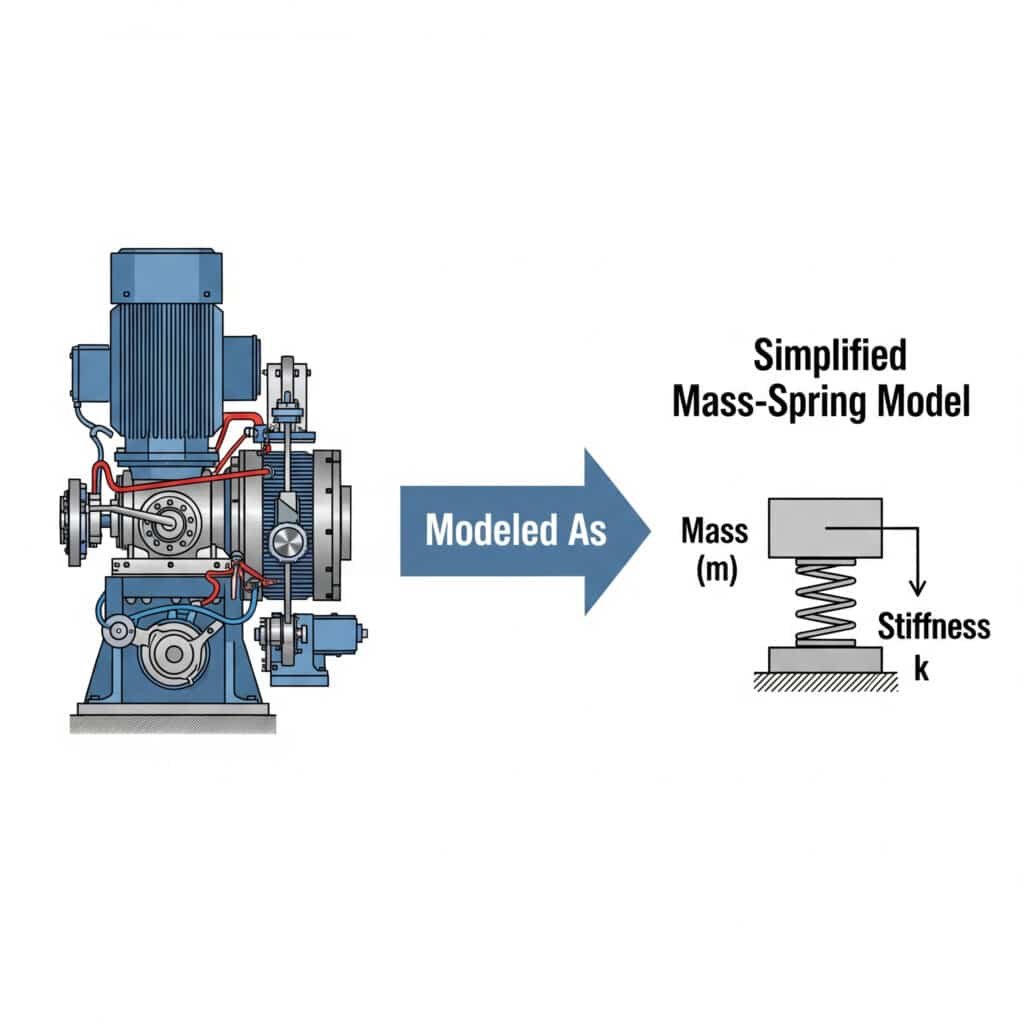
Ricordo di aver lavorato con un produttore di componenti automobilistici del Michigan che non riusciva a capire perché i suoi cilindri guidati senza stelo si guastassero. Modellando il loro sistema come una semplice disposizione massa-molla, abbiamo individuato che le staffe di montaggio agivano come molle involontarie, creando una condizione di risonanza.
Conversione di sistemi reali in modelli a molla di massa
Per applicare questo approccio alle vostre apparecchiature:
- Identificare le masse chiave: Determinare quali componenti contribuiscono in modo significativo al peso
- Individuare gli elementi a molla: Trovare componenti che immagazzinano e rilasciano energia (molle reali, supporti flessibili, ecc.).
- Collegamenti alla mappa: Documentare l'interazione tra masse e molle
- Semplificare: Combinare elementi simili per creare un modello gestibile
Tipi di sistemi di molle di massa
| Tipo di sistema | Descrizione | Applicazioni comuni |
|---|---|---|
| DOF singolo | Una massa con una molla | Cilindri pneumatici semplici |
| Multi-DOF | Masse multiple con molle multiple | Macchine complesse con più componenti |
| Continuo | DOF infinito (richiede un'analisi diversa) | Travi, piastre e gusci |
Considerazioni sulla modellazione avanzata
Sebbene il modello di base massa-molla sia valido, diversi miglioramenti lo rendono più realistico:
- Aggiunta di smorzatori: I sistemi reali hanno sempre una dissipazione di energia
- Considerare le non linearità: Le molle non sempre seguono Legge di Hooke4 perfettamente
- Contabilizzazione delle vibrazioni forzate: Le forze esterne modificano il comportamento del sistema
- Compresi gli effetti di accoppiamento: Il movimento in una direzione può influenzare altre direzioni
Ottimizzazione del rapporto di smorzamento: Quali esperimenti danno i migliori risultati?
Lo smorzamento è la migliore difesa contro i problemi di risonanza. La ricerca del rapporto di smorzamento ottimale attraverso la sperimentazione può migliorare notevolmente le prestazioni e l'affidabilità del sistema.
Rapporto di smorzamento5 Gli esperimenti di ottimizzazione prevedono il test sistematico di diverse configurazioni di smorzamento per trovare l'equilibrio ideale tra controllo delle vibrazioni e reattività del sistema. Il rapporto di smorzamento ottimale si colloca in genere tra 0,2 e 0,7, fornendo una sufficiente soppressione delle vibrazioni senza eccessive perdite di energia.
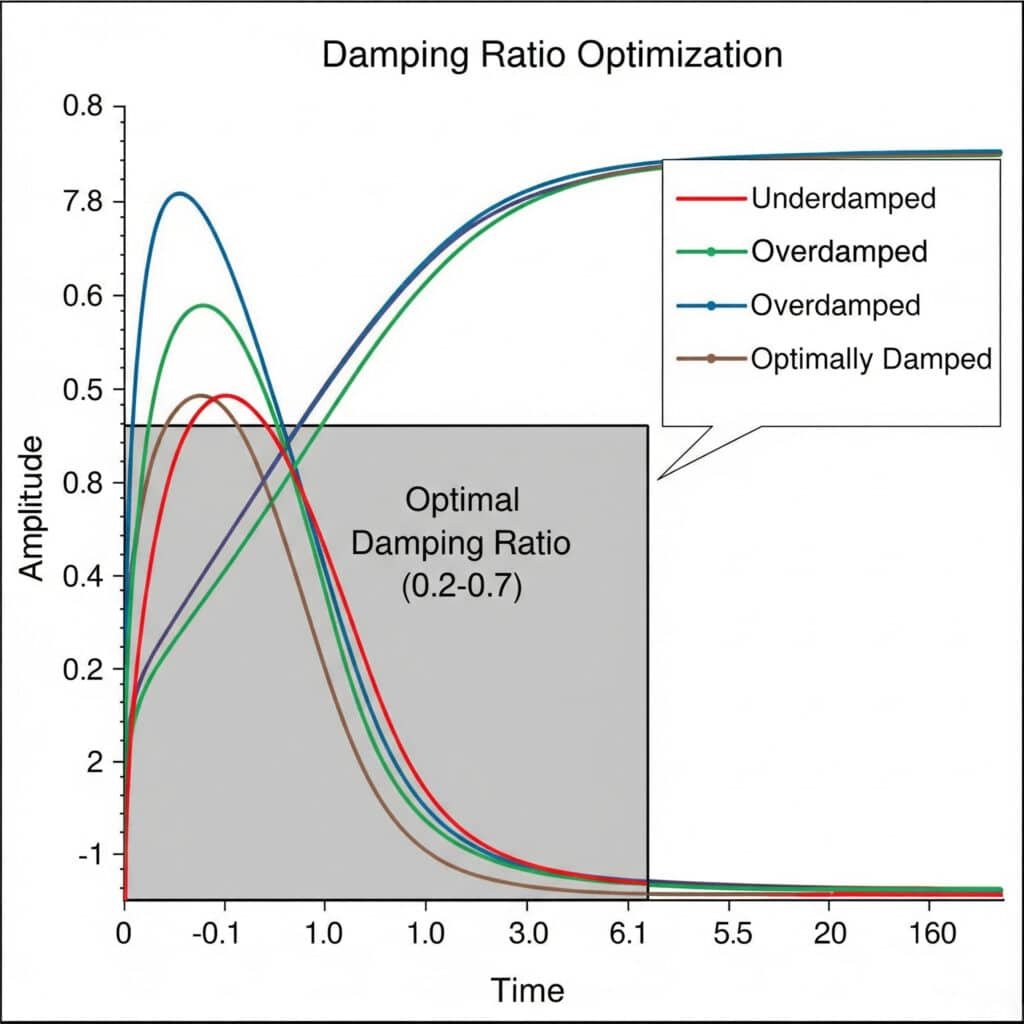
Il mese scorso ho aiutato un'azienda francese produttrice di attrezzature per la lavorazione degli alimenti a risolvere i persistenti problemi di vibrazione dei suoi cilindri magnetici senza stelo. Attraverso una serie di esperimenti sul rapporto di smorzamento, abbiamo scoperto che il loro progetto originale aveva un rapporto di smorzamento di appena 0,05, troppo basso per evitare problemi di risonanza.
Setup sperimentale per il test del rapporto di smorzamento
Per condurre esperimenti di ottimizzazione dello smorzamento efficace:
- Misurazione di base: Registrazione della risposta del sistema senza smorzamento aggiuntivo
- Test incrementali: Aggiunta di elementi di smorzamento a incrementi controllati
- Misura della risposta: Misura dell'ampiezza, del tempo di assestamento e della risposta in frequenza
- Analisi dei dati: Calcolo del rapporto di smorzamento per ogni configurazione
- Convalida: Verificare le prestazioni in condizioni operative reali
Confronto tra le tecnologie di smorzamento
| Tecnologia di smorzamento | Vantaggi | Limitazioni | Applicazioni tipiche |
|---|---|---|---|
| Ammortizzatori viscosi | Prestazioni prevedibili, temperatura stabile | Necessità di manutenzione, potenziali perdite | Macchinari pesanti, attrezzature di precisione |
| Ammortizzatori a frizione | Design semplice e conveniente | Usura nel tempo, comportamento non lineare | Supporti strutturali, macchinari di base |
| Smorzamento del materiale | Senza parti in movimento, compatto | Campo di regolazione limitato | Strumenti di precisione, isolamento dalle vibrazioni |
| Smorzamento attivo | Adattabile a condizioni mutevoli | Complesso, richiede potenza | Applicazioni critiche, apparecchiature a velocità variabile |
Ottimizzazione dello smorzamento per diverse condizioni operative
Il rapporto di smorzamento ideale non è universale: dipende dall'applicazione specifica:
- Operazioni ad alta velocità: Rapporti di smorzamento più bassi (0,1-0,3) mantengono la reattività
- Applicazioni di precisione: Rapporti di smorzamento più elevati (0,5-0,7) per una maggiore stabilità.
- Sistemi a carico variabile: Potrebbe essere necessario uno smorzamento adattativo
- Ambienti sensibili alla temperatura: Considerare materiali smorzanti con proprietà stabili
Caso di studio: Ottimizzazione dello smorzamento del cilindro senza stelo
Nell'ottimizzazione di un cilindro senza stelo a doppio effetto per una macchina per l'imballaggio, abbiamo testato cinque diverse configurazioni di smorzamento:
- Cuscini terminali standard: Rapporto di smorzamento = 0,12
- Cuscini estesi: Rapporto di smorzamento = 0,25
- Ammortizzatori esterni: Rapporto di smorzamento = 0,41
- Staffe di montaggio in materiale composito: Rapporto di smorzamento = 0,38
- Approccio combinato (3+4): Rapporto di smorzamento = 0,53
L'approccio combinato ha fornito le migliori prestazioni, riducendo l'ampiezza delle vibrazioni di 78% pur mantenendo tempi di risposta accettabili.
Conclusione
La comprensione della risonanza delle vibrazioni attraverso il calcolo della frequenza naturale, la modellazione della massa-molla e l'ottimizzazione del rapporto di smorzamento è fondamentale per prevenire i guasti alle apparecchiature. Applicando questi principi, è possibile prolungare la vita dei macchinari, ridurre i tempi di fermo e migliorare le prestazioni complessive del sistema.
Domande frequenti sulla risonanza delle vibrazioni
Che cos'è la risonanza delle vibrazioni nelle apparecchiature industriali?
La risonanza delle vibrazioni si verifica quando una forza esterna corrisponde alla frequenza naturale di un sistema, causando oscillazioni amplificate. Nelle apparecchiature industriali, questo fenomeno può portare a movimenti eccessivi, all'affaticamento dei componenti e a guasti catastrofici se non viene gestito correttamente.
Come posso identificare se il mio sistema è in risonanza?
Cercate sintomi come aumenti inspiegabili della rumorosità, vibrazioni visibili a velocità specifiche, guasti prematuri dei componenti e degrado delle prestazioni che si verificano a punti di funzionamento costanti. Gli strumenti di analisi delle vibrazioni possono confermare le condizioni di risonanza.
Qual è la differenza tra vibrazioni forzate e risonanza?
La vibrazione forzata si verifica ogni volta che una forza esterna agisce su un sistema, mentre la risonanza è la condizione specifica in cui la frequenza di forzatura coincide con la frequenza naturale del sistema, dando luogo a una risposta amplificata. Tutte le risonanze comportano vibrazioni forzate, ma non tutte le vibrazioni forzate causano risonanza.
In che modo il design di un cilindro pneumatico senza stelo influisce sulle sue caratteristiche di vibrazione?
Il design dei cilindri pneumatici senza stelo, con il loro carrello mobile, il sistema di tenuta interno e i meccanismi di guida, crea problemi di vibrazione unici. Il profilo esteso agisce come una trave che può flettersi, la massa del carrello crea forze inerziali e le bande di tenuta possono introdurre un attrito variabile.
Quali semplici modifiche possono ridurre la risonanza nelle apparecchiature esistenti?
Per le apparecchiature esistenti che presentano problemi di risonanza, considerare l'aggiunta di massa per modificare la frequenza naturale, l'installazione di smorzatori o ammortizzatori esterni, la modifica dei metodi di montaggio per includere l'isolamento dalle vibrazioni o la regolazione delle velocità operative per evitare le frequenze di risonanza.
-
Fornisce una spiegazione fondamentale della risonanza meccanica, spesso con esempi visivi, dimostrando come una piccola forza periodica possa produrre oscillazioni di grande ampiezza in un sistema. ↩
-
Offre uno sguardo dettagliato sulla fisica della frequenza naturale, la frequenza specifica alla quale un sistema tende a oscillare in assenza di forze motrici o smorzanti. ↩
-
Spiega i principi del modello massa-molla, un'idealizzazione fondamentale in fisica e ingegneria utilizzata per analizzare sistemi complessi che presentano un moto armonico semplice. ↩
-
Dettagli Legge di Hooke, un principio della fisica che afferma che la forza necessaria per estendere o comprimere una molla di una certa distanza è direttamente proporzionale a tale distanza. ↩
-
Descrive il rapporto di smorzamento, una misura adimensionale che definisce il modo in cui le oscillazioni di un sistema decadono dopo un disturbo, fondamentale per controllare la risonanza. ↩



