
Avete difficoltà a prevedere le prestazioni effettive del vostro cilindro pneumatico? Molti ingegneri calcolano erroneamente la forza erogata e i requisiti di pressione, causando guasti al sistema e costosi tempi di inattività. Ma c'è un modo semplice per padroneggiare questi calcoli.
I cilindri pneumatici funzionano in base a principi fisici fondamentali, principalmente Legge di Pascal1che afferma che la pressione applicata a un fluido confinato viene trasmessa in egual misura in tutte le direzioni. Questo ci permette di calcolare la forza del cilindro moltiplicando la pressione per l'area effettiva del pistone, con portate e unità di pressione che richiedono conversioni precise per una progettazione accurata del sistema.
Ho trascorso oltre un decennio ad aiutare i clienti a ottimizzare i loro sistemi pneumatici e ho visto come la comprensione di questi principi di base possa trasformare l'affidabilità del sistema. Permettetemi di condividere le conoscenze pratiche che vi aiuteranno a evitare gli errori comuni che vedo ogni giorno.
Indice dei contenuti
- In che modo la legge di Pascal determina la forza di uscita del cilindro?
- Qual è la relazione tra flusso d'aria e pressione nei cilindri?
- Perché la comprensione della conversione delle unità di pressione è fondamentale per la progettazione del sistema?
- Conclusione
- Domande frequenti sulla fisica nei sistemi pneumatici
In che modo la legge di Pascal determina la forza di uscita del cilindro?
La comprensione della Legge di Pascal è fondamentale per prevedere e ottimizzare le prestazioni dei cilindri in qualsiasi sistema pneumatico.
La legge di Pascal afferma che la pressione esercitata su un fluido in un sistema chiuso si trasmette in modo uguale in tutto il fluido. Per i cilindri pneumatici, ciò significa che la forza erogata è uguale alla pressione moltiplicata per l'area effettiva del pistone (F = P × A). Questa semplice relazione è alla base di tutti i calcoli della forza del cilindro.

Derivazione del calcolo della forza
Vediamo la derivazione matematica dei calcoli della forza dei cilindri:
Equazione della forza di base
L'equazione fondamentale della forza del cilindro è:
F = P × A
Dove:
- F = Forza in uscita (N)
- P = Pressione (Pa)
- A = Area effettiva del pistone (m²)
Considerazioni sull'area effettiva
L'area effettiva varia a seconda del tipo di cilindro e della direzione:
| Tipo di cilindro | Forza di estensione | Forza di ritrazione |
|---|---|---|
| A singolo effetto | P × A | Solo forza della molla |
| A doppio effetto (standard) | P × A | P × (A - a) |
| A doppio effetto (senza stelo) | P × A | P × A |
Dove:
- A = Area completa del pistone
- a = Area della sezione trasversale dell'asta
Una volta mi sono consultato con uno stabilimento di produzione dell'Ohio che aveva riscontrato una forza insufficiente nella sua applicazione di pressatura. I loro calcoli sembravano corretti sulla carta, ma le prestazioni effettive erano insufficienti. Dopo aver indagato, ho scoperto che stavano usando pressione manometrica2 nei loro calcoli invece della pressione assoluta, e non avevano tenuto conto dell'area dell'asta durante la ritrazione. Dopo aver ricalcolato con la formula e i valori di pressione corretti, siamo stati in grado di dimensionare correttamente il loro sistema, aumentando la produttività di 23%.
Esempi pratici di calcolo della forza
Esaminiamo alcuni calcoli del mondo reale:
Esempio 1: forza di estensione in un cilindro standard
Per un cilindro con:
- Diametro del foro = 50 mm (raggio = 25 mm = 0,025 m)
- Pressione di esercizio = 6 bar (600.000 Pa)
L'area del pistone è:
A = π × r² = π × (0,025)² = 0,001963 m²
La forza di estensione è:
F = P × A = 600.000 Pa × 0,001963 m² = 1.178 N ≈ 118 kg forza
Esempio 2: Forza di ritrazione nello stesso cilindro
Se il diametro dell'asta è di 20 mm (raggio = 10 mm = 0,01 m):
L'area dell'asta è:
a = π × r² = π × (0,01)² = 0,000314 m²
L'area di ritrazione effettiva è:
A - a = 0,001963 - 0,000314 = 0,001649 m²
La forza di ritrazione è:
F = P × (A - a) = 600.000 Pa × 0,001649 m² = 989 N ≈ 99 kg forza
Fattori di efficienza nelle applicazioni del mondo reale
Nelle applicazioni pratiche, diversi fattori influenzano il calcolo teorico della forza:
Perdite per attrito
L'attrito tra la guarnizione del pistone e la parete del cilindro riduce la forza effettiva:
| Tipo di guarnizione | Fattore di efficienza tipico |
|---|---|
| NBR standard | 0.85-0.90 |
| PTFE a basso attrito | 0.90-0.95 |
| Guarnizioni invecchiate/usurate | 0.70-0.85 |
Equazione pratica della forza
L'equazione della forza reale è più accurata:
F_attuale = η × P × A
Dove:
- η (eta) = fattore di efficienza (in genere 0,85-0,95)
Qual è la relazione tra flusso d'aria e pressione nei cilindri?
La comprensione della relazione tra portata e pressione è fondamentale per il dimensionamento dei sistemi di alimentazione dell'aria e per la previsione della velocità dei cilindri.
La portata e la pressione dell'aria nei sistemi pneumatici sono inversamente correlate: quando la pressione aumenta, la portata tipicamente diminuisce. Questa relazione segue le leggi dei gas ed è influenzata da restrizioni, temperatura e volume del sistema. Il corretto funzionamento del cilindro richiede il bilanciamento di questi fattori per ottenere la velocità e la forza desiderate.
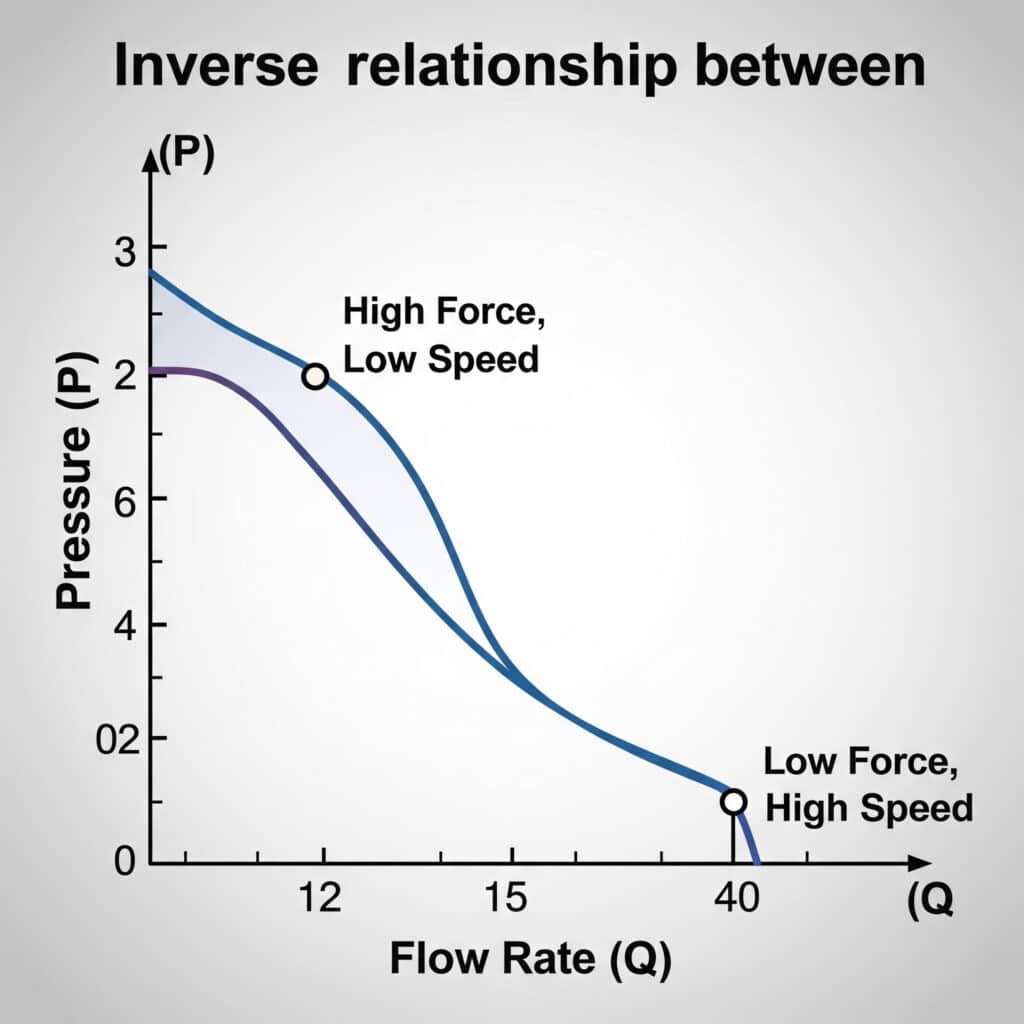
Tabella di conversione flusso-pressione
Questa pratica tabella di riferimento mostra la relazione tra la portata e la caduta di pressione nei vari componenti del sistema:
| Dimensioni del tubo (mm) | Portata (l/min) | Perdita di carico (bar/metro) a 6 bar di alimentazione |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
La matematica del flusso e della pressione
La relazione tra flusso e pressione segue diverse leggi dei gas:
Equazione di Poiseuille3 per il flusso laminare
Per il flusso laminare attraverso i tubi:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Dove:
- Q = Portata volumetrica
- r = raggio del tubo
- ΔP = differenza di pressione
- η = viscosità dinamica
- L = Lunghezza del tubo
Coefficiente di flusso (Cv)4 Metodo
Per componenti come le valvole:
Q = Cv × √ΔP
Dove:
- Q = Portata
- Cv = Coefficiente di flusso
- ΔP = caduta di pressione attraverso il componente
Calcolo della velocità del cilindro
La velocità di un cilindro pneumatico dipende dalla portata e dall'area del cilindro:
v = Q / A
Dove:
- v = Velocità del cilindro (m/s)
- Q = Portata (m³/s)
- A = Area del pistone (m²)
Durante un recente progetto presso un impianto di confezionamento in Francia, mi sono imbattuto in una situazione in cui i cilindri senza stelo del cliente si muovevano troppo lentamente nonostante una pressione adeguata. Analizzando il loro sistema con i nostri calcoli di portata e pressione, abbiamo identificato le linee di alimentazione sottodimensionate che causavano una significativa caduta di pressione. Dopo il passaggio da tubi da 6 mm a 10 mm, il tempo di ciclo è migliorato di 40%, aumentando notevolmente la capacità produttiva.
Considerazioni critiche sul flusso
Diversi fattori influenzano la relazione flusso-pressione nei sistemi pneumatici:
Fenomeno del flusso strozzato5
Quando il rapporto di pressione supera un valore critico (circa 0,53 per l'aria), il flusso diventa "strozzato" e non può aumentare indipendentemente dalla riduzione della pressione a valle.
Effetti della temperatura
La portata è influenzata dalla temperatura secondo la relazione:
Q₂ = Q₁ × √(T₂/T₁)
Dove:
- Q₁, Q₂ = Portate a diverse temperature
- T₁, T₂ = temperature assolute
Perché la comprensione della conversione delle unità di pressione è fondamentale per la progettazione del sistema?
La navigazione tra le varie unità di pressione utilizzate in tutto il mondo è essenziale per una corretta progettazione del sistema e per la compatibilità internazionale.
La conversione delle unità di pressione è fondamentale perché i componenti pneumatici e le specifiche utilizzano unità diverse a seconda della regione e del settore. Un'interpretazione errata delle unità può portare a errori di calcolo significativi, con conseguenze potenzialmente pericolose. La conversione tra pressione assoluta, relativa e differenziale aggiunge un ulteriore livello di complessità.
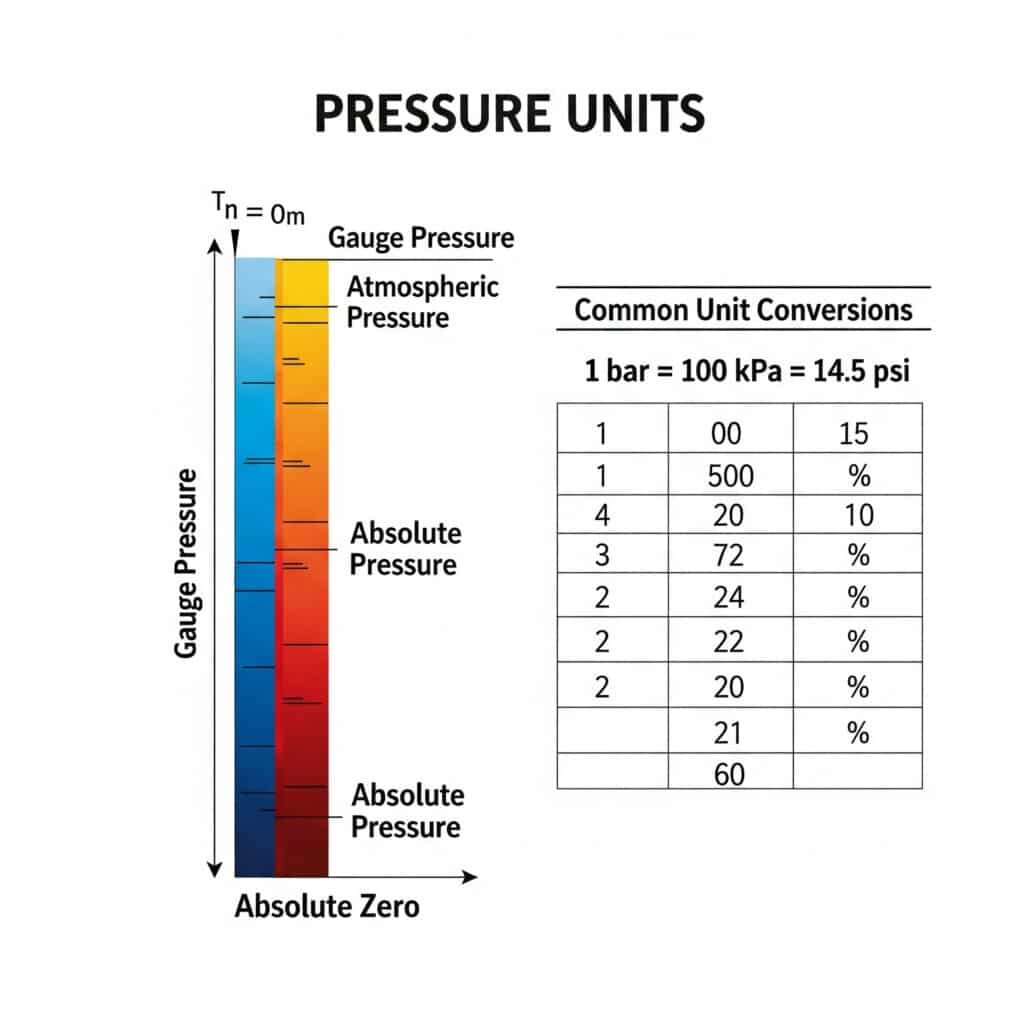
Guida alla conversione delle unità di misura della pressione assoluta
Questa tabella di conversione completa aiuta a orientarsi tra le varie unità di pressione utilizzate a livello globale:
| Unità | Simbolo | Equivalente in Pa | Equivalente in bar | Equivalente in psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bar | 1 × 10⁵ | 1 | 14.5038 |
| Libbra per pollice quadrato | psi | 6,894.76 | 0.0689476 | 1 |
| Chilogrammo-forza per cm quadrato | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmosfera | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Millimetro di mercurio | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Pollici d'acqua | inH₂O | 249.089 | 0.00249089 | 0.0361274 |
Pressione assoluta e pressione relativa
È fondamentale capire la differenza tra pressione assoluta e relativa:
Calcolatore di conversione della pressione
Convertitore di unità di pressione
Convertitore di portata del cilindro
Formule di conversione
- P_assoluta = P_gomma + P_atmosferica
- P_gamma = P_assoluta - P_atmosferica
Dove la pressione atmosferica standard è approssimativamente:
- 1,01325 bar
- 14,7 psi
- 101.325 Pa
Una volta ho lavorato con un team di ingegneri in Germania che aveva acquistato i nostri cilindri senza stelo, ma aveva segnalato che non raggiungevano la forza prevista. Dopo un po' di ricerche, abbiamo scoperto che stavano usando le nostre tabelle di forza (che si basavano sulla pressione relativa) ma inserendo valori di pressione assoluta. Questo semplice malinteso causava un errore di calcolo di 1 bar nelle loro aspettative di forza. Dopo aver chiarito il riferimento alla pressione, il sistema ha funzionato esattamente come specificato.
Esempi pratici di conversione
Vediamo alcuni scenari di conversione comuni:
Esempio 1: Conversione della pressione di esercizio tra le unità di misura
Un cilindro con pressione massima di esercizio di 0,7 MPa:
Nel bar:
0,7 MPa × 10 bar/MPa = 7 bar
In psi:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Esempio 2: conversione da pressione relativa a pressione assoluta
Un sistema funzionante a 6 bar di pressione relativa:
In pressione assoluta (bar):
6 bar_gauge + 1,01325 bar_atmosferici = 7,01325 bar_assoluti
Esempio 3: Conversione da kgf/cm² a MPa
Un cilindro giapponese specificato per 7 kgf/cm²:
In MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Preferenze delle unità di pressione regionali
Le diverse regioni utilizzano in genere unità di pressione diverse:
| Regione | Unità di pressione comuni |
|---|---|
| Nord America | psi, inHg, inH₂O |
| Europa | bar, Pa, mbar |
| Giappone | kgf/cm², MPa |
| Cina | MPa, bar |
| REGNO UNITO | bar, psi, Pa |
Misura della pressione nella documentazione
Quando si documentano le specifiche di pressione, è essenziale indicare chiaramente:
- Il valore numerico
- L'unità di misura
- Che si tratti di pressione relativa (g) o assoluta (a)
Ad esempio:
- 6 bar_g (pressione relativa, 6 bar sopra l'atmosfera)
- 7,01 bar_a (pressione assoluta, pressione totale inclusa quella atmosferica)
Conclusione
La comprensione della fisica alla base dei cilindri pneumatici, dai calcoli della forza della Legge di Pascal alle relazioni flusso-pressione e alle conversioni delle unità di pressione, è essenziale per una corretta progettazione del sistema e per la risoluzione dei problemi. Questi principi fondamentali aiutano a garantire che i sistemi pneumatici forniscano le prestazioni previste in modo affidabile ed efficiente.
Domande frequenti sulla fisica nei sistemi pneumatici
Come si calcola la forza in uscita di un cilindro pneumatico senza stelo?
Per calcolare la forza erogata da un cilindro pneumatico senza stelo, moltiplicare la pressione di esercizio per l'area effettiva del pistone (F = P × A). Ad esempio, un cilindro senza stelo con un alesaggio di 50 mm (area di 0,001963 m²) funzionante a 6 bar (600.000 Pa) produrrà circa 1.178 N di forza. A differenza dei cilindri tradizionali, i cilindri senza stelo hanno in genere la stessa area effettiva in entrambe le direzioni.
Come si calcola la forza in uscita di un cilindro pneumatico senza stelo?
Per calcolare la forza erogata da un cilindro pneumatico senza stelo, moltiplicare la pressione di esercizio per l'area effettiva del pistone (F = P × A). Ad esempio, un cilindro senza stelo con un alesaggio di 50 mm (area di 0,001963 m²) funzionante a 6 bar (600.000 Pa) produrrà circa 1.178 N di forza. A differenza dei cilindri tradizionali, i cilindri senza stelo hanno in genere la stessa area effettiva in entrambe le direzioni.
Qual è la differenza tra pressione relativa e pressione assoluta?
La pressione relativa (bar_g, psi_g) misura la pressione rispetto alla pressione atmosferica, che è pari a zero. La pressione assoluta (bar_a, psi_a) misura la pressione rispetto al vuoto perfetto, che è pari a zero. Per passare dalla pressione relativa a quella assoluta, aggiungere la pressione atmosferica (circa 1,01325 bar o 14,7 psi) alla lettura del manometro.
In che modo il flusso d'aria influisce sulla velocità del cilindro?
La velocità del cilindro è direttamente proporzionale alla portata d'aria e inversamente proporzionale all'area del pistone (v = Q/A). Una portata insufficiente dovuta a linee di alimentazione sottodimensionate, raccordi restrittivi o valvole inadeguate limita la velocità del cilindro indipendentemente dalla pressione. Ad esempio, una portata di 20 litri/secondo attraverso un cilindro con un'area del pistone di 0,002 m² produrrà una velocità di 10 metri/secondo.
Perché i cilindri pneumatici a volte si muovono più lentamente di quanto calcolato?
I cilindri pneumatici possono muoversi più lentamente di quanto calcolato a causa di diversi fattori: restrizioni nell'alimentazione dell'aria che causano perdite di pressione, attrito interno delle guarnizioni, carichi meccanici superiori ai calcoli, perdite che riducono la pressione effettiva o effetti della temperatura sulla densità dell'aria. Inoltre, i coefficienti di flusso delle valvole spesso limitano la portata effettiva disponibile per il cilindro.
Come si fa a convertire le diverse unità di pressione per le specifiche internazionali?
Per convertire le unità di pressione, utilizzare i fattori di moltiplicazione: 1 bar = 100.000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Verificare sempre se la pressione è specificata come relativa o assoluta, poiché questa distinzione può influenzare notevolmente i calcoli. Ad esempio, 6 bar_g equivalgono a 7,01325 bar_a in condizioni atmosferiche standard.
Qual è la relazione tra le dimensioni dell'alesaggio del cilindro e la forza erogata?
La relazione tra le dimensioni dell'alesaggio del cilindro e la forza erogata è quadratica: raddoppiando il diametro dell'alesaggio, la forza erogata aumenta di quattro volte (poiché l'area = π × r²). Ad esempio, a una pressione di esercizio di 6 bar, un cilindro con alesaggio di 40 mm produce una forza di circa 754 N, mentre un cilindro con alesaggio di 80 mm produce circa 3.016 N, quasi quattro volte di più.
-
Fornisce una spiegazione dettagliata della Legge di Pascal, un principio fondamentale della meccanica dei fluidi che è alla base della trasmissione di potenza idraulica e pneumatica. ↩
-
Offre una chiara definizione e un confronto tra pressione relativa e assoluta, una distinzione fondamentale per calcoli ingegneristici accurati, poiché la pressione relativa è relativa alla pressione atmosferica. ↩
-
Spiega la derivazione e l'applicazione della legge di Poiseuille, che descrive la caduta di pressione di un fluido incomprimibile e newtoniano che scorre in un lungo tubo cilindrico in regime laminare. ↩
-
Fornisce una definizione tecnica del coefficiente di flusso (Cv), una misura imperiale che fornisce un metodo standardizzato per confrontare le capacità di flusso di diverse valvole. ↩
-
Dettagli sulla fisica del flusso strozzato, una condizione fluidodinamica che limita la portata massica di un fluido comprimibile attraverso una restrizione quando la velocità raggiunge la velocità del suono. ↩


