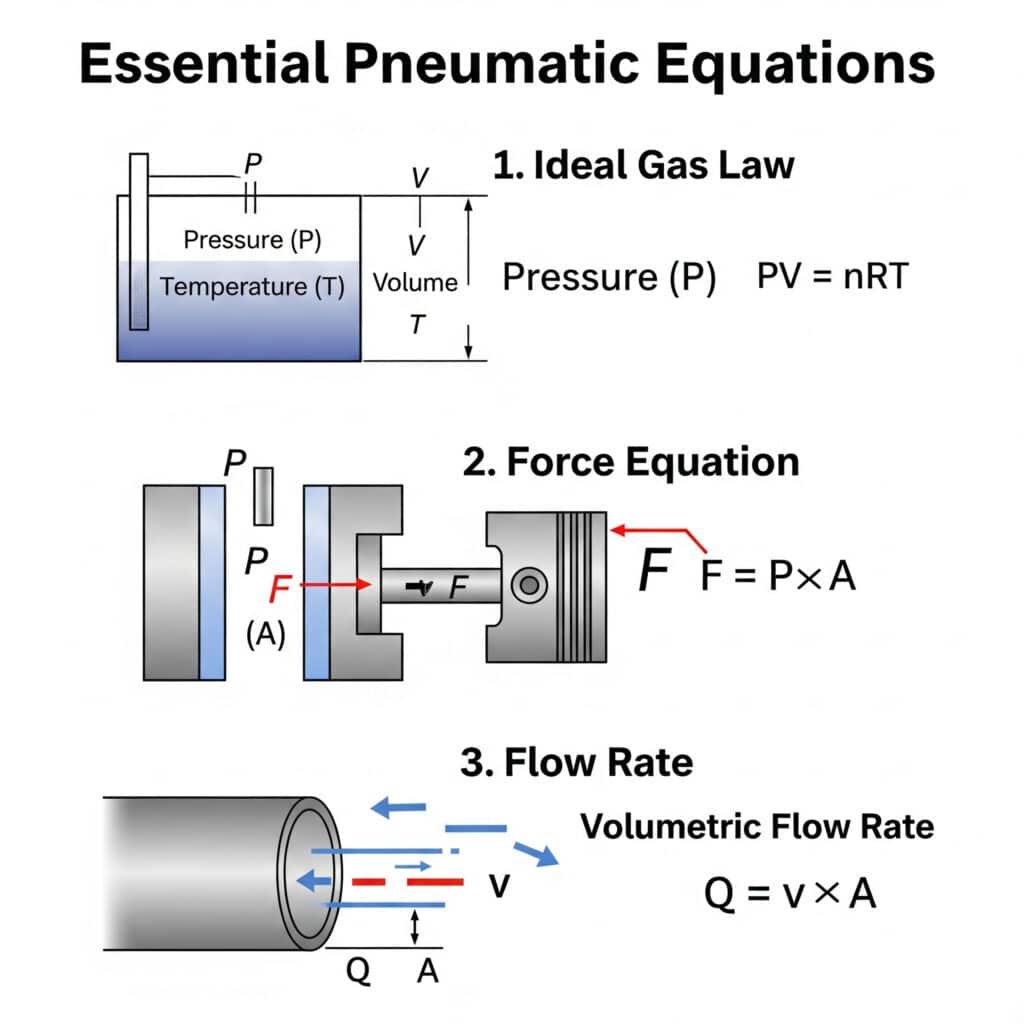
Siete sempre alle prese con i calcoli dei sistemi pneumatici? Molti ingegneri si trovano ad affrontare lo stesso problema quando progettano o risolvono i problemi dei sistemi pneumatici. La buona notizia è che la padronanza di alcune equazioni chiave può risolvere la maggior parte delle vostre sfide pneumatiche.
Le equazioni essenziali per la trasmissione pneumatica che ogni ingegnere dovrebbe conoscere sono le seguenti legge dei gas ideali (PV = nRT)1L'equazione della forza (F = P × A) e la relazione di portata (Q = v × A). La comprensione di questi fondamenti consente una progettazione accurata del sistema e la risoluzione dei problemi.
Ho lavorato per oltre 15 anni con i sistemi pneumatici alla Bepto e ho visto di persona come la comprensione di queste equazioni di base possa far risparmiare migliaia di dollari in tempi di inattività e prevenire costosi errori di progettazione.
Indice dei contenuti
- Derivazione dell'equazione dei gas: Perché PV = nRT è importante nei sistemi pneumatici?
- Qual è il rapporto tra forza, pressione e area nei cilindri pneumatici?
- Qual è la relazione tra portata e velocità nei sistemi pneumatici?
- Conclusione
- Domande frequenti sulle equazioni della trasmissione pneumatica
Derivazione dell'equazione dei gas: Perché PV = nRT è importante nei sistemi pneumatici?
Quando si progettano sistemi pneumatici, è fondamentale capire come si comportano i gas in diverse condizioni. Questa conoscenza può fare la differenza tra un sistema che funziona in modo affidabile e uno che si guasta inaspettatamente.
La legge dei gas ideali (PV = nRT) è fondamentale per i sistemi pneumatici perché descrive l'interazione tra pressione, volume e temperatura. Questa relazione aiuta gli ingegneri a prevedere il comportamento dell'aria nei cilindri senza stelo e in altri componenti pneumatici in condizioni operative diverse.

La legge dei gas ideali può sembrare un concetto teorico da lezione di fisica, ma ha applicazioni pratiche dirette nei sistemi pneumatici. Permettetemi di spiegarla in termini più pratici.
Comprensione delle variabili in PV = nRT
| Variabile | Significato | Applicazione pneumatica |
|---|---|---|
| P | Pressione | Pressione di esercizio del sistema |
| V | Volume | Dimensioni della camera d'aria in cilindri |
| n | Numero di moli | Quantità di aria nel sistema |
| R | Costante del gas2 | Costante universale (8,314 J/mol-K) |
| T | Temperatura | Temperatura di esercizio |
Come la temperatura influisce sulle prestazioni pneumatiche
Le variazioni di temperatura possono avere un impatto significativo sulle prestazioni dei sistemi pneumatici. L'anno scorso, uno dei nostri clienti in Germania, Hans, mi ha contattato per le prestazioni incoerenti del suo sistema di cilindri senza stelo. Il sistema funzionava perfettamente al mattino, ma perdeva potenza nel pomeriggio.
Dopo aver analizzato la sua configurazione, abbiamo scoperto che il sistema era esposto alla luce diretta del sole, causando un aumento della temperatura di 15°C. Utilizzando la legge dei gas ideali, abbiamo calcolato che questa variazione di temperatura causava una variazione di pressione di quasi 5%. Abbiamo installato un isolamento adeguato e il problema è stato risolto immediatamente.
Applicazioni pratiche della legge dei gas nella progettazione pneumatica
Quando si progettano sistemi pneumatici con cilindri senza steloLa legge dei gas ci aiuta:
- Calcolo delle variazioni di pressione dovute alle fluttuazioni di temperatura
- Determinare i requisiti di volume per i serbatoi d'aria.
- Prevedere le variazioni di forza in uscita in diverse condizioni
- Dimensionare i compressori in modo adeguato all'applicazione
Qual è il rapporto tra forza, pressione e area nei cilindri pneumatici?
La comprensione della relazione tra forza, pressione e area è essenziale per la scelta del cilindro senza stelo più adatto alla vostra applicazione. Questa conoscenza vi assicura le prestazioni necessarie senza dover spendere troppo.
Il relazione forza-pressione-area3 nei cilindri pneumatici è definita da F = P × A, dove F è la forza (N), P la pressione (Pa) e A l'area effettiva (m²). Questa equazione consente agli ingegneri di calcolare l'esatta forza erogata dai cilindri senza stelo a diverse pressioni di esercizio.
Questa semplice equazione è alla base di tutti i calcoli della forza pneumatica, ma ci sono diverse considerazioni pratiche che molti ingegneri trascurano.
Calcoli dell'area effettiva per diversi tipi di cilindri
L'area effettiva varia a seconda del tipo di cilindro:
| Tipo di cilindro | Calcolo dell'area effettiva | Note |
|---|---|---|
| A singolo effetto | A = πr² | Area del foro completo |
| A doppio effetto (estensione) | A = πr² | Area del foro completo |
| A doppio effetto (ritrazione) | A = π(r² - r'²) | r' è il raggio dell'asta |
| Cilindro senza stelo | A = πr² | Coerente in entrambe le direzioni |
Fattori di efficienza della forza nel mondo reale
In pratica, la forza effettiva erogata è influenzata da:
- Perdite per attrito: In genere 3-20% a seconda del tipo di tenuta.
- Gocce di pressione: Può ridurre la pressione effettiva di 5-10%
- Effetti dinamici: Le forze di accelerazione possono ridurre la forza disponibile
Ricordo di aver lavorato con Sarah, un ingegnere meccanico di un'azienda di packaging del Regno Unito. Stava progettando una nuova macchina e aveva calcolato che era necessario un cilindro senza stelo con un alesaggio di 63 mm per ottenere la forza richiesta. Tuttavia, non aveva tenuto conto delle perdite per attrito.
Abbiamo consigliato di passare a un cilindro con alesaggio di 80 mm, che ha fornito una forza aggiuntiva sufficiente a superare l'attrito, mantenendo le prestazioni richieste. Questa semplice regolazione le ha evitato una costosa riprogettazione dopo l'installazione.
Confronto tra forza teorica e reale
Per la scelta dei cilindri senza stelo, consiglio sempre:
- Calcolare la forza teorica utilizzando F = P × A
- Applicare un fattore di sicurezza di 25% per la maggior parte delle applicazioni.
- Verificare i calcoli con i dati di prestazione effettivi forniti dal produttore.
- Considerare le condizioni di carico dinamico, se applicabile
Qual è la relazione tra portata e velocità nei sistemi pneumatici?
La portata e la velocità sono parametri critici che determinano la velocità di risposta del sistema pneumatico. La comprensione di questa relazione aiuta a prevenire prestazioni lente e a garantire che il sistema soddisfi i requisiti di tempo di ciclo.
La relazione tra portata (Q) e velocità (v)4 nei sistemi pneumatici è definita da Q = v × A, dove Q è la portata volumetrica, v è la velocità dell'aria e A è l'area della sezione trasversale del passaggio. Questa equazione è fondamentale per dimensionare correttamente le linee d'aria e le valvole.
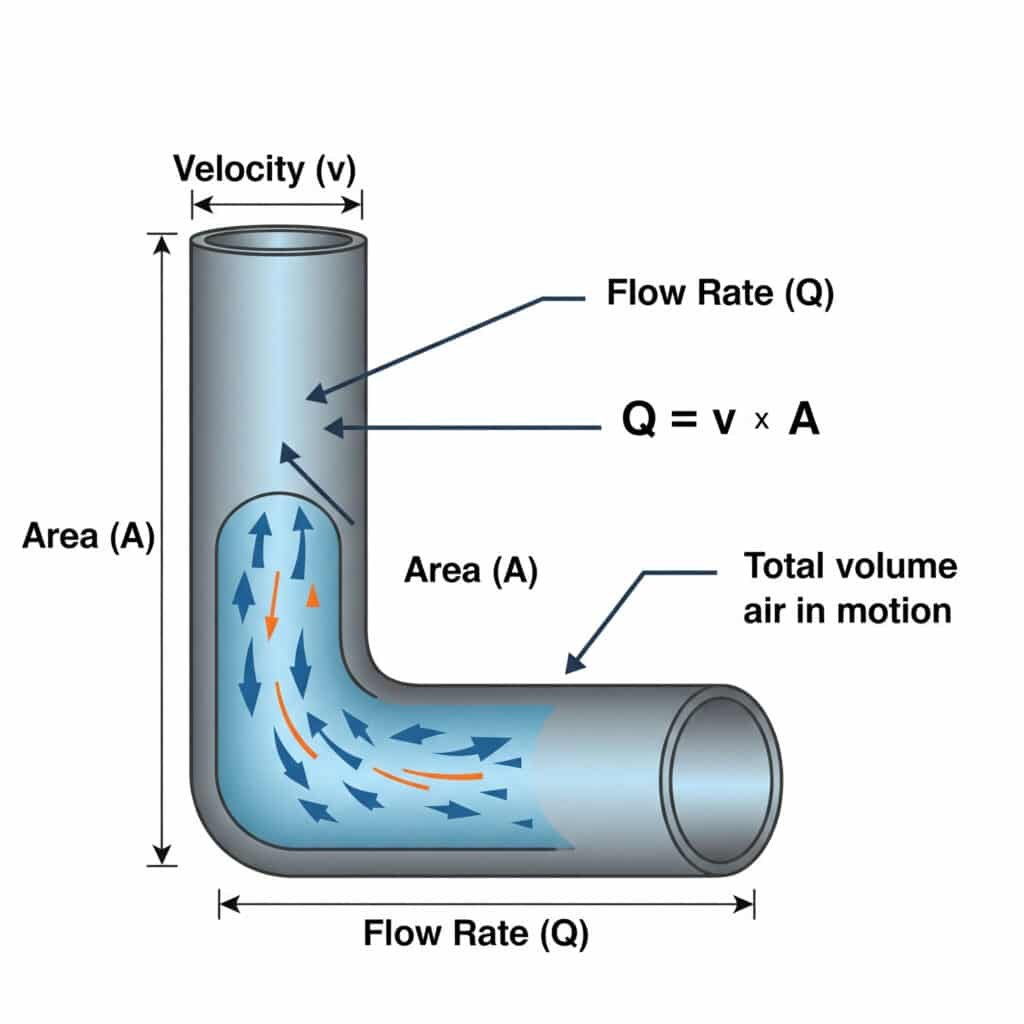
Molti problemi dei sistemi pneumatici derivano da un dimensionamento errato dei componenti di alimentazione dell'aria. Vediamo come questa equazione influisce sulle prestazioni reali.
Portate critiche per i comuni componenti pneumatici
I diversi componenti hanno requisiti di flusso diversi:
| Componente | Portata tipica richiesta | Impatto del sottodimensionamento |
|---|---|---|
| Cilindro senza stelo (alesaggio 25 mm) | 15-30 L/min | Funzionamento lento, forza ridotta |
| Cilindro senza stelo (alesaggio 63 mm) | 60-120 L/min | Movimento incoerente |
| Valvola di controllo direzionale | Varia in base alle dimensioni | Caduta di pressione, risposta lenta |
| Unità di preparazione dell'aria | Totale del sistema + 30% | Fluttuazioni di pressione |
Come il diametro dei tubi influisce sulle prestazioni del sistema
Il diametro dei tubi dell'aria ha un effetto notevole sulle prestazioni del sistema:
- Caduta di pressione: Aumenta con il quadrato della velocità
- Tempo di risposta: Linee più piccole significano maggiore velocità, ma maggiore resistenza.
- Efficienza energetica: Linee più grandi riducono la caduta di pressione ma aumentano i costi
Calcolo delle dimensioni corrette delle linee per i sistemi pneumatici
Per dimensionare correttamente le linee dell'aria per l'applicazione del cilindro senza stelo:
- Determinare la portata richiesta in base alle dimensioni del cilindro e al tempo di ciclo
- Calcolare la caduta di pressione massima consentita (in genere 0,1 bar o meno).
- Selezionare un diametro di linea che mantenga la velocità al di sotto di 15-20 m/s.
- Verificare la capacità di flusso della valvola (Valore Cv o Kv5) corrisponde ai requisiti di sistema
Una volta ho aiutato un cliente in Francia che aveva un movimento lento del cilindro nonostante avesse un compressore di grandi dimensioni. Il problema non era una generazione d'aria insufficiente, ma la sua tubazione da 6 mm creava una resistenza eccessiva. L'aggiornamento a tubi da 10 mm ha risolto immediatamente il problema, aumentando la velocità di ciclo della macchina di 40%.
Conclusione
La comprensione di queste tre equazioni pneumatiche fondamentali - la legge dei gas ideali, la relazione forza-pressione-area e la connessione portata-velocità - fornisce le basi per una progettazione efficace dei sistemi pneumatici. Applicando questi principi, è possibile scegliere i componenti giusti del cilindro senza stelo, risolvere efficacemente i problemi e ottimizzare le prestazioni del sistema.
Domande frequenti sulle equazioni della trasmissione pneumatica
Che cos'è la legge dei gas ideali e perché è importante per i sistemi pneumatici?
La legge dei gas ideali (PV = nRT) descrive il rapporto tra pressione, volume, temperatura e quantità di gas in un sistema pneumatico. È importante perché aiuta gli ingegneri a prevedere come le condizioni variabili (in particolare la temperatura) influiranno sulle prestazioni del sistema e sui requisiti di pressione.
Come si calcola la forza in uscita di un cilindro senza stelo?
Calcolare la forza in uscita moltiplicando la pressione per l'area effettiva (F = P × A). Per un cilindro senza stelo, l'area effettiva è la stessa in entrambe le direzioni, rendendo i calcoli della forza più semplici rispetto ai cilindri convenzionali che hanno forze di estensione e retrazione diverse.
Qual è la differenza tra portata e velocità nei sistemi pneumatici?
La portata è il volume d'aria che si muove attraverso un sistema per unità di tempo (tipicamente in L/min), mentre la velocità è la velocità con cui l'aria si muove attraverso un passaggio (in m/s). Sono correlate dall'equazione Q = v × A, dove A è l'area della sezione trasversale del passaggio.
In che modo la temperatura influisce sulle prestazioni del sistema pneumatico?
La temperatura influisce direttamente sulla pressione secondo la legge dei gas ideali. Un aumento di 10°C della temperatura può aumentare la pressione di circa 3,5% se il volume rimane costante. Ciò può causare variazioni di pressione, influire sulle prestazioni della tenuta e modificare la forza erogata nei cilindri senza stelo.
Qual è la causa più comune di caduta di pressione nei sistemi pneumatici?
Le cause più comuni di caduta di pressione sono linee d'aria sottodimensionate, raccordi restrittivi e capacità di flusso della valvola inadeguata. Secondo l'equazione della portata, passaggi più piccoli richiedono una maggiore velocità dell'aria, che aumenta esponenzialmente la resistenza e la caduta di pressione.
Come si dimensionano correttamente i tubi dell'aria per un cilindro senza stelo?
Dimensionare le linee d'aria calcolando la portata necessaria in base al volume del cilindro e al tempo di ciclo, quindi selezionare un diametro della linea che mantenga la velocità dell'aria al di sotto di 15-20 m/s per ridurre al minimo la caduta di pressione. Per la maggior parte delle applicazioni con cilindri senza stelo, le linee da 8-12 mm offrono un buon equilibrio tra prestazioni e costi.
-
Fornisce una spiegazione dettagliata della legge dei gas ideali, l'equazione di stato fondamentale per un ipotetico gas ideale che approssima il comportamento di molti gas in varie condizioni. ↩
-
Spiega il ruolo e il valore della costante universale dei gas (R) nella legge dei gas ideali, che funge da costante fisica che collega le scale dell'energia con quelle della temperatura. ↩
-
Offre una spiegazione fondamentale della pressione, definita come la forza applicata perpendicolarmente alla superficie di un oggetto per unità di superficie su cui tale forza è distribuita. ↩
-
Illustra il principio dell'equazione di continuità, un concetto fondamentale della dinamica dei fluidi secondo il quale, per un fluido incomprimibile, la portata di massa deve essere costante da una sezione trasversale di un tubo all'altra. ↩
-
Fornisce una definizione tecnica del coefficiente di flusso (Cv) e del fattore di flusso (Kv), che sono valori standardizzati utilizzati per confrontare le capacità di flusso di diverse valvole. ↩



