空気圧技術の基本理論とは何か、そしてそれは産業オートメーションをどのように変革するのか？

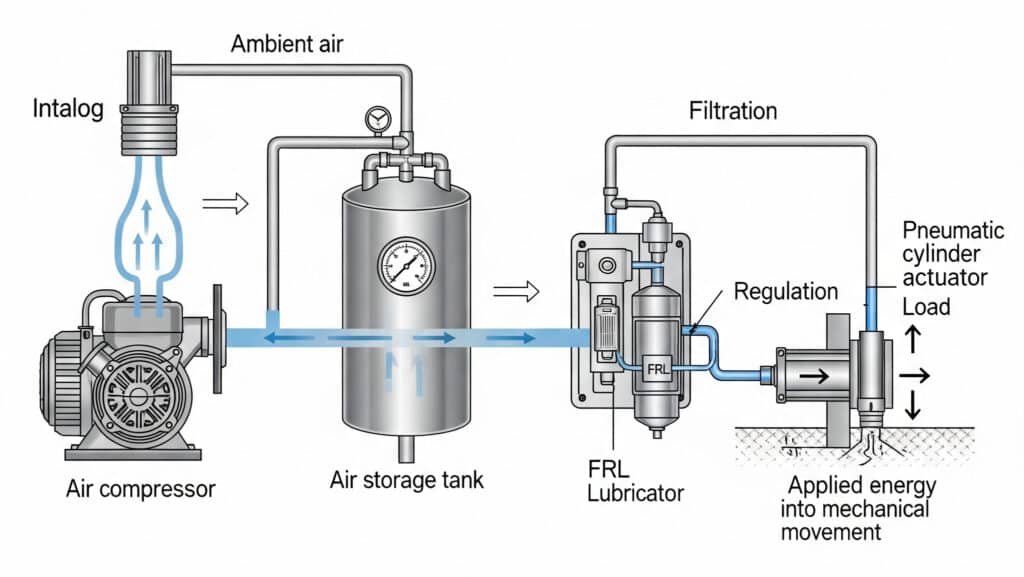
空気圧理論の誤解は、非効率な設計とシステム故障により、メーカーに年間300億ドル以上の損失をもたらしている。エンジニアは空気圧システムを単純化された油圧システムとして扱い、空気の基本的な挙動原理を無視しがちだ。空気圧理論を理解することで、致命的な設計ミスを防ぎ、システムの最適化可能性を引き出せる。.

空気圧理論は圧縮空気エネルギー変換に基づくもので、大気中の空気を圧縮して位置エネルギーを蓄積し、配管システムを通じて伝達され、アクチュエータを介して機械的仕事に変換される。これは以下の要素によって制御される。 熱力学の原理¹ および流体力学。.

6か月前、私はエリック・リンドクヴィストというスウェーデンの自動化エンジニアと協力した。彼の工場の空気圧システムは設計値より40%多くのエネルギーを消費していた。彼のチームは空気圧理論の基礎を理解せずに基本的な圧力計算を適用していた。適切な空気圧理論の原則を導入した結果、エネルギー消費量を45%削減すると同時に、システム性能を60%向上させた。.

目次

• 空気圧理論の基本原理とは何か？
• 空気圧縮はどのように空気圧エネルギーを生み出すのか？
• 空気圧システムを支配する熱力学原理とは何か？
• 空気圧部品はどのように空気エネルギーを機械的仕事に変換するのか？
• 空気圧システムにおけるエネルギー伝達メカニズムとは何か？
• 空気圧理論は産業システム設計にどのように適用されるのか？
• 結論
• 空気圧理論に関するよくある質問

空気圧理論の基本原理とは何か？

空気圧理論は、エネルギー変換、伝達、および産業用途における利用を含む、圧縮空気システムを支配する科学的原理を包括する。.

空気圧理論は、熱力学的エネルギー変換、気流のための流体力学、力発生のための機械的原理、システム自動化のための制御理論に基づいており、統合された圧縮空気動力システムを構築する。.

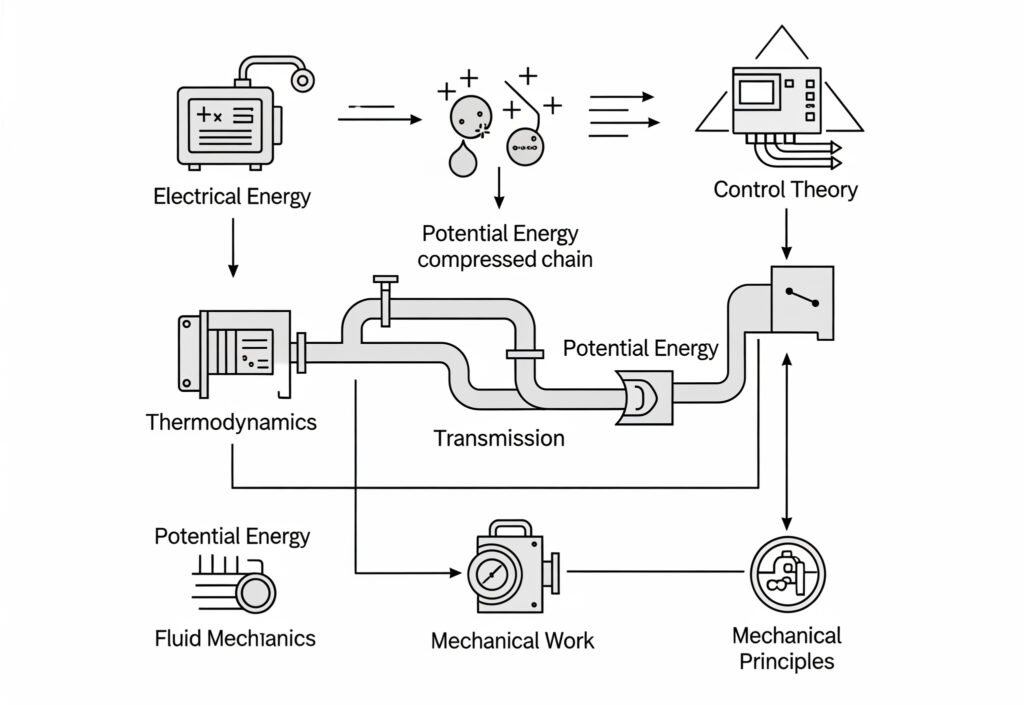
エネルギー変換チェーン

空気圧システムは、電気エネルギーを圧縮空気を通じて機械的仕事に変換する体系的なエネルギー変換プロセスによって作動する。.

エネルギー変換シーケンス：

1. 電気から機械へ電動モーターがコンプレッサーを駆動する
2. 機械式から空気圧式へコンプレッサーは圧縮空気を生成します
3. 空気圧式貯蔵レシーバーに貯蔵された圧縮空気
4. 空気圧伝達配管を通じて供給される空気
5. 空気圧式から機械式へアクチュエータは空気圧力を仕事に変換する

エネルギー効率分析：

コンバージョンステージ	標準効率	エネルギー損失源
電気モーター	90-95%	熱、摩擦、磁気損失
エアコンプレッサー	80-90%	熱、摩擦、漏れ
空気分配	85-95%	圧力低下、漏れ
空気圧アクチュエータ	80-90%	摩擦、内部漏れ
全体システム	55-75%	累積損失

圧縮空気としてのエネルギー媒体

圧縮空気は空気圧システムにおけるエネルギー伝達媒体として機能し、圧力ポテンシャルを通じてエネルギーを蓄積・輸送する。.

空気エネルギー貯蔵の原理：

蓄積エネルギー = P × V × ln(P/P₀)

場所：

• P = 圧縮空気圧力
• V = 貯蔵容量
• P₀ = 大気圧

エネルギー密度の比較：

• 圧縮空気（100 PSI）: 0.5 BTU/立方フィート
• 油圧作動油（1000 PSI）: 0.7 BTU/立方フィート
• 電気電池: 50～200 BTU/立方フィート
• ガソリン: 1ガロンあたり36,000 BTU

システム統合理論

空気圧理論は、部品間の相互作用と全体的な性能を最適化するシステム統合の原則を包含する。.

統合の原則：

• 圧力マッチング互換性のある圧力向けに設計された部品
• フローマッチング空気供給は消費要求に合致する
• 応答マッチングアプリケーション向けに最適化されたシステムタイミング
• 制御統合調整されたシステム運用

基本支配方程式

空気圧理論は、システムの挙動と性能を記述する基本方程式に基づいている。.

基本空気力学方程式：

原則	方程式	申請
理想気体の法則2	PV = nRT	空気挙動予測
戦力生成	F = P × A	アクチュエータ出力力
流量	Q = Cd × A × √(2ΔP/ρ)	気流計算
作業成果	W = P × ΔV	エネルギー変換
パワー	P = F × v	システム電源要件

空気圧縮はどのように空気圧エネルギーを生み出すのか？

空気圧縮は、体積を減らし圧力を高めることで大気中の空気を高エネルギーの圧縮空気に変換し、空気圧システムのエネルギー源を生み出す。.

空気圧縮は熱力学的プロセスを通じて空気圧エネルギーを生成する。このプロセスでは機械的作業が大気中の空気を圧縮し、増加した圧力として位置エネルギーを蓄積する。この蓄積されたエネルギーは解放され、有用な仕事を行うことができる。.

圧縮熱力学

空気圧縮は、エネルギー要求量、温度変化、およびシステム効率を決定する熱力学原理に従う。.

圧縮プロセスの種類：

プロセス種別	特性	エネルギー方程式	アプリケーション
等温3	一定温度	W = P₁V₁ln(P₂/P₁)	冷却を伴う低速圧縮
断熱	熱伝達なし	W = (P₂V₂ - P₁V₁) / (γ - 1)	急速圧縮
ポリトロピック	実世界のプロセス	W = (P₂V₂ - P₁V₁) / (n - 1)	実際のコンプレッサーの作動

場所：

• γ = 比熱比（空気の場合1.4）
• n = 多項式指数（典型的には1.2～1.35）

コンプレッサーの種類と理論

異なるコンプレッサーの種類は、空気圧縮を実現するために様々な機械的原理を利用している。.

容積式圧縮機：

往復式コンプレッサー：

• 理論ピストン運動が体積変化を生む
• 圧縮比P₂/P₁ = (V₁/V₂)ⁿ
• 効率性: 70-85% 体積効率
• アプリケーション高圧、間欠運転

ロータリースクリューコンプレッサー：

• 理論メッシュ状のローターが空気を閉じ込め圧縮する
• 圧縮連続プロセス
• 効率性85-95% 体積効率
• アプリケーション連続運転、中程度の圧力

ダイナミックコンプレッサー：

遠心圧縮機：

• 理論インペラーは運動エネルギーを伝達し、それが圧力に変換される
• 圧力上昇ΔP = ρ(U₂² – U₁²)/2
• 効率性: 75-85% 総合効率
• アプリケーション: 大容量、低～中程度の圧力

圧縮エネルギー要求

空気圧縮の理論的および実際のエネルギー要求は、システムの電力需要と運転コストを決定する。.

理論圧縮力：

等温発電P = (mRT/550) × ln(P₂/P₁)
断熱出力P = (mRT/550) × (γ/(γ-1)) × [(P₂/P₁)^((γ-1)/γ) – 1]

実際の電力要件：

制動馬力 = 理論出力 ÷ 総合効率

消費電力の例：

圧力（PSI）	CFM	理論上のHP	実効HP（75%）
100	100	18.1	24.1
100	500	90.5	120.7
150	100	23.8	31.7
200	100	28.8	38.4

発熱と管理

空気圧縮は多量の熱を発生させるため、システム効率と部品保護のためにこの熱を管理する必要がある。.

発熱理論：

発生熱量 = 入力仕事量 – 有効圧縮仕事量

断熱圧縮の場合：
温度上昇 = T₁[(P₂/P₁)^((γ-1)/γ) – 1]

冷却方法：

• 空冷自然換気または強制換気
• 水冷熱交換器は圧縮熱を除去する
• インタークーリング中間冷却を伴う多段圧縮
• 後冷却空気貯蔵前の最終冷却

空気圧システムを支配する熱力学原理とは何か？

熱力学の原理は、空気圧システムにおけるエネルギー変換、熱伝達、効率を支配し、システムの性能と設計要件を決定する。.

空気熱力学は、熱力学第一法則および第二法則、気体挙動方程式、熱伝達機構、ならびにシステムの効率と性能に影響を与えるエントロピーに関する考察を扱う。.

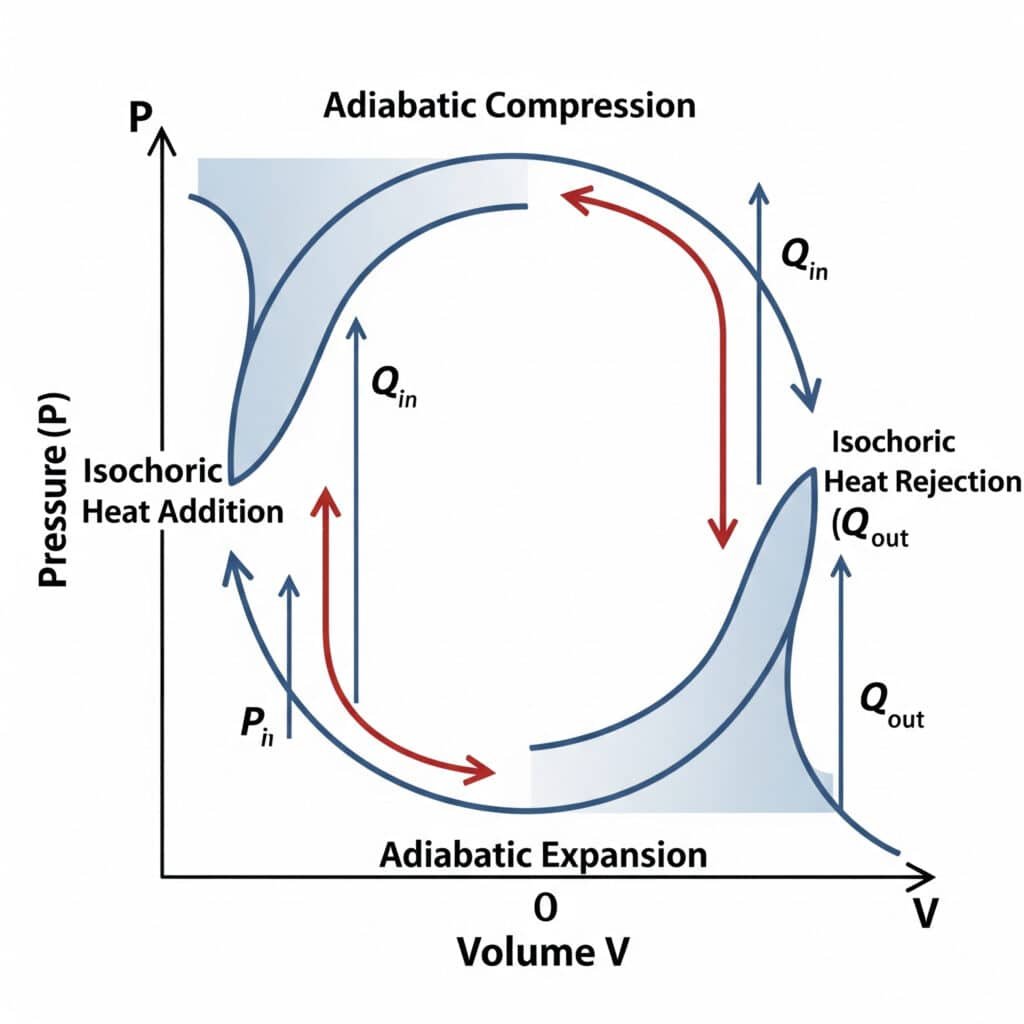
第一法則の応用

第一法則（熱力学第一法則）は、空気圧システムにおけるエネルギー保存則を規定し、仕事入力、熱伝達、および内部エネルギー変化を関連付ける。.

第一法則方程式：

ΔU = Q – W

場所：

• ΔU = 内エネルギーの変化
• Q = システムに加えられる熱量
• W = 系が行う仕事

空気圧応用：

• 圧縮プロセス仕事が入力されると、内部エネルギーと温度が増加する
• 拡張プロセス仕事が行われると内部エネルギーは減少する
• 熱伝達システムの効率と性能に影響を与えます
• エネルギーバランス総エネルギー入力は、有用な仕事と損失の合計に等しい

熱力学第二法則の影響

第二法則は理論上の最大効率を決定し、システム性能を低下させる不可逆過程を特定する。.

エントロピーに関する考察：

ΔS ≥ Q/T （不可逆過程について）

空気圧システムにおける不可逆プロセス：

• 摩擦損失機械的エネルギーを熱に変換する
• スロットリング損失仕事量なしに圧力低下
• 熱伝達温度差はエントロピーを生み出す
• 混合プロセス異なる圧力流の混合

空気圧システムにおけるガスの挙動

実際の気体の挙動は、特定の条件下では理想気体の仮定から外れ、システムの性能計算に影響を与える。.

理想気体の仮定：

• 体積を持たない点分子
• 分子間力なし
• 弾性衝突のみ
• 温度に比例する運動エネルギー

実ガス補正：

ファンデルワールス式(P + a/V²) (V – b) = RT

ここで、a および b は、以下の要素を考慮したガス固有の定数である：

• a: 分子間引力
• b: 分子体積効果

圧縮率⁴:

Z = PV/(nRT)

• Z = 1（理想気体の場合）
• 実ガス挙動の場合、Z ≠ 1

空気圧システムにおける熱伝達

熱伝達は、空気密度、圧力、および部品の動作に影響を与える温度変化を通じて、空気圧システムの性能に影響を及ぼす。.

熱伝達のモード：

モード	メカニズム	空気圧アプリケーション
伝導	直接接触熱伝達	配管壁、部品加熱
対流	流体運動熱伝達	空冷、熱交換器
放射線	電磁熱伝達	高温用途

熱伝達効果：

• 空気密度の変化温度は空気の密度と流れに影響を与える
• コンポーネント拡張熱膨張はクリアランスに影響する
• 結露冷却により結露が生じる可能性があります
• システム効率熱損失は利用可能なエネルギーを減少させる

空気圧システムにおける熱力学サイクル

空気圧システムは、効率と性能特性を決定する熱力学的サイクルを通じて作動する。.

基本空気圧サイクル：

1. 圧縮大気中の空気をシステム圧力まで圧縮したもの
2. ストレージ一定圧力下で貯蔵された圧縮空気
3. 拡張アクチュエータを通じて空気が膨張し、仕事を行う
4. 排気膨張した空気が大気中に放出される

サイクル効率分析：

サイクル効率 = 有効仕事出力 / エネルギー入力

典型的な空気圧サイクル効率：20-40%（原因：）

• 圧縮効率の低さ
• 圧縮時の熱損失
• 配電における電圧降下
• アクチュエータの膨張損失
• 排気エネルギーは回収されない

最近、ノルウェーの製造技術者であるラース・アンデルセン氏の空気圧システムの熱力学最適化を支援しました。適切な熱回収の実施と絞り損失の最小化により、システム全体の効率を28%から41%に改善し、運用コストを35%削減しました。.

空気圧部品はどのように空気エネルギーを機械的仕事に変換するのか？

空圧部品は、圧縮空気のエネルギーを、圧力と流量を力、運動、トルクに変換する様々な機構を通じて、有用な機械的仕事へと変換する。.

空気圧エネルギー変換は、直線運動には圧力と面積の関係、運動には圧力と体積の膨張を利用し、回転運動には特殊機構を用いる。効率は構成部品の設計と作動条件によって決定される。.

リニアアクチュエータのエネルギー変換

線形 空気圧アクチュエータ 空気圧をピストン・シリンダー機構を通じて線形力と運動に変換する。.

戦力生成理論：

F = P × A – 摩擦力 – ばね力

場所：

• P = システム圧力
• A = 有効ピストン面積
• F_friction = 摩擦損失
• F_spring = 戻りばね力（単動式）

作業量算出：

仕事 = 力 × 距離 = P × A × ストローク

出力電力：

パワー = 力 × 速度 = P × A × (ds/dt)

シリンダーの種類と性能

異なるシリンダー設計は、特定の用途と性能要件に合わせてエネルギー変換を最適化します。.

単動シリンダー：

• エネルギー源一方向のみの圧縮空気
• リターン機構スプリング式または重力式リターン
• 効率性: 60-75%（ばね損失による）
• アプリケーション: 簡易な位置決め、低負荷用途

複動シリンダー：

• エネルギー源両方向の圧縮空気
• 出力両方向への完全な圧力
• 効率性: 75-85%（適切な設計による）
• アプリケーション高力・高精度アプリケーション

性能比較：

シリンダータイプ	強制（延長）	力（引き込み）	効率性	費用
単動式	P × A – ばねの引力	F_springのみ	60-75%	低
複動式	P × A	P × (A – A_rod)	75-85%	中
ロッドレス	P × A	P × A	80-90%	高

ロータリーアクチュエータのエネルギー変換

ロータリー空気圧アクチュエータは、様々な機械的機構を通じて空気圧を回転運動とトルクに変換する。.

ベーン式ロータリーアクチュエータ：

トルク = P × A × R × η

場所：

• P = システム圧力
• A = 有効ベーン面積
• R = モーメントアーム半径
• η = 機械効率

ラック・アンド・ピニオンアクチュエータ：

トルク = (P × A_ピストン) × R_ピニオン

ここで、R_pinion はピニオン半径であり、直線力を回転トルクに変換する。.

エネルギー変換効率係数

圧縮空気から有用な仕事への空気圧エネルギー変換効率には、複数の要因が影響する。.

効率低下の要因：

損失源	典型的な損失	緩和策
シール摩擦	5-15%	低摩擦シール、適切な潤滑
内部リーク	2-10%	品質保証マーク、適切なクリアランス
圧力降下	5-20%	適切なサイズ選定、短い接続
発熱	10-20%	冷却効率に優れた設計
機械的摩擦	5-15%	高品質ベアリング、アライメント

全体変換効率：

η_total = η_シール × η_漏れ × η_圧力 × η_機械的

標準的な範囲：適切に設計されたシステムでは60-80%

動的性能特性

空気圧アクチュエータの性能は、負荷条件、速度要件、およびシステムダイナミクスによって異なる。.

力-速度関係：

一定圧力および流量において：

• 高負荷低速、高力
• 低負荷高速、低力
• 定常電力力 × 速度 = 定数

応答時間要因：

• 空気の圧縮性: 時間の遅れを生じさせる
• ボリューム効果: 大容量ほど応答が遅くなる
• 流量制限応答速度の制限
• 制御弁応答システムダイナミクスに影響を与える

空気圧システムにおけるエネルギー伝達メカニズムとは何か？

空気圧システムにおけるエネルギー伝達は、損失を最小限に抑えながら圧縮空気エネルギーを供給源から使用点まで輸送する複数のメカニズムを伴う。.

空気圧エネルギー伝達は、流体力学および熱力学の原理に基づき、配管ネットワークを通じた圧力伝達、バルブおよび継手による流量制御、ならびにレシーバーにおけるエネルギー貯蔵を利用する。.

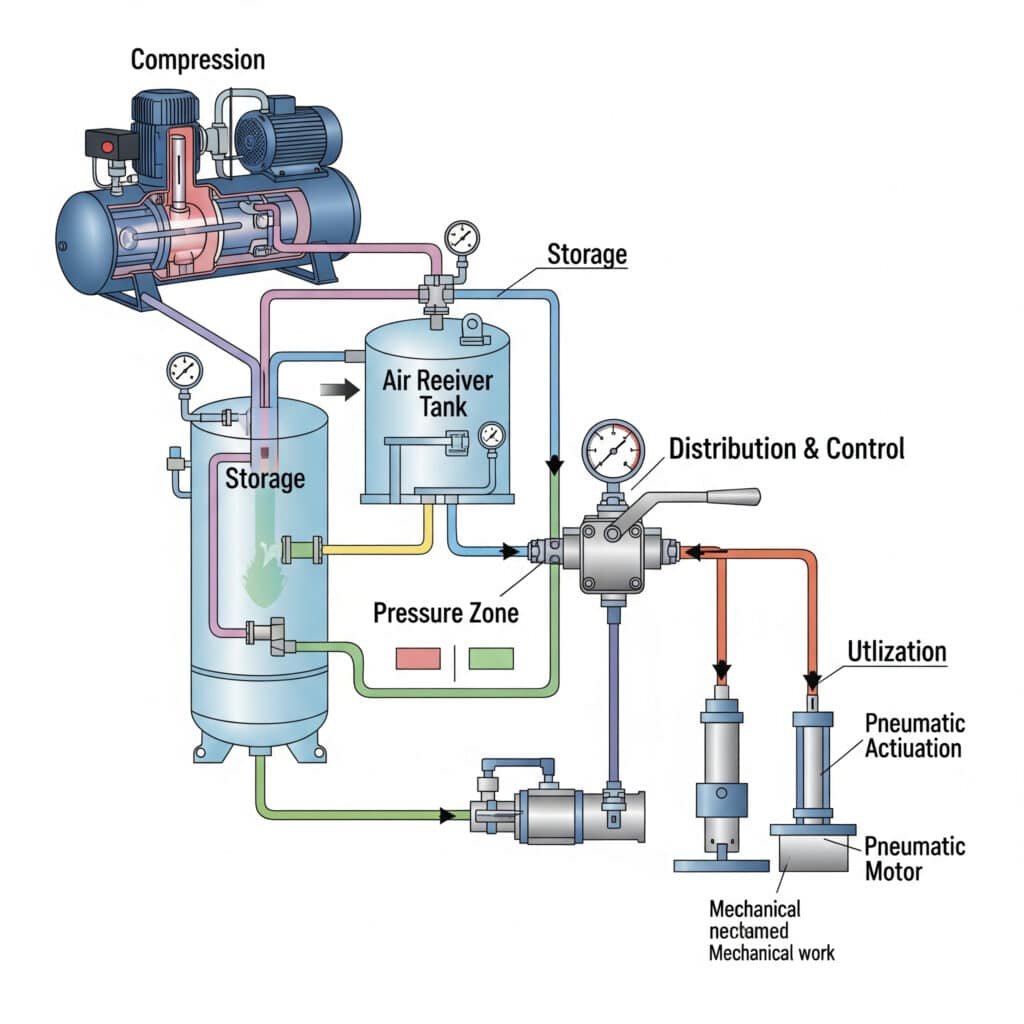
圧力伝達理論

圧縮空気エネルギーは、空気媒体中を音速で伝播する圧力波を介して空気圧システムを通じて伝達される。.

圧力波の伝播：

波の速度 = √(γRT) = √(γP/ρ)

場所：

• γ = 比熱比（空気の場合1.4）
• R = 気体定数
• T = 絶対温度
• P = 圧力
• ρ = 空気密度

圧力伝達特性：

• 波の速度標準状態の空気中では約1,100フィート毎秒
• 圧力平衡接続システム全体で高速に
• 距離効果: 一般的な空気圧システムにおける最小限の構成
• 周波数特性高周波圧力変化が減衰した

流れに基づくエネルギー伝達

空気圧システムによるエネルギー伝達は、アクチュエータや構成部品に圧縮空気を供給する空気流量に依存する。.

質量流エネルギー伝達：

エネルギー流量 = ṁ × h

場所：

• ṁ = 質量流量
• h = 圧縮空気の比エンタルピー

体積流量に関する考慮事項：

Q_actual = Q_standard × (P_standard/P_actual) × (T_actual/T_standard)

エネルギーの流動関係：

• 高流量: 迅速なエネルギー供給、即応性
• 低流量エネルギー供給が遅く、反応が遅延する
• 流量制限エネルギー伝達効率を低下させる
• フロー制御エネルギー供給速度を調節する

配電系統のエネルギー損失

空気圧分配システムではエネルギー損失が発生し、システムの効率と性能を低下させる。.

主な損失要因：

損失の種類	原因	典型的な損失	緩和
摩擦損失	管壁摩擦	2-10 PSI	適切な配管サイズ選定
フィッティング損失	流れの乱れ	1-5 PSI	継手を最小限に抑える
漏れ損失	システム漏洩	10-40%	定期メンテナンス
圧力降下	流量制限	5-15 PSI	制限を撤廃する

圧力損失計算：

ΔP = f × (L/D) × (ρV²/2)

場所：

• f = 摩擦係数
• L = 配管長
• D = パイプ径
• ρ = 空気密度
• V = 空気速度

エネルギー貯蔵と回収

空気圧システムは、効率と性能を向上させるためにエネルギー貯蔵と回収機構を利用する。.

圧縮空気貯蔵：

蓄積エネルギー = P × V × ln(P/P₀)

ストレージの利点：

• ピーク需要一時的な高需要への対応
• 圧力安定性圧力を一定に保つ
• エネルギーバッファ需要変動を平準化する
• システム保護圧力変動を防止する

エネルギー回収の機会：

• 排気熱回収: 拡張エネルギーを捕捉する
• 熱回収圧縮熱を利用する
• 圧力回復部分的に膨張した空気の再利用
• 再生システム多段式エネルギー回収

制御システム エネルギー管理

空気圧制御システムは、エネルギー伝達を管理し、性能を最適化しながら消費を最小限に抑える。.

制御戦略：

• 圧力調整最適な圧力レベルを維持する
• フロー制御需要と供給を一致させる
• シーケンス制御複数のアクチュエータを協調させる
• エネルギー監視消費を追跡し最適化する

高度制御技術：

• 可変圧力負荷要件に合わせて圧力を調整する
• 需要ベース制御必要な時のみ給気する
• 負荷検知実際の需要に基づいてシステムを調整する
• 予測制御エネルギー需要を予測する

空気圧理論は産業システム設計にどのように適用されるのか？

空気圧理論は、性能要件を満たしつつエネルギー消費と運用コストを最小化する、効率的で信頼性の高い産業用空気圧システムの設計における科学的基盤を提供する。.

産業用空気圧システムの設計は、熱力学原理、流体力学、制御理論、機械工学を応用し、製造、自動化、プロセス制御用途向けに最適化された圧縮空気システムを構築する。.

システム設計方法論

空気圧システムの設計は、理論的原理を実用的な要求事項に応用する体系的な方法論に従う。.

設計プロセスのステップ：

1. 要件分析性能仕様を定義する
2. 理論計算: 空気圧の原理を適用する
3. 部品選定最適なコンポーネントを選択する
4. システム統合: 構成要素間の相互作用を調整する
5. パフォーマンス最適化エネルギー消費を最小限に抑える
6. 安全性分析安全な運転を確保する

設計基準の考慮事項：

設計係数	理論的根拠	実践的応用
必要戦力	F = P × A	アクチュエータの選定
速度要件	流量計算	バルブと配管のサイズ選定
エネルギー効率	熱力学的解析	コンポーネント最適化
応答時間	動的解析	制御システム設計
信頼性	故障モード解析	部品選定

圧力レベル最適化

最適なシステム圧力は、性能要件とエネルギー効率および部品コストのバランスを保つ。.

圧力選択理論：

最適圧力 = f(力要件, エネルギーコスト, 部品コスト)

圧力レベル分析：

• 低圧（50-80 PSI）: エネルギーコストの削減、大型部品
• 中圧（80-120 PSI）バランスの取れた性能と効率
• 高圧（120-200 PSI）コンパクトな部品、より高いエネルギーコスト

圧力のエネルギー影響：

電力 ∝ P^0.286 （等温圧縮の場合）

20%の圧力増加 = 5.4%の出力増加

コンポーネントのサイズ設定と選定

理論計算により、システム性能と効率に対する最適な構成要素サイズが決定される。.

アクチュエータの選定：

必要圧力 = (荷重力 + 安全係数) / 有効面積

バルブサイズ選定：

Cv = Q × √(ρ/ΔP)

場所：

• Cv = バルブ流量係数
• Q = 流量
• ρ = 空気密度
• ΔP = 圧力損失

配管サイズ最適化：

経済直径 = K × (Q/v)^0.4

ここで、Kはエネルギーコストと配管コストに依存する。.

システム統合理論

空気圧システムの統合は、制御理論とシステムダイナミクスを適用して構成部品の動作を調整する。.

統合の原則：

• 圧力マッチングコンポーネントは互換性のある圧力で動作します
• フローマッチング供給能力は需要に見合う
• 応答マッチングシステムタイミングの最適化
• 制御統合調整されたシステム運用

システムダイナミクス：

伝達関数⁵ 出力/入力 = K/(τs + 1)

場所：

• K = システム利得
• τ = 時間定数
• s = ラプラス変数

エネルギー効率最適化

理論的解析により、空気圧システムにおけるエネルギー効率向上の機会が特定される。.

効率最適化戦略：

戦略	理論的根拠	潜在的な節約額
圧力最適化	熱力学的解析	10-30%
漏洩除去	質量保存則	20-40%
コンポーネントの適正規模化	フロー最適化	5-15%
熱回収	省エネルギー	10-20%
制御最適化	システムダイナミクス	5-25%

ライフサイクルコスト分析：

総費用 = 初期費用 + 運営費用 × 現在価値係数

運転コストには、システムの寿命期間にわたるエネルギー消費量が含まれる。.

最近、マイケル・オブライエンというオーストラリアの製造エンジニアと共同で、空圧システムの再設計プロジェクトの理論的検証を行いました。適切な空圧理論の原則を適用することで、システム設計を最適化し、52%のエネルギー削減を達成すると同時に、性能を35%向上させ、メンテナンスコストを40%削減しました。.

安全理論の応用

空気圧安全理論は、性能と効率を維持しながらシステムが安全に動作することを保証する。.

安全分析手法：

• ハザード分析潜在的な安全上のリスクを特定する
• リスク評価確率と結果を定量化する
• 安全システム設計: 保護措置を実施する
• 故障モード解析コンポーネントの故障を予測する

安全設計の原則：

• フェイルセーフ設計システムがセーブ状態に失敗しました
• 冗長性複数の保護システム
• エネルギー隔離蓄積されたエネルギーを除去する能力
• 圧力解放過圧状態を防止する

結論

空気圧理論は、熱力学的エネルギー変換、流体力学、および圧縮空気システムを支配する制御原理を包含し、効率的で信頼性の高い産業用自動化および製造システムの設計における科学的基盤を提供する。.

空気圧理論に関するよくある質問

1. 物理系におけるエネルギー、熱、仕事、エントロピーを支配する基本原理である、ゼロ法則、第一法則、第二法則、第三法則を含む熱力学の基礎原理の概要を提供する。. ↩

2. 理想気体の法則（PV=nRT）について詳細に説明する。これは、様々な条件下におけるほとんどの気体の挙動を近似し、圧力、体積、温度、および気体の量を関連付ける基本的な状態方程式である。. ↩

3. 等温（一定温度）、断熱（熱移動なし）、および多変温（熱移動を許容）という主要な熱力学的プロセスを説明し比較する。これらは現実世界のガス圧縮と膨張をモデル化する上で極めて重要である。. ↩

4. 圧縮率係数（Z）の概念を説明する。これは実ガスが理想気体の挙動から逸脱する度合いを表す補正係数であり、現実の計算においてより高い精度を得るために理想気体の法則を修正するために用いられる。. ↩

5. 伝達関数の定義を提供する。これは制御理論における数学的表現であり、線形時不変システムの入力と出力の関係をラプラス領域でモデル化するものである。. ↩