
Heb je ooit een pneumatische cilinder na continu in bedrijf te zijn geweest en verbaasd te zijn over hoe warm het aanvoelt? Die hitte is niet alleen een ongemak, maar staat ook voor energieverspilling, verminderde efficiëntie en potentiële betrouwbaarheidsproblemen die uw bedrijf duizenden euro's kunnen kosten.
Warmteoverdracht in pneumatische systemen vindt plaats via drie mechanismen: geleiding door componentmaterialen, convectie tussen oppervlakken en lucht en straling van hete oppervlakken. Inzicht in en optimalisatie van deze principes kan de bedrijfstemperaturen met 15-30% verlagen, de levensduur van componenten tot 40% verlengen en de energie-efficiëntie met 5-15% verbeteren.
Vorige maand gaf ik advies aan een voedselverwerkingsbedrijf in Georgia waar hun cilinders zonder staaf het elke 3-4 maanden begaven vanwege thermische problemen. Hun onderhoudsteam verving simpelweg onderdelen zonder de hoofdoorzaak aan te pakken. Door de juiste principes voor warmteoverdracht toe te passen, verlaagden we de bedrijfstemperaturen met 22°C en verlengden we de levensduur van de componenten tot meer dan een jaar. Ik zal u laten zien hoe we dat hebben gedaan en hoe u dezelfde principes op uw systemen kunt toepassen.
Inhoudsopgave
- Berekening geleidingscoëfficiënt: Hoe beweegt warmte door uw onderdelen?
- Convectiebevorderende methoden: Welke technieken maximaliseren de lucht-oppervlakte warmteoverdracht?
- Stralingsefficiëntiemodel: Wanneer is warmtestraling van belang in pneumatische systemen?
- Conclusie
- Veelgestelde vragen over warmteoverdracht in pneumatische systemen
Berekening geleidingscoëfficiënt: Hoe beweegt warmte door uw onderdelen?
Geleiding is het primaire mechanisme voor warmteoverdracht binnen vaste pneumatische componenten. Begrijpen hoe je geleidingscoëfficiënten moet berekenen en optimaliseren is essentieel voor het beheren van systeemtemperaturen.
De warmtegeleidingscoëfficiënt kan worden berekend met Wet van Fourier1q = -k(dT/dx), waarbij q de warmteflux is (W/m²), k de warmtegeleidingscoëfficiënt (W/m-K) en dT/dx de temperatuurgradiënt. Voor pneumatische onderdelen hangt de effectieve geleiding af van de materiaalkeuze, de kwaliteit van de interface en geometrische factoren die de lengte van het warmtetraject en de doorsnede beïnvloeden.
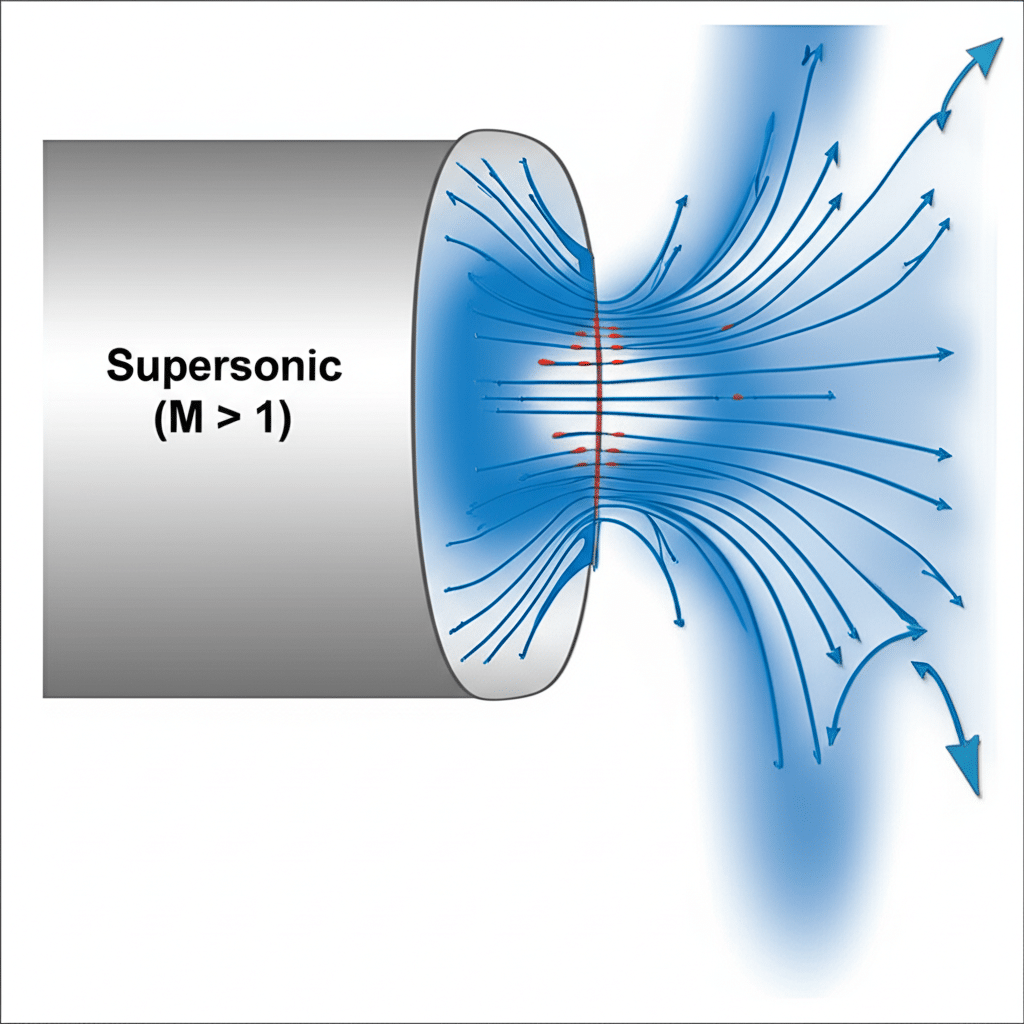
Ik herinner me dat ik een probleem oploste bij een productielijn in Tennessee waar de lagers van de cilinder zonder stang het voortijdig begaven. Het onderhoudsteam had zonder succes meerdere smeermiddelen geprobeerd. Toen we de geleidingswegen analyseerden, ontdekten we een thermisch knelpunt op het raakvlak tussen lager en behuizing. Door de oppervlakteafwerking te verbeteren en een warmtegeleidende compound aan te brengen, verhoogden we de effectieve geleidingscoëfficiënt met 340% en verdwenen de storingen volledig.
Fundamentele geleidingsvergelijkingen
Laten we de belangrijkste vergelijkingen voor het berekenen van geleiding in pneumatische componenten eens op een rijtje zetten:
Wet van Fourier voor warmtegeleiding
De basisvergelijking voor warmtegeleiding is:
q = -k(dT/dx)
Waar:
- q = warmtestroom (W/m²)
- k = warmtegeleidingsvermogen (W/m-K)
- dT/dx = Temperatuurgradiënt (K/m)
Voor een eenvoudig eendimensionaal geval met constante doorsnede:
Q = kA(T₁-T₂)/L
Waar:
- Q = warmteoverdrachtsnelheid (W)
- A = Dwarsdoorsnede (m²)
- T₁, T₂ = temperaturen aan elk uiteinde (K)
- L = lengte van het warmtetraject (m)
Warmteweerstandsconcept
Voor complexe geometrieën is de warmteweerstandbenadering vaak praktischer:
R = L/(kA)
Waar:
- R = warmteweerstand (K/W)
Voor systemen met meerdere componenten in serie:
Rtotaal = R₁ + R₂ + R₃ + ... + Rₙ
En de warmteoverdracht wordt:
Q = ΔT/Rtotaal
Vergelijking van materiaalthermische geleidbaarheid
| Materiaal | Warmtegeleidingsvermogen (W/m-K) | Relatieve geleidbaarheid | Algemene toepassingen |
|---|---|---|---|
| Aluminium | 205-250 | Hoog | Cilinders, koellichamen |
| Staal | 36-54 | Medium | Structurele onderdelen |
| Roestvrij staal | 14-16 | Laag-Middelmatig | Corrosieve omgevingen |
| Brons | 26-50 | Medium | Lagers, bussen |
| PTFE | 0.25 | Zeer laag | Afdichtingen, lagers |
| Nitrilrubber | 0.13 | Zeer laag | O-ringen, afdichtingen |
| Lucht (stilstaand) | 0.026 | Extreem Laag | Gatenvuller |
| Thermische pasta | 3-8 | Laag | Interfacemateriaal |
Contactweerstand in pneumatische assemblages
Bij interfaces tussen componenten heeft de contactweerstand een grote invloed op de warmteoverdracht:
Rcontact = 1/(hc × A)
Waar:
- hc = contactcoëfficiënt (W/m²-K)
- A = contactoppervlak (m²)
Factoren die de contactweerstand beïnvloeden zijn onder andere:
- Oppervlakteruwheid: Ruwe oppervlakken hebben minder contactoppervlak
- Contactdruk: Hogere druk verhoogt het effectieve contactoppervlak
- Interface Materialen: Thermische verbindingen vullen luchtlekken
- Reinheid van het oppervlak: Verontreinigingen kunnen de weerstand verhogen
Casestudie: Stangloze cilinder thermische optimalisatie
Voor een magnetische cilinder zonder staaf die thermische problemen ondervindt:
| Component | Origineel ontwerp | Geoptimaliseerd ontwerp | Verbetering |
|---|---|---|---|
| Cilinderhuis | Geanodiseerd aluminium | Zelfde materiaal, verbeterde afwerking | 15% betere geleiding |
| Lagerinterface | Contact van metaal op metaal | Thermische verbinding toegevoegd | 340% betere geleiding |
| Montagebeugels | Gelakt staal | Blank aluminium | 280% betere geleiding |
| Algemene thermische weerstand | 2,8 K/W | 0,7 K/W | 75% reductie |
| Bedrijfstemperatuur | 78°C | 56°C | 22°C reductie |
| Levensduur van onderdelen | 4 maanden | >12 maanden | 3× verbetering |
Praktische geleidingsoptimalisatietechnieken
Op basis van mijn ervaring met honderden pneumatische systemen zijn dit de meest effectieve benaderingen om de geleiding te verbeteren:
Optimalisatie van de interface
- Oppervlakteafwerking: Verbeter de gladheid van het paringsoppervlak tot Ra 0,4-0,8 μm
- Thermische interfacematerialen2: Breng geschikte verbindingen aan (3-8 W/m-K)
- Aandraaimoment bevestigingsmiddel: Zorg voor een juiste aandraaing voor een optimale contactdruk
- Netheid: Verwijder alle olie en verontreinigingen vóór de montage
Strategieën voor materiaalselectie
- Kritische warmtetrajecten: Gebruik materialen met een hoge geleidbaarheid (aluminium, koper)
- Thermische onderbrekingen: Gebruik bewust materialen met een laag geleidingsvermogen om warmte te isoleren
- Samengestelde benaderingen: Combineer materialen voor optimale prestaties/kosten
- Anisotrope materialen: Gebruik waar nodig gerichte geleiding
Geometrische optimalisatie
- Warmteweglengte: Minimaliseer de afstand tussen warmtebronnen en koellichamen
- Dwarsdoorsnede: Maximaliseer oppervlakte loodrecht op warmtestroom
- Thermische knelpunten: Beperkingen in het warmtetraject identificeren en elimineren
- Overbodige paden: Meerdere parallelle geleidingsroutes creëren
Convectiebevorderende methoden: Welke technieken maximaliseren de lucht-oppervlakte warmteoverdracht?
Convectie is vaak de beperkende factor bij het koelen van pneumatische systemen. Het verbeteren van de convectieve warmteoverdracht kan het thermisch beheer en de systeemprestaties aanzienlijk verbeteren.
Convectieve warmteoverdracht volgt De afkoelingswet van Newton3: Q = hA(Ts-T∞), waarbij h de convectiecoëfficiënt is (W/m²-K), A het oppervlak en (Ts-T∞) het temperatuurverschil tussen het oppervlak en de vloeistof. Verbeteringsmethoden omvatten het vergroten van het oppervlak door vinnen, het verbeteren van de vloeistofsnelheid door een gerichte luchtstroom en het optimaliseren van de oppervlaktekenmerken om turbulente grenslagen te bevorderen.
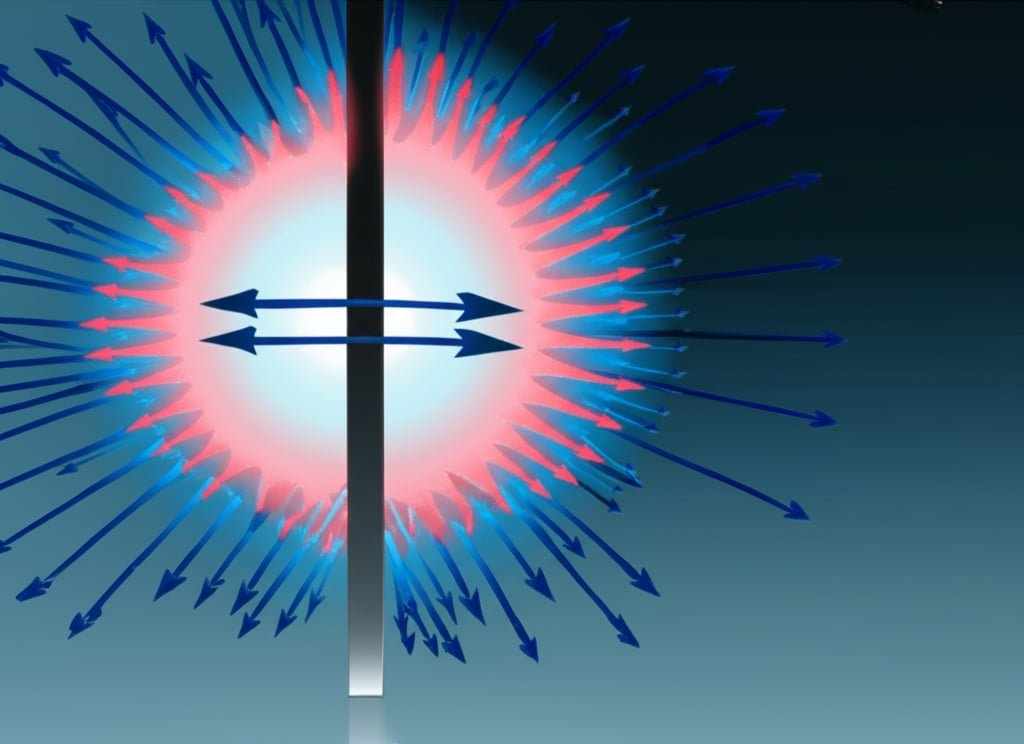
Tijdens een energie-efficiëntie-audit bij een verpakkingsbedrijf in Arizona kwam ik een pneumatisch systeem tegen dat in een omgeving van 43°C werkte. De cilinders zonder staaf raakten oververhit ondanks dat ze aan alle onderhoudsvereisten voldeden. Door het implementeren van een gerichte convectieverbetering - het toevoegen van kleine aluminium vinnen en een ventilator met laag vermogen - verhoogden we de convectiecoëfficiënt met 450%. Hierdoor daalde de bedrijfstemperatuur van gevaarlijke niveaus tot binnen de specificaties zonder grote systeemaanpassingen.
Grondbeginselen van convectiewarmteoverdracht
De basisvergelijking voor convectieve warmteoverdracht is:
Q = hA(Ts-T∞)
Waar:
- Q = warmteoverdrachtsnelheid (W)
- h = convectiecoëfficiënt (W/m²-K)
- A = oppervlakte (m²)
- Ts = oppervlaktetemperatuur (K)
- T∞ = temperatuur vloeistof (lucht) (K)
De convectiecoëfficiënt h hangt af van meerdere factoren:
- Vloeistofeigenschappen (dichtheid, viscositeit, thermische geleidbaarheid)
- Stromingseigenschappen (snelheid, turbulentie)
- Oppervlaktegeometrie en -oriëntatie
- Stromingsregime (natuurlijke vs. geforceerde convectie)
Natuurlijke convectie vs. geforceerde convectie
| Parameter | Natuurlijke convectie | Geforceerde convectie | Implicaties |
|---|---|---|---|
| Typische h-waarde | 5-25 W/m²-K | 25-250 W/m²-K | Geforceerde convectie kan 10× effectiever zijn |
| Drijvende kracht | Drijfvermogen (temperatuurverschil) | Externe druk (ventilatoren, blowers) | Gedwongen convectie is minder afhankelijk van temperatuur |
| Stroompatroon | Verticale stroming langs oppervlakken | Richtinggevoelig op basis van het forceringmechanisme | Geforceerde stroming kan worden geoptimaliseerd voor specifieke componenten |
| Betrouwbaarheid | Passief, altijd aanwezig | Stroom en onderhoud nodig | Natuurlijke convectie zorgt voor basiskoeling |
| Benodigde ruimte | Vrije ruimte nodig voor luchtcirculatie | Ruimte nodig voor luchtverplaatsers en leidingen | Gedwongen systemen hebben meer planning nodig |
Technieken voor convectieverbetering
Oppervlaktevergroting
Het effectieve oppervlak vergroten door:
Vinnen en verlengde oppervlakken
- Pin vinnen: Omnidirectionele luchtstroom, 150-300% oppervlaktevergroting
- Plaatvinnen: Gerichte luchtstroom, 200-500% oppervlaktevergroting
- Gegolfde oppervlakken: Matige verbetering, 50-150% oppervlaktetoenameOpruwen van het oppervlak
- Microtexturering: 5-15% effectieve oppervlaktevergroting
- Gedimde oppervlakken: 10-30% toename plus grenslaageffecten
- Patronen met groeven: 15-40% verhoging met richtingsvoordelen
Flow Manipulatie
Verbetering van de luchtstroomkenmerken door:
Geforceerde luchtsystemen
- Ventilatoren: gerichte luchtstroom, 200-600% h verbetering
- Blazers: Hogedrukstroom, 300-800% h verbetering
- Persluchtstralen: Gerichte koeling, 400-1000% lokale h verbeteringStroompadoptimalisatie
- Baffles: Sturen lucht naar kritieke onderdelen
- Venturi-effecten: Versnellen lucht over specifieke oppervlakken
- Vortexgeneratoren: Turbulentie creëren voor grenslaagverstoring
Oppervlakte aanpassingen
Oppervlakte-eigenschappen veranderen om convectie te verbeteren:
Emissiviteitsbehandelingen
- Zwarte oxide: Verhoogt de emissiviteit tot 0,7-0,9
- Anodiseren: Gecontroleerde emissiviteit van 0,4-0,9
- Verven en coatings: Aanpasbare emissiviteit tot 0,98Beheersing van bevochtigbaarheid
- Hydrofiele coatings: Verbeteren vloeistofkoeling
- Hydrofobische oppervlakken: Voorkomt condensatieproblemen
- Gepatenteerde bevochtigbaarheid: Gerichte condensaatstroom
Praktisch implementatievoorbeeld
Voor een staafloze pneumatische cilinder die werkt in een omgeving met hoge temperaturen:
| Verbeteringsmethode | Implementatie | h Verbetering | Temperatuurverlaging |
|---|---|---|---|
| Pin Vinnen (6mm) | Aluminium clip-on vinnen, 10 mm tussenruimte | 180% | 12°C |
| Gerichte luchtstroom | 80 mm, 2 W DC-ventilator op 1,5 m/s | 320% | 18°C |
| Oppervlaktebehandeling | Zwart anodiseren | 40% | 3°C |
| Gecombineerde aanpak | Alle methoden geïntegreerd | 450% | 24°C |
Nusseltgetalcorrelatie voor ontwerpberekeningen
Voor technische berekeningen moet de Nusselt-getal4 (Nu) geeft een dimensieloze benadering van convectie:
Nu = hL/k
Waar:
- L = karakteristieke lengte
- k = warmtegeleidingscoëfficiënt van vloeistof
Voor geforceerde convectie over een vlakke plaat:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminaire stroming)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulente stroming)
Waar:
- Re = Reynoldsgetal (snelheid × lengte × dichtheid / viscositeit)
- Pr = Prandtl-getal (soortelijke warmte × viscositeit / warmtegeleidingsvermogen)
Met deze correlaties kunnen ingenieurs convectiecoëfficiënten voorspellen voor verschillende configuraties en de koelstrategieën dienovereenkomstig optimaliseren.
Stralingsefficiëntiemodel: Wanneer is warmtestraling van belang in pneumatische systemen?
Straling wordt vaak over het hoofd gezien bij het thermisch beheer van pneumatische systemen, maar het kan verantwoordelijk zijn voor 15-30% van de totale warmteoverdracht in veel toepassingen. Begrijpen wanneer en hoe de stralingswarmteoverdracht geoptimaliseerd kan worden is cruciaal voor een compleet thermisch beheer.
Stralingswarmteoverdracht volgt de Wet van Stefan-Boltzmann5: Q = εσA(T₁⁴-T₂⁴), waarbij ε de oppervlakte-emissiviteit is, σ de Stefan-Boltzmann constante, A de oppervlakte en T₁ en T₂ de absolute temperaturen van het uitstralende oppervlak en de omgeving. De stralingsefficiëntie in pneumatische systemen hangt voornamelijk af van de emissiviteit van het oppervlak, het temperatuurverschil en de aanzichtfactoren tussen de componenten en hun omgeving.
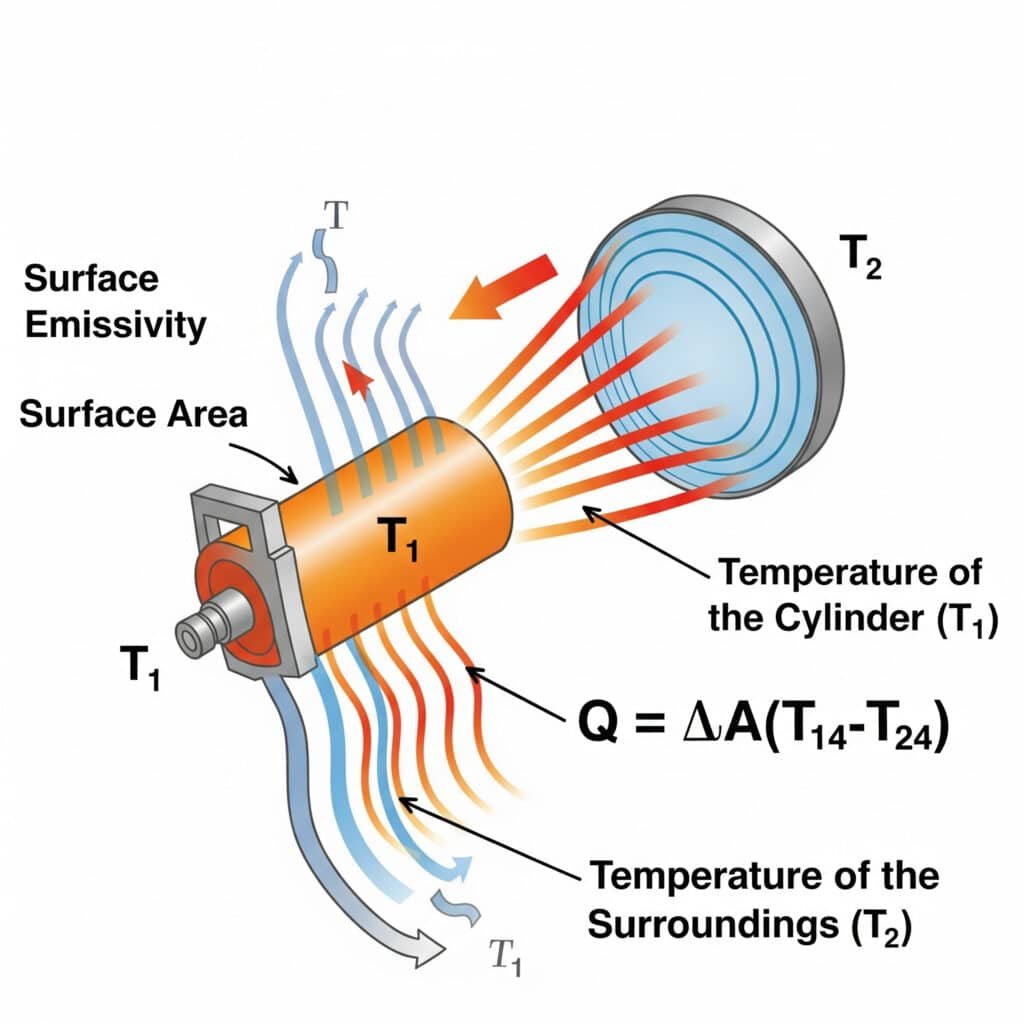
Onlangs heb ik een fabrikant van halfgeleiderapparatuur in Oregon geholpen bij het oplossen van oververhittingsproblemen met hun precisiecilinders zonder staaf. Hun ingenieurs hadden zich uitsluitend gericht op geleiding en convectie, maar hadden straling over het hoofd gezien. Door een coating met hoge emissiviteit aan te brengen (verhoging van ε van 0,11 naar 0,92), verbeterden we de stralingswarmteoverdracht met meer dan 700%. Deze eenvoudige, passieve oplossing verlaagde de bedrijfstemperaturen met 9°C zonder bewegende delen of energieverbruik - een kritische vereiste in hun cleanroomomgeving.
Grondbeginselen van stralingswarmteoverdracht
De basisvergelijking voor stralingswarmteoverdracht is:
Q = εσA(T₁⁴-T₂⁴)
Waar:
- Q = warmteoverdrachtsnelheid (W)
- ε = emissiviteit (dimensieloos, 0-1)
- σ = constante van Stefan-Boltzmann (5,67 × 10-⁸ W/m²-K⁴)
- A = oppervlakte (m²)
- T₁ = absolute oppervlaktetemperatuur (K)
- T₂ = absolute temperatuur omgeving (K)
Emissiviteitswaarden van het oppervlak voor gebruikelijke pneumatische materialen
| Materiaal/Oppervlak | Emissiviteit (ε) | Stralingsefficiëntie | Verbeterpotentieel |
|---|---|---|---|
| Gepolijst aluminium | 0.04-0.06 | Zeer slecht | >1500% verbetering mogelijk |
| Geanodiseerd aluminium | 0.7-0.9 | Uitstekend | Al geoptimaliseerd |
| Roestvrij staal (gepolijst) | 0.07-0.14 | Slecht | >600% verbetering mogelijk |
| Roestvrij staal (geoxideerd) | 0.6-0.85 | Goed | Matige verbetering mogelijk |
| Staal (gepolijst) | 0.07-0.10 | Slecht | >900% verbetering mogelijk |
| Staal (geoxideerd) | 0.7-0.9 | Uitstekend | Al geoptimaliseerd |
| Geschilderde oppervlakken | 0.8-0.98 | Uitstekend | Al geoptimaliseerd |
| PTFE (wit) | 0.8-0.9 | Uitstekend | Al geoptimaliseerd |
| Nitrilrubber | 0.86-0.94 | Uitstekend | Al geoptimaliseerd |
Bekijk Factor Overwegingen
Stralingsuitwisseling is niet alleen afhankelijk van emissiviteit, maar ook van geometrische relaties tussen oppervlakken:
F₁₂ = Fractie van straling die oppervlak 1 verlaat en oppervlak 2 treft
Voor complexe geometrieën kunnen aanzichtfactoren worden berekend met:
- Analytische oplossingen voor eenvoudige geometrieën
- Bekijk factor algebra voor het combineren van bekende oplossingen
- Numerieke methoden voor complexe regelingen
- Empirische benaderingen voor praktische techniek
Temperatuursafhankelijkheid van straling
De vierde macht temperatuurrelatie maakt straling vooral effectief bij hogere temperaturen:
| Oppervlaktetemperatuur | Percentage warmteoverdracht door straling* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Uitgaande van natuurlijke convectie, ε = 0,8, 25°C omgeving.
Strategieën voor verbetering van stralingsefficiëntie
Op basis van mijn ervaring met industriële pneumatische systemen zijn dit de meest effectieve benaderingen om de stralingswarmteoverdracht te verbeteren:
Emissiviteitswijziging van het oppervlak
Coatings met hoog doorlaatvermogen
- Zwart anodiseren voor aluminium (ε ≈ 0,8-0,9)
- Zwarte oxide voor staal (ε ≈ 0,7-0,8)
- Speciale keramische coatings (ε ≈ 0,9-0,98)Oppervlaktestructurering
- Micro-ruw maken verhoogt de effectieve emissiviteit
- Poreuze oppervlakken verbeteren de stralingseigenschappen
- Gecombineerde emissiviteit/convectieverhoging
Milieu-optimalisatie
Temperatuurbeheer omgeving
- Afscherming van hete apparatuur/processen
- Koel muren/plafonds voor betere stralingsuitwisseling
- Reflecterende barrières om straling naar koelere oppervlakken te leidenBekijk Factor Verbetering
- Oriëntatie voor maximale blootstelling aan koele oppervlakken
- Verwijderen van blokkerende objecten
- Reflectoren om de stralingsuitwisseling met koelere gebieden te verbeteren
Casestudie: Stralingsverbetering in precisie-pneumatiek
Voor een zeer nauwkeurige cilinder zonder stang in een cleanroomomgeving:
| Parameter | Origineel ontwerp | Stralingsondersteund ontwerp | Verbetering |
|---|---|---|---|
| Materiaal oppervlak | Gepolijst aluminium (ε ≈ 0,06) | Keramisch gecoat aluminium (ε ≈ 0,94) | 1467% toename in emissiviteit |
| Warmteoverdracht door straling | 2.1W | 32.7W | 1457% toename in straling |
| Bedrijfstemperatuur | 68°C | 59°C | 9°C reductie |
| Levensduur van onderdelen | 8 maanden | >24 maanden | 3× verbetering |
| Implementatiekosten | – | $175 per cilinder | 4,2 maanden terugverdientijd |
Straling vs. andere manieren van warmteoverdracht
Begrijpen wanneer straling domineert is cruciaal voor efficiënt thermisch beheer:
| Voorwaarde | Geleidingsdominantie | Convectie dominantie | Stralingsdominantie |
|---|---|---|---|
| Temperatuurbereik | Laag naar hoog | Laag tot gemiddeld | Gemiddeld tot hoog |
| Materiaaleigenschappen | Hoge k-materialen | Lage k, hoog oppervlak | Hoge ε oppervlakken |
| Omgevingsfactoren | Goed thermisch contact | Bewegende lucht, ventilatoren | Groot temperatuurverschil |
| Ruimtebeperkingen | Strakke verpakking | Open luchtstroom | Uitzicht op koelere omgeving |
| Beste toepassingen | Component interfaces | Algemene koeling | Hete oppervlakken, vacuüm, stilstaande lucht |
Conclusie
Het beheersen van de principes van warmteoverdracht - berekening van de geleidingscoëfficiënt, methoden voor convectieverhoging en modellering van de stralingsefficiënt - vormt de basis voor effectief thermisch beheer in pneumatische systemen. Door deze principes toe te passen, kunt u de bedrijfstemperaturen verlagen, de levensduur van componenten verlengen en de energie-efficiëntie verbeteren, terwijl u een betrouwbare werking kunt garanderen, zelfs in veeleisende omgevingen.
Veelgestelde vragen over warmteoverdracht in pneumatische systemen
Wat is de typische temperatuurstijging in pneumatische cilinders tijdens het gebruik?
Pneumatische cilinders hebben meestal te maken met temperatuurstijgingen van 20-40°C boven de omgevingstemperatuur tijdens continue werking. Deze stijging is het gevolg van wrijving tussen afdichtingen en cilinderwanden, compressieverhitting van lucht en mechanische arbeid die wordt omgezet in warmte. Stangloze cilinders hebben vaak te maken met hogere temperatuurstijgingen (30-50°C) vanwege hun complexere afdichtingssystemen en geconcentreerde warmteontwikkeling in de lager/afdichting.
Hoe beïnvloedt de werkdruk de warmteontwikkeling in pneumatische systemen?
De werkdruk heeft een aanzienlijke invloed op de warmteontwikkeling, waarbij hogere drukken via verschillende mechanismen meer warmte creëren. Elke verhoging van de werkdruk met 1 bar verhoogt de warmteontwikkeling met 8-12% als gevolg van grotere wrijvingskrachten tussen afdichtingen en oppervlakken, hogere compressieverhitting en verhoogde lekgerelateerde verliezen. Deze relatie is ongeveer lineair binnen het normale werkbereik (3-10 bar).
Wat is de optimale koelmethode voor pneumatische componenten in verschillende omgevingen?
De optimale koelmethode verschilt per omgeving: in schone omgevingen met gematigde temperaturen (15-30°C) is natuurlijke convectie met de juiste afstand tussen de componenten vaak voldoende. In omgevingen met hoge temperaturen (30-50°C) is geforceerde convectie met ventilatoren of perslucht nodig. In extreem hete omstandigheden (>50°C) of waar de luchtstroom beperkt is, kunnen actieve koelmethoden zoals thermo-elektrische koelers of vloeistofkoeling nodig zijn. In alle gevallen zorgt het maximaliseren van de straling door oppervlakken met een hoge emissiviteit voor extra passieve koeling.
Hoe bereken ik de totale warmteoverdracht van een pneumatisch component?
Bereken de totale warmteoverdracht door de bijdragen van elk mechanisme bij elkaar op te tellen: Qtotaal = Qgeleiding + Qvectie + Qstraling. Gebruik voor geleiding Q = kA(T₁-T₂)/L voor elk warmtetraject. Gebruik voor convectie Q = hA(Ts-T∞) met de juiste convectiecoëfficiënten. Gebruik voor straling Q = εσA(T₁⁴-T₂⁴). In de meeste industriële pneumatische toepassingen die werken bij 30-80°C is de verdeling bij benadering 20-40% geleiding, 40-70% convectie en 10-30% straling.
Wat is de relatie tussen temperatuur en de levensduur van pneumatische onderdelen?
De levensduur van componenten neemt exponentieel af met toenemende temperatuur, volgens een gewijzigde Arrhenius-relatie. Als vuistregel geldt dat elke 10°C stijging van de bedrijfstemperatuur de levensduur van afdichtingen en componenten met 40-50% vermindert. Dit betekent dat een onderdeel dat werkt bij 70°C mogelijk slechts een derde zo lang meegaat als hetzelfde onderdeel bij 50°C. Deze relatie is bijzonder kritisch voor polymeercomponenten zoals afdichtingen, lagers en pakkingen, die vaak het onderhoudsinterval voor pneumatische systemen bepalen.
-
Biedt een fundamentele uitleg van de Wet van Fourier, het fundamentele principe dat beschrijft hoe warmte door vaste materialen wordt geleid op basis van hun warmtegeleiding en temperatuurgradiënt. ↩
-
Legt de functie en de soorten Thermal Interface Materials (TIM's) uit, die worden gebruikt om microscopische luchtlekken tussen componenten op te vullen om de warmtegeleiding te verbeteren en de thermische weerstand te verlagen. ↩
-
Gaat in op de principes van de afkoelingswet van Newton, die bepaalt hoe objecten afkoelen door warmte af te geven aan de omringende vloeistof via convectie, een sleutelfactor in het ontwerp van systeemkoeling. ↩
-
Biedt een diepgaande blik op het Nusseltgetal, een kritische dimensieloze grootheid in vloeistofdynamica en warmteoverdracht die de verhouding weergeeft tussen convectieve en geleidende warmteoverdracht over een grens. ↩
-
Beschrijft de Wet van Stefan-Boltzmann, het fundamentele natuurkundige principe dat de totale energie kwantificeert die door een zwart lichaam wordt uitgestraald, wat essentieel is voor het berekenen van warmteverlies van hete oppervlakken. ↩


