De fysica achter vane-type roterende actuators omvat complexe interacties tussen vloeistofdynamica, mechanische krachten en thermodynamica die de meeste ingenieurs nooit volledig begrijpen. Toch is het beheersen van deze principes cruciaal voor het optimaliseren van prestaties, het voorspellen van gedrag en het oplossen van toepassingsproblemen die een project kunnen maken of breken. 🔬
Roterende vaanactuators werken volgens het drukvermenigvuldigingsprincipe van Pascal, waarbij lineaire pneumatische kracht wordt omgezet in een roterend koppel via schuivende vaanmechanismen, waarbij de prestaties worden bepaald door drukverschillen, vaangeometrie, wrijvingscoëfficiënten en thermodynamische gaswetten die de koppeloutput, snelheid en efficiëntiekenmerken bepalen.
Ik heb onlangs gewerkt met een ontwerpingenieur genaamd Jennifer van een ruimtevaartfabriek in Seattle die worstelde met inconsistenties in het koppel van haar toepassing met roterende actuators. Haar actuators produceerden 30% minder koppel dan berekend en veroorzaakten positioneringsfouten bij kritieke assemblagewerkzaamheden. De hoofdoorzaak was niet mechanisch, maar een fundamenteel verkeerd begrip van de fysica die het gedrag van vaanactuators bepaalt. ✈️
Inhoudsopgave
- Hoe genereert de drukdynamica het rotatiekoppel in vaanvormige actuatoren?
- Welke rol speelt de geometrie van de vinnen bij het bepalen van de prestatiekenmerken van de actuator?
- Welke thermodynamische principes beïnvloeden de snelheid en efficiëntie van roterende aandrijvingen?
- Hoe beïnvloeden wrijvingskrachten en mechanische verliezen de prestaties van actuatoren in de praktijk?
Hoe genereert de drukdynamica het rotatiekoppel in vaanvormige actuatoren?
Inzicht in de omzetting van druk naar koppel is van fundamenteel belang voor het ontwerp en de toepassing van roterende actuators.
Actuators van het vaan-type genereren een koppel door drukverschillen die inwerken op de vaanoppervlakken, waarbij het koppel gelijk is aan het drukverschil maal het effectieve vaanoppervlak maal momentarm1 afstand, met de relatie T = ΔP × A × r, aangepast door de vaanhoek en kamergeometrie om roterende beweging te creëren uit lineaire pneumatische krachten.
Fundamentele principes voor het genereren van koppel
Pascal's Principe Toepassing
De basis van de werking van een roterende actuator ligt in Pascal's principe2:
- Drukoverdracht: Gelijkmatige druk op alle oppervlakken in de kamer
- Forceer vermenigvuldiging: Druk × oppervlakte = kracht op elk vaanoppervlak
- Een moment creëren: Kracht × straal = koppel om de centrale as
Uitgangspunten voor koppelberekening
Basisformule voor koppel: T = ΔP × A_eff × r_eff × η
Waar:
- T = uitgaand koppel (lb-in)
- ΔP = drukverschil (PSI)
- A_eff = effectief schoepenoppervlak (sq in)
- r_eff = effectieve momentarm (inch)
- η = mechanisch rendement (0,85-0,95)
Drukverdelingsanalyse
Druk in de kamer
De drukverdeling binnen vaankamers is niet uniform:
- Hogedrukkamer: Toevoerdruk min stromingsverliezen
- Lagedrukkamer: Uitlaatdruk plus tegendruk
- Overgangszones: Drukgradiënten bij vaanranden
- Dode volumes: Opgesloten lucht in vrije ruimten
Effectieve oppervlakteberekeningen
| Windvaanconfiguratie | Formule voor effectief oppervlak | Efficiëntiefactor |
|---|---|---|
| Enkele schoep | A = L × W × sin(θ) | 0.85-0.90 |
| Dubbele vaan | A = 2 × L × B × sin(θ/2) | 0.88-0.93 |
| Multi-Vaan | A = n × L × W × sin(θ/n) | 0.90-0.95 |
Waarbij L = vaanlengte, W = vaanbreedte, θ = rotatiehoek, n = aantal vinnen.
Dynamische drukeffecten
Door stroming veroorzaakte drukverliezen
Drukdynamica in de echte wereld omvat ook stromingsverliezen:
- Inlaatbeperkingen: Drukverliezen van kleppen en fittingen
- Interne stromingsverliezen: Turbulentie en wrijving in kamers
- Uitlaatbeperkingen: Tegendruk van uitlaatsystemen
- Versnellingsverliezen: Druk die nodig is om bewegende lucht te versnellen
De ruimtevaarttoepassing van Jennifer had te lijden onder een ontoereikende dimensionering van de toevoerleiding, waardoor een drukdaling van 15 PSI optrad tijdens snelle actuatorbewegingen. Dit drukverlies, in combinatie met dynamische stromingseffecten, verklaarde de koppelvermindering van 30% die ze ondervond. 📉
Welke rol speelt de geometrie van de vinnen bij het bepalen van de prestatiekenmerken van de actuator?
De geometrie van de schoepen heeft een directe invloed op het geleverde koppel, de rotatiehoek, de snelheid en het rendement.
De vaangeometrie bepaalt de prestaties van de actuator door de lengte van de vaan (beïnvloedt de torsiearm), de breedte (bepaalt het drukgebied), de dikte (beïnvloedt de afdichting en wrijving), de hoekverhoudingen (bepaalt het rotatiebereik) en de speling (beïnvloedt lekkage en efficiëntie), waarbij elke parameter moet worden geoptimaliseerd voor specifieke toepassingen.
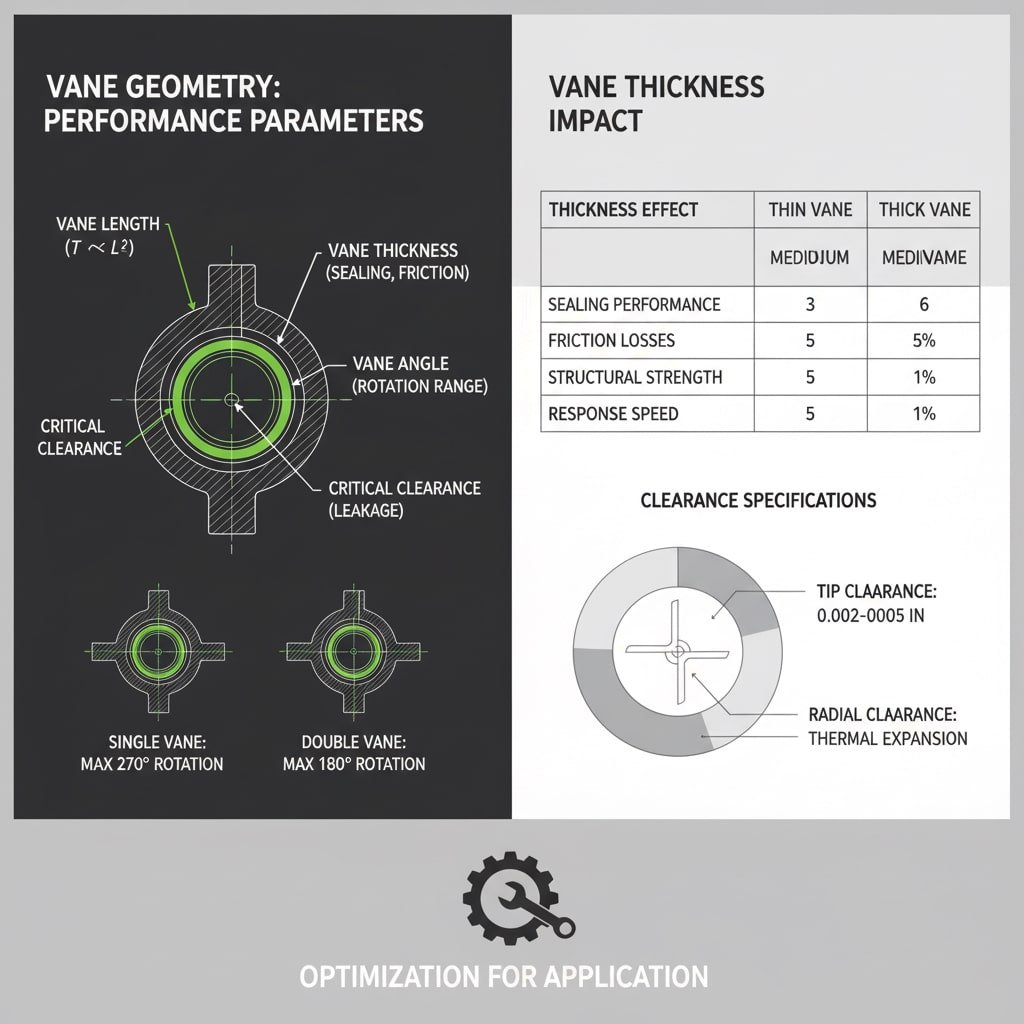
Geometrische parameteranalyse
Optimalisatie vaanlengte
De vaanlengte heeft een directe invloed op het koppelvermogen en de structurele integriteit:
- Koppelverhouding: T ∝ L² (verhouding lengte kwadraat)
- Stressoverwegingen: De buigspanning neemt toe met de lengte in kubieke meters
- Afbuigeffecten: Langere vinnen hebben meer tipdoorbuiging
- Optimale verhoudingen: Lengte-breedteverhoudingen van 3:1 tot 5:1 leveren de beste prestaties
Schoep dikte Impact
De dikte van de vinnen beïnvloedt meerdere prestatieparameters:
| Dikte-effect | Dunne lamellen (< 0,25″) | Middelgrote lamellen (0,25″-0,5″) | Dikke lamellen (> 0,5″) |
|---|---|---|---|
| Afdichtingsprestaties | Slecht - hoge lekkage | Goed - voldoende contact | Uitstekend - stevige afdichtingen |
| Wrijvingsverliezen | Laag | Medium | Hoog |
| Structurele sterkte | Slecht - problemen met doorbuiging | Goed - voldoende stijfheid | Uitstekend - stijf |
| Reactiesnelheid | Snel | Medium | Langzaam |
Overwegingen voor hoekgeometrie
Beperkingen van de rotatiehoek
De vaangeometrie beperkt de maximale draaihoeken:
- Enkele vaan: Maximaal ~270° rotatie
- Dubbele vaan: Maximaal ~180° rotatie
- Meerdere schoepen: Rotatie beperkt door vaaninterferentie
- Kamerontwerp: Geometrie behuizing beïnvloedt bruikbare hoek
Optimalisatie van de schoephoek
De hoek tussen de schoepen beïnvloedt de koppeleigenschappen:
- Gelijke afstand: Levert soepel koppel
- Ongelijke afstand: Kan koppelcurves optimaliseren voor specifieke toepassingen
- Progressieve hoeken: Compenseren voor drukvariaties
Vrije ruimte en afdichtingsgeometrie
Kritieke ontruimingsspecificaties
De juiste speling zorgt voor een evenwicht tussen afdichtingseffectiviteit en wrijving:
- Tip opruiming: 0,002″-0,005″ voor optimale afdichting
- Zijspeling: 0,001″-0,003″ om binding te voorkomen
- Radiale speling: Overwegingen bij temperatuurexpansie
- Axiale speling: Druklager en thermische groei
Bij Bepto maakt ons proces voor optimalisatie van de geometrie van de schoepen gebruik van computationele vloeistofdynamica (CFD)3 analyse gecombineerd met empirische tests om de ideale balans te vinden tussen koppel, snelheid en efficiëntie voor elke toepassing. Dankzij deze engineeringaanpak hebben we een 15-20% hogere efficiëntie bereikt dan standaardontwerpen. 🔧
Welke thermodynamische principes beïnvloeden de snelheid en efficiëntie van roterende aandrijvingen?
Thermodynamische effecten hebben een grote invloed op de prestaties van actuators, vooral bij toepassingen met hoge snelheden of hoge belasting.
Thermodynamische principes die van invloed zijn op roterende actuatoren zijn onder andere gasexpansie en -compressie tijdens rotatie, warmteontwikkeling door wrijving en drukverliezen, temperatuureffecten op luchtdichtheid en viscositeit, en adiabatische versus isothermische processen die de werkelijke versus theoretische prestaties onder werkelijke bedrijfsomstandigheden bepalen.

Toepassingen gaswet
Effecten van de ideale gaswet
De prestaties van een roterende actuator volgen de gaswetrelaties:
- Druk-volume werk: W = ∫P dV tijdens uitzetting
- Temperatuureffecten: PV = nRT bepaalt de druk-temperatuurrelaties
- Dichtheidsvariaties: ρ = PM/RT beïnvloedt massastroomberekeningen
- Samendrukbaarheid: Echte gaseffecten bij hoge druk
Adiabatische vs. isotherme processen
Bij de werking van een actuator zijn beide procestypen betrokken:
| Procestype | Kenmerken | Prestatie-impact |
|---|---|---|
| Adiabatisch | Geen warmteoverdracht, snelle expansie | Hogere drukdalingen, temperatuurveranderingen |
| Isotherm | Constante temperatuur, langzame expansie | Efficiëntere energieomzetting |
| Polytropisch | Combinatie in de echte wereld | Werkelijke prestaties tussen uitersten |
Warmteopwekking en -overdracht
Door wrijving veroorzaakte verwarming
Verschillende bronnen genereren warmte in roterende actuators:
- Wrijving van de vaanpunt: Schuifcontact met behuizing
- Lagerwrijving: Lagerverliezen assteun
- Wrijving van de afdichting: Sleepkrachten roterende afdichting
- Vloeibare wrijving: Viskeuze verliezen in luchtstroming
Berekeningen voor temperatuurstijging
Warmteontwikkeling: Q = μ × N × F × V
Waar:
- Q = warmteproductie (BTU/uur)
- μ = wrijvingscoëfficiënt
- N = rotatiesnelheid (RPM)
- F = normaalkracht (lbs)
- V = schuifsnelheid (ft/min)
Efficiëntie analyse
Thermodynamische efficiëntiefactoren
De algemene efficiëntie combineert meerdere verliesmechanismen:
- Volumetrisch rendement: ηv = werkelijke stroom / theoretische stroom
- Mechanisch rendement: ηm = Uitgangsvermogen / Ingangsvermogen
- Algehele efficiëntie: ηo = ηv × ηm
Strategieën voor efficiëntieoptimalisatie
| Strategie | Efficiëntiewinst | Implementatiekosten |
|---|---|---|
| Verbeterde afdichting | 5-15% | Medium |
| Geoptimaliseerde vrije ruimte | 3-8% | Laag |
| Geavanceerde materialen | 8-12% | Hoog |
| Thermisch beheer | 5-10% | Medium |
Stromingsdynamica en drukverliezen
Effecten van het Reynoldsgetal
De stromingseigenschappen veranderen naargelang de bedrijfsomstandigheden:
- Laminaire stroming: Re < 2300, voorspelbare drukverliezen
- Turbulente stroming: Re > 4000, hogere wrijvingsfactoren
- Overgangsgebied: Onvoorspelbare stroomkarakteristieken
Uit de thermodynamische analyse bleek dat de ruimtevaarttoepassing van Jennifer een aanzienlijke temperatuurstijging doormaakte tijdens snelle cycli, waardoor de luchtdichtheid met 12% afnam en dit bijdroeg aan het koppelverlies. We implementeerden strategieën voor thermisch beheer die de volledige prestaties herstelden. 🌡️
Hoe beïnvloeden wrijvingskrachten en mechanische verliezen de prestaties van actuatoren in de praktijk?
Wrijving en mechanische verliezen verminderen de theoretische prestaties aanzienlijk en moeten zorgvuldig worden beheerd voor een optimale werking van de actuator.
Mechanische verliezen in vaan-type actuatoren omvatten schuifwrijving aan de vaanuiteinden, weerstand van de roterende afdichting, lagerwrijving en interne luchtturbulentie, waardoor het theoretische koppel met 10-20% afneemt en een zorgvuldige materiaalselectie, oppervlaktebehandeling en smeringsstrategieën nodig zijn om de prestatievermindering te minimaliseren.
Wrijvingsanalyse en modellering
Wrijvingsmechanismen voor vaanpunten
De primaire wrijvingsbron doet zich voor op de raakvlakken tussen bus en behuizing:
- Grenssmering: Direct contact van metaal op metaal
- Gemengde smering: Gedeeltelijke scheiding van vloeistoffilm
- Hydrodynamische smering: Volledige vloeistoffilm (zeldzaam in pneumatiek)
Wrijvingscoëfficiëntvariaties
| Materiaalcombinatie | Droge wrijving (μ) | Gesmeerde wrijving (μ) | Temperatuurgevoeligheid |
|---|---|---|---|
| Staal op staal | 0.6-0.8 | 0.1-0.15 | Hoog |
| Staal op brons | 0.3-0.5 | 0.08-0.12 | Medium |
| Staal op PTFE | 0.1-0.2 | 0.05-0.08 | Laag |
| Keramische coating | 0.2-0.3 | 0.06-0.10 | Zeer laag |
Analyse van lagerverlies
Radiale lagerwrijving
De lagers van de uitgaande as dragen aanzienlijk bij aan de verliezen:
- Rolwrijving: Fr = μr × N × r
- Glijdende wrijving: Fs = μs × N
- Viskeuze wrijving: Fv = η × A × V/h
- Wrijving van de afdichting: Extra weerstand door asafdichtingen
Impact van lagerselectie
Verschillende lagertypes beïnvloeden de algemene efficiëntie:
- Kogellagers: Lage wrijving, hoge precisie
- Rollagers: Hogere belastbaarheid, matige wrijving
- Glijlagers: Hoge wrijving, eenvoudige constructie
- Magnetische lagers: Nagenoeg geen wrijving, hoge kosten
Oplossingen voor oppervlaktetechniek
Geavanceerde oppervlaktebehandelingen
Moderne oppervlaktebehandelingen verminderen de wrijving aanzienlijk:
- Hardverchroomd: Vermindert slijtage, matige wrijvingsvermindering
- Keramische coatings: Uitstekende slijtvastheid, lage wrijving
- Diamantachtige koolstof (DLC): Ultralage wrijving, duur
- Gespecialiseerde polymeren: Toepassingsspecifieke oplossingen
Smeerstrategieën
| Smeermethode | Wrijvingsvermindering | Onderhoudsvereisten | Kosten |
|---|---|---|---|
| Olienevelsystemen | 60-80% | Hoog - regelmatige aanvulling | Hoog |
| Vaste smeermiddelen | 40-60% | Laag - lange levensduur | Medium |
| Zelfsmerende materialen | 50-70% | Zeer laag - permanent | Hoge initiële |
| Smeermiddelen met droge film | 30-50% | Middelmatig - periodiek opnieuw aanbrengen | Laag |
Strategieën voor prestatieoptimalisatie
Geïntegreerde ontwerpbenadering
Bij Bepto optimaliseren we wrijving door systematisch ontwerp:
- Materiaalkeuze: Compatibele materiaalparen
- Afwerking oppervlak: Geoptimaliseerde ruwheid voor elke toepassing
- Opruimingscontrole: Minimaliseer de contactdruk
- Thermisch beheer: Temperatuurgeïnduceerde uitzetting controleren
Validatie van prestaties in de praktijk
Laboratoriumtesten versus prestaties in het veld verschillen vaak:
- Inloopeffecten: Prestaties verbeteren bij eerste gebruik
- Gevolgen van besmetting: Realistische vuil- en puineffecten
- Temperatuurcycli: Thermische uitzetting en inkrimping
- Belastingsvariaties: Dynamische belasting versus statische testomstandigheden
Ons uitgebreide wrijvingsanalyse- en optimalisatieprogramma hielp Jennifer's ruimtevaarttoepassing om 95% theoretisch koppel te bereiken - een aanzienlijke verbetering ten opzichte van de oorspronkelijke 70%. De sleutel was het implementeren van een veelzijdige aanpak die geavanceerde materialen, geoptimaliseerde geometrie en de juiste smering combineerde. 🎯
Voorspellende wrijvingsmodellering
Wiskundige wrijvingsmodellen
Nauwkeurige voorspelling van wrijving vereist geavanceerde modellering:
- Coulombwrijving: F = μ × N (basismodel)
- Stribeck-curve: Wrijvingsvariatie met snelheid
- Temperatuureffecten: μ(T) relaties
- Voortgang in slijtage: Wrijving verandert in de loop van de tijd
Conclusie
Inzicht in de fundamentele fysica van vane-type roterende actuatoren - van drukdynamica en thermodynamica tot wrijvingsmechanismen - stelt ingenieurs in staat om prestaties te optimaliseren, gedrag te voorspellen en complexe toepassingsproblemen op te lossen.
Veelgestelde vragen over Vane-type Rotary Actuator Fysica
V: Hoe beïnvloedt de werkdruk de relatie tussen het theoretische en het werkelijke koppel?
Antwoord: Hogere werkdrukken verbeteren over het algemeen de verhouding tussen het theoretische en het werkelijke koppel omdat mechanische verliezen een kleiner percentage van het totale vermogen worden. Een hogere druk verhoogt echter ook de wrijvingskrachten, dus de relatie is niet lineair. De optimale druk is afhankelijk van specifieke toepassingsvereisten en het actuatorontwerp.
V: Waarom verliezen roterende actuators koppel bij hoge snelheden en hoe kan dit worden geminimaliseerd?
A: Koppelverlies bij hoge snelheden ontstaat door verhoogde wrijving, stromingsbeperkingen en thermodynamische effecten. Minimaliseer de verliezen door geoptimaliseerde poortafmetingen, geavanceerde lagersystemen, verbeterde afdichtingsontwerpen en thermisch beheer. Boven bepaalde snelheden vormen stroomsnelheidsbeperkingen de belangrijkste beperking.
V: Welke invloed hebben temperatuurschommelingen op de prestatieberekeningen van rotatieactuators?
A: Temperatuur beïnvloedt de luchtdichtheid (beïnvloedt de kracht), de viscositeit (beïnvloedt de stroming), de materiaaleigenschappen (verandert de wrijving) en de thermische uitzetting (verandert de speling). Een temperatuurstijging van 100 °F kan de koppeloutput met 15-25% verminderen door gecombineerde effecten. Temperatuurcompensatie in regelsystemen helpt om consistente prestaties te behouden.
V: Wat is de relatie tussen de snelheid van de vaanpunt en wrijvingsverliezen in roterende actuators?
A: Wrijvingsverliezen nemen in het algemeen toe met het kwadraat van de tipsnelheid door grotere contactkrachten en warmteontwikkeling. Bij zeer lage snelheden domineert statische wrijving echter, waardoor een complexe relatie ontstaat. Optimale werksnelheden liggen meestal in het middengebied waar dynamische wrijving beheersbaar is.
V: Hoe houd je rekening met luchtcompressie-effecten bij berekeningen van de prestaties van roterende actuators?
A: De samendrukbaarheid van lucht wordt belangrijk bij drukken boven 100 PSI en tijdens snelle acceleratie. Gebruik samendrukbare stromingsvergelijkingen in plaats van onsamendrukbare aannames, houd rekening met drukgolfvoortplantingsvertragingen en houd rekening met adiabatische uitzettingseffecten. Echte gaseigenschappen kunnen nodig zijn voor hogedruktoepassingen boven 200 PSI.
-
Leer de definitie van een momentarm, de loodrechte afstand van een rotatieas tot de actielijn van een kracht, die cruciaal is voor het berekenen van het koppel. ↩
-
Het principe van Pascal begrijpen, de fundamentele wet van de vloeistofmechanica die verklaart hoe druk wordt overgedragen in een afgesloten vloeistof. ↩
-
Verken het gebied van Computational Fluid Dynamics (CFD), een tak van de vloeistofmechanica die numerieke analyse gebruikt om problemen met vloeistofstromingen op te lossen en te analyseren. ↩




