
Está a debater-se com velocidades inconsistentes dos cilindros pneumáticos ou com impactos inesperados no fim do curso? Estes problemas comuns resultam frequentemente de uma má compreensão da cinemática do pistão. Muitos engenheiros concentram-se apenas nos requisitos de força, ignorando os parâmetros críticos de movimento que determinam o desempenho do sistema.
Cinemática do pistão1 têm um impacto direto no desempenho do sistema pneumático através de relações de pressão-velocidade, limites de aceleração e requisitos de amortecimento. A compreensão destes princípios permite aos engenheiros dimensionar corretamente os componentes, prever os perfis de movimento reais e evitar falhas prematuras em cilindros sem haste e outros actuadores pneumáticos.
Nos meus mais de 15 anos na Bepto a trabalhar com sistemas pneumáticos, vi inúmeros casos em que a compreensão destes princípios fundamentais ajudou os clientes a resolver problemas de desempenho persistentes e a prolongar a vida útil do equipamento em 3-5 vezes.
Índice
- Que pressão é realmente necessária para um movimento a velocidade constante?
- Como se calcula a aceleração máxima possível em cilindros pneumáticos?
- Porque é que o tempo de amortecimento é importante e como é calculado?
- Conclusão
- Perguntas frequentes sobre a cinemática do pistão em sistemas pneumáticos
Que pressão é realmente necessária para um movimento a velocidade constante?
Muitos engenheiros aplicam simplesmente a pressão máxima disponível aos seus sistemas pneumáticos, mas esta abordagem é ineficiente e pode levar a movimentos bruscos, desgaste excessivo e desperdício de energia.
A pressão necessária para um movimento de velocidade constante num cilindro pneumático é calculada utilizando P = (F + Fr)/A, em que P é a pressão, F é a força de carga externa, Fr é a resistência de fricção e A é a área do pistão. Este cálculo assegura um funcionamento suave e eficiente sem pressão excessiva que desperdiça energia e acelera o desgaste dos componentes.
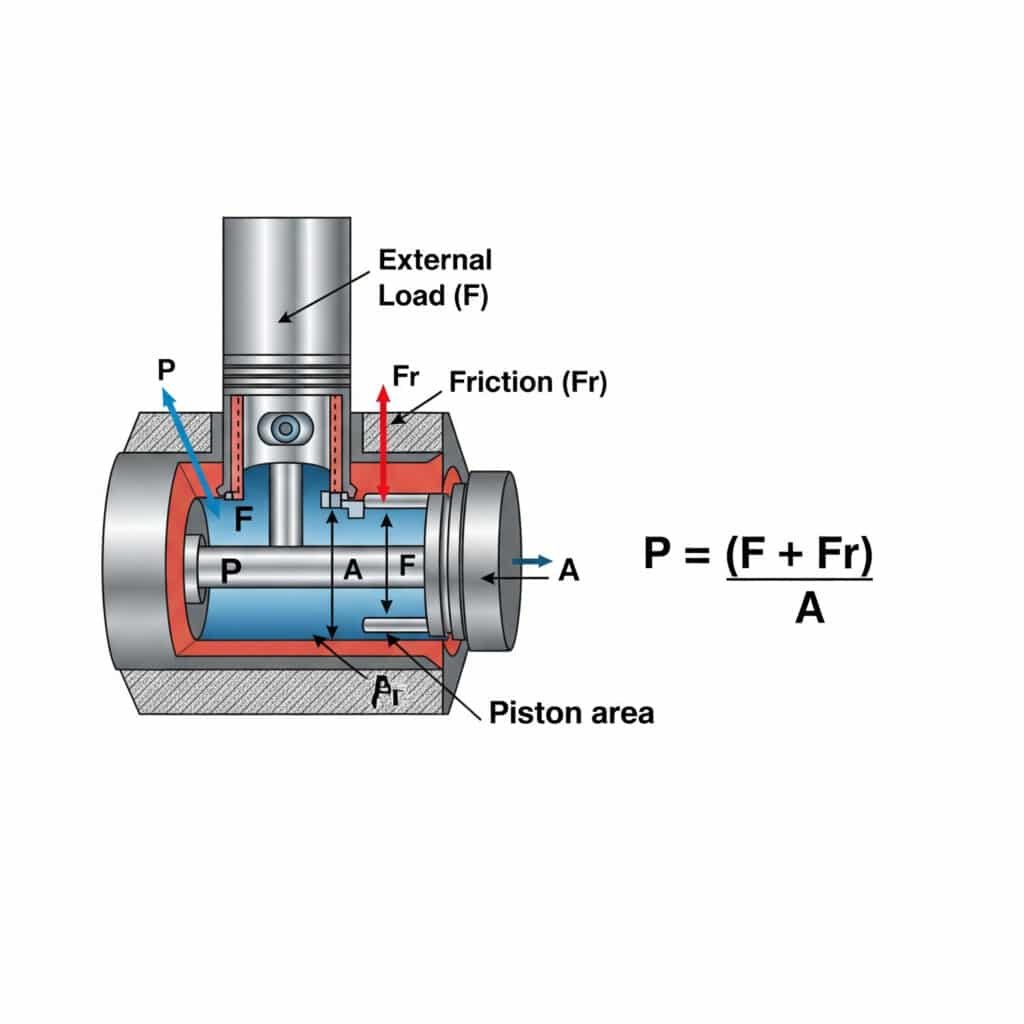
Compreender os requisitos de pressão para o movimento a velocidade constante tem implicações práticas na conceção e funcionamento do sistema. Vou dividir isto em ideias práticas.
Factores que afectam os requisitos de pressão para velocidade constante
A pressão necessária para manter a velocidade constante depende de vários factores:
| Fator | Impacto no requisito de pressão | Considerações práticas |
|---|---|---|
| Carga externa | Relação linear direta | Varia consoante a orientação e as forças externas |
| Atrito | Aumenta a pressão necessária | Alterações com o desgaste e a lubrificação dos vedantes |
| Área do pistão | Inversamente proporcional | Furo maior = menor necessidade de pressão |
| Restrições ao fornecimento de ar | Quedas de pressão nas linhas/válvulas | Dimensionar os componentes para uma queda de pressão mínima |
| Pressão de retorno | Opõe-se à proposta | Considerar a capacidade do caudal de escape |
Cálculo da pressão mínima para um movimento estável
Determinar a pressão mínima necessária para um movimento estável:
- Calcular a força necessária para vencer a carga externa
- Adicionar a força de atrito (normalmente 3-20% da força máxima)
- Dividir pela área efectiva do pistão
- Adicionar um fator de estabilidade (normalmente 10-30%)
Por exemplo, num cilindro sem haste de 40 mm de diâmetro com uma carga de 10 kg e um atrito de 15%:
| Parâmetro | Cálculo | Resultado |
|---|---|---|
| Força de carga | 10kg × 9,81m/s² | 98.1N |
| Força de fricção | 15% de força máxima a 6 bar | ~45N |
| Força total | 98,1N + 45N | 143.1N |
| Área do pistão | π × (0,02m)² | 0.00126m² |
| Pressão mínima | 143,1N ÷ 0,00126m² | 113,571 Pa (1,14 bar) |
| Com 20% Fator de estabilidade | 1,14 bar × 1,2 | 1,37 bar |
Aplicação no mundo real: Poupança de energia através da otimização da pressão
No ano passado, trabalhei com Robert, um engenheiro de produção numa fábrica de mobiliário no Michigan. A sua linha de montagem automatizada utilizava cilindros sem haste que funcionavam a uma pressão de alimentação total de 6 bar, independentemente da carga.
Depois de analisar a sua aplicação, determinámos que a maioria dos movimentos apenas necessitava de 2,5-3 bar para um funcionamento estável. Ao instalar reguladores de pressão proporcionaisreduzimos o consumo de ar em 40%, mantendo o mesmo tempo de ciclo. Isto permitiu poupar aproximadamente $12.000 anualmente em custos de energia, reduzindo o desgaste dos vedantes e aumentando os intervalos de manutenção.
Relação velocidade-pressão em sistemas reais
Na prática, a relação entre pressão e velocidade não é perfeitamente linear devido a:
- Restrições de fluxo: O dimensionamento da válvula e do orifício afecta a velocidade máxima alcançável
- Efeitos de compressibilidade: O ar é compressível, causando atrasos na aceleração
- Fenómenos de stick-slip: As caraterísticas de fricção alteram-se com a velocidade
- Efeitos de inércia: A aceleração da massa requer uma força/pressão adicional
Como se calcula a aceleração máxima possível em cilindros pneumáticos?
A compreensão dos limites de aceleração é crucial para evitar choques excessivos, vibrações e falhas prematuras de componentes em sistemas pneumáticos.
A aceleração máxima possível num cilindro pneumático é calculada utilizando a = (P × A - F - Fr)/m, em que a é a aceleração, P é a pressão, A é a área do pistão, F é a carga externa, Fr é a resistência ao atrito e m é a massa em movimento. Esta equação define os limites físicos da rapidez com que um atuador pneumático pode iniciar ou parar o movimento.
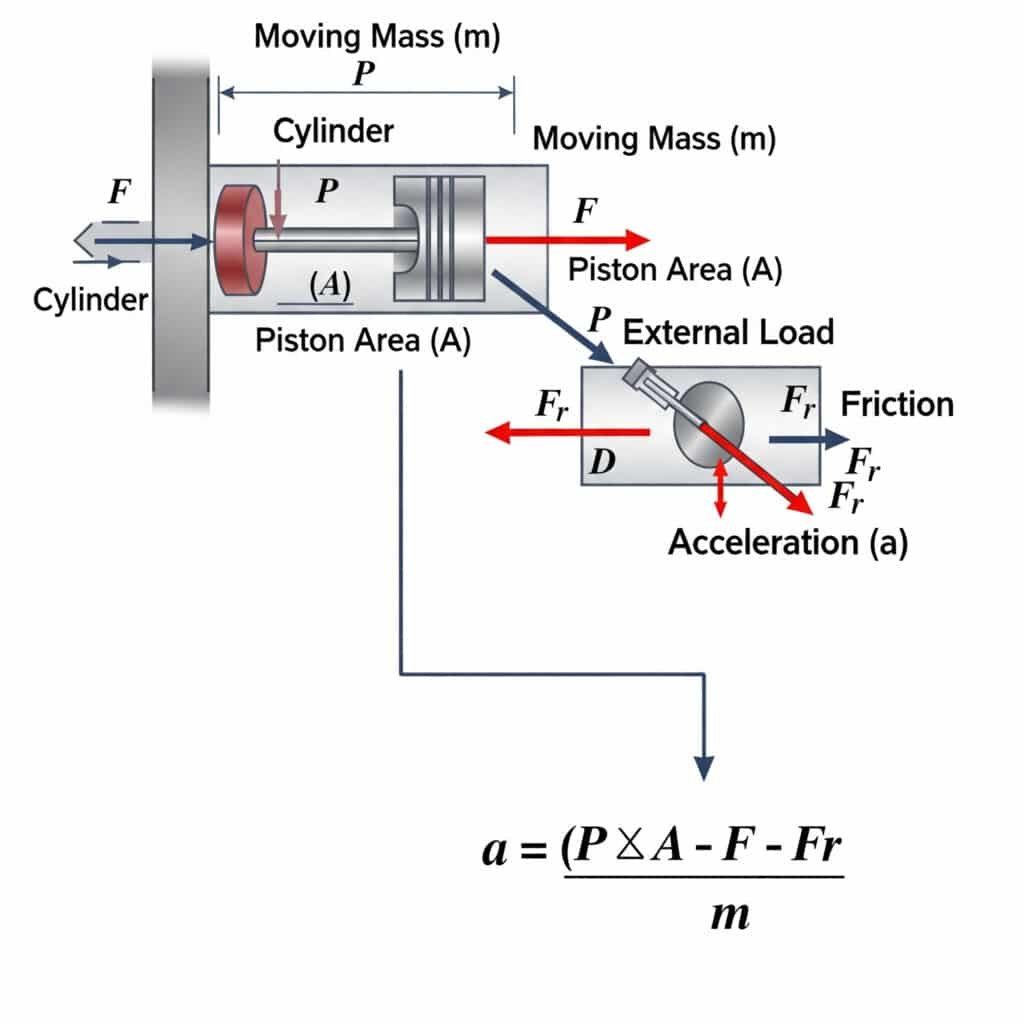
Os limites teóricos de aceleração têm implicações práticas significativas na conceção do sistema e na seleção de componentes.
Derivação da equação do limite de aceleração
A equação do limite de aceleração vem de A segunda lei de Newton2 (F = ma):
- A força líquida disponível para a aceleração é: Fnet = Fpressão - Fcarga - Ffricção
- Fpressão = P × A
- Por conseguinte: a = Fnet/m = (P × A - F - Fr)/m
Limites práticos de aceleração para diferentes tipos de cilindros
As diferentes concepções de cilindros têm diferentes limites práticos de aceleração:
| Tipo de cilindro | Aceleração máxima típica | Factores limitativos |
|---|---|---|
| Cilindro de haste standard | 10-15 m/s² | Encurvadura da haste, cargas de suporte |
| Cilindro sem haste (magnético) | 8-12 m/s² | Força de acoplamento magnético |
| Cilindro sem haste (mecânico) | 15-25 m/s² | Conceção da vedação/rolamento, fricção interna |
| Cilindro guia | 20-30 m/s² | Rigidez do sistema de guias, capacidade de suporte |
| Cilindro de impacto | 50-100+ m/s² | Especialmente concebido para uma aceleração elevada |
Considerações sobre a massa nos cálculos de aceleração
Ao calcular a aceleração, é fundamental incluir todas as massas em movimento:
- Conjunto do pistão: Inclui pistão, vedantes e elementos de ligação
- Massa da carga: Carga externa que está a ser movimentada
- Massa efectiva do ar em movimento: Frequentemente negligenciável, mas relevante em aplicações de alta velocidade
- Massa acrescida devido aos componentes de montagem: Suportes, sensores, etc.
Uma vez ajudei um cliente em França que estava a ter falhas misteriosas no seu sistema de cilindros sem haste. O cilindro estava corretamente dimensionado para a carga de 15 kg indicada, mas falhava sistematicamente após alguns milhares de ciclos.
Após uma investigação, descobrimos que ele não tinha tido em conta a massa de 12 kg da placa de montagem e dos acessórios. A massa real em movimento era quase o dobro da que ele tinha calculado, causando forças de aceleração que excediam os limites de conceção do cilindro. Após a atualização para um cilindro maior, as falhas pararam completamente.
Métodos de controlo da aceleração
Para controlar a aceleração dentro de limites seguros:
- Válvulas de controlo do fluxo: Limitar o caudal durante o movimento inicial
- Válvulas proporcionais: Proporcionar uma subida de pressão controlada
- Aceleração em várias fases: Utilizar aumentos de pressão escalonados
- Amortecimento mecânico: Adicionar amortecedores externos
- Controlo eletrónico: Utilizar sistemas servo-pneumáticos3 com retroação da aceleração
Porque é que o tempo de amortecimento é importante e como é calculado?
O amortecimento correto do fim de curso é essencial para evitar danos por impacto, reduzir o ruído e prolongar a vida útil dos cilindros pneumáticos. A compreensão do tempo de amortecimento ajuda os engenheiros a conceber sistemas que equilibram o tempo de ciclo com a longevidade dos componentes.
O tempo de amortecimento em cilindros pneumáticos é calculado usando a equação t = √(2s/a), onde t é o tempo, s é o comprimento do curso de amortecimento e a é a desaceleração. Este tempo representa quanto tempo é necessário para desacelerar com segurança a massa em movimento antes do impacto, o que é crítico para evitar danos no cilindro e nos componentes ligados.

Vamos explorar os aspectos práticos dos cálculos do tempo de amortecimento e as suas implicações para a conceção do sistema.
A física por detrás do amortecimento pneumático
Amortecimento pneumático funciona através de uma compressão de ar controlada e de um escape restrito:
- Quando o pistão entra na câmara de amortecimento, o caminho de escape é restringido
- O ar retido comprime-se, criando uma contrapressão crescente
- Esta contrapressão cria uma força contrária que desacelera o pistão
- O perfil de desaceleração depende da conceção e do ajuste da almofada
Cálculo do tempo ótimo de amortecimento
O tempo de amortecimento ideal equilibra a prevenção de impactos com a eficiência do tempo de ciclo:
| Parâmetro | Fórmula | Exemplo |
|---|---|---|
| Distância de amortecimento | Com base na conceção do cilindro | 15mm (típico para furo de 40mm) |
| Desaceleração necessária | a = v²/(2s) | Para v=0,5m/s, s=15mm: a = 8,33m/s² |
| Tempo de amortecimento | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Acumulação de pressão | P = P₀(V₀/V)^γ | Depende da geometria da câmara de almofada |
Factores que afectam o desempenho do amortecimento
Vários factores influenciam o desempenho real do amortecimento:
- Design de vedação almofadado: Afecta a fuga de ar durante o amortecimento
- Ajuste da válvula de agulha: Controla a taxa de restrição dos gases de escape
- Massa em movimento: Cargas mais pesadas requerem um tempo de amortecimento mais longo
- Velocidade de aproximação: Velocidades mais elevadas exigem uma distância de almofada mais longa
- Pressão de funcionamento: Afecta a força contrária máxima disponível
Tipos de amortecimento e suas aplicações
Diferentes mecanismos de amortecimento são adequados para diferentes aplicações:
| Tipo de amortecimento | Caraterísticas | Melhores aplicações |
|---|---|---|
| Amortecimento fixo | Simples, não ajustável | Cargas leves, funcionamento consistente |
| Amortecimento ajustável | Sintonizável com válvulas de agulha | Cargas variáveis, aplicações flexíveis |
| Amortecimento auto-ajustável | Adapta-se a diferentes condições | Alteração de velocidades e cargas |
| Amortecedores externos | Elevada absorção de energia | Cargas pesadas, velocidades elevadas |
| Amortecimento eletrónico | Desaceleração controlada com precisão | Sistemas servo-pneumáticos |
Estudo de caso: Otimização do amortecimento em aplicações de ciclo elevado
Trabalhei recentemente com o Thomas, um engenheiro de projeto de um fabricante de componentes automóveis na Alemanha. A sua linha de montagem utilizava cilindros sem haste que funcionavam a 45 ciclos por minuto, mas estava a registar falhas frequentes nos vedantes e danos nos suportes de montagem.
A análise revelou que o tempo de amortecimento era demasiado curto para a massa em movimento, causando forças de impacto de quase 3G em cada fim de curso. Aumentando o curso de amortecimento de 12mm para 20mm e optimizando as definições da válvula de agulha, aumentámos o tempo de amortecimento de 0,04s para 0,07s.
Esta alteração aparentemente pequena reduziu as forças de impacto em mais de 60%, eliminou completamente os danos no suporte e prolongou a vida útil dos vedantes de 3 meses para mais de um ano - tudo isto mantendo o tempo de ciclo necessário.
Procedimento prático de regulação do amortecimento
Para um desempenho ótimo de amortecimento em cilindros sem haste:
- Arrancar com as válvulas de almofada totalmente abertas (restrição mínima)
- Fechar gradualmente a válvula de amortecimento até se obter uma desaceleração suave
- Ensaio com cargas mínimas e máximas previstas
- Verificar o desempenho do amortecimento em toda a gama de velocidades
- Ouvir os sons de impacto que indicam um amortecimento insuficiente
- Medir o tempo de desaceleração real para confirmar os cálculos
Conclusão
Compreender os princípios da cinemática do pistão - desde os requisitos de pressão para uma velocidade constante até aos limites de aceleração e aos cálculos do tempo de amortecimento - é essencial para conceber sistemas pneumáticos eficientes e fiáveis. Ao aplicar estes princípios às suas aplicações de cilindros sem haste, pode otimizar o desempenho, reduzir o consumo de energia e aumentar significativamente a vida útil dos componentes.
Perguntas frequentes sobre a cinemática do pistão em sistemas pneumáticos
De que pressão necessito para uma determinada velocidade do cilindro?
A pressão necessária depende da carga, do atrito e da área do cilindro. Calcule-a utilizando P = (F + Fr)/A, em que F é a força da carga externa, Fr é a resistência ao atrito e A é a área do pistão. Para um cilindro sem haste típico que movimenta horizontalmente uma carga de 10 kg, são necessários cerca de 1,5-2 bar para um movimento estável a velocidades moderadas.
A que velocidade pode acelerar um cilindro pneumático?
A aceleração máxima de um cilindro pneumático é calculada utilizando a = (P × A - F - Fr)/m. Os cilindros sem haste típicos podem atingir uma aceleração de 10-25 m/s², dependendo da conceção. Isto traduz-se em atingir uma velocidade de 0,5 m/s em aproximadamente 20-50 milissegundos em condições óptimas.
Que factores limitam a velocidade máxima de um cilindro sem haste?
A velocidade máxima é limitada pela capacidade do caudal da válvula, pelo volume de fornecimento de ar, pelo dimensionamento da porta, pelas capacidades de amortecimento e pela conceção do vedante. A maioria dos cilindros sem haste standard são concebidos para velocidades máximas de 0,8-1,5 m/s, embora os modelos especializados de alta velocidade possam atingir 2-3 m/s.
Como posso calcular o amortecimento adequado para a minha aplicação?
Calcule o amortecimento adequado determinando a energia cinética (KE = ½mv²) da carga em movimento e assegurando que o sistema de amortecimento pode absorver essa energia. O tempo de amortecimento deve ser calculado utilizando t = √(2s/a), em que s é a distância do amortecedor e a é a taxa de desaceleração pretendida.
O que acontece se o meu cilindro pneumático acelerar demasiado depressa?
A aceleração excessiva pode causar tensões mecânicas nos componentes de montagem, desgaste prematuro dos vedantes, aumento da vibração e do ruído, potenciais deslocações ou danos na carga e redução da precisão do sistema. Pode também levar a movimentos bruscos que afectam a qualidade do produto em aplicações de precisão.
Como é que a orientação da carga afecta a pressão necessária para o movimento?
A orientação da carga tem um impacto significativo nos requisitos de pressão. As cargas verticais que se deslocam contra a gravidade necessitam de pressão adicional para superar a força gravitacional (P = F/A + Fg/A + Fr/A). As cargas horizontais apenas necessitam de ultrapassar o atrito e a inércia. As cargas inclinadas situam-se entre estes extremos com base no seno do ângulo.
-
Fornece uma explicação fundamental da cinemática, o ramo da mecânica que descreve o movimento de objectos sem considerar as forças que causam o movimento.
sinal de entrada eletrónico, permitindo um controlo pneumático avançado. ↩ -
Detalhes da segunda lei de Newton (F=ma), o princípio fundamental da física que relaciona a força que actua sobre um objeto com a sua massa e aceleração, que é a base de todos os cálculos dinâmicos. ↩
-
Descreve a servo-pneumática, uma tecnologia de controlo avançada que combina a potência da pneumática com a precisão do controlo eletrónico em circuito fechado para obter perfis de posicionamento e movimento altamente precisos. ↩


