Está a debater-se com velocidades lentas dos cilindros, movimentos inconsistentes ou força insuficiente nos seus sistemas pneumáticos? Estes problemas comuns resultam frequentemente de uma causa mal compreendida: a resistência do fluxo. Muitos engenheiros dimensionam os seus componentes pneumáticos com base apenas nos requisitos de pressão e força, ignorando o impacto crítico da resistência ao fluxo no desempenho real.
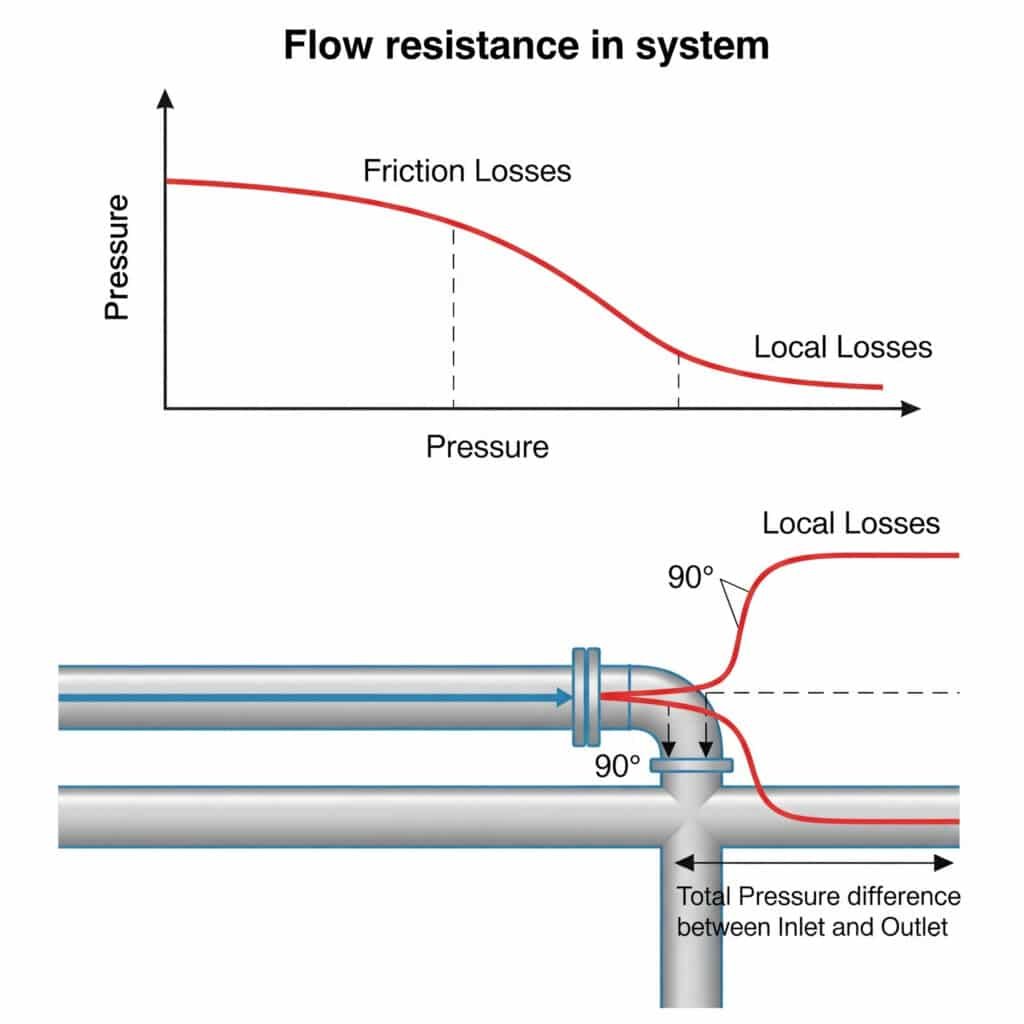
A resistência ao fluxo em sistemas pneumáticos cria quedas de pressão que reduzem a força disponível, limitam a velocidade máxima e causam movimentos inconsistentes. Esta resistência provém tanto da fricção ao longo de tubos rectos (perdas por fricção) como de perturbações em acessórios, curvas e válvulas (perdas locais). Em conjunto, estas resistências podem reduzir o desempenho real do sistema em 20-50% em comparação com os cálculos teóricos.
Nos meus mais de 15 anos na Bepto a trabalhar com sistemas pneumáticos, vi inúmeros casos em que a compreensão e o tratamento da resistência ao fluxo transformaram sistemas com baixo desempenho em operações fiáveis e eficientes. Deixem-me partilhar o que aprendi sobre como calcular e minimizar estes assassinos ocultos do desempenho.
Índice
- Como é que se calculam as perdas por fricção em linhas pneumáticas?
- Porque é que o Método do Comprimento Equivalente é fundamental para uma conceção precisa do sistema?
- O que acontece quando o ar flui através de secções de furo reduzido?
- Conclusão
- Perguntas frequentes sobre a resistência ao fluxo em sistemas pneumáticos
Como é que se calculam as perdas por fricção em linhas pneumáticas?
As perdas por fricção em tubos rectos são a base dos cálculos de resistência do fluxo, mas muitos engenheiros confiam em regras de ouro demasiado simplificadas que conduzem a sistemas subdimensionados.
As perdas por atrito em linhas pneumáticas são calculadas utilizando a Equação de Darcy-Weisbach1ΔP = λ(L/D)(ρv²/2), em que λ é o fator de atrito, L é o comprimento do tubo, D é o diâmetro do tubo, ρ é a densidade do ar e v é a velocidade do fluxo. Para sistemas pneumáticos, o fator de atrito λ varia com base em Número de Reynolds2 e a rugosidade relativa, e é normalmente determinada utilizando tabelas de pesquisa ou o Diagrama de Moody3.
Compreender as perdas por fricção tem implicações práticas na conceção do sistema e na resolução de problemas. Vou dividir isto em ideias práticas.
Utilizar eficazmente as tabelas de factores de atrito
O fator de atrito (λ) é o parâmetro chave no cálculo das quedas de pressão, mas a determinação do seu valor requer a consideração das condições de escoamento:
| Regime de caudal | Número de Reynolds (Re) | Determinação do fator de atrito |
|---|---|---|
| Fluxo laminar | Re < 2000 | λ = 64/Re |
| Fluxo de transição | 2000 < Re < 4000 | Pouco fiável - evitar conceber nesta gama |
| Fluxo turbulento | Re > 4000 | Utilizar tabelas de pesquisa baseadas na rugosidade relativa (ε/D) |
Tabela prática de pesquisa do fator de atrito
Para caudais turbulentos em sistemas pneumáticos, utilizar esta tabela simplificada:
| Material da tubagem | Rugosidade relativa (ε/D) | Fator de atrito (λ) em números de Reynolds comuns |
|---|---|---|
| Re = 10.000 | ||
| Tubos lisos (PVC, poliuretano) | 0.0001 – 0.0005 | 0.031 |
| Tubos de alumínio | 0.001 – 0.002 | 0.035 |
| Aço galvanizado | 0.003 – 0.005 | 0.042 |
| Aço enferrujado | 0.01 – 0.05 | 0.054 |
Cálculo da queda de pressão em sistemas pneumáticos reais
Vejamos um exemplo prático:
| Parâmetro | Valor/Cálculo | Exemplo |
|---|---|---|
| Diâmetro do tubo (D) | Diâmetro interno | 8mm (0,008m) |
| Comprimento do tubo (L) | Comprimento reto total | 5m |
| Caudal (Q) | Dos requisitos do sistema | 20 litros/segundo padrão |
| Densidade do ar (ρ) | À pressão de funcionamento | 7,2 kg/m³ a 6 bar |
| Velocidade do fluxo (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Número de Reynolds (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Rugosidade relativa | Para tubos de poliuretano | 0.0003 |
| Fator de fricção (λ) | Da tabela de pesquisa | 0.017 |
| Queda de pressão (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Aplicação no mundo real: Resolução de problemas de velocidade do cilindro
No ano passado, trabalhei com a Sarah, uma engenheira de fabrico de uma empresa de equipamento de embalagem no Wisconsin. O seu sistema de cilindros sem haste estava a funcionar a apenas 60% da velocidade esperada, apesar de ter o cilindro de tamanho correto e uma pressão de alimentação adequada.
Depois de analisar o seu sistema, descobri que estava a utilizar tubos de 6 mm para uma aplicação de elevado fluxo. As perdas por fricção estavam a causar uma queda de pressão de 2,1 bar, reduzindo significativamente a força e a velocidade disponíveis. Ao atualizar para tubagem de 10 mm, reduzimos a queda de pressão para 0,4 bar e o seu sistema atingiu imediatamente o desempenho necessário sem quaisquer outras alterações.
Factores que afectam as perdas por fricção em sistemas reais
Vários factores influenciam as perdas por atrito reais:
- Temperatura do ar: As temperaturas mais elevadas aumentam a viscosidade e o atrito
- Contaminação: A sujidade e o óleo podem aumentar a rugosidade efectiva
- Curvatura de tubos: A micro-deformação em tubos curvos aumenta a resistência
- Deterioração da idade: A corrosão e os depósitos aumentam a rugosidade ao longo do tempo
- Pressão de funcionamento: Pressões mais elevadas aumentam a densidade e as perdas
Porque é que o Método do Comprimento Equivalente é fundamental para uma conceção precisa do sistema?
As perdas locais em acessórios, válvulas e curvas excedem frequentemente as perdas por fricção em tubagens rectas, mas muitos engenheiros ignoram-nas ou utilizam métodos de estimativa grosseiros que conduzem a problemas de desempenho.
O método do comprimento equivalente converte as perdas locais de acessórios e válvulas num comprimento equivalente de tubo reto que causaria a mesma queda de pressão. Isto é calculado utilizando Le = K(D/λ), em que Le é o comprimento equivalente, K é o coeficiente de perda local4D é o diâmetro do tubo, e λ é o fator de atrito. Este método simplifica os cálculos e fornece previsões mais exactas do desempenho do sistema.
Vamos explorar a forma de aplicar eficazmente este método na conceção de sistemas pneumáticos.
Tabelas de comprimentos equivalentes para componentes pneumáticos comuns
Aqui está uma tabela de referência prática para componentes pneumáticos comuns:
| Componente | Valor K | Comprimento equivalente (Le/D) |
|---|---|---|
| Cotovelo de 90° (agudo) | 0.9 | 30 |
| Cotovelo de 90° (raio padrão) | 0.3 | 10 |
| Cotovelo de 45° | 0.2 | 7 |
| Junção em T (fluxo passante) | 0.3 | 10 |
| Junção em T (fluxo de ramificação) | 1.0 | 33 |
| Válvula de esfera (totalmente aberta) | 0.1 | 3 |
| Válvula de gaveta (totalmente aberta) | 0.2 | 7 |
| Acoplamento de ligação rápida | 0.4-0.8 | 13-27 |
| Válvula de retenção | 1.5-2.5 | 50-83 |
| Válvula de controlo de caudal standard | 1.0-3.0 | 33-100 |
Aplicação do método do comprimento equivalente
Para utilizar este método de forma eficaz:
- Identificar todos os componentes do seu circuito pneumático
- Determinar o valor K ou o rácio do comprimento equivalente (Le/D) para cada componente
- Calcular o comprimento equivalente multiplicando-o pelo diâmetro do tubo
- Adicionar todos os comprimentos equivalentes ao comprimento real do tubo reto
- Utilize o comprimento efetivo total nos seus cálculos de perda por atrito
Por exemplo, um sistema com 5 m de tubo reto de 8 mm mais quatro cotovelos de 90°, uma junção em T e duas ligações rápidas:
| Componente | Quantidade | Le/D | Comprimento equivalente |
|---|---|---|---|
| Cotovelos de 90° | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| Junção T | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Ligações rápidas | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Comprimento total equivalente | 0.72m | ||
| Comprimento reto real | 5.00m | ||
| Comprimento efetivo total | 5.72m |
Isto significa que o seu sistema de 5m se comporta na realidade como um sistema de 5,72m devido às perdas locais - um aumento de 14,4% no comprimento efetivo.
Estudo de caso: Otimização da colocação de válvulas em sistemas de montagem
Recentemente, ajudei o Miguel, um engenheiro de automação de uma fábrica de montagem de eletrónica no Arizona. O seu sistema de recolha e colocação estava a sofrer variações inconsistentes de movimento e de tempo de ciclo, apesar de utilizar componentes de alta qualidade.
A análise revelou que o coletor de válvulas estava localizado a 3 m de distância dos cilindros e o circuito incluía vários acessórios. O cálculo do comprimento equivalente mostrou que a sua distância real de 3m tinha um comprimento efetivo de 7,2m devido a perdas locais - mais do dobro da distância em linha reta!
Ao deslocar o coletor de válvulas para mais perto dos cilindros e ao eliminar vários acessórios, reduzimos o comprimento efetivo de 7,2 m para 2,1 m. Isto diminuiu a queda de pressão em 70%, resultando num movimento consistente e numa redução de 15% no tempo de ciclo.
Conselhos práticos para minimizar as perdas locais
Para reduzir as perdas locais nos seus sistemas pneumáticos:
- Utilizar cotovelos arredondados em vez de curvas acentuadas (reduz o valor K em 67%)
- Minimizar o número de acessórios planeando um encaminhamento mais direto
- Selecionar componentes de baixa restrição como válvulas de esfera de passagem completa, se for caso disso
- Dimensionar corretamente os acessórios - os acessórios subdimensionados causam perdas desproporcionadas
- Colocar as válvulas perto dos actuadores para minimizar o comprimento efetivo da tubagem
O que acontece quando o ar flui através de secções de furo reduzido?
As secções de diâmetro reduzido nos circuitos pneumáticos - tais como válvulas parcialmente fechadas, acessórios subdimensionados ou transições de diâmetro - criam restrições de fluxo significativas que podem afetar gravemente o desempenho do sistema.
Quando o ar passa através de secções de furo reduzido, quedas de pressão5 ocorrem de acordo com a fórmula ΔP = ρ(v₂² - v₁²)/2, onde v₁ é a velocidade antes da restrição e v₂ é a velocidade na restrição. Isto pode ser compensado utilizando o fator de compensação da relação de furo C = (1 - (d/D)⁴), em que d é o diâmetro reduzido e D é o diâmetro original. Este fator ajuda a prever o desempenho real do sistema e a evitar o subdimensionamento de componentes.
Vamos explorar as implicações práticas das secções de furo reduzido e a forma de as ter em conta na conceção do sistema.
Cálculo de quedas de pressão em transições de diâmetro
Quando o ar passa de um diâmetro maior para um diâmetro menor, a queda de pressão pode ser calculada utilizando
| Parâmetro | Fórmula | Exemplo |
|---|---|---|
| Diâmetro original (D) | De especificações | 10 mm |
| Diâmetro reduzido (d) | De especificações | 6mm |
| Relação de furos (d/D) | Divisão simples | 0.6 |
| Caudal (Q) | Dos requisitos do sistema | 15 litros/segundo padrão |
| Velocidade no tubo original (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Velocidade na secção reduzida (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Queda de pressão (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Fator de compensação (C) | C = (1 - (d/D)⁴) | 0.87 |
Cenários comuns de redução de furos e o seu impacto
Eis como as diferentes reduções de furo afectam a capacidade de fluxo:
| Redução de furos | Redução da capacidade de fluxo | Aumento da queda de pressão |
|---|---|---|
| 10mm a 8mm | 36% | 2.4× |
| 10mm a 6mm | 64% | 7.7× |
| 10mm a 4mm | 84% | 39× |
| 8mm a 6mm | 44% | 3.2× |
| 8mm a 4mm | 75% | 16× |
| 6mm a 4mm | 56% | 5.1× |
Estes números mostram porque é que reduções aparentemente pequenas no diâmetro podem ter efeitos dramáticos no desempenho do sistema.
O efeito cumulativo de restrições múltiplas
Nos circuitos pneumáticos reais, ocorrem várias restrições em série. O seu efeito é cumulativo e pode ser calculado utilizando:
- Converter cada restrição no seu fator C equivalente
- Calcular o fator C total: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Utilize este fator total para determinar a redução global do desempenho do sistema
Estudo de caso: Resolução de problemas de incompatibilidade entre válvula e atuador
No mês passado, trabalhei com o Thomas, um supervisor de manutenção numa fábrica de mobiliário na Carolina do Norte. O seu novo sistema de cilindros sem haste estava a funcionar a menos de metade da velocidade esperada, apesar de utilizar o tamanho de válvula recomendado pelo fabricante.
A investigação revelou múltiplas reduções de furos no seu circuito:
- Linha de alimentação de 10 mm para orifícios de válvula de 8 mm (C₁ = 0,36)
- Orifícios de válvula de 8 mm para acessórios de 6 mm (C₂ = 0,44)
- Acessórios de 6 mm para orifícios de cilindro de 8 mm com restrições internas (C₃ = 0,32)
O fator de compensação total era Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, o que significa que o sistema estava a perder 75% da sua capacidade de fluxo teórica!
Ao atualizar para componentes adequadamente dimensionados em todo o sistema, eliminámos estas restrições e atingimos o desempenho necessário sem alterar o cilindro ou a pressão de alimentação.
Estratégias práticas para minimizar as perdas de redução de furos
Reduzir as perdas resultantes de reduções de furos:
- Dimensionar os componentes de forma coerente em todo o circuito pneumático
- Utilizar o maior tamanho de tubo possível para aplicações de caudal elevado
- Prestar atenção às restrições dos componentes internose não apenas tamanhos de ligação
- Considerar trajectórias de fluxo paralelas para requisitos de caudal elevado
- Eliminar adaptadores e transições desnecessários sempre que possível
O princípio do "elo mais fraco" nos sistemas pneumáticos
Lembre-se de que o desempenho do seu sistema pneumático é limitado pelo seu componente mais restritivo. Um único elemento subdimensionado pode anular os benefícios de componentes adequadamente dimensionados em outras partes do sistema.
Por exemplo, um sistema com tubagem de 10 mm, válvulas de 10 mm, mas acessórios de 6 mm no cilindro terá essencialmente o mesmo desempenho que um sistema com componentes de 6 mm em toda a sua extensão - a um custo mais elevado.
Conclusão
Compreender e calcular corretamente a resistência ao fluxo - através de tabelas de factores de fricção, métodos de comprimento equivalente e compensação de furo reduzido - é essencial para projetar sistemas pneumáticos que tenham o desempenho esperado em condições reais. Ao aplicar estes métodos de cálculo e princípios de conceção, pode otimizar as suas aplicações de cilindros sem haste e outros sistemas pneumáticos para obter o máximo desempenho e fiabilidade.
Perguntas frequentes sobre a resistência ao fluxo em sistemas pneumáticos
Qual é a queda de pressão aceitável num sistema pneumático?
A queda de pressão aceitável depende dos requisitos da sua aplicação, mas como diretriz geral, limite a queda de pressão total a 10-15% da pressão de alimentação para um funcionamento eficiente. Para um sistema de 6 bar, isto significa manter a queda de pressão total abaixo de 0,6-0,9 bar. As aplicações críticas podem exigir quedas de pressão ainda mais baixas, de 5-8%, para manter um desempenho consistente.
Qual é a relação entre o diâmetro do tubo e a queda de pressão?
A queda de pressão é inversamente proporcional à quinta potência do diâmetro (D⁵) para o fluxo turbulento em sistemas pneumáticos. Isto significa que duplicar o diâmetro do tubo reduz a queda de pressão em aproximadamente 32 vezes. Por exemplo, aumentar a tubagem de 6 mm para 12 mm pode reduzir a queda de pressão de 1,5 bar para apenas 0,047 bar sob as mesmas condições de fluxo.
Como é que determino o tamanho correto do tubo para a minha aplicação pneumática?
Selecione o tamanho do tubo com base nos requisitos de caudal e na queda de pressão aceitável. Calcule o número de Reynolds e o fator de atrito e, em seguida, use a equação de Darcy-Weisbach para determinar a queda de pressão para diferentes diâmetros. Escolha o menor diâmetro que mantenha a queda de pressão dentro dos limites aceitáveis (tipicamente <10% da pressão de alimentação) enquanto considera as restrições de espaço e custo.
O que cria mais restrições: um cotovelo de 90° ou 5 metros de tubo reto?
Um cotovelo agudo de 90° cria normalmente uma resistência equivalente a 30 diâmetros de tubo reto. Para tubos de 8 mm, um cotovelo agudo equivale a aproximadamente 240 mm (30 × 8 mm) de tubo reto. Isso significa que 5 metros de tubo reto criam cerca de 21 vezes mais restrição do que um único cotovelo. No entanto, os sistemas contêm frequentemente vários cotovelos e acessórios, cujo efeito cumulativo pode exceder as perdas de comprimento reto.
Como é que os acessórios de ligação rápida afectam o desempenho do sistema?
Os acessórios de ligação rápida padrão introduzem normalmente uma perda local equivalente a 15-25 diâmetros de tubo reto. Mais significativamente, muitas conexões rápidas têm restrições internas menores do que o seu tamanho nominal. Uma conexão rápida de "10mm" pode ter uma restrição interna de apenas 7-8mm, criando uma redução de diâmetro que pode reduzir a capacidade de fluxo em 50-70% nesse ponto.
Qual é o impacto das válvulas de controlo de fluxo parcialmente fechadas no desempenho do sistema?
Uma válvula de controlo de caudal fechada a 50% da sua área de passagem total não reduz o caudal em apenas 50% - reduz o caudal em aproximadamente 75% devido à relação não linear entre o diâmetro e a capacidade de caudal. A queda de pressão aumenta de acordo com o quadrado da variação da velocidade, pelo que reduzir para metade o diâmetro efetivo aumenta a queda de pressão em cerca de 16 vezes nas mesmas condições de caudal.
-
Fornece uma análise detalhada da equação de Darcy-Weisbach, uma fórmula fundamental e amplamente utilizada na dinâmica dos fluidos para calcular a perda de pressão devido ao atrito numa tubagem. ↩
-
Oferece uma definição clara do número de Reynolds, uma quantidade crítica sem dimensão utilizada para prever padrões de fluxo (laminar ou turbulento) em diferentes situações de fluxo de fluidos. ↩
-
Apresenta o diagrama de Moody, um gráfico abrangente que representa o fator de atrito de Darcy em função do número de Reynolds e da rugosidade relativa, que é a ferramenta padrão para os engenheiros determinarem a queda de pressão nas tubagens. ↩
-
Explica o conceito do valor K, ou coeficiente de perda local, um número sem dimensão utilizado para caraterizar a perda de pressão num encaixe de tubagem ou válvula como parte do método do comprimento equivalente. ↩
-
Apresenta em pormenor a física subjacente à queda de pressão que ocorre quando um fluido passa através de uma restrição (um orifício), com base nos princípios da equação da continuidade e do princípio de Bernoulli. ↩



