O pesadelo de qualquer engenheiro de manutenção é a falha inesperada do equipamento. Quando as máquinas vibram na sua frequência natural, podem ocorrer danos catastróficos em poucos minutos. Já vi este problema custar às empresas milhares de euros em tempo de inatividade.
Ressonância de vibração1 ocorre quando uma força externa coincide com a frequência natural de um sistema, causando oscilações amplificadas que podem danificar o equipamento. Compreender e controlar este fenómeno é essencial para evitar falhas e prolongar a vida útil das máquinas.
Deixem-me partilhar uma história rápida. No ano passado, um cliente da Alemanha telefonou-me em pânico. A sua linha de produção tinha parado porque um cilindro sem haste estava a vibrar violentamente. O problema? Ressonância. No final deste artigo, saberá como identificar e evitar problemas semelhantes nos seus sistemas.
Índice
- Fórmula de frequência natural: Como pode calcular os pontos vulneráveis do seu sistema?
- Modelo massa-mola: Porque é que esta abordagem simplificada é tão valiosa?
- Otimização do rácio de amortecimento: Que experiências produzem os melhores resultados?
- Conclusão
- Perguntas frequentes sobre a ressonância de vibrações
Fórmula de frequência natural: Como pode calcular os pontos vulneráveis do seu sistema?
Compreender a frequência natural do seu equipamento é o primeiro passo para evitar problemas de ressonância. Este valor crítico determina quando é que o seu sistema é mais vulnerável a problemas de vibração.
O frequência natural2 (fn) de um sistema pode ser calculada usando a fórmula: fn = (1/2π) × √(k/m), onde k é o coeficiente de rigidez e m é a massa. Este cálculo revela a frequência com que o sistema entrará em ressonância se for excitado por forças externas correspondentes.
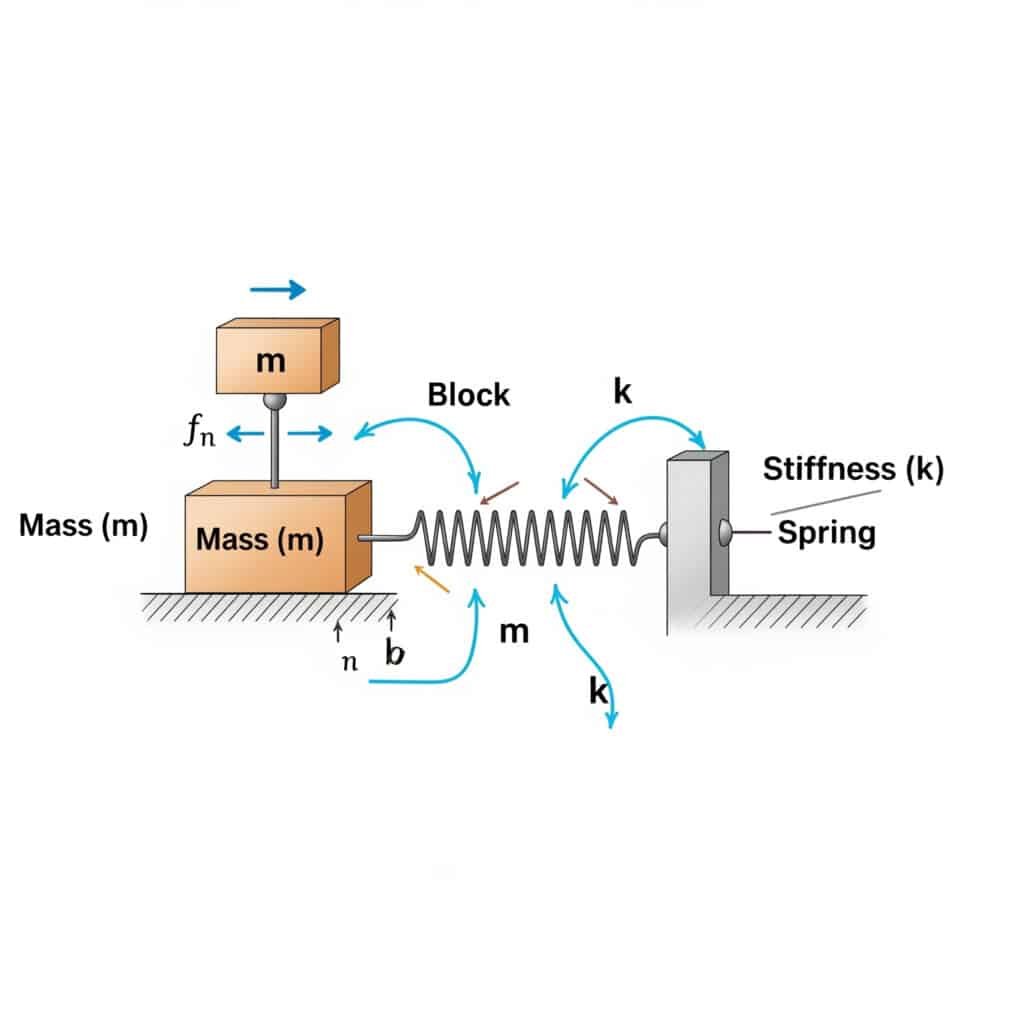
Quando visitei uma fábrica na Suíça, reparei que os seus cilindros pneumáticos sem haste estavam a falhar prematuramente. A sua equipa de manutenção não tinha calculado a frequência natural da sua instalação. Depois de aplicar esta fórmula, identificámos que a sua velocidade de funcionamento estava perigosamente próxima da frequência natural do sistema.
Aplicações práticas do cálculo de frequências naturais
A fórmula da frequência natural não é apenas teórica - tem aplicações diretas em vários contextos industriais:
- Seleção de equipamento: Escolha de componentes com frequências naturais distantes das suas condições de funcionamento
- Manutenção preventiva: Programação de inspecções com base em perfis de risco de vibração
- Resolução de problemas: Identificar a causa das vibrações inesperadas
Valores de frequência natural comuns para componentes industriais
| Componente | Gama de frequências naturais típicas (Hz) |
|---|---|
| Cilindros sem haste | 10-50 Hz |
| Suportes de montagem | 20-100 Hz |
| Estruturas de apoio | 5-30 Hz |
| Válvulas de controlo | 40-200 Hz |
Factores críticos que afectam a frequência natural
O cálculo da frequência natural parece simples, mas vários factores podem complicar as aplicações no mundo real:
- Distribuição não uniforme da massa: A maioria dos componentes industriais não tem uma massa perfeitamente distribuída
- Rigidez variável: Os componentes podem ter rigidez diferente em diferentes direcções
- Pontos de ligação: A forma como os componentes são montados afecta significativamente as suas caraterísticas de vibração
- Efeitos da temperatura: As propriedades de massa e de rigidez podem alterar-se com a temperatura
Modelo massa-mola: Porque é que esta abordagem simplificada é tão valiosa?
O modelo massa-mola fornece uma estrutura intuitiva para a compreensão de sistemas de vibração complexos. Reduz máquinas complicadas a elementos básicos que os engenheiros podem analisar facilmente.
O modelo massa-mola3 simplifica a análise de vibrações ao representar sistemas mecânicos como massas discretas ligadas por molas. Esta abordagem permite aos engenheiros prever o comportamento do sistema, identificar potenciais problemas de ressonância e desenvolver soluções eficazes sem matemática complexa.
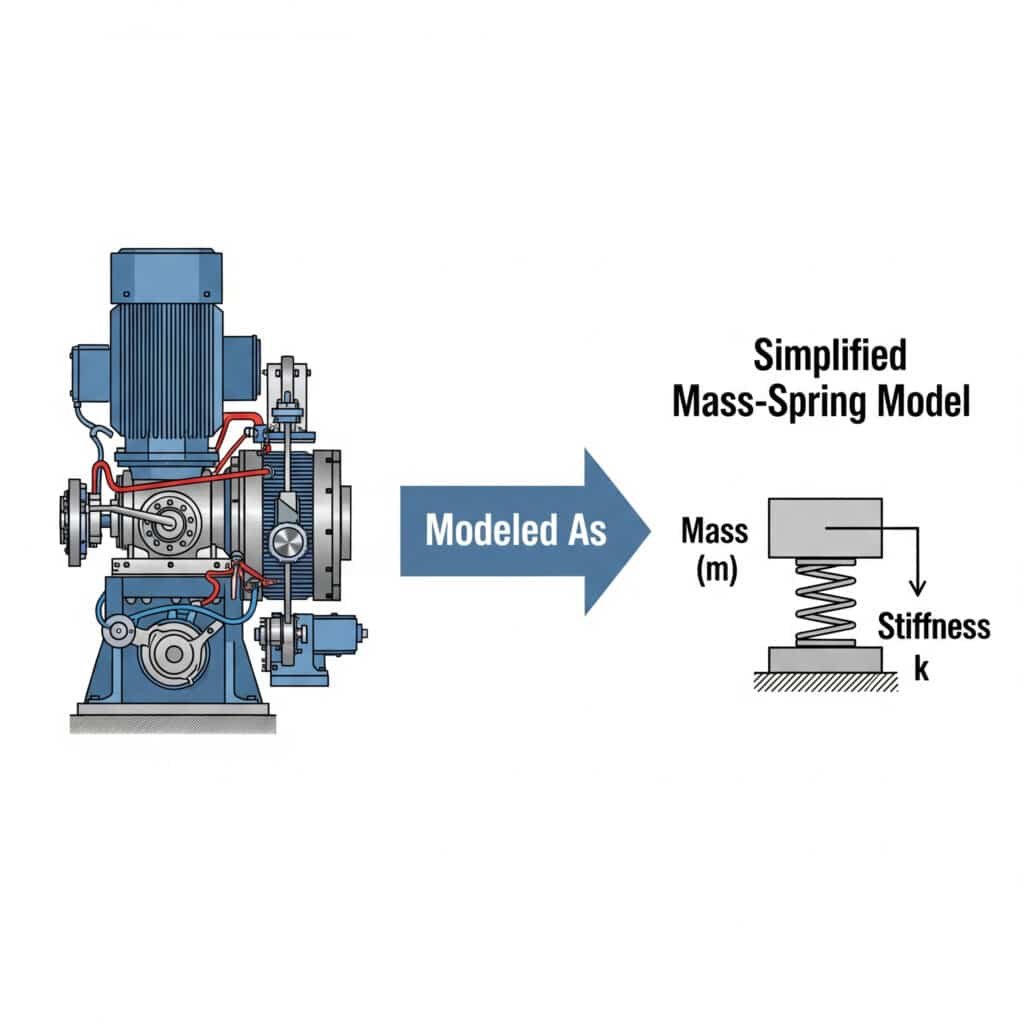
Lembro-me de trabalhar com um fabricante de peças para automóveis no Michigan que não conseguia perceber porque é que os seus cilindros guiados sem haste estavam a falhar. Ao modelar o seu sistema como um simples arranjo massa-mola, identificámos que os suportes de montagem estavam a atuar como molas não intencionais, criando uma condição de ressonância.
Conversão de sistemas reais em modelos de massa-mola
Para aplicar esta abordagem ao seu equipamento:
- Identificar as principais massas: Determinar quais os componentes que contribuem com um peso significativo
- Localizar os elementos de mola: Encontrar componentes que armazenem e libertem energia (molas reais, suportes flexíveis, etc.)
- Ligações do mapa: Documentar a forma como as massas e as molas interagem
- Simplificar: Combinar elementos semelhantes para criar um modelo gerível
Tipos de sistemas de molas de massa
| Tipo de sistema | Descrição | Aplicações comuns |
|---|---|---|
| DOF único | Uma massa com uma mola | Cilindros pneumáticos simples |
| Multi-DOF | Massas múltiplas com molas múltiplas | Máquinas complexas com vários componentes |
| Contínuo | DOF infinito (requer uma análise diferente) | Vigas, placas e cascas |
Considerações sobre modelação avançada
Embora o modelo básico massa-mola seja valioso, várias melhorias tornam-no mais realista:
- Adição de amortecedores: Os sistemas reais têm sempre dissipação de energia
- Considerando as não linearidades: As molas nem sempre seguem Lei de Hooke4 perfeitamente
- Contabilização das vibrações forçadas: As forças externas alteram o comportamento do sistema
- Incluindo efeitos de acoplamento: O movimento numa direção pode afetar outras direcções
Otimização do rácio de amortecimento: Que experiências produzem os melhores resultados?
O amortecimento é a sua melhor defesa contra problemas de ressonância. Encontrar o rácio de amortecimento ideal através da experimentação pode melhorar drasticamente o desempenho e a fiabilidade do sistema.
Rácio de amortecimento5 As experiências de otimização envolvem o teste sistemático de diferentes configurações de amortecimento para encontrar o equilíbrio ideal entre o controlo das vibrações e a capacidade de resposta do sistema. O rácio de amortecimento ideal situa-se normalmente entre 0,2 e 0,7, proporcionando uma supressão suficiente das vibrações sem perda excessiva de energia.
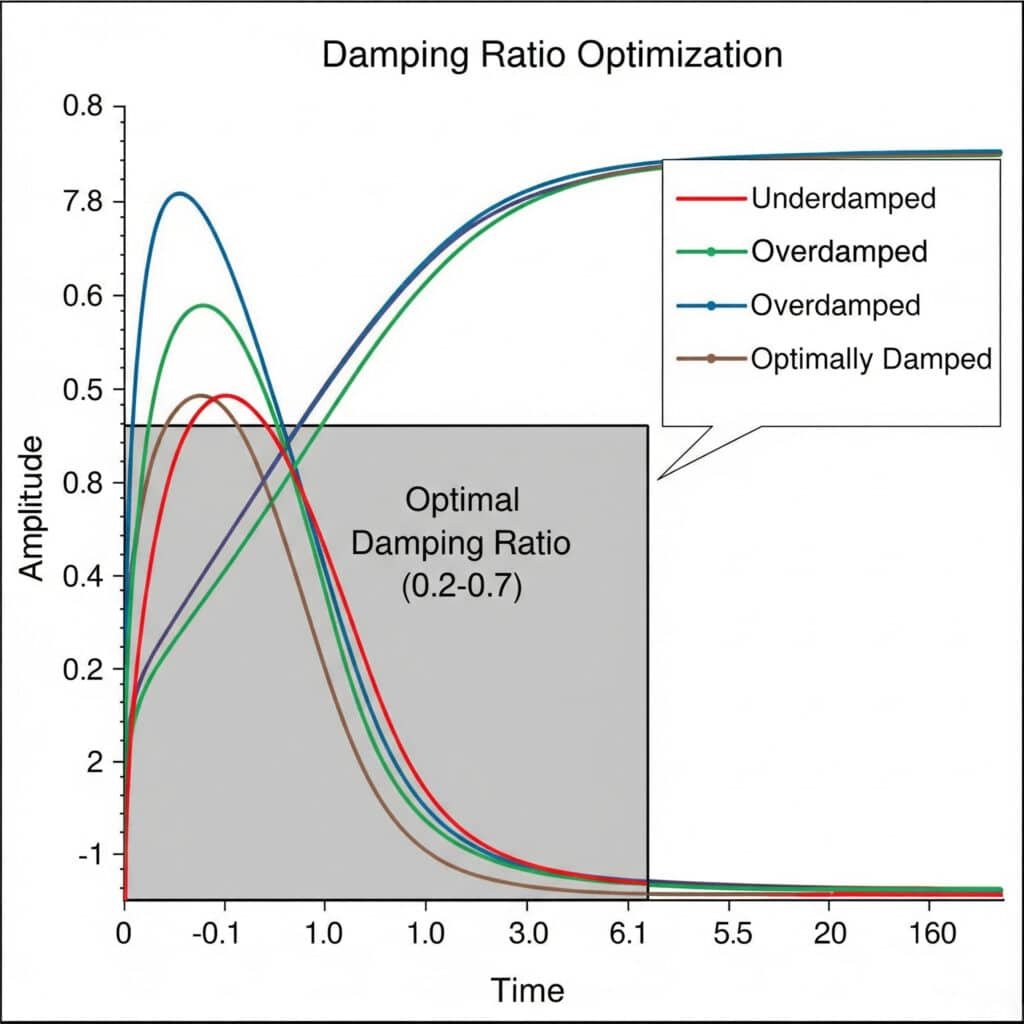
No mês passado, ajudei um fabricante de equipamento de processamento alimentar em França a resolver problemas de vibração persistentes nos seus cilindros magnéticos sem haste. Através de uma série de experiências de rácio de amortecimento, descobrimos que a sua conceção original tinha um rácio de amortecimento de apenas 0,05 - demasiado baixo para evitar problemas de ressonância.
Configuração experimental para o ensaio do rácio de amortecimento
Realizar experiências de otimização do amortecimento eficaz:
- Medição de base: Registar a resposta do sistema sem amortecimento adicional
- Testes incrementais: Adicionar elementos de amortecimento em incrementos controlados
- Medição da resposta: Medir a amplitude, o tempo de estabilização e a resposta em frequência
- Análise de dados: Calcular o rácio de amortecimento para cada configuração
- Validação: Verificar o desempenho em condições reais de funcionamento
Comparação de tecnologias de amortecimento
| Tecnologia de amortecimento | Vantagens | Limitações | Aplicações típicas |
|---|---|---|---|
| Amortecedores viscosos | Desempenho previsível, temperatura estável | Necessidade de manutenção, potenciais fugas | Máquinas pesadas, equipamentos de precisão |
| Amortecedores de fricção | Design simples, económico | Desgaste ao longo do tempo, comportamento não linear | Suportes estruturais, máquinas de base |
| Amortecimento de materiais | Sem partes móveis, compacto | Gama de regulação limitada | Instrumentos de precisão, isolamento de vibrações |
| Amortecimento ativo | Adaptável a condições variáveis | Complexo, requer energia | Aplicações críticas, equipamentos de velocidade variável |
Otimização do amortecimento para diferentes condições de funcionamento
A relação de amortecimento ideal não é universal - depende da sua aplicação específica:
- Operações de alta velocidade: Os rácios de amortecimento mais baixos (0,1-0,3) mantêm a capacidade de resposta
- Aplicações de precisão: Os rácios de amortecimento mais elevados (0,5-0,7) proporcionam estabilidade
- Sistemas de carga variável: Pode ser necessário um amortecimento adaptativo
- Ambientes sensíveis à temperatura: Considerar materiais de amortecimento com propriedades estáveis
Estudo de caso: Otimização do Amortecimento do Cilindro sem Haste
Ao otimizar um cilindro sem haste de duplo efeito para uma máquina de embalagem, testámos cinco configurações de amortecimento diferentes:
- Almofadas de extremidade standard: Rácio de amortecimento = 0,12
- Almofadas alargadas: Rácio de amortecimento = 0,25
- Amortecedores externos: Rácio de amortecimento = 0,41
- Suportes de montagem em material compósito: Rácio de amortecimento = 0,38
- Abordagem combinada (3+4): Rácio de amortecimento = 0,53
A abordagem combinada proporcionou o melhor desempenho, reduzindo a amplitude de vibração em 78% e mantendo tempos de resposta aceitáveis.
Conclusão
Compreender a ressonância de vibração através de cálculos de frequência natural, modelação massa-mola e otimização do rácio de amortecimento é crucial para evitar falhas no equipamento. Ao aplicar estes princípios, pode prolongar a vida útil das máquinas, reduzir o tempo de inatividade e melhorar o desempenho geral do sistema.
Perguntas frequentes sobre a ressonância de vibrações
O que é a ressonância de vibrações em equipamentos industriais?
A ressonância de vibração ocorre quando uma força externa coincide com a frequência natural de um sistema, causando oscilações amplificadas. No equipamento industrial, este fenómeno pode conduzir a movimentos excessivos, fadiga dos componentes e falhas catastróficas se não for gerido corretamente.
Como posso identificar se o meu sistema está a sofrer ressonância?
Procure sintomas como aumentos inexplicáveis de ruído, vibração visível a velocidades específicas, falhas prematuras de componentes e degradação do desempenho que ocorre em pontos de funcionamento consistentes. As ferramentas de análise de vibrações podem confirmar as condições de ressonância.
Qual é a diferença entre vibração forçada e ressonância?
A vibração forçada ocorre sempre que uma força externa actua sobre um sistema, enquanto a ressonância é a condição específica em que essa frequência forçada coincide com a frequência natural do sistema, resultando numa resposta amplificada. Toda a ressonância envolve vibração forçada, mas nem toda a vibração forçada causa ressonância.
Como é que a conceção de um cilindro pneumático sem haste afecta as suas caraterísticas de vibração?
A conceção de cilindros pneumáticos sem haste - com o seu carro móvel, sistema de vedação interno e mecanismos de guia - cria desafios de vibração únicos. O perfil estendido actua como uma viga que pode fletir, a massa do carro cria forças de inércia e as bandas de vedação podem introduzir fricção variável.
Que modificações simples podem reduzir a ressonância no equipamento existente?
Para o equipamento existente com problemas de ressonância, considere adicionar massa para alterar a frequência natural, instalar amortecedores externos ou amortecedores, modificar os métodos de montagem para incluir o isolamento de vibrações ou ajustar as velocidades de funcionamento para evitar frequências de ressonância.
-
Fornece uma explicação fundamental da ressonância mecânica, frequentemente com exemplos visuais, demonstrando como uma pequena força periódica pode produzir oscilações de grande amplitude num sistema. ↩
-
Oferece uma visão detalhada da física da frequência natural, a frequência específica à qual um sistema tende a oscilar na ausência de qualquer força motriz ou de amortecimento. ↩
-
Explica os princípios do modelo massa-mola, uma idealização fundamental em física e engenharia utilizada para analisar sistemas complexos que exibem movimento harmónico simples. ↩
-
Detalhes A Lei de Hooke, um princípio da física que afirma que a força necessária para estender ou comprimir uma mola por uma certa distância é diretamente proporcional a essa distância. ↩
-
Descreve o rácio de amortecimento, uma medida sem dimensão que define a forma como as oscilações num sistema decaem após uma perturbação, o que é fundamental para controlar a ressonância. ↩


