
Já alguma vez tocaste num cilindro pneumático depois de um funcionamento contínuo e ficou surpreendido com a sensação de calor? Esse calor não é apenas um inconveniente - representa energia desperdiçada, eficiência reduzida e potenciais problemas de fiabilidade que podem estar a custar milhares à sua empresa.
A transferência de calor em sistemas pneumáticos ocorre através de três mecanismos: condução através dos materiais dos componentes, convecção entre as superfícies e o ar, e radiação das superfícies quentes. A compreensão e otimização destes princípios podem reduzir as temperaturas de funcionamento em 15-30%, prolongar a vida útil dos componentes até 40% e melhorar a eficiência energética em 5-15%.
No mês passado, prestei consultoria a uma fábrica de processamento de alimentos na Geórgia, onde os seus cilindros sem haste estavam a falhar a cada 3-4 meses devido a problemas térmicos. A sua equipa de manutenção estava simplesmente a substituir componentes sem abordar a causa principal. Aplicando princípios de transferência de calor adequados, reduzimos as temperaturas de funcionamento em 22°C e aumentámos a vida útil dos componentes para mais de um ano. Deixe-me mostrar-lhe como o fizemos - e como pode aplicar estes mesmos princípios aos seus sistemas.
Índice
- Cálculo do coeficiente de condução: Como é que o calor se move através dos seus componentes?
- Métodos de Melhoria da Convecção: Que técnicas maximizam a transferência de calor ar-superfície?
- Modelo de eficiência de radiação: Quando é que a radiação térmica é importante nos sistemas pneumáticos?
- Conclusão
- Perguntas frequentes sobre a transferência de calor em sistemas pneumáticos
Cálculo do coeficiente de condução: Como é que o calor se move através dos seus componentes?
A condução é o principal mecanismo de transferência de calor em componentes pneumáticos sólidos. Compreender como calcular e otimizar os coeficientes de condução é essencial para gerir as temperaturas do sistema.
O coeficiente de condução de calor pode ser calculado utilizando Lei de Fourier1q = -k(dT/dx), em que q é o fluxo de calor (W/m²), k é a condutividade térmica (W/m-K) e dT/dx é o gradiente de temperatura. Para os componentes pneumáticos, a condução efectiva depende da seleção do material, da qualidade da interface e de factores geométricos que afectam o comprimento do caminho do calor e a área da secção transversal.
Lembro-me de ter resolvido problemas numa linha de produção no Tennessee em que os rolamentos dos cilindros sem haste estavam a falhar prematuramente. A equipa de manutenção tinha experimentado vários lubrificantes sem sucesso. Quando analisámos os caminhos de condução, descobrimos um estrangulamento térmico na interface rolamento-caixa. Melhorando o acabamento da superfície e aplicando um composto termicamente condutor, aumentámos o coeficiente de condução efetivo em 340% e eliminámos completamente as falhas.
Equações fundamentais de condução
Vamos analisar as principais equações para calcular a condução em componentes pneumáticos:
Lei de Fourier para a condução de calor
A equação básica que rege a condução de calor é:
q = -k(dT/dx)
Onde:
- q = Fluxo de calor (W/m²)
- k = Condutividade térmica (W/m-K)
- dT/dx = Gradiente de temperatura (K/m)
Para um caso unidimensional simples com secção transversal constante:
Q = kA(T₁-T₂)/L
Onde:
- Q = Taxa de transferência de calor (W)
- A = Área da secção transversal (m²)
- T₁, T₂ = Temperaturas em cada extremidade (K)
- L = Comprimento do trajeto do calor (m)
Conceito de resistência térmica
Para geometrias complexas, a abordagem da resistência térmica é frequentemente mais prática:
R = L/(kA)
Onde:
- R = Resistência térmica (K/W)
Para sistemas com vários componentes em série:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
E a taxa de transferência de calor torna-se:
Q = ΔT/Rtotal
Comparação da condutividade térmica dos materiais
| Material | Condutividade térmica (W/m-K) | Condutividade relativa | Aplicações comuns |
|---|---|---|---|
| Alumínio | 205-250 | Elevado | Cilindros, dissipadores de calor |
| Aço | 36-54 | Médio | Componentes estruturais |
| Aço inoxidável | 14-16 | Baixo-Médio | Ambientes corrosivos |
| Bronze | 26-50 | Médio | Rolamentos, casquilhos |
| PTFE | 0.25 | Muito baixo | Vedantes, rolamentos |
| Borracha nitrílica | 0.13 | Muito baixo | O-rings, vedantes |
| Ar (parado) | 0.026 | Extremamente baixo | Preenchimento de lacunas |
| Pasta térmica | 3-8 | Baixa | Material da interface |
Resistência de contacto em conjuntos pneumáticos
Nas interfaces entre componentes, a resistência de contacto afecta significativamente a transferência de calor:
Rcontacto = 1/(hc × A)
Onde:
- hc = Coeficiente de contacto (W/m²-K)
- A = Área de contacto (m²)
Os factores que afectam a resistência de contacto incluem:
- Rugosidade da superfície: As superfícies mais rugosas têm menos área de contacto real
- Pressão de contacto: Uma pressão mais elevada aumenta a área de contacto efectiva
- Materiais de interface: Os compostos térmicos preenchem as lacunas de ar
- Limpeza da superfície: Os contaminantes podem aumentar a resistência
Estudo de caso: Otimização Térmica de Cilindros sem Haste
Para um cilindro magnético sem haste com problemas térmicos:
| Componente | Desenho original | Design optimizado | Melhoria |
|---|---|---|---|
| Corpo do cilindro | Alumínio anodizado | Mesmo material, acabamento melhorado | 15% melhor condução |
| Interface do rolamento | Contacto metal-metal | Composto térmico adicionado | 340% melhor condução |
| Suportes de montagem | Aço pintado | Alumínio nu | 280% melhor condução |
| Resistência térmica global | 2,8 K/W | 0,7 K/W | Redução 75% |
| Temperatura de funcionamento | 78°C | 56°C | Redução de 22°C |
| Vida útil do componente | 4 meses | >12 meses | Melhoria de 3× |
Técnicas práticas de otimização da condução
Com base na minha experiência com centenas de sistemas pneumáticos, eis as abordagens mais eficazes para melhorar a condução:
Otimização da interface
- Acabamento de superfícies: Melhorar a suavidade da superfície de contacto para Ra 0,4-0,8 μm
- Materiais de interface térmica2: Aplicar compostos adequados (3-8 W/m-K)
- Torque do fixador: Assegurar um aperto correto para uma pressão de contacto ideal
- Limpeza: Remover todos os óleos e contaminantes antes da montagem
Estratégias de seleção de materiais
- Caminhos críticos de calor: Utilizar materiais de alta condutividade (alumínio, cobre)
- Interrupções térmicas: Utilizar intencionalmente materiais de baixa condutividade para isolar o calor
- Abordagens compostas: Combinar materiais para otimizar o desempenho/custo
- Materiais anisotrópicos: Utilizar a condutividade direcional quando apropriado
Otimização Geométrica
- Comprimento do percurso de calor: Minimizar a distância entre as fontes e os dissipadores de calor
- Área de secção transversal: Maximizar a área perpendicular ao fluxo de calor
- Estrangulamentos térmicos: Identificar e eliminar constrições no percurso do calor
- Caminhos redundantes: Criar várias vias de condução paralelas
Métodos de Melhoria da Convecção: Que técnicas maximizam a transferência de calor ar-superfície?
A convecção é frequentemente o fator limitante no arrefecimento de sistemas pneumáticos. O aumento da transferência de calor por convecção pode melhorar drasticamente a gestão térmica e o desempenho do sistema.
A transferência de calor por convecção é a seguinte Lei de Newton do arrefecimento3: Q = hA(Ts-T∞), onde h é o coeficiente de convecção (W/m²-K), A é a área da superfície, e (Ts-T∞) é a diferença de temperatura entre a superfície e o fluido. Os métodos de melhoramento incluem o aumento da área da superfície através de alhetas, a melhoria da velocidade do fluido com fluxo de ar direcionado e a otimização das caraterísticas da superfície para promover camadas limite turbulentas.
Durante uma auditoria de eficiência energética numa fábrica de embalagens no Arizona, deparei-me com um sistema pneumático a funcionar num ambiente de 43°C. Os seus cilindros sem haste estavam a sobreaquecer, apesar de cumprirem todos os requisitos de manutenção. Ao implementar uma melhoria de convecção direcionada - adicionando pequenas aletas de alumínio e uma ventoinha de baixo consumo - aumentámos o coeficiente de convecção em 450%. Isto reduziu as temperaturas de funcionamento de níveis perigosos para níveis dentro das especificações, sem grandes modificações no sistema.
Fundamentos da transferência de calor por convecção
A equação básica que rege a transferência de calor por convecção é:
Q = hA(Ts-T∞)
Onde:
- Q = Taxa de transferência de calor (W)
- h = Coeficiente de convecção (W/m²-K)
- A = Área de superfície (m²)
- Ts = Temperatura da superfície (K)
- T∞ = Temperatura do fluido (ar) (K)
O coeficiente de convecção h depende de vários factores:
- Propriedades dos fluidos (densidade, viscosidade, condutividade térmica)
- Caraterísticas do escoamento (velocidade, turbulência)
- Geometria e orientação da superfície
- Regime de escoamento (convecção natural vs. forçada)
Convecção natural vs. forçada
| Parâmetro | Convecção natural | Convecção forçada | Implicações |
|---|---|---|---|
| Valor h típico | 5-25 W/m²-K | 25-250 W/m²-K | A convecção forçada pode ser 10 vezes mais eficaz |
| Força motriz | Flutuabilidade (diferença de temperatura) | Pressão externa (ventiladores, sopradores) | A convecção forçada é menos dependente da temperatura |
| Padrão de fluxo | Fluxo vertical ao longo de superfícies | Direcional com base no mecanismo forçador | O fluxo forçado pode ser optimizado para componentes específicos |
| Fiabilidade | Passivo, sempre presente | Necessita de energia e manutenção | A convecção natural proporciona um arrefecimento de base |
| Requisitos de espaço | Necessita de espaço livre para circulação de ar | Necessita de espaço para ventiladores e condutas de ar | Os sistemas forçados necessitam de mais planeamento |
Técnicas de melhoramento da convecção
Aumento da área de superfície
Aumento da área de superfície efectiva através de:
Barbatanas e superfícies alargadas
- Barbatanas de pinos: Fluxo de ar omnidirecional, aumento da área 150-300%
- Aletas de placa: Fluxo de ar direcional, aumento da área 200-500%
- Superfícies onduladas: Melhoria moderada, aumento da área 50-150%Desbaste de superfícies
- Micro-texturas: Aumento da área efectiva de 5-15%
- Superfícies com covinhas: aumento de 10-30% mais efeitos da camada limite
- Padrões ranhurados: 15-40% aumentam com benefícios direcionais
Manipulação de fluxos
Melhoria das caraterísticas do fluxo de ar através de:
Sistemas de ar forçado
- Ventiladores: fluxo de ar direcional, 200-600% h melhoria
- Sopradores: Fluxo de alta pressão, 300-800% h melhoria
- Jactos de ar comprimido: Arrefecimento direcionado, 400-1000% melhoria local hOtimização do percurso do fluxo
- Deflectores: Ar direto para componentes críticos
- Efeitos Venturi: Acelerar o ar sobre superfícies específicas
- Geradores de vórtices: Criam turbulência para perturbação da camada limite
Modificações de superfície
Alteração das propriedades da superfície para melhorar a convecção:
Tratamentos de Emissividade
- Óxido preto: Aumenta a emissividade para 0,7-0,9
- Anodização: Emissividade controlada de 0,4-0,9
- Tintas e revestimentos: Emissividade personalizável até 0,98Controlo da molhabilidade
- Revestimentos hidrofílicos: Melhoram o arrefecimento líquido
- Superfícies hidrofóbicas: Evitam problemas de condensação
- Molhabilidade padronizada: Fluxo de condensado direcionado
Exemplo prático de implementação
Para um cilindro pneumático sem haste que funciona num ambiente de alta temperatura:
| Método de melhoramento | Implementação | h Melhoria | Redução da temperatura |
|---|---|---|---|
| Pin Fins (6mm) | Aletas de encaixe em alumínio, espaçamento de 10 mm | 180% | 12°C |
| Fluxo de ar direcionado | Ventoinha DC de 80mm, 2W a 1,5 m/s | 320% | 18°C |
| Tratamento de superfície | Anodização preta | 40% | 3°C |
| Abordagem combinada | Todos os métodos integrados | 450% | 24°C |
Correlação do número de Nusselt para cálculos de projeto
Para cálculos de engenharia, o Número de Nusselt4 (Nu) fornece uma abordagem sem dimensões para a convecção:
Nu = hL/k
Onde:
- L = Comprimento caraterístico
- k = Condutividade térmica do fluido
Para a convecção forçada sobre uma placa plana:
Nu = 0,664Re^(1/2)Pr^(1/3) (fluxo laminar)
Nu = 0,037Re^(4/5)Pr^(1/3) (fluxo turbulento)
Onde:
- Re = Número de Reynolds (velocidade × comprimento × densidade / viscosidade)
- Pr = Número de Prandtl (calor específico × viscosidade / condutividade térmica)
Estas correlações permitem aos engenheiros prever os coeficientes de convecção para diferentes configurações e otimizar as estratégias de arrefecimento em conformidade.
Modelo de eficiência de radiação: Quando é que a radiação térmica é importante nos sistemas pneumáticos?
A radiação é frequentemente negligenciada na gestão térmica de sistemas pneumáticos, mas pode ser responsável por 15-30% da transferência total de calor em muitas aplicações. Compreender quando e como otimizar a transferência de calor radiativo é crucial para uma gestão térmica abrangente.
A transferência de calor por radiação segue a Lei de Stefan-Boltzmann5: Q = εσA(T₁⁴-T₂⁴), em que ε é a emissividade da superfície, σ é a constante de Stefan-Boltzmann, A é a área da superfície e T₁ e T₂ são as temperaturas absolutas da superfície emissora e do ambiente. A eficiência da radiação em sistemas pneumáticos depende principalmente da emissividade da superfície, do diferencial de temperatura e dos factores de visão entre os componentes e o seu ambiente.
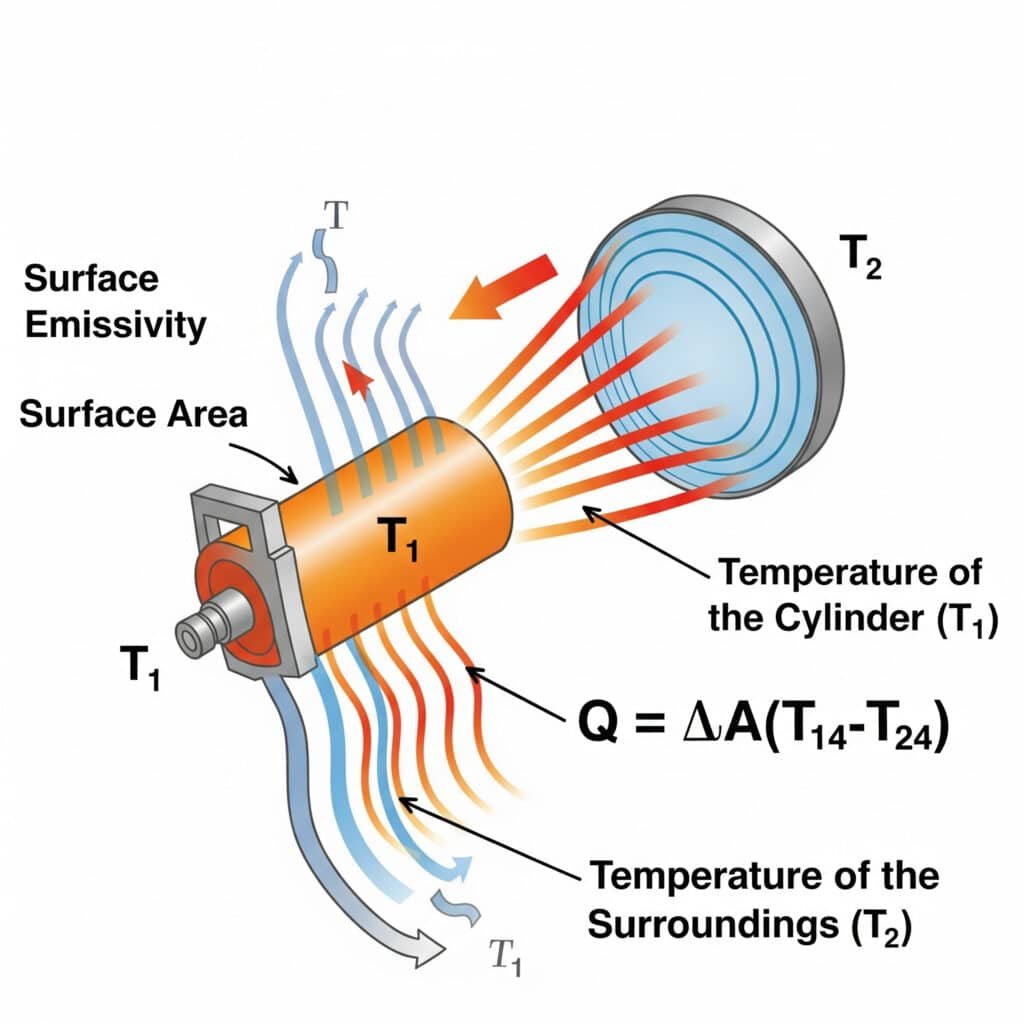
Ajudei recentemente um fabricante de equipamento de semicondutores no Oregon a resolver problemas de sobreaquecimento com os seus cilindros de precisão sem haste. Os seus engenheiros tinham-se concentrado exclusivamente na condução e na convecção, mas não se tinham apercebido da radiação. Ao aplicar um revestimento de elevada emissividade (aumentando ε de 0,11 para 0,92), melhorámos a transferência de calor por radiação em mais de 700%. Esta solução simples e passiva reduziu as temperaturas de funcionamento em 9°C sem quaisquer peças móveis ou consumo de energia - um requisito crítico no ambiente de sala limpa.
Fundamentos da transferência de calor por radiação
A equação básica que rege a transferência radiativa de calor é:
Q = εσA(T₁⁴-T₂⁴)
Onde:
- Q = Taxa de transferência de calor (W)
- ε = Emissividade (sem dimensão, 0-1)
- σ = constante de Stefan-Boltzmann (5,67 × 10-⁸ W/m²-K⁴)
- A = Área de superfície (m²)
- T₁ = Temperatura absoluta da superfície (K)
- T₂ = Temperatura absoluta do meio envolvente (K)
Valores de Emissividade de Superfície para Materiais Pneumáticos Comuns
| Material/Superfície | Emissividade (ε) | Eficiência de radiação | Potencial de melhoramento |
|---|---|---|---|
| Alumínio polido | 0.04-0.06 | Muito pobre | >1500% melhoria possível |
| Alumínio anodizado | 0.7-0.9 | Excelente | Já optimizado |
| Aço inoxidável (polido) | 0.07-0.14 | Pobres | >600% melhoria possível |
| Aço inoxidável (oxidado) | 0.6-0.85 | Bom | Possível melhoria moderada |
| Aço (polido) | 0.07-0.10 | Pobres | >900% melhoria possível |
| Aço (oxidado) | 0.7-0.9 | Excelente | Já optimizado |
| Superfícies pintadas | 0.8-0.98 | Excelente | Já optimizado |
| PTFE (branco) | 0.8-0.9 | Excelente | Já optimizado |
| Borracha nitrílica | 0.86-0.94 | Excelente | Já optimizado |
Ver considerações sobre os factores
A troca de radiação depende não só da emissividade, mas também das relações geométricas entre as superfícies:
F₁₂ = Fração da radiação que sai da superfície 1 e atinge a superfície 2
Para geometrias complexas, os factores de visualização podem ser calculados utilizando:
- Soluções analíticas para geometrias simples
- Ver álgebra de factores para combinar soluções conhecidas
- Métodos numéricos para arranjos complexos
- Aproximações empíricas para uma engenharia prática
Dependência da radiação em relação à temperatura
A relação entre a quarta potência e a temperatura torna a radiação particularmente eficaz a temperaturas mais elevadas:
| Temperatura da superfície | Percentagem de transferência de calor por radiação* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Assumindo condições de convecção natural, ε = 0,8, 25°C ambiente
Estratégias de melhoria da eficiência da radiação
Com base na minha experiência com sistemas pneumáticos industriais, eis as abordagens mais eficazes para melhorar a transferência de calor por radiação:
Modificação da Emissividade da Superfície
Revestimentos de alta emissividade
- Anodização preta para alumínio (ε ≈ 0,8-0,9)
- Óxido negro para aço (ε ≈ 0,7-0,8)
- Revestimentos cerâmicos especiais (ε ≈ 0,9-0,98)Texturização de superfícies
- A micro-rugosidade aumenta a emissividade efectiva
- As superfícies porosas melhoram as propriedades radiativas
- Melhorias combinadas de emissividade/convecção
Otimização ambiental
Gestão da temperatura ambiente
- Proteção contra equipamentos/processos quentes
- Paredes/tectos frios para uma melhor troca de radiação
- Barreiras reflectoras para direcionar a radiação para superfícies mais friasVer Fator de Melhoria
- Orientação para maximizar a exposição a superfícies frias
- Remoção de objectos de bloqueio
- Reflectores para melhorar a troca de radiação com as zonas mais frias
Estudo de caso: Melhoria da radiação na pneumática de precisão
Para um cilindro sem haste de alta precisão num ambiente de sala limpa:
| Parâmetro | Desenho original | Conceção com radiação reforçada | Melhoria |
|---|---|---|---|
| Material da superfície | Alumínio polido (ε ≈ 0,06) | Alumínio revestido a cerâmica (ε ≈ 0,94) | 1467% aumento da emissividade |
| Transferência de calor por radiação | 2.1W | 32.7W | 1457% aumento da radiação |
| Temperatura de funcionamento | 68°C | 59°C | Redução de 9°C |
| Vida útil do componente | 8 meses | >24 meses | Melhoria de 3× |
| Custo de implementação | – | $175 por cilindro | 4,2 meses de retorno |
Radiação vs. Outros Modos de Transferência de Calor
Compreender quando é que a radiação domina é crucial para uma gestão térmica eficiente:
| Estado | Dominância de condução | Dominância da convecção | Domínio da radiação |
|---|---|---|---|
| Gama de temperaturas | Baixo a alto | Baixo a médio | Médio a elevado |
| Propriedades do material | Materiais de alto k | Baixo k, elevada área de superfície | Superfícies ε elevadas |
| Factores ambientais | Bom contacto térmico | Ar em movimento, ventoinhas | Grande diferencial de temperatura |
| Restrições de espaço | Embalagem apertada | Fluxo de ar aberto | Vista para os arredores mais frescos |
| Melhores aplicações | Interfaces de componentes | Arrefecimento geral | Superfícies quentes, vácuo, ar parado |
Conclusão
O domínio dos princípios de transferência de calor - cálculo do coeficiente de condução, métodos de melhoria da convecção e modelação da eficiência da radiação - fornece a base para uma gestão térmica eficaz em sistemas pneumáticos. Ao aplicar estes princípios, é possível reduzir as temperaturas de funcionamento, prolongar a vida útil dos componentes e melhorar a eficiência energética, assegurando simultaneamente um funcionamento fiável, mesmo em ambientes difíceis.
Perguntas frequentes sobre a transferência de calor em sistemas pneumáticos
Qual é o aumento típico de temperatura nos cilindros pneumáticos durante o funcionamento?
Os cilindros pneumáticos sofrem normalmente aumentos de temperatura de 20-40°C acima da temperatura ambiente durante o funcionamento contínuo. Este aumento resulta da fricção entre os vedantes e as paredes do cilindro, do aquecimento do ar por compressão e da conversão do trabalho mecânico em calor. Os cilindros sem haste registam frequentemente aumentos de temperatura mais elevados (30-50°C) devido aos seus sistemas de vedação mais complexos e à geração de calor concentrada no conjunto rolamento/vedante.
Como é que a pressão de funcionamento afecta a produção de calor em sistemas pneumáticos?
A pressão de funcionamento tem um impacto significativo na produção de calor, sendo que as pressões mais elevadas criam mais calor através de vários mecanismos. Cada aumento de 1 bar na pressão de funcionamento aumenta tipicamente a produção de calor em 8-12% devido a maiores forças de fricção entre vedantes e superfícies, maior aquecimento por compressão e maiores perdas relacionadas com fugas. Esta relação é aproximadamente linear em gamas de funcionamento normais (3-10 bar).
Qual é a melhor abordagem de arrefecimento para componentes pneumáticos em diferentes ambientes?
A abordagem de arrefecimento ideal varia consoante o ambiente: em ambientes limpos e de temperatura moderada (15-30°C), a convecção natural com um espaçamento adequado entre os componentes é frequentemente suficiente. Em ambientes com temperaturas elevadas (30-50°C), torna-se necessária a convecção forçada utilizando ventoinhas ou ar comprimido. Em condições extremamente quentes (>50°C) ou quando o fluxo de ar é restrito, podem ser necessários métodos de arrefecimento ativo como arrefecedores termoeléctricos ou arrefecimento líquido. Em todos os casos, a maximização da radiação através de superfícies de elevada emissividade proporciona um arrefecimento passivo adicional.
Como é que se calcula a transferência total de calor de um componente pneumático?
Calcule a transferência total de calor somando as contribuições de cada mecanismo: Qtotal = Qcondução + Qconvecção + Qradiação. Para condução, use Q = kA(T₁-T₂)/L para cada caminho de calor. Para a convecção, use Q = hA(Ts-T∞) com coeficientes de convecção apropriados. Para a radiação, utilizar Q = εσA(T₁⁴-T₂⁴). Na maioria das aplicações pneumáticas industriais que operam a 30-80°C, a distribuição aproximada é de 20-40% de condução, 40-70% de convecção e 10-30% de radiação.
Qual é a relação entre a temperatura e a vida útil dos componentes pneumáticos?
A vida útil dos componentes diminui exponencialmente com o aumento da temperatura, seguindo uma relação de Arrhenius modificada. Como regra geral, cada aumento de 10°C na temperatura de funcionamento reduz a vida útil do vedante e do componente em 40-50%. Isto significa que um componente a funcionar a 70°C pode durar apenas um terço do tempo que o mesmo componente a 50°C. Esta relação é particularmente crítica para componentes de polímeros como vedantes, rolamentos e juntas, que determinam frequentemente o intervalo de manutenção dos sistemas pneumáticos.
-
Fornece uma explicação básica da Lei de Fourier, o princípio fundamental que descreve como o calor é conduzido através de materiais sólidos com base na sua condutividade térmica e gradiente de temperatura. ↩
-
Explica a função e os tipos de Materiais de Interface Térmica (TIMs), que são utilizados para preencher espaços de ar microscópicos entre componentes para melhorar a condução de calor e reduzir a resistência térmica. ↩
-
Detalha os princípios da Lei de Newton do arrefecimento, que rege a forma como os objectos arrefecem através da transferência de calor para o fluido circundante por convecção, um fator chave na conceção do sistema de arrefecimento. ↩
-
Oferece uma análise aprofundada do número de Nusselt, uma quantidade crítica sem dimensão na dinâmica dos fluidos e na transferência de calor que representa a relação entre a transferência de calor por convecção e por condução através de uma fronteira. ↩
-
Descreve a Lei de Stefan-Boltzmann, o princípio físico fundamental que quantifica a energia total irradiada por um corpo negro, que é essencial para calcular a perda de calor de superfícies quentes. ↩


