
Já alguma vez entrou no chão da sua fábrica e foi atingido pelo inconfundível silvo dos sistemas pneumáticos? Esse ruído não é apenas um incómodo - representa energia desperdiçada, potenciais problemas regulamentares e um sinal de aviso de funcionamento ineficiente.
O ruído acústico em sistemas pneumáticos é gerado através de três mecanismos principais: expansão de gás durante libertações de pressão, vibração mecânica de componentes e fluxo turbulento em tubos e acessórios. A compreensão destes mecanismos permite aos engenheiros implementar estratégias de redução de ruído direcionadas que melhoram a segurança no local de trabalho, aumentam a eficiência energética e prolongam a vida útil do equipamento.
No mês passado, visitei uma fábrica de produtos farmacêuticos em Nova Jérsia, onde o ruído excessivo dos seus cilindros sem haste estava a causar preocupações regulamentares. A sua equipa tinha tentado soluções genéricas sem sucesso. Ao analisar os mecanismos específicos de geração de ruído, reduzimos o ruído do sistema em 14 dBA - passando de um risco regulamentar para uma situação de conformidade. Deixe-me mostrar-lhe como o fizemos.
Índice
- Nível sonoro de expansão de gás: Que fórmula prevê o ruído dos gases de escape pneumáticos?
- Espectro de vibrações mecânicas: como é que a análise de frequências pode identificar as fontes de ruído?
- Perda de inserção do silenciador: Que cálculos orientam o design eficaz do silenciador?
- Conclusão
- Perguntas frequentes sobre o ruído do sistema pneumático
Nível sonoro de expansão de gás: Que fórmula prevê o ruído dos gases de escape pneumáticos?
A expansão súbita do ar comprimido durante o funcionamento da válvula ou a exaustão do cilindro cria uma das fontes de ruído mais significativas nos sistemas pneumáticos. Compreender a relação matemática entre os parâmetros do sistema e a emissão de ruído é essencial para uma atenuação eficaz.
O nível de potência sonora da expansão do gás pode ser calculado utilizando a fórmula: Lw = 10 log₁₀(W/W₀), onde W é a potência acústica em watts e W₀ é a potência de referência (10-¹² watts). Para sistemas pneumáticos, W pode ser estimado como W = η × m × (c²/2), em que η é a eficiência acústica, m é o caudal mássico e c é a velocidade do gás.
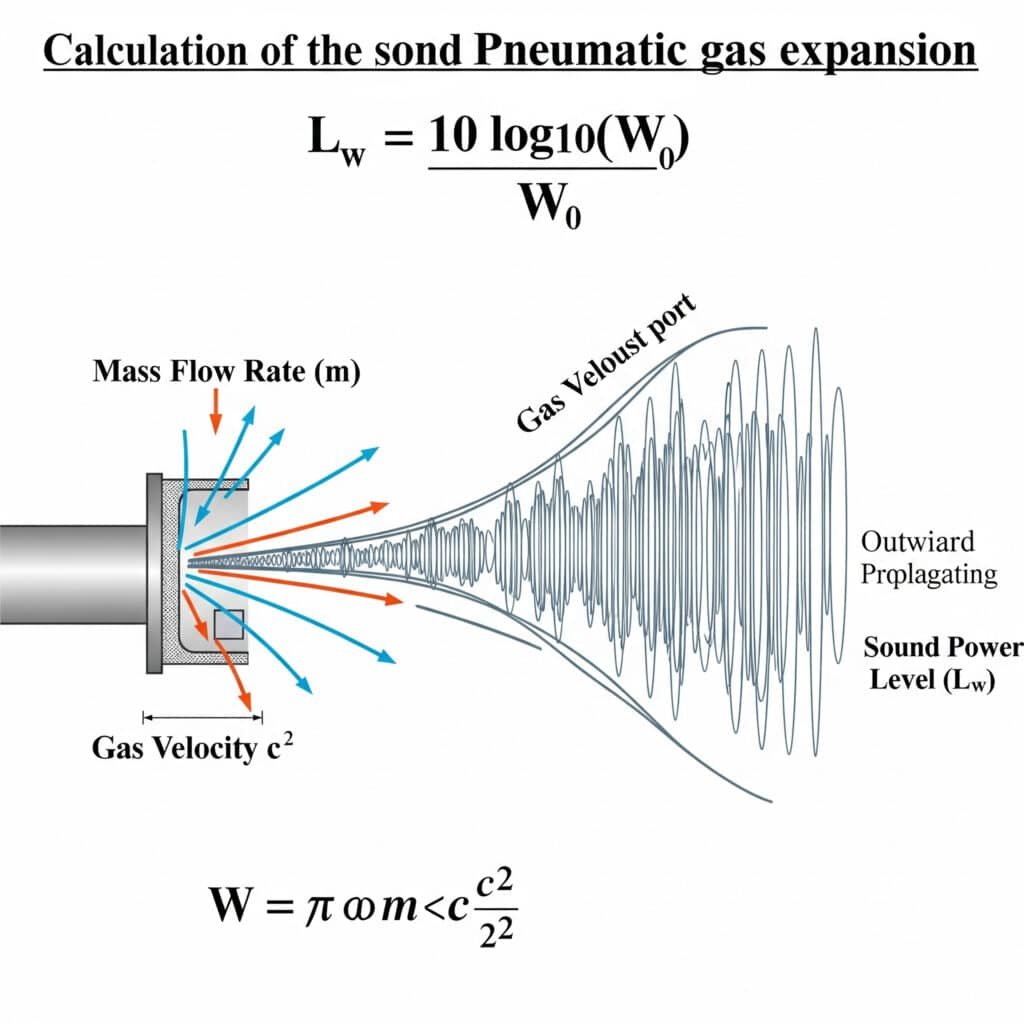
Lembro-me de ter resolvido problemas numa linha de embalagem em Illinois, onde os níveis de ruído excediam os 95 dBA - muito acima dos Limites OSHA1. A equipa de manutenção tinha-se concentrado nas fontes mecânicas, mas a nossa análise revelou que 70% do ruído provinha das portas de escape. Aplicando a fórmula de expansão de gás, identificámos que a pressão de funcionamento era 2,2 bar superior à necessária, criando um ruído de escape excessivo. Este simples ajuste de pressão reduziu o ruído em 8 dBA sem afetar o desempenho.
Equações fundamentais do ruído de expansão do gás
Vamos analisar as principais fórmulas para prever o ruído de expansão:
Cálculo da potência sonora
A potência acústica gerada pela expansão do gás pode ser calculada como:
W = η × m × (c²/2)
Onde:
- W = Potência acústica (watts)
- η = Eficiência acústica (normalmente 0,001-0,01 para exaustores pneumáticos)
- m = Caudal mássico (kg/s)
- c = Velocidade do gás nos gases de escape (m/s)
O nível de potência sonora em decibéis é então:
Lw = 10 log₁₀(W/W₀)
Em que W₀ é a potência de referência de 10-¹² watts.
Determinação do caudal mássico
O caudal mássico através de um orifício pode ser calculado como
m = Cd × A × p₁ × √(2γ/(γ-1) × (RT₁) × [(p₂/p₁)^(2/γ) - (p₂/p₁)^((γ+1)/γ)])
Onde:
- Cd = Coeficiente de descarga (normalmente 0,6-0,8)
- A = Área do orifício (m²)
- p₁ = Pressão absoluta a montante (Pa)
- p₂ = Pressão absoluta a jusante (Pa)
- γ = Rácio de calor específico (1,4 para o ar)
- R = Constante dos gases para o ar (287 J/kg-K)
- T₁ = Temperatura a montante (K)
Para um caudal estrangulado (comum em exaustores pneumáticos), isto simplifica-se para:
m = Cd × A × p₁ × √(γ/(RT₁)) × (2/(γ+1))^((γ+1)/(2(γ-1)))
Factores que afectam o ruído de expansão do gás
| Fator | Impacto no nível de ruído | Abordagem de atenuação |
|---|---|---|
| Pressão de funcionamento | Aumento de 3-4 dBA por barra | Reduzir a pressão do sistema para o mínimo necessário |
| Tamanho da porta de escape | Portas mais pequenas aumentam a velocidade e o ruído | Utilizar portas de tamanho adequado para os requisitos de caudal |
| Temperatura dos gases de escape | Temperaturas mais elevadas aumentam o ruído | Permitir o arrefecimento antes da expansão, sempre que possível |
| Rácio de expansão | Rácios mais elevados criam mais ruído | Expansão da fase através de várias etapas |
| Caudal | A duplicação do caudal aumenta o ruído em ~3 dBA | Utilizar vários tubos de escape mais pequenos em vez de um grande |
Exemplo prático de previsão de ruído
Para um cilindro sem haste típico com:
- Pressão de funcionamento: 6 bar (600.000 Pa)
- Diâmetro da porta de escape: 4 mm (área = 1,26 × 10-⁵ m²)
- Coeficiente de descarga: 0,7
- Eficiência acústica: 0,005
O caudal mássico durante o escape seria aproximadamente:
m = 0,7 × 1,26 × 10-⁵ × 600.000 × 0,0404 = 0,0214 kg/s
Admitindo uma velocidade de escape de 343 m/s (velocidade sónica), a potência acústica seria
W = 0,005 × 0,0214 × (343²/2) = 6,29 watts
O nível de potência sonora resultante:
Lw = 10 log₁₀(6,29/10-¹²) = 128 dB
Este elevado nível de potência sonora explica porque é que os escapes pneumáticos não silenciados são fontes de ruído tão significativas em ambientes industriais.
Espectro de vibrações mecânicas: como é que a análise de frequências pode identificar as fontes de ruído?
As vibrações mecânicas em componentes pneumáticos geram assinaturas de ruído distintas que podem ser analisadas para identificar problemas específicos. A análise do espetro de frequência fornece a chave para identificar e tratar estas fontes de ruído mecânico.
A vibração mecânica em sistemas pneumáticos produz ruído com espectros de frequência caraterísticos que podem ser analisados utilizando Transformada rápida de Fourier (FFT)2 técnicas. As principais gamas de frequências incluem vibrações estruturais de baixa frequência (10-100 Hz), harmónicas operacionais de média frequência (100-1000 Hz) e vibrações induzidas pelo fluxo de alta frequência (1-10 kHz), cada uma exigindo diferentes abordagens de mitigação.
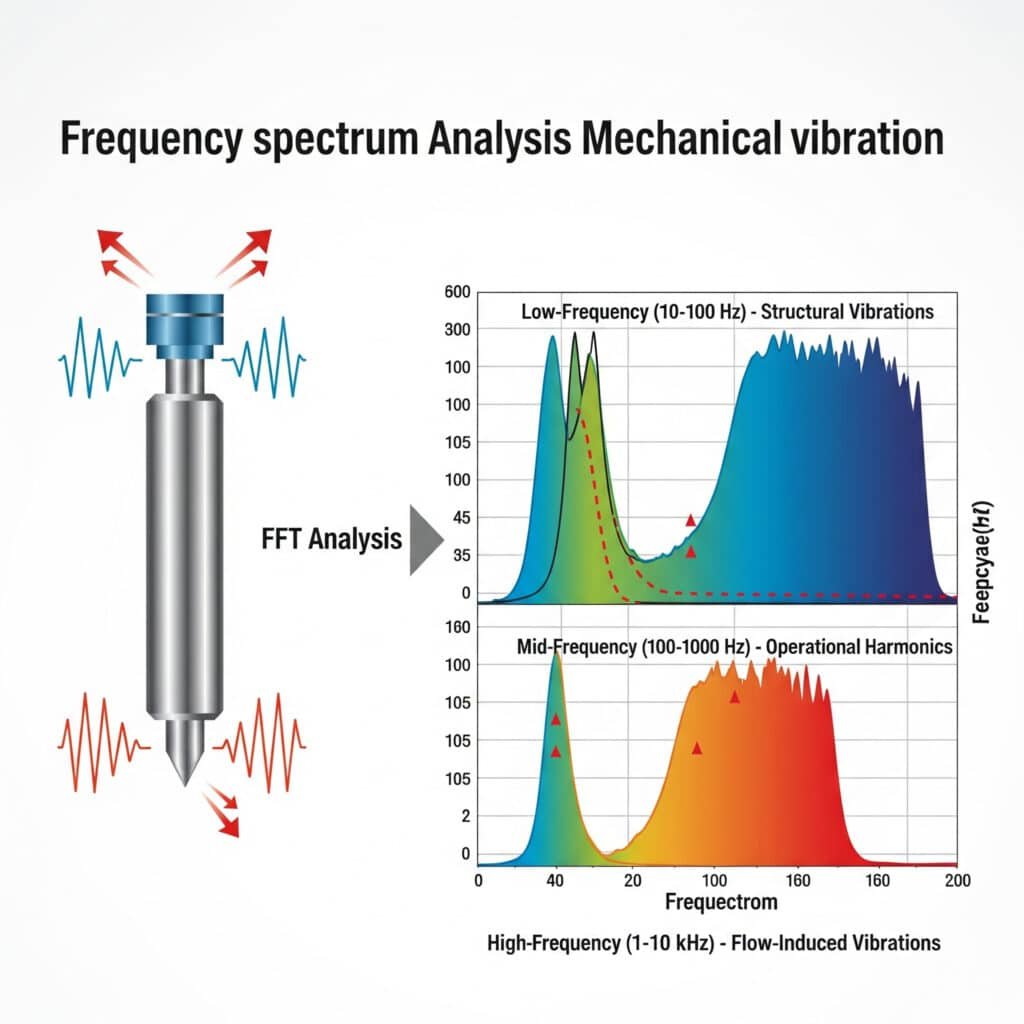
Durante uma consulta num fabricante de peças para automóveis no Michigan, a sua equipa de manutenção estava a debater-se com o ruído excessivo de um sistema de transferência de cilindros sem haste. A resolução convencional de problemas não tinha conseguido identificar a fonte. A nossa análise do espetro de vibração revelou um pico distinto a 237 Hz - correspondendo exatamente à ressonância da banda de vedação interna do cilindro. Ao modificar o sistema de montagem para amortecer esta frequência específica, reduzimos o ruído em 11 dBA sem qualquer interrupção da produção.
Metodologia de análise do espetro de frequência
A análise eficaz das vibrações segue uma abordagem sistemática:
- Configuração da medição: Utilização de acelerómetros e microfones acústicos
- Aquisição de dados: Captação de sinais de vibração no domínio do tempo
- Análise FFT: Conversão para o domínio da frequência
- Mapeamento espetral: Identificação de frequências caraterísticas
- Atribuição de fontes: Correspondência de frequências a componentes específicos
Gamas de frequências caraterísticas em sistemas pneumáticos
| Gama de frequências | Fontes típicas | Caraterísticas acústicas |
|---|---|---|
| 10-50 Hz | Ressonância estrutural, problemas de montagem | Ruído de baixa frequência, mais sentido do que ouvido |
| 50-200 Hz | Impactos do pistão, acionamento da válvula | Batida ou pancada distinta |
| 200-500 Hz | Atrito da vedação, ressonância interna | Zumbido ou zumbido de média frequência |
| 500-2000 Hz | Turbulência do fluxo, pulsações de pressão | Sibilância com componentes tonais |
| 2-10 kHz | Fugas, fluxo de alta velocidade | Sibilo agudo, mais irritante para o ouvido humano |
| >10 kHz | Micro-turbulência, expansão de gás | Componentes ultra-sónicos, indicador de perda de energia |
Vias de transmissão de vibrações
O ruído das vibrações mecânicas segue vários caminhos:
Transmissão através de estruturas
As vibrações deslocam-se através de componentes sólidos:
- O componente vibra devido a forças internas
- Transferência de vibrações através dos pontos de montagem
- As estruturas ligadas amplificam e irradiam o som
- As grandes superfícies funcionam como radiadores de som eficientes
Transmissão por via aérea
Radiação direta do som a partir de superfícies vibrantes:
- A vibração da superfície desloca o ar
- O deslocamento cria ondas de pressão
- As ondas propagam-se no ar
- O tamanho da superfície radiante determina a eficiência
Estudo de caso: Análise de Vibração de Cilindro sem Haste
Para um cilindro magnético sem haste que apresente um ruído excessivo:
| Frequência (Hz) | Amplitude (dB) | Identificação da fonte | Estratégia de atenuação |
|---|---|---|---|
| 43 | 78 | Ressonância de montagem | Suporte de montagem reforçado |
| 86 | 65 | Harmónica da ressonância de montagem | Abordado com ressonância primária |
| 237 | 91 | Ressonância da banda de selagem | Material de amortecimento adicionado ao corpo do cilindro |
| 474 | 83 | Harmónica da banda de vedação | Abordado com ressonância primária |
| 1250 | 72 | Turbulência do fluxo de ar | Conceção modificada do porto |
| 3700 | 68 | Fugas nas tampas das extremidades | Vedantes substituídos |
As estratégias de atenuação combinadas reduziram o ruído global em 14 dBA, sendo a melhoria mais significativa resultante da resolução da ressonância de 237 Hz.
Técnicas avançadas de análise de vibrações
Para além da análise FFT básica, várias técnicas avançadas permitem obter informações mais aprofundadas:
Análise de pedidos
Particularmente útil para sistemas de velocidade variável:
- Frequências de rastreio que aumentam com a velocidade operacional
- Separa os componentes dependentes da velocidade dos componentes de frequência fixa
- Identifica problemas relacionados com fases específicas do movimento
Análise da forma de deflexão operacional (ODS)
Mapeia os padrões de vibração em todo o sistema:
- Vários pontos de medição criam um "mapa" de vibrações
- Revela como as estruturas se movem durante o funcionamento
- Identifica os locais ideais para tratamentos de amortecimento
Análise Modal
Determina as frequências naturais e as formas próprias:
- Identifica as frequências de ressonância antes do funcionamento
- Prevê potenciais frequências de problemas
- Orienta as modificações estruturais para evitar a ressonância
Perda de inserção do silenciador: Que cálculos orientam o design eficaz do silenciador?
Silenciadores e silenciadores são essenciais para reduzir o ruído do sistema pneumático, mas a sua conceção deve basear-se em cálculos de engenharia de som para garantir a eficácia sem comprometer o desempenho do sistema.
Silenciador perda de inserção3 (IL) quantifica a eficácia da redução do ruído e pode ser calculada como IL = Lw₁ - Lw₂, em que Lw₁ é o nível de potência sonora sem o silenciador e Lw₂ é o nível com o silenciador instalado. Para sistemas pneumáticos, os silenciadores eficazes atingem normalmente uma perda de inserção de 15-30 dB na gama de frequências críticas de 500 Hz a 4 kHz, mantendo uma contrapressão aceitável.
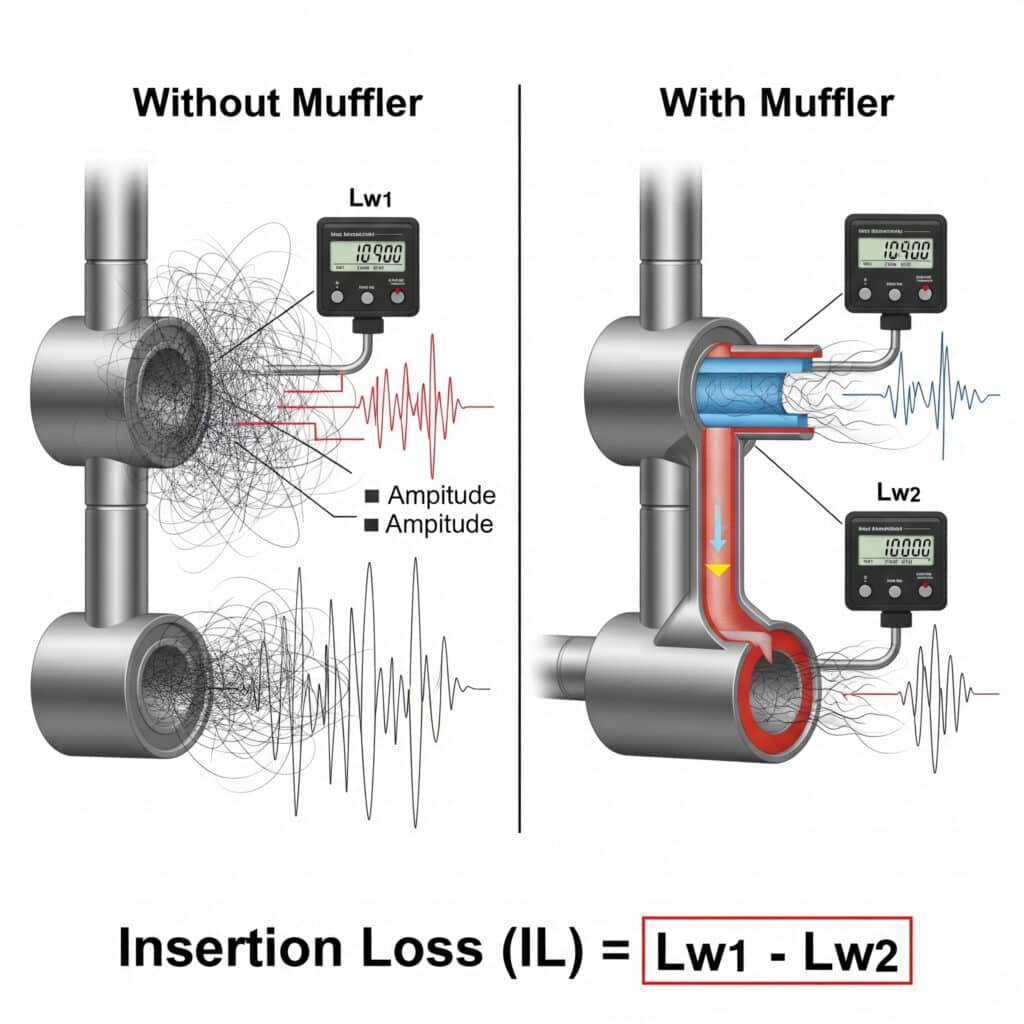
Recentemente, ajudei um fabricante de dispositivos médicos em Massachusetts a resolver um problema de ruído difícil com o seu sistema de cilindros de precisão sem haste. A sua tentativa inicial de utilizar silenciadores prontos a usar reduziu o ruído mas criou uma contrapressão excessiva que afectou os tempos de ciclo. Ao calcular a perda de inserção necessária em bandas de frequência específicas e ao conceber um silenciador multi-câmara personalizado, conseguimos uma redução de ruído de 24 dB com um impacto mínimo no desempenho. O resultado foi um sistema que satisfazia os seus requisitos de ruído e precisão.
Fundamentos da perda de inserção do silenciador
A equação central para a perda de inserção é:
IL = Lw₁ - Lw₂
Onde:
- IL = Perda de inserção (dB)
- Lw₁ = Nível de potência sonora sem silenciador (dB)
- Lw₂ = Nível de potência sonora com silenciador (dB)
Para uma análise específica da frequência, isto torna-se:
IL(f) = Lw₁(f) - Lw₂(f)
Onde f indica a banda de frequência específica que está a ser analisada.
Parâmetros de projeto do silenciador e seus efeitos
| Parâmetro | Efeito na perda de inserção | Efeito na contrapressão | Gama óptima |
|---|---|---|---|
| Volume da câmara | Um volume maior aumenta a IL de baixa frequência | Impacto mínimo se for corretamente concebido | 10-30× volume do orifício de escape |
| Número de câmaras | Mais câmaras aumentam a IL de média frequência | Aumenta com mais câmaras | 2-4 câmaras para a maioria das aplicações |
| Rácio de expansão | Rácios mais elevados melhoram a IL | Impacto mínimo se for gradual | Rácio de área de 4:1 a 16:1 |
| Material acústico | Melhora a IL de alta frequência | Impacto mínimo com uma conceção adequada | 10-50 mm de espessura |
| Perfuração do deflector | Afecta a IL de média frequência | Impacto significativo | 30-50% área aberta |
| Comprimento do percurso do fluxo | Caminhos mais longos melhoram a IL de baixa frequência | Aumenta com o comprimento | 3-10× diâmetro do porto |
Modelos teóricos para a previsão da perda de inserção
Vários modelos podem prever a perda de inserção para diferentes tipos de silenciadores:
Modelo de câmara de expansão
Para câmaras de expansão simples:
IL = 10 log₁₀[1 + 0,25(m-1/m)² sin²(kL)]
Onde:
- m = rácio de área (área da câmara / área do tubo)
- k = Número de onda (2πf/c, em que f é a frequência e c é a velocidade do som)
- L = Comprimento da câmara
Modelo de silenciador dissipativo
Para silenciadores com materiais de absorção de som:
IL = 8,68α(L/d)
Onde:
- α = Coeficiente de absorção do material
- L = Comprimento do troço revestido
- d = Diâmetro da via de escoamento
Modelo de silenciador reativo (Ressonador Helmholtz4)
Para silenciadores do tipo ressonador:
IL = 10 log₁₀[1 + (ρc/2S)² × (V/L'c²) × ω²/((ω₀² - ω²)² + (Rω/ρc)²)]
Onde:
- ρ = Densidade do ar
- c = Velocidade do som
- S = Área da secção transversal do pescoço
- V = Volume da cavidade
- L' = Comprimento efetivo do pescoço
- ω = Frequência angular
- ω₀ = Frequência de ressonância
- R = Resistência acústica
Processo prático de seleção de silenciadores
Selecionar ou conceber um silenciador adequado:
- Medir o espetro de ruído: Determinar o conteúdo de frequência do ruído
- Calcular o IL necessário: Determinar a redução necessária por frequência
- Avaliar os requisitos de fluxo: Calcular a contrapressão máxima admissível
- Selecionar o tipo de silenciador:
- Reativo (câmaras de expansão) para baixas frequências
- Dissipativo (absorvente) para altas frequências
- Combinação para ruído de banda larga - Verificar o desempenho: Teste de perda de inserção e contrapressão
Considerações sobre a contrapressão
Uma contrapressão excessiva pode afetar significativamente o desempenho do sistema:
Cálculo da contrapressão
A contrapressão pode ser estimada como:
ΔP = ρ(Q/Cd×A)²/2
Onde:
- ΔP = Queda de pressão (Pa)
- ρ = Densidade do ar (kg/m³)
- Q = Caudal (m³/s)
- Cd = Coeficiente de descarga
- A = Área de fluxo efetivo (m²)
Avaliação do impacto no desempenho
Para um cilindro sem haste com:
- Diâmetro do furo: 40 mm
- Curso: 500mm
- Duração do ciclo: 2 segundos
- Pressão de funcionamento: 6 bar
Cada 0,1 bar de contrapressão:
- Reduzir a força de saída em cerca de 1,7%
- Aumentar o tempo de ciclo em cerca de 2,3%
- Aumento do consumo de energia em cerca de 1,5%
Estudo de caso: Design de silenciadores personalizados
Para uma aplicação de cilindro sem haste de precisão com requisitos rigorosos de ruído:
| Parâmetro | Condição inicial | Silenciador de prateleira | Design personalizado |
|---|---|---|---|
| Nível sonoro | 89 dBA | 76 dBA | 65 dBA |
| Contrapressão | 0,05 bar | 0,42 bar | 0,11 bar |
| Tempo de ciclo | 1,8 segundos | 2,3 segundos | 1,9 segundos |
| Resposta de frequência | Banda larga | Fraco a 2-4 kHz | Optimizado em todo o espetro |
| Vida útil | N/A | 3 meses (entupimento) | >12 meses |
| Custo de implementação | N/A | $120 por ponto | $280 por ponto |
A conceção personalizada do silenciador proporcionou uma redução superior do ruído, mantendo um desempenho aceitável do sistema, com um período de retorno do investimento inferior a 6 meses, tendo em conta as melhorias de produtividade.
Conclusão
A compreensão dos mecanismos de geração de ruído acústico - níveis sonoros de expansão de gás, espectros de vibração mecânica e cálculos de perda de inserção do silenciador - fornece a base para um controlo eficaz do ruído em sistemas pneumáticos. Ao aplicar estes princípios, é possível criar sistemas pneumáticos mais silenciosos, mais eficientes e mais fiáveis, assegurando simultaneamente a conformidade regulamentar e melhorando as condições do local de trabalho.
Perguntas frequentes sobre o ruído do sistema pneumático
Quais são os limites da OSHA para a exposição ao ruído de sistemas pneumáticos?
A OSHA limita a exposição ao ruído no local de trabalho a 90 dBA para uma média ponderada no tempo de 8 horas, com uma taxa de troca de 5 dBA. No entanto, o limite de exposição recomendado pelo NIOSH é mais conservador, 85 dBA. Os sistemas pneumáticos excedem frequentemente estes limites, sendo que os gases de escape não silenciados geram muitas vezes 90-110 dBA a um metro de distância, exigindo controlos de engenharia para o seu cumprimento.
Como é que a pressão de funcionamento afecta o ruído do sistema pneumático?
A pressão de funcionamento tem um impacto significativo na produção de ruído, com cada aumento de 1 bar na pressão a acrescentar normalmente 3-4 dBA aos níveis de ruído de escape. Esta relação é logarítmica e não linear, uma vez que a potência sonora aumenta com o quadrado do rácio de pressão. A redução da pressão do sistema para o mínimo necessário para o funcionamento é frequentemente a estratégia de redução de ruído mais simples e mais económica.
Qual é a diferença entre silenciadores reactivos e dissipativos para sistemas pneumáticos?
Os silenciadores reactivos utilizam câmaras e passagens para refletir as ondas sonoras e criar interferências destrutivas, tornando-os eficazes para o ruído de baixa frequência (abaixo de 500 Hz) com uma queda de pressão mínima. Os silenciadores dissipativos utilizam materiais de absorção de som para converter a energia acústica em calor, tornando-os mais eficazes para o ruído de alta frequência (acima de 500 Hz), mas mais susceptíveis à contaminação. Muitos silenciadores pneumáticos industriais combinam ambos os princípios para uma redução de ruído de banda larga.
Como é que posso identificar a fonte de ruído dominante no meu sistema pneumático?
Utilize uma abordagem sistemática, começando com testes operacionais: faça funcionar o sistema a diferentes pressões, velocidades e cargas enquanto mede o ruído. Em seguida, efectue o isolamento de componentes, operando elementos individuais separadamente. Finalmente, efectue uma análise de frequência utilizando um sonómetro com capacidade de banda de oitava - as frequências baixas (50-250 Hz) indicam tipicamente problemas estruturais, as frequências médias (250-2000 Hz) sugerem ruído operacional e as frequências altas (2-10 kHz) apontam para problemas de fluxo ou fugas.
Qual é a relação entre o nível de ruído e a distância de um componente pneumático?
O ruído dos componentes pneumáticos segue a lei do quadrado inverso em condições de campo livre, diminuindo aproximadamente 6 dB cada vez que a distância duplica. No entanto, em ambientes industriais típicos com superfícies reflectoras, a redução real é frequentemente de apenas 3-4 dB por duplicação da distância devido à reverberação. Isto significa que duplicar a distância de uma fonte de ruído de 90 dB pode apenas reduzir o nível para 86-87 dB em vez dos 84 dB teóricos.
-
Fornece os regulamentos oficiais da Administração de Segurança e Saúde Ocupacional (OSHA) e os limites de exposição permitidos (PEL) para o ruído no local de trabalho, que é um fator chave para a atenuação acústica. ↩
-
Explica o algoritmo da Transformada Rápida de Fourier (FFT), uma ferramenta matemática fundamental utilizada para converter um sinal no domínio do tempo (como uma vibração ou uma onda sonora) nos seus componentes de frequência constituintes para análise. ↩
-
Descreve a análise modal, uma técnica de engenharia avançada utilizada para determinar as propriedades dinâmicas inerentes a um sistema, tais como as suas frequências naturais e formas modais, para prever e evitar a ressonância. ↩
-
Oferece uma explicação pormenorizada da perda de inserção (IL), a principal métrica utilizada para quantificar o desempenho de um silenciador, medindo a redução do nível sonoro que proporciona. ↩



