As medições de pressão confundem até os engenheiros experientes. Já resolvi inúmeros problemas de sistemas pneumáticos em que referências de pressão incorrectas causaram problemas de desempenho. Compreender a pressão absoluta evita erros de cálculo dispendiosos e falhas no sistema.
A pressão absoluta (pressão ABS) mede a pressão relativa a um vácuo perfeito, incluindo a pressão atmosférica na medição. É igual à pressão manométrica mais a pressão atmosférica (14,7 PSI ao nível do mar), fornecendo a verdadeira pressão total que actua sobre os componentes pneumáticos.
Na semana passada, ajudei o Thomas, um engenheiro de design de uma empresa de fabrico holandesa, a resolver problemas de desempenho relacionados com a altitude com o seu cilindro pneumático sem haste1 sistema. Os seus cálculos funcionaram perfeitamente ao nível do mar, mas falharam nas suas instalações na montanha. O problema não era a falha do equipamento - eram os conceitos errados sobre a pressão absoluta.
Índice
- O que é a pressão absoluta e como é que ela difere da pressão manométrica?
- Porque é que a pressão absoluta é crítica para os cálculos pneumáticos?
- Como é que a altitude afecta a pressão absoluta nos sistemas pneumáticos?
- Quais são as aplicações comuns da pressão absoluta em ambientes industriais?
- Como se faz a conversão entre diferentes medições de pressão?
- Que erros cometem os engenheiros nos cálculos da pressão absoluta?
O que é a pressão absoluta e como é que ela difere da pressão manométrica?
A pressão absoluta representa a pressão total que actua sobre um sistema, medida a partir de um ponto de referência de vácuo perfeito. Esta medição inclui os efeitos da pressão atmosférica que a pressão manométrica ignora.
A pressão absoluta é igual à pressão manométrica mais a pressão atmosférica. Ao nível do mar, a pressão atmosférica é de 14,7 PSI, pelo que 80 PSIG de pressão manométrica é igual a 94,7 PSIA de pressão absoluta. Esta distinção é crucial para cálculos precisos do sistema pneumático.

Compreensão dos pontos de referência da pressão
Diferentes medições de pressão utilizam diferentes pontos de referência:
| Tipo de pressão | Ponto de referência | Símbolo | Intervalo típico |
|---|---|---|---|
| Absoluto | Aspiração perfeita | PSIA | 0 a 1000+ PSIA |
| Calibre | Atmosférico | PSIG | -14,7 a 1000+ PSIG |
| Diferencial | Entre dois pontos | PSID | Variável |
| Vácuo | Abaixo da atmosfera | "Hg | 0 a 29,92 "Hg |
Fundamentos da pressão absoluta
A pressão absoluta fornece a imagem completa da pressão. Inclui tanto a pressão aplicada como a pressão atmosférica que rodeia o sistema.
A relação fundamental é:
PSIA = PSIG + Pressão atmosférica
Em condições normais ao nível do mar:
PSIA = PSIG + 14,7
Limitações da pressão do manómetro
As medições da pressão manométrica ignoram as variações da pressão atmosférica. Isto cria problemas quando a pressão atmosférica muda devido à altitude ou às condições climatéricas.
A pressão manométrica funciona bem para a maioria das aplicações industriais porque a pressão atmosférica permanece relativamente constante em locais fixos. No entanto, a pressão absoluta torna-se crítica para:
- Cálculos de compensação de altitude
- Conceção do sistema de vácuo
- Aplicações da lei dos gases
- Cálculo do caudal
- Compensação da temperatura
Diferenças práticas de medição
Trabalhei recentemente com a Anna, uma engenheira de processos de uma plataforma offshore norueguesa. Os seus cálculos pneumáticos funcionavam perfeitamente em terra, mas falharam quando o equipamento passou a ser utilizado em operações no mar.
O problema era a variação da pressão atmosférica. Os sistemas meteorológicos criavam alterações de 1-2 PSI na pressão atmosférica que afectavam as leituras da pressão manométrica. Ao mudar para medições de pressão absoluta, eliminámos as variações de desempenho relacionadas com o clima.
Compreensão visual
Pense na pressão absoluta como a medição desde o fundo de uma piscina (vácuo perfeito) até à superfície da água (pressão do sistema). A pressão manométrica mede apenas desde o nível normal da água (pressão atmosférica) até à superfície.
Esta analogia ajuda a compreender porque é que a pressão absoluta fornece informações mais completas para os cálculos de engenharia.
Porque é que a pressão absoluta é crítica para os cálculos pneumáticos?
A pressão absoluta constitui a base para cálculos exactos de sistemas pneumáticos. Muitas fórmulas de engenharia requerem valores de pressão absoluta para produzir resultados corretos.
A pressão absoluta é essencial para os cálculos pneumáticos porque as leis dos gases, as equações de fluxo e as relações termodinâmicas utilizam valores de pressão absoluta. A utilização da pressão manométrica nestas fórmulas produz resultados incorrectos que podem levar a falhas no sistema.
Aplicações da lei dos gases
O lei dos gases ideais2 requer pressão absoluta para cálculos exactos:
PV = nRT
Onde:
- P = Pressão absoluta
- V = Volume
- n = Número de moles
- R = Constante do gás
- T = Temperatura absoluta3
A utilização da pressão manométrica nos cálculos da lei dos gases produz erros proporcionais à pressão atmosférica. Ao nível do mar, isto cria um erro de 15% na maioria dos cálculos.
Cálculos de caudal
As fórmulas de caudal pneumático requerem rácios de pressão absoluta:
Caudal ∝ √(P₁² - P₂²)
Em que P₁ e P₂ são pressões absolutas a montante e a jusante de uma restrição.
A utilização de pressões manométricas nos cálculos de caudal pode produzir erros superiores a 20%, conduzindo a componentes do sistema subdimensionados ou sobredimensionados.
Cálculos da força do cilindro
Enquanto os cálculos básicos de força (F = P × A) funcionam com pressão manométrica, as aplicações avançadas requerem pressão absoluta:
Compensação de altitude
A força de saída muda com a altitude devido às variações da pressão atmosférica. Os cálculos da pressão absoluta têm em conta estas alterações.
Efeitos da temperatura
Os cálculos de expansão e contração de gás requerem valores absolutos de pressão e temperatura para serem exactos.
Desempenho do compressor
Os cálculos de dimensionamento e desempenho do compressor utilizam rácios de pressão absoluta:
Rácio de compressão = P₂(abs) ÷ P₁(abs)
Este rácio determina os requisitos de fase do compressor e o consumo de energia. A utilização de pressões manométricas produz pressões incorrectas taxas de compressão4.
Exemplo do mundo real
Ajudei o Marcus, um supervisor de manutenção de uma fábrica de precisão suíça, a resolver um problema de desempenho inconsistente do cilindro sem haste. As suas instalações operavam a 3.000 pés de altitude, onde a pressão atmosférica é de 13,2 PSI em vez dos 14,7 PSI do nível do mar.
As suas leituras de pressão manométrica indicavam 80 PSIG, mas a pressão absoluta era de apenas 93,2 PSIA em vez dos 94,7 PSIA esperados. Esta diferença de 1,5 PSI reduziu a força de saída do cilindro em 1,6%, causando problemas de exatidão de posicionamento em aplicações de precisão.
Ao recalibrar os seus cálculos para a pressão atmosférica local, restaurámos o desempenho adequado do sistema.
Aplicações de vácuo
Os sistemas de vácuo requerem medições de pressão absoluta porque a pressão manométrica torna-se negativa abaixo da pressão atmosférica:
| Nível de vácuo | Pressão manométrica | Pressão absoluta |
|---|---|---|
| Vácuo bruto | -10 PSIG | 4,7 PSIA |
| Médio vácuo | -13 PSIG | 1,7 PSIA |
| Alto vácuo | -14,5 PSIG | 0,2 PSIA |
| Aspiração perfeita | -14,7 PSIG | 0,0 PSIA |
Como é que a altitude afecta a pressão absoluta nos sistemas pneumáticos?
A altitude tem um impacto significativo na pressão atmosférica, afectando o desempenho do sistema pneumático. A compreensão destes efeitos evita problemas de desempenho em instalações elevadas.
A pressão atmosférica diminui aproximadamente 0,5 PSI por cada 1.000 pés de aumento de altitude. Esta redução afecta os cálculos da pressão absoluta e pode reduzir a força de saída do cilindro pneumático em 3-4% por cada 1.000 pés de altitude.
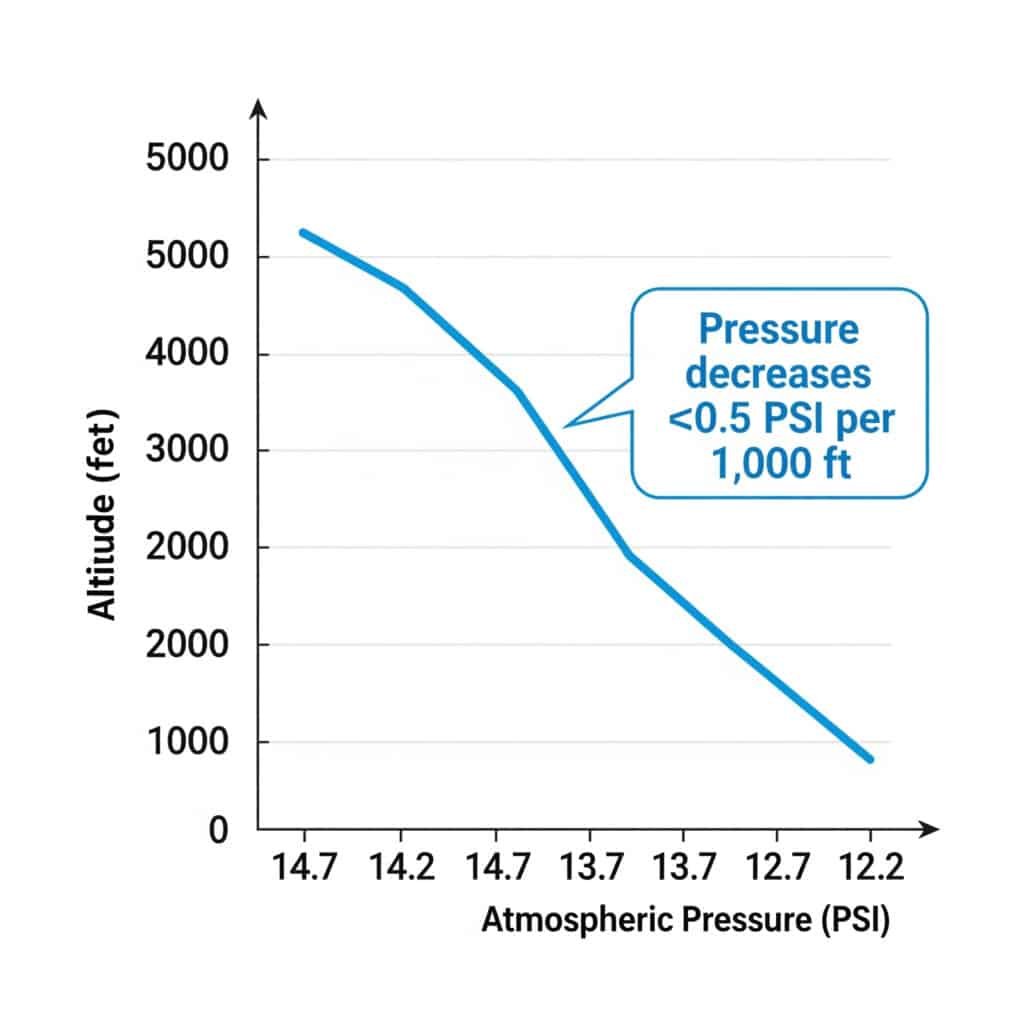
Pressão atmosférica vs. Altitude
A pressão atmosférica padrão varia de forma previsível com a altitude:
| Altitude (pés) | Pressão atmosférica (PSIA) | Redução da pressão |
|---|---|---|
| Nível do mar | 14.7 | 0% |
| 1,000 | 14.2 | 3.4% |
| 2,000 | 13.7 | 6.8% |
| 5,000 | 12.2 | 17.0% |
| 10,000 | 10.1 | 31.3% |
Força de saída Impacto
A redução da pressão atmosférica afecta os cálculos da força do cilindro quando se utiliza a pressão absoluta:
Pressão efectiva = pressão manométrica + pressão atmosférica local
Para um cilindro a funcionar a 80 PSIG:
- Nível do mar: 80 + 14,7 = 94,7 PSIA
- 5.000 pés: 80 + 12,2 = 92,2 PSIA
- Redução da força: 2.6%
Estratégias de compensação de altitude
Vários métodos compensam os efeitos da altitude:
Ajuste da pressão
Aumentar a pressão manométrica para manter a pressão absoluta constante:
Pressão manométrica requerida = Pressão absoluta alvo - Pressão atmosférica local
Redesenho do sistema
Redimensionar os cilindros para manter a força de saída em condições de pressão absoluta reduzida.
Compensação do sistema de controlo
Programar os sistemas de controlo para se adaptarem às variações locais da pressão atmosférica.
Efeitos combinados da temperatura e da altitude
Tanto a altitude como a temperatura afectam a densidade do ar e o desempenho do sistema:
Densidade do ar = (pressão absoluta × peso molecular) ÷ (constante do gás × temperatura absoluta)
As altitudes mais elevadas têm normalmente temperaturas mais baixas, compensando parcialmente os efeitos da redução da pressão na densidade do ar.
Aplicação em altitude no mundo real
Trabalhei com Carlos, um gestor de projectos que instalava sistemas pneumáticos numa exploração mineira no Peru, a 12.000 pés de altitude. Os seus cálculos ao nível do mar mostraram uma força adequada para aplicações de manuseamento de materiais.
Na altitude da instalação, a pressão atmosférica era de apenas 9,3 PSIA em comparação com os 14,7 PSIA do nível do mar. Esta redução de 37% na pressão atmosférica afectou significativamente o desempenho do sistema.
Nós compensámos por:
- Aumento da pressão de funcionamento de 80 para 95 PSIG
- Redimensionamento de cilindros críticos por 15%
- Adição de reforços de pressão para aplicações de força elevada
O sistema modificado apresentou o desempenho necessário apesar das condições extremas de altitude.
Efeitos meteorológicos em altitude
Os locais de elevada altitude registam maiores variações da pressão atmosférica devido às condições meteorológicas:
Variações do nível do mar
- Alta pressão: 15,2 PSIA (+0,5 PSI)
- Baixa pressão: 14,2 PSIA (-0,5 PSI)
- Alcance total: 1,0 PSI
Variações de alta altitude (10.000 pés)
- Alta pressão: 10,6 PSIA (+0,5 PSI)
- Baixa pressão: 9,6 PSIA (-0,5 PSI)
- Alcance total: 1,0 PSI (10% da pressão de base)
Quais são as aplicações comuns da pressão absoluta em ambientes industriais?
As medições de pressão absoluta são essenciais em numerosas aplicações industriais em que as relações de pressão exactas determinam o desempenho e a segurança do sistema.
As aplicações comuns de pressão absoluta incluem sistemas de vácuo, cálculos de caudal de gás, dimensionamento de compressores, compensação de altitude e processos termodinâmicos. Estas aplicações requerem pressão absoluta porque as medições da pressão manométrica fornecem informações incompletas.
Conceção do sistema de vácuo
As aplicações de vácuo requerem medições de pressão absoluta porque a pressão manométrica torna-se negativa abaixo das condições atmosféricas:
Dimensionamento da bomba de vácuo
A capacidade da bomba de vácuo depende dos rácios de pressão absoluta:
Velocidade de bombagem = Caudal volúmico ÷ (P₁ - P₂)
Em que P₁ e P₂ são as pressões absolutas à entrada e à saída da bomba.
Especificações do nível de vácuo
Os níveis de vácuo industriais utilizam medições de pressão absoluta:
| Aplicação | Nível de vácuo (PSIA) | Utilização típica |
|---|---|---|
| Manuseamento de materiais | 10-12 | Ventosas, transportadores |
| Embalagem | 5-8 | Embalagem a vácuo |
| Indústrias de processo | 1-3 | Destilação, secagem |
| Laboratório | 0.1-0.5 | Aplicações de investigação |
Medição de caudal de gás
Os cálculos exactos do caudal de gás requerem valores de pressão absoluta:
Condições de caudal estrangulado
O fluxo de gás fica estrangulado quando a pressão a jusante desce abaixo da pressão crítica:
Rácio de pressão crítica = 0,528 (para o ar)
Este cálculo requer pressões absolutas para determinar as limitações do caudal.
Cálculos de caudal mássico
O caudal mássico depende da pressão absoluta e da temperatura:
Caudal mássico = (pressão absoluta × área × velocidade) ÷ (constante do gás × temperatura absoluta)
Aplicações de compressores
O dimensionamento e o desempenho do compressor utilizam rácios de pressão absoluta:
Cálculos da taxa de compressão
Taxa de compressão = Pressão de descarga (abs) ÷ Pressão de aspiração (abs)
Este rácio determina:
- Número de fases de compressão necessárias
- Consumo de energia
- Temperatura de descarga
- Caraterísticas de eficiência
Mapas de desempenho do compressor
Os mapas de desempenho do fabricante utilizam condições de pressão absoluta para uma seleção e funcionamento precisos.
Aplicações de controlo de processos
Muitos sistemas de controlo de processos requerem medições de pressão absoluta:
Cálculos de densidade
Cálculos de densidade de gás para medição e controlo de caudal:
Densidade = (pressão absoluta × peso molecular) ÷ (constante do gás × temperatura absoluta)
Cálculos de transferência de calor
Os cálculos termodinâmicos para permutadores de calor e equipamento de processo utilizam valores absolutos de pressão e temperatura.
Aplicação de processos no mundo real
Recentemente, ajudei Elena, uma engenheira de processos numa fábrica de produtos químicos alemã, com transporte pneumático5 conceção do sistema. O seu sistema transportava pellets de plástico utilizando ar comprimido através de condutas elevadas.
Os cálculos de transporte requerem valores de pressão absoluta para determinar:
- Densidade do ar a várias elevações da conduta
- Cálculos de perdas de carga através de secções verticais
- Requisitos de velocidade do material
- Limitações de capacidade do sistema
A utilização da pressão manométrica teria produzido erros nos cálculos da capacidade de transporte, levando a um equipamento subdimensionado e a um mau desempenho.
Aplicações de controlo de qualidade
O fabrico de precisão requer frequentemente medições de pressão absoluta:
Teste de fugas
As medições de pressão absoluta permitem uma deteção de fugas mais precisa:
Taxa de fuga = Volume × Queda de pressão ÷ Tempo
A utilização da pressão absoluta elimina as variações da pressão atmosférica que afectam as leituras da pressão manométrica.
Padrões de Calibração
Os padrões de calibração da pressão utilizam referências de pressão absoluta para precisão e rastreabilidade.
Como se faz a conversão entre diferentes medições de pressão?
A conversão de pressão entre diferentes sistemas de medição requer a compreensão dos pontos de referência e dos factores de conversão. As conversões exactas evitam erros de cálculo em projectos internacionais.
As conversões de pressão requerem a adição ou subtração da pressão atmosférica quando se muda entre medições absolutas e manométricas, além da aplicação de factores de conversão de unidades. As conversões comuns incluem PSIA para bar, PSIG para kPa e medições de vácuo para pressão absoluta.
Fórmulas básicas de conversão
A relação fundamental entre os tipos de pressão:
Pressão absoluta = pressão manométrica + pressão atmosférica
Pressão manométrica = Pressão absoluta - Pressão atmosférica
Vácuo = Pressão atmosférica - Pressão absoluta
Factores de conversão de unidades
Conversões de unidades de pressão comuns:
| De | Até | Multiplicar por |
|——|—-|———–|
| PSI | bar | 0,06895 |
| bar | PSI | 14.504 |
| PSI | kPa | 6,895 |
| kPa | PSI | 0,1450 |
| PSI | "Hg | 2.036 |
| "Hg | PSI | 0,4912 |
Normas de pressão atmosférica
Valores de pressão atmosférica normalizados para conversões:
| Localização/Padrão | Valor da pressão |
|---|---|
| Nível do mar padrão | 14,696 PSIA, 1,01325 bar |
| Norma de engenharia | 14,7 PSIA, 1,013 bar |
| Padrão métrico | 101,325 kPa, 760 mmHg |
Exemplos de conversão
Conversão de PSIG para PSIA
80 PSIG a PSIA ao nível do mar:
80 PSIG + 14,7 = 94,7 PSIA
Bar Gauge para Bar Absoluto
5 barg para bara ao nível do mar:
5 barg + 1,013 = 6,013 bara
Vácuo para pressão absoluta
25 "Hg de vácuo para PSIA:
14,7 - (25 × 0,4912) = 2,42 PSIA
Considerações sobre a unidade internacional
Os diferentes países utilizam unidades de pressão diferentes:
| Região | Unidades comuns | Atmosférico padrão |
|---|---|---|
| EUA | PSIG, PSIA | 14,7 PSI |
| Europa | bar, kPa | 1,013 bar |
| Ásia | MPa, kgf/cm² | 1,033 kgf/cm² |
| Científico | Pa, kPa | 101,325 kPa |
Considerações sobre a exatidão da conversão
A exatidão da conversão depende dos pressupostos da pressão atmosférica:
Condições standard vs. condições reais
- Padrão: Utiliza uma pressão atmosférica de 14,7 PSI
- Atual: Utiliza a pressão atmosférica local
- Erro: Pode ser de 1-3% consoante o local e as condições climatéricas
Efeitos da temperatura
A pressão atmosférica varia com a temperatura e as condições climatéricas. Para conversões exactas, utilize a pressão atmosférica local real em vez dos valores padrão.
Ferramentas de conversão digital
Os instrumentos de pressão modernos fornecem frequentemente conversões automáticas de unidades. No entanto, a compreensão dos princípios de conversão manual ajuda a verificar as leituras digitais e a resolver erros de conversão.
Aplicação prática da conversão
Trabalhei com Jean-Pierre, um engenheiro de projeto de um fornecedor automóvel francês, nas especificações do sistema pneumático para um projeto global. As suas especificações europeias utilizavam pressão manométrica em bar, mas a instalação na América do Norte exigia valores PSIG.
O processo de conversão envolvido:
- Especificação europeia: 6 barg de pressão de funcionamento
- Converter para absoluto: 6 + 1,013 = 7,013 bara
- Converter unidades: 7,013 × 14,504 = 101,7 PSIA
- Converter para calibre: 101,7 - 14,7 = 87,0 PSIG
Esta abordagem sistemática assegurou especificações de pressão exactas em diferentes sistemas de medição e evitou erros de dimensionamento do equipamento.
Que erros cometem os engenheiros nos cálculos da pressão absoluta?
Os erros de cálculo da pressão absoluta são comuns e podem levar a problemas significativos de desempenho do sistema. A compreensão destes erros ajuda a evitar problemas dispendiosos de conceção e funcionamento.
Os erros comuns de pressão absoluta incluem a utilização da pressão manométrica nos cálculos da lei dos gases, ignorando as variações da pressão atmosférica, conversões incorrectas de unidades e medições de vácuo incorrectas. Estes erros causam normalmente imprecisões no cálculo do 10-30% e problemas de desempenho do sistema.
Utilização da pressão manométrica nos cálculos da lei dos gases
O erro mais comum é utilizar a pressão manométrica em fórmulas que requerem pressão absoluta:
Aplicação incorrecta da lei dos gases
Errado: PV = nRT utilizando a pressão manométrica
Correto: PV = nRT usando pressão absoluta
Este erro gera erros de cálculo proporcionais à pressão atmosférica - aproximadamente 15% ao nível do mar.
Ignorar as variações da pressão atmosférica
Muitos engenheiros assumem uma pressão atmosférica constante de 14,7 PSI independentemente do local ou das condições:
Variações de localização
- Nível do mar: 14,7 PSIA
- Denver (5.280 pés): 12,2 PSIA
- Erro: 17% se estiver a utilizar o valor do nível do mar em Denver
Variações meteorológicas
- Sistema de alta pressão: 15,2 PSIA
- Sistema de baixa pressão: 14,2 PSIA
- Variação: ±3,4% em relação à norma
Conversões incorrectas de unidades
A mistura de unidades de pressão absoluta e manométrica gera erros significativos:
Erros comuns de conversão
- Acrescentar 14,7 às leituras do barómetro (deveria acrescentar 1,013)
- Utilizar 14,7 PSI para locais fora do nível do mar
- Esquecer-se de converter entre absoluto e manómetro ao mudar de unidade
Confusão na medição do vácuo
As medições de vácuo confundem frequentemente os engenheiros porque representam uma pressão inferior à atmosférica:
Relações de pressão de vácuo
- 29 "Hg Vácuo = 0,76 PSIA (e não -29 PSIA)
- Aspiração perfeita = 0 PSIA absoluto
- Pressão atmosférica = Vácuo máximo possível em "Hg
Recentemente, ajudei o Roberto, um engenheiro de projeto de uma empresa de embalagens italiana, a resolver problemas de desempenho do sistema de vácuo. Os seus cálculos mostravam uma capacidade adequada da bomba de vácuo, mas o sistema não conseguia atingir os níveis de vácuo necessários.
O problema era a confusão na medição do vácuo. Roberto calculou os requisitos da bomba utilizando -25 PSIG em vez da pressão absoluta correta de 1,4 PSIA. Este erro fez com que a bomba parecesse 18 vezes mais potente do que a capacidade real.
Erros de compensação de temperatura
Os cálculos da pressão absoluta ignoram frequentemente os efeitos da temperatura:
Requisitos de temperatura da lei dos gases
Os cálculos da lei dos gases requerem a temperatura absoluta (Rankine ou Kelvin):
- Fahrenheit para Rankine: °R = °F + 459,67
- Celsius para Kelvin: K = °C + 273,15
A utilização de temperaturas Fahrenheit ou Celsius nos cálculos da lei dos gases produz erros significativos.
Supervisões de compensação de altitude
Os engenheiros utilizam frequentemente a pressão atmosférica ao nível do mar para instalações a grande altitude:
Erros de pressão de altitude
A 10.000 pés de altitude:
- Atmosférico real: 10.1 PSIA
- Pressuposto do nível do mar: 14,7 PSIA
- Erro: 45% sobreavaliação da pressão absoluta
Erros de cálculo da relação de compressão
Os cálculos da taxa de compressão requerem pressões absolutas, mas os engenheiros utilizam frequentemente pressões manométricas:
Taxa de compressão incorrecta
Para descarga de 80 PSIG, sucção atmosférica:
- Errado: 80 ÷ 0 = indefinido
- Correto: 94.7 ÷ 14.7 = 6.44:1
Erros de cálculo de caudal
Os cálculos de caudal que utilizam diferenciais de pressão requerem valores de pressão absoluta:
Erros de fluxo estrangulado
Cálculos do rácio de pressão crítica:
- Errado: Utilização de rácios de pressão manométrica
- Correto: Utilizar rácios de pressão absoluta
- Impacto: Pode sobrestimar a capacidade de caudal em 15-20%
Erros de conceção do sistema de segurança
O dimensionamento da válvula de segurança requer cálculos de pressão absoluta:
Dimensionamento da válvula de alívio
A capacidade da válvula de alívio depende dos rácios de pressão absoluta. A utilização de pressões manométricas pode resultar em válvulas de alívio subdimensionadas e em riscos de segurança.
Estratégias de prevenção
Evitar erros de cálculo da pressão absoluta através de:
Abordagem sistemática
- Identificar o tipo de pressão necessária: Determinar se o cálculo necessita de pressão absoluta ou manométrica
- Utilizar uma pressão atmosférica correta: Aplicar a pressão atmosférica local e não o nível do mar padrão
- Verificar a coerência da unidade: Assegurar que todas as pressões utilizam o mesmo sistema de unidades
- Dupla verificação das conversões: Verificar os factores de conversão e os pontos de referência
Normas de documentação
- Etiquetar claramente os tipos de pressão: Especificar sempre PSIA, PSIG, bara, barg
- Estado Condições de referência: Documentar os pressupostos da pressão atmosférica
- Incluir tabelas de conversão: Fornecer factores de conversão de referência
Conclusão
A pressão absoluta fornece a imagem completa da pressão essencial para cálculos exactos do sistema pneumático. A compreensão dos princípios da pressão absoluta evita erros de cálculo comuns e assegura um desempenho fiável do sistema de cilindros sem haste em condições de funcionamento variáveis.
Perguntas frequentes sobre a pressão absoluta em sistemas pneumáticos
Qual é a diferença entre pressão absoluta e pressão manométrica?
A pressão absoluta mede a pressão total do vácuo perfeito, enquanto a pressão manométrica mede a pressão acima da atmosférica. A pressão absoluta é igual à pressão manométrica mais a pressão atmosférica (14,7 PSI ao nível do mar).
Porque é que os cálculos pneumáticos requerem pressão absoluta?
As leis dos gases, as equações de fluxo e os cálculos termodinâmicos requerem pressão absoluta porque envolvem rácios de pressão e relações que necessitam de valores de pressão completos. A utilização da pressão manométrica produz erros de cálculo de 10-30%.
Como é que a altitude afecta a pressão absoluta nos sistemas pneumáticos?
A pressão atmosférica diminui cerca de 0,5 PSI por cada 1.000 pés de elevação. Isto reduz a pressão absoluta e pode diminuir a força de saída do cilindro em 3-4% por cada 1.000 pés, a menos que seja compensada através de ajustes de pressão.
Como é que se converte a pressão manométrica em pressão absoluta?
Adicionar a pressão atmosférica à pressão manométrica: PSIA = PSIG + pressão atmosférica. Utilize a pressão atmosférica local (varia com a altitude) em vez da norma de 14,7 PSI para conversões exactas.
O que acontece se utilizarmos a pressão manométrica nos cálculos da pressão absoluta?
A utilização da pressão manométrica em fórmulas que requerem pressão absoluta cria erros proporcionais à pressão atmosférica - tipicamente 15% ao nível do mar. Estes erros podem causar equipamento subdimensionado e um mau desempenho do sistema.
Os cilindros sem haste requerem cálculos de pressão absoluta?
Sim, os cilindros sem haste utilizam as mesmas relações de pressão que os cilindros tradicionais. Os cálculos de força, dimensionamento de caudal e análise de desempenho beneficiam todos dos valores de pressão absoluta, especialmente em aplicações de altitude ou vácuo.
-
Saiba mais sobre o design e as vantagens operacionais dos cilindros pneumáticos sem haste, que são frequentemente utilizados no manuseamento de materiais e na automação. ↩
-
Explorar a Lei do Gás Ideal (PV=nRT), uma equação de estado fundamental que descreve a relação entre pressão, volume e temperatura de um gás. ↩
-
Saiba mais sobre as escalas de temperatura absoluta como Kelvin e Rankine e porque é que são essenciais para os cálculos termodinâmicos e das leis dos gases. ↩
-
Compreender a importância da taxa de compressão no desempenho do compressor e como esta é calculada utilizando pressões absolutas. ↩
-
Descubra como funcionam os sistemas de transporte pneumático para transportar materiais a granel utilizando gás comprimido em processos industriais. ↩




