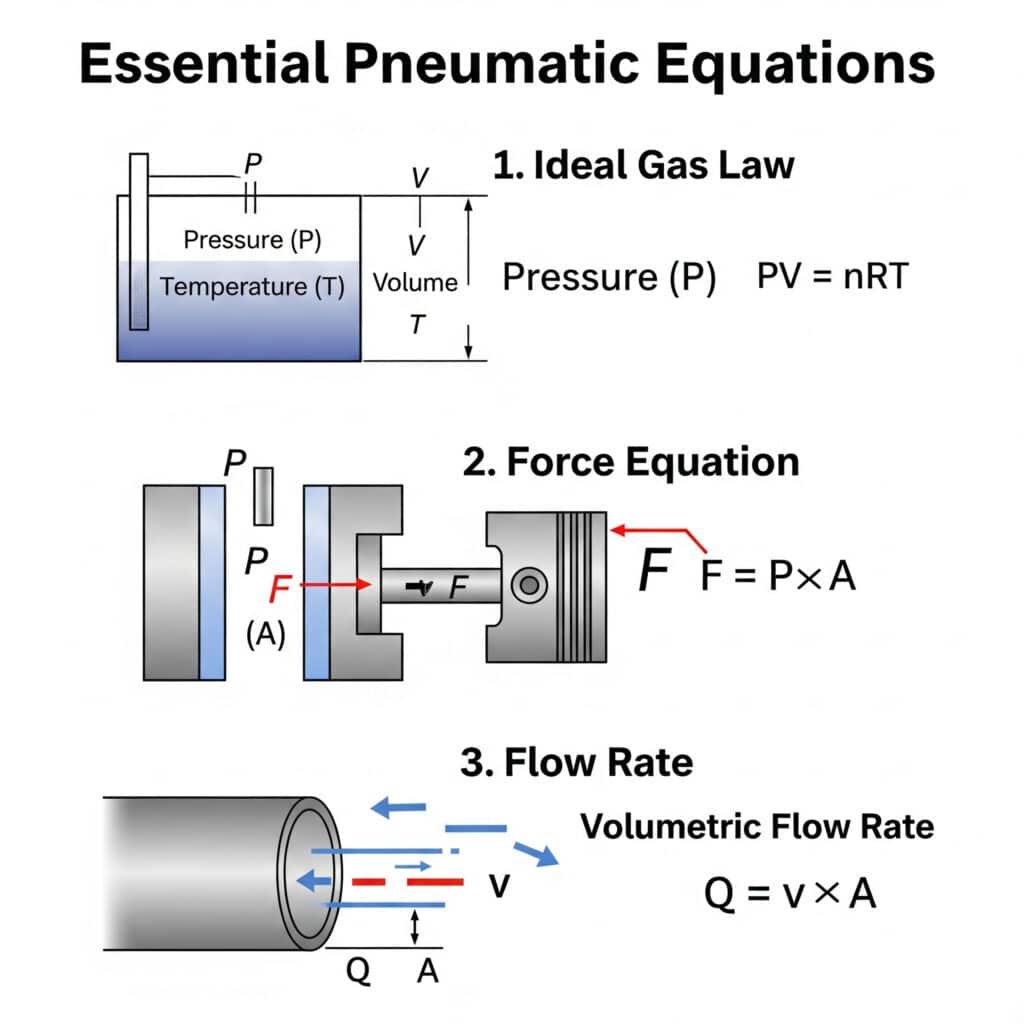
Está constantemente a debater-se com cálculos de sistemas pneumáticos? Muitos engenheiros enfrentam o mesmo problema quando projectam ou resolvem problemas em sistemas pneumáticos. A boa notícia é que o domínio de algumas equações-chave pode resolver a maioria dos seus desafios pneumáticos.
As equações essenciais de transmissão pneumática que todos os engenheiros devem conhecer incluem lei dos gases ideais (PV = nRT)1A equação da força (F = P × A) e a relação do caudal (Q = v × A). A compreensão destes fundamentos permite uma conceção precisa do sistema e a resolução de problemas.
Passei mais de 15 anos a trabalhar com sistemas pneumáticos na Bepto e vi em primeira mão como a compreensão destas equações básicas pode poupar milhares de dólares em tempo de inatividade e evitar erros de conceção dispendiosos.
Índice
- Derivação da equação do gás: Porque é que PV = nRT é importante em sistemas pneumáticos?
- Como é que a força, a pressão e a área se relacionam nos cilindros pneumáticos?
- Qual é a relação entre a taxa de fluxo e a velocidade em sistemas pneumáticos?
- Conclusão
- Perguntas frequentes sobre equações de transmissão pneumática
Derivação da equação do gás: Porque é que PV = nRT é importante em sistemas pneumáticos?
Ao projetar sistemas pneumáticos, é crucial compreender como os gases se comportam em diferentes condições. Este conhecimento pode significar a diferença entre um sistema que funciona de forma fiável e um que falha inesperadamente.
A lei dos gases ideais (PV = nRT) é fundamental para os sistemas pneumáticos porque descreve como a pressão, o volume e a temperatura interagem. Esta relação ajuda os engenheiros a prever como o ar se comportará em cilindros sem haste e outros componentes pneumáticos sob condições de funcionamento variáveis.
A lei dos gases ideais pode parecer um conceito teórico das aulas de física, mas tem aplicações práticas diretas em sistemas pneumáticos. Vou explicar isto em termos mais práticos.
Compreender as variáveis em PV = nRT
| Variável | Significado | Aplicação pneumática |
|---|---|---|
| P | Pressão | Pressão de funcionamento do seu sistema |
| V | Volume | Dimensão da câmara de ar em cilindros |
| n | Número de moles | Quantidade de ar no sistema |
| R | Constante de gás2 | Constante universal (8,314 J/mol-K) |
| T | Temperatura | Temperatura de funcionamento |
Como a temperatura afecta o desempenho pneumático
As variações de temperatura podem afetar significativamente o desempenho do sistema pneumático. No ano passado, um dos nossos clientes na Alemanha, Hans, contactou-me por causa do desempenho inconsistente do seu sistema de cilindros sem haste. O sistema funcionava perfeitamente de manhã, mas perdia potência à tarde.
Depois de analisar a sua configuração, descobrimos que o sistema estava exposto à luz solar direta, causando um aumento de temperatura de 15°C. Utilizando a lei do gás ideal, calculámos que esta mudança de temperatura estava a causar uma variação de pressão de quase 5%. Instalámos um isolamento adequado e o problema foi resolvido imediatamente.
Aplicações práticas da lei dos gases na conceção pneumática
Na conceção de sistemas pneumáticos com cilindros sem hasteA lei dos gases ajuda-nos:
- Calcular as variações de pressão devidas a flutuações de temperatura
- Determinar os requisitos de volume para os reservatórios de ar
- Prever as variações da produção de força em diferentes condições
- Dimensionar os compressores adequadamente para a aplicação
Como é que a força, a pressão e a área se relacionam nos cilindros pneumáticos?
Compreender a relação entre força, pressão e área é essencial para selecionar o cilindro sem haste certo para a sua aplicação. Este conhecimento garante que obtém o desempenho de que necessita sem gastar demasiado.
O relação força-pressão-área3 nos cilindros pneumáticos é definida por F = P × A, em que F é a força (N), P é a pressão (Pa) e A é a área efectiva (m²). Esta equação permite aos engenheiros calcular a força exacta de saída dos cilindros sem haste a diferentes pressões de funcionamento.
Esta equação simples é a base de todos os cálculos de força pneumática, mas existem várias considerações práticas que muitos engenheiros ignoram.
Cálculos da área efectiva para diferentes tipos de cilindros
A área efectiva varia em função do tipo de cilindro:
| Tipo de cilindro | Cálculo da área efectiva | Notas |
|---|---|---|
| De ação simples | A = πr² | Área de furo completo |
| Duplo efeito (extensão) | A = πr² | Área de furo completo |
| Duplo efeito (retração) | A = π(r² - r'²) | r' é o raio da haste |
| Cilindro sem haste | A = πr² | Consistente em ambas as direcções |
Factores de eficiência da força no mundo real
Na prática, a força real produzida é afetada por:
- Perdas por fricção: Tipicamente 3-20%, dependendo do tipo de vedação
- Quedas de pressão: Pode reduzir a pressão efectiva em 5-10%
- Efeitos dinâmicos: As forças de aceleração podem reduzir a força disponível
Lembro-me de trabalhar com a Sarah, uma engenheira mecânica de uma empresa de embalagens no Reino Unido. Ela estava a projetar uma nova máquina e tinha calculado que precisava de um cilindro sem haste com um furo de 63 mm para atingir a força necessária. No entanto, não tinha tido em conta as perdas por fricção.
Recomendámos o aumento para um cilindro com diâmetro de 80 mm, o que proporcionou força adicional suficiente para superar a fricção, mantendo o desempenho exigido. Este simples ajuste poupou-a de uma dispendiosa remodelação após a instalação.
Comparação da produção de força teórica com a real
Ao selecionar cilindros sem haste, recomendo sempre:
- Calcular a força teórica utilizando F = P × A
- Aplicar um fator de segurança de 25% para a maioria das aplicações
- Verificar os cálculos com os dados de desempenho reais do fabricante
- Considerar as condições de carga dinâmica, se aplicável
Qual é a relação entre a taxa de fluxo e a velocidade em sistemas pneumáticos?
O caudal e a velocidade são parâmetros críticos que determinam a rapidez de resposta do seu sistema pneumático. Compreender esta relação ajuda a evitar um desempenho lento e assegura que o seu sistema cumpre os requisitos de tempo de ciclo.
A relação entre caudal (Q) e velocidade (v)4 em sistemas pneumáticos é definida por Q = v × A, em que Q é o caudal volumétrico, v é a velocidade do ar e A é a área da secção transversal da passagem. Esta equação é crucial para o dimensionamento correto das linhas de ar e das válvulas.
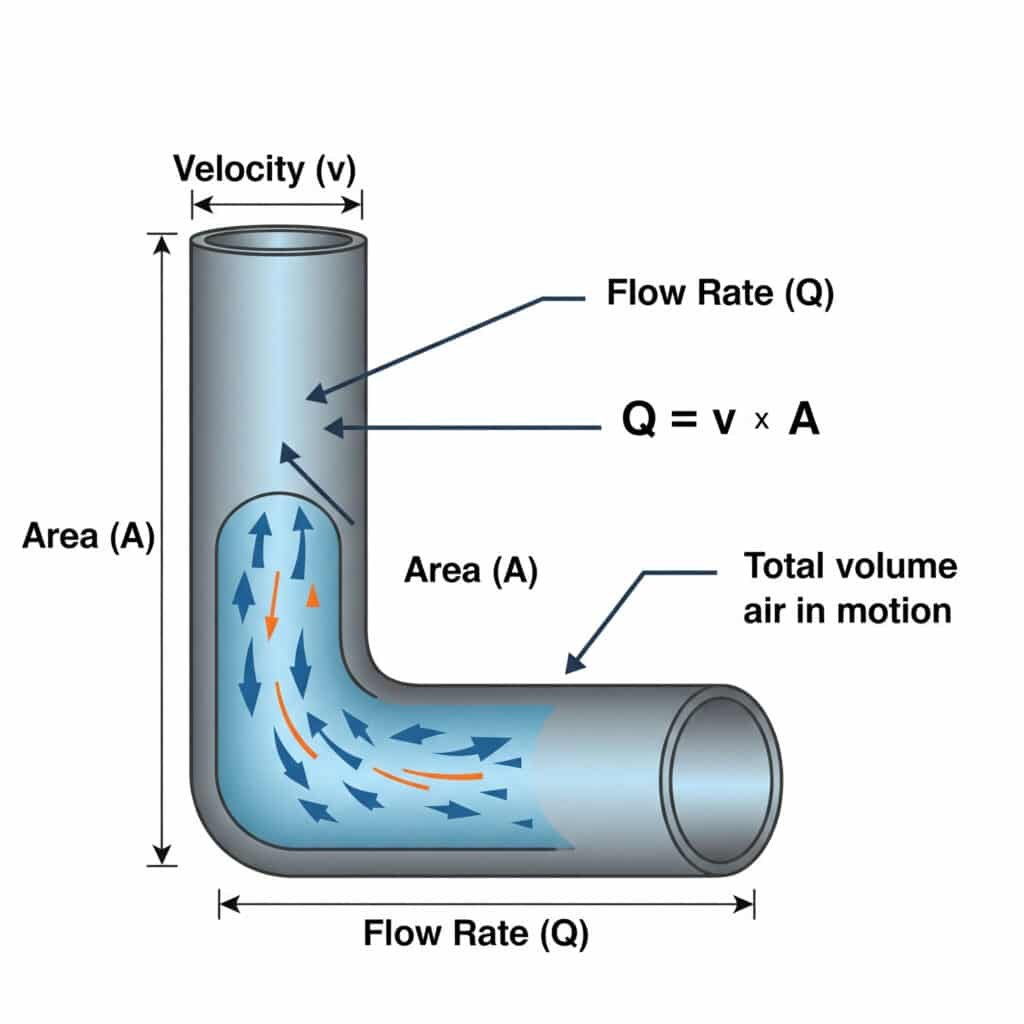
Muitos problemas dos sistemas pneumáticos resultam de um dimensionamento incorreto dos componentes de fornecimento de ar. Vamos explorar como esta equação afecta o desempenho no mundo real.
Caudais críticos para componentes pneumáticos comuns
Diferentes componentes têm diferentes requisitos de caudal:
| Componente | Necessidade de caudal típico | Impacto do subdimensionamento |
|---|---|---|
| Cilindro sem haste (diâmetro de 25 mm) | 15-30 L/min | Funcionamento lento, força reduzida |
| Cilindro sem haste (diâmetro de 63 mm) | 60-120 L/min | Movimento inconsistente |
| Válvula de controlo direcional | Varia consoante o tamanho | Queda de pressão, resposta lenta |
| Unidade de preparação do ar | Total do sistema + 30% | Flutuações de pressão |
Como o diâmetro da tubagem afecta o desempenho do sistema
O diâmetro das suas linhas de ar tem um efeito dramático no desempenho do sistema:
- Queda de pressão: Aumenta com o quadrado da velocidade
- Tempo de resposta: Linhas mais pequenas significam maior velocidade mas maior resistência
- Eficiência energética: Linhas maiores reduzem a queda de pressão mas aumentam o custo
Cálculo de tamanhos de linha adequados para sistemas pneumáticos
Para dimensionar corretamente as linhas de ar para a sua aplicação de cilindro sem haste:
- Determinar o caudal necessário com base no tamanho do cilindro e no tempo de ciclo
- Calcular a queda de pressão máxima admissível (normalmente 0,1 bar ou menos)
- Selecionar o diâmetro da linha que mantenha a velocidade abaixo de 15-20 m/s
- Verificar a capacidade de fluxo da válvula (Valor Cv ou Kv5) corresponde aos requisitos do sistema
Uma vez ajudei um cliente em França que estava a ter um movimento lento do cilindro apesar de ter um grande compressor. O problema não era a geração insuficiente de ar - era que a sua tubagem de 6 mm estava a criar uma resistência excessiva. A atualização para linhas de 10 mm resolveu o problema imediatamente, aumentando a taxa de ciclo da sua máquina em 40%.
Conclusão
A compreensão destas três equações pneumáticas fundamentais - a lei do gás ideal, a relação força-pressão-área e a ligação velocidade-taxa de fluxo - fornece a base para um projeto de sistema pneumático bem sucedido. Ao aplicar estes princípios, pode selecionar os componentes corretos do cilindro sem haste, resolver problemas de forma eficaz e otimizar o desempenho do sistema.
Perguntas frequentes sobre equações de transmissão pneumática
O que é a lei dos gases ideais e porque é que é importante para os sistemas pneumáticos?
A lei do gás ideal (PV = nRT) descreve como a pressão, o volume, a temperatura e a quantidade de gás se relacionam num sistema pneumático. É importante porque ajuda os engenheiros a prever como as condições variáveis (especialmente a temperatura) afectarão o desempenho do sistema e os requisitos de pressão.
Como é que se calcula a força de saída de um cilindro sem haste?
Calcular a força de saída multiplicando a pressão pela área efectiva (F = P × A). Para um cilindro sem haste, a área efectiva é a mesma em ambas as direcções, tornando os cálculos de força mais simples do que nos cilindros convencionais que têm forças de extensão e retração diferentes.
Qual é a diferença entre caudal e velocidade em sistemas pneumáticos?
O caudal é o volume de ar que se move através de um sistema por unidade de tempo (normalmente em L/min), enquanto a velocidade é a velocidade a que o ar se move através de uma passagem (em m/s). Estão relacionados pela equação Q = v × A, em que A é a área da secção transversal da passagem.
Como é que a temperatura afecta o desempenho do sistema pneumático?
A temperatura afecta diretamente a pressão de acordo com a lei dos gases ideais. Um aumento de 10°C na temperatura pode aumentar a pressão em aproximadamente 3,5% se o volume permanecer constante. Isto pode causar variações de pressão, afetar o desempenho dos vedantes e alterar a força de saída em cilindros sem haste.
Qual é a causa mais comum de queda de pressão em sistemas pneumáticos?
As causas mais comuns de queda de pressão são linhas de ar subdimensionadas, conexões restritivas e capacidade inadequada do fluxo da válvula. De acordo com a equação do caudal, passagens mais pequenas requerem maior velocidade do ar, o que aumenta exponencialmente a resistência e a queda de pressão.
Como dimensionar corretamente as linhas de ar para um cilindro sem haste?
Dimensione as linhas de ar calculando o caudal necessário com base no volume do cilindro e no tempo de ciclo, depois selecione um diâmetro de linha que mantenha a velocidade do ar abaixo dos 15-20 m/s para minimizar a queda de pressão. Para a maioria das aplicações de cilindros sem haste, as linhas de 8-12 mm proporcionam um bom equilíbrio entre desempenho e custo.
-
Fornece uma explicação pormenorizada da lei dos gases ideais, a equação de estado fundamental para um gás ideal hipotético que aproxima o comportamento de muitos gases em várias condições. ↩
-
Explica o papel e o valor da constante universal dos gases (R) na lei dos gases ideais, que funciona como uma constante física que liga as escalas de energia às escalas de temperatura. ↩
-
Oferece uma explicação fundamental da pressão, definida como a força aplicada perpendicularmente à superfície de um objeto por unidade de área sobre a qual essa força é distribuída. ↩
-
Detalha o princípio da equação da continuidade, um conceito fundamental na dinâmica dos fluidos que afirma que, para um fluido incompressível, a taxa de fluxo de massa deve ser constante de uma secção transversal de um tubo para outra. ↩
-
Fornece uma definição técnica do Coeficiente de Caudal (Cv) e do Fator de Caudal (Kv), que são valores normalizados utilizados para comparar as capacidades de caudal de diferentes válvulas. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська