การต้านทานการไหลส่งผลต่อประสิทธิภาพของระบบนิวเมติกของคุณอย่างไร?

คุณกำลังประสบปัญหาความเร็วของกระบอกสูบช้า การเคลื่อนไหวไม่สม่ำเสมอ หรือแรงไม่เพียงพอในระบบนิวแมติกของคุณหรือไม่? ปัญหาเหล่านี้มักเกิดจากสาเหตุที่มักถูกเข้าใจผิด: ความต้านทานการไหล วิศวกรหลายคนมักเลือกขนาดของชิ้นส่วนนิวแมติกโดยพิจารณาจากความต้องการด้านแรงดันและแรงเท่านั้น โดยมองข้ามผลกระทบที่สำคัญของความต้านทานการไหลต่อประสิทธิภาพการใช้งานจริง.

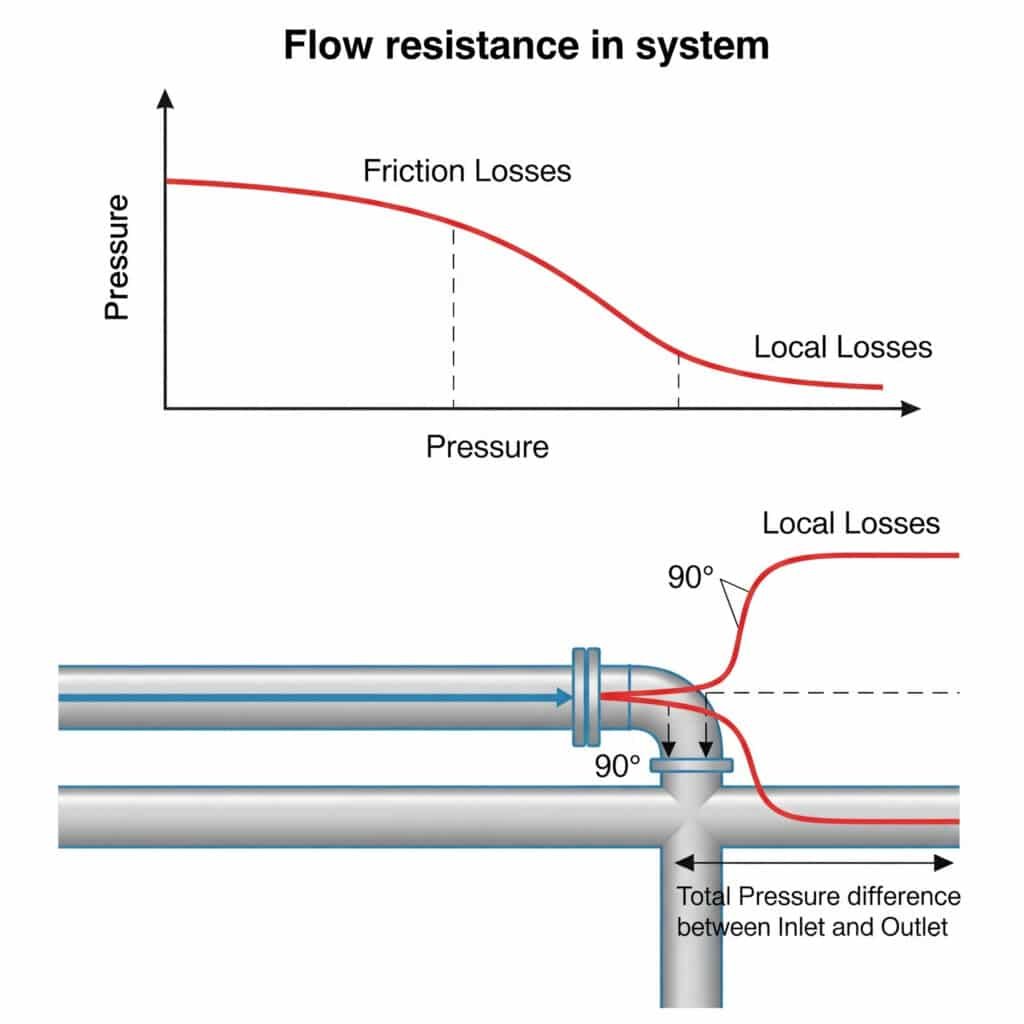
ความต้านทานการไหลในระบบนิวเมติกส์ทำให้เกิดการลดความดันซึ่งลดกำลังที่มีอยู่ จำกัดความเร็วสูงสุด และทำให้เกิดการเคลื่อนไหวที่ไม่สม่ำเสมอ ความต้านทานนี้เกิดจากทั้งแรงเสียดทานตามท่อตรง (การสูญเสียจากแรงเสียดทาน) และการรบกวนที่ข้อต่อ ท่อโค้ง และวาล์ว (การสูญเสียในท้องถิ่น) ความต้านทานเหล่านี้รวมกันสามารถลดประสิทธิภาพการทำงานของระบบจริงได้ถึง 20-50% เมื่อเทียบกับการคำนวณทางทฤษฎี.

ตลอดระยะเวลา 15 ปีที่ทำงานกับระบบนิวเมติกส์ที่ Bepto ผมได้พบเห็นกรณีมากมายที่ความเข้าใจและการแก้ไขปัญหาความต้านทานการไหลสามารถเปลี่ยนระบบที่ทำงานได้ไม่ดีให้กลายเป็นระบบที่เชื่อถือได้และมีประสิทธิภาพ ผมขอแบ่งปันสิ่งที่ผมได้เรียนรู้เกี่ยวกับการคำนวณและลดปัจจัยที่ซ่อนเร้นเหล่านี้ซึ่งเป็นตัวทำลายประสิทธิภาพ.

สารบัญ

• คุณคำนวณการสูญเสียแรงเสียดทานในท่อลมอย่างไร?
• ทำไมวิธีการความยาวเทียบเท่าจึงมีความสำคัญต่อการออกแบบระบบอย่างแม่นยำ?
• เกิดอะไรขึ้นเมื่ออากาศไหลผ่านส่วนที่มีขนาดรูเล็กลง?
• สรุป
• คำถามที่พบบ่อยเกี่ยวกับความต้านทานการไหลในระบบนิวเมติก

คุณคำนวณการสูญเสียแรงเสียดทานในท่อลมอย่างไร?

การสูญเสียแรงเสียดทานในท่อและท่อตรงเป็นพื้นฐานของการคำนวณความต้านทานการไหล แต่หลายวิศวกรพึ่งพาหลักการง่ายๆ ที่เกินจริงซึ่งนำไปสู่ระบบที่มีขนาดเล็กเกินไป.

การสูญเสียแรงเสียดทานในท่อลมถูกคำนวณโดยใช้ สมการดาร์ซี-ไวส์บาค¹: ΔP = λ(L/D)(ρv²/2) โดยที่ λ คือค่าสัมประสิทธิ์แรงเสียดทาน, L คือความยาวของท่อ, D คือเส้นผ่านศูนย์กลางของท่อ, ρ คือความหนาแน่นของอากาศ และ v คือความเร็วของการไหล สำหรับระบบนิวเมติก ค่าสัมประสิทธิ์แรงเสียดทาน λ จะเปลี่ยนแปลงตาม เรย์โนลด์นัมเบอร์² และความหยาบสัมพัทธ์ และโดยทั่วไปจะถูกกำหนดโดยใช้ตารางค้นหาหรือ แผนภาพมูดี้³.

การเข้าใจการสูญเสียแรงเสียดทานมีผลกระทบในทางปฏิบัติต่อการออกแบบระบบและการแก้ไขปัญหา. ให้ผมอธิบายให้เข้าใจเป็นข้อมูลที่สามารถนำไปใช้ได้.

การใช้ตารางปัจจัยแรงเสียดทานอย่างมีประสิทธิภาพ

ค่าสัมประสิทธิ์แรงเสียดทาน (λ) เป็นพารามิเตอร์สำคัญในการคำนวณการลดความดัน แต่การกำหนดค่าของมันต้องพิจารณาเงื่อนไขการไหล:

ระบอบการไหล	เรย์โนลด์ส หมายเลข (Re)	การหาค่าสัมประสิทธิ์แรงเสียดทาน
การไหลแบบลามินาร์	น้อยกว่า < 2000	λ = 64/Re
การไหลแบบเปลี่ยนผ่าน	2000 < Re < 4000	ไม่น่าเชื่อถือ – หลีกเลี่ยงการออกแบบในช่วงนี้
การไหลแบบปั่นป่วน	Re > 4000	ใช้ตารางค้นหาที่อิงตามความขรุขระสัมพัทธ์ (ε/D)

ตารางค้นหาค่าสัมประสิทธิ์แรงเสียดทานเชิงปฏิบัติ

สำหรับการไหลแบบปั่นป่วนในระบบนิวเมติก ให้ใช้ตารางที่ง่ายนี้:

วัสดุท่อ	ความขรุขระสัมพัทธ์ (ε/D)	ปัจจัยแรงเสียดทาน (λ) ที่ค่าเรย์โนลด์สทั่วไป
		Re = 10,000
ท่อเรียบ (PVC, โพลียูรีเทน)	0.0001 – 0.0005	0.031
ท่ออลูมิเนียม	0.001 – 0.002	0.035
เหล็กชุบสังกะสี	0.003 – 0.005	0.042
เหล็กเป็นสนิม	0.01 – 0.05	0.054

การคำนวณการลดความดันในระบบนิวเมติกส์จริง

มาดูตัวอย่างในทางปฏิบัติกัน:

พารามิเตอร์	มูลค่า/การคำนวณ	ตัวอย่าง
เส้นผ่านศูนย์กลางของท่อ (D)	เส้นผ่านศูนย์กลางภายใน	8 มิลลิเมตร (0.008 เมตร)
ความยาวท่อ (L)	ความยาวตรงทั้งหมด	5 เมตร
อัตราการไหล (Q)	จากข้อกำหนดของระบบ	20 ลิตรมาตรฐานต่อวินาที
ความหนาแน่นของอากาศ (ρ)	ที่ความดันในการทำงาน	7.2 กิโลกรัมต่อลูกบาศก์เมตร ที่ 6 บาร์
ความเร็วการไหล (v)	v = Q/(π×D²/4)	v = 0.02 ลูกบาศก์เมตร/วินาที/(π×0.008²/4) = 398 เมตร/วินาที
เรย์โนลด์ส หมายเลข (Re)	Re = ρvD/μ	Re = 7.2×398×0.008/1.8×10⁻⁵ = 1,273,600
ความขรุขระสัมพัทธ์	สำหรับท่อโพลียูรีเทน	0.0003
ค่าสัมประสิทธิ์แรงเสียดทาน (λ)	จากตารางค้นหา	0.017
การลดความดัน (ΔP)	ΔP = λ(L/D)(ρv²/2)	ΔP = 0.017×(5/0.008)×(7.2×398²/2) = 6.07 บาร์

การประยุกต์ใช้ในโลกจริง: แก้ไขปัญหาความเร็วของกระบอกสูบ

ปีที่แล้ว ฉันได้ทำงานร่วมกับซาร่าห์ วิศวกรการผลิตที่บริษัทอุปกรณ์บรรจุภัณฑ์ในวิสคอนซิน ระบบกระบอกสูบไร้ก้านของเธอทำงานได้เพียง 60% ของความเร็วที่คาดหวังไว้ แม้ว่าจะมีกระบอกสูบที่มีขนาดถูกต้องและแรงดันจ่ายเพียงพอแล้วก็ตาม.

หลังจากวิเคราะห์ระบบของเธอแล้ว ฉันพบว่าเธอใช้ท่อขนาด 6 มม. สำหรับการใช้งานที่ต้องการการไหลสูง การสูญเสียแรงเสียดทานทำให้แรงดันลดลง 2.1 บาร์ ซึ่งลดแรงและความเร็วที่มีอยู่ลงอย่างมาก เมื่อเราอัพเกรดเป็นท่อขนาด 10 มม. เราสามารถลดการลดลงของแรงดันเหลือ 0.4 บาร์ และระบบของเธอก็สามารถทำงานได้ตามที่ต้องการทันทีโดยไม่ต้องมีการเปลี่ยนแปลงอื่นใด.

ปัจจัยที่มีผลต่อการสูญเสียแรงเสียดทานในระบบจริง

หลายปัจจัยมีอิทธิพลต่อการสูญเสียแรงเสียดทานจริง:

1. อุณหภูมิอากาศ: อุณหภูมิที่สูงขึ้นเพิ่มความหนืดและแรงเสียดทาน
2. การปนเปื้อน: สิ่งสกปรกและน้ำมันสามารถเพิ่มความหยาบเชิงประสิทธิภาพ
3. การดัดท่อ: การเปลี่ยนรูปขนาดเล็กในท่อโค้งเพิ่มแรงต้านทาน
4. การเสื่อมสภาพตามอายุ: การกัดกร่อนและการสะสมของคราบเพิ่มความขรุขระเมื่อเวลาผ่านไป
5. ความดันในการทำงาน: แรงดันที่สูงขึ้นเพิ่มความหนาแน่นและการสูญเสีย

ทำไมวิธีการความยาวเทียบเท่าจึงมีความสำคัญต่อการออกแบบระบบอย่างแม่นยำ?

การสูญเสียในท้องถิ่นที่ข้อต่อ, วาล์ว, และข้อโค้งมักเกินการสูญเสียแรงเสียดทานในท่อตรง แต่ยังคงมีวิศวกรจำนวนมากที่ละเลยหรือใช้วิธีการประมาณการหยาบๆ ซึ่งนำไปสู่ปัญหาด้านประสิทธิภาพ.

วิธีการเทียบความยาวจะแปลงการสูญเสียในท้องถิ่นจากข้อต่อและวาล์วให้เป็นความยาวของท่อตรงที่เทียบเท่าซึ่งจะก่อให้เกิดการลดแรงดันเท่ากัน การคำนวณนี้ใช้สูตร Le = K(D/λ) โดยที่ Le คือความยาวเทียบเท่า, K คือ สัมประสิทธิ์การสูญเสียในท้องถิ่น⁴, D คือเส้นผ่านศูนย์กลางของท่อ และ λ คือค่าสัมประสิทธิ์ความเสียดทาน วิธีนี้ช่วยให้การคำนวณง่ายขึ้นและให้การคาดการณ์ประสิทธิภาพของระบบที่แม่นยำยิ่งขึ้น.

มาสำรวจวิธีการนำวิธีนี้ไปใช้อย่างมีประสิทธิภาพในการออกแบบระบบนิวเมติกกัน.

ตารางความยาวเทียบเท่าสำหรับชิ้นส่วนระบบนิวเมติกทั่วไป

นี่คือตารางอ้างอิงเชิงปฏิบัติสำหรับส่วนประกอบนิวเมติกส์ทั่วไป:

องค์ประกอบ	ค่า K	ความยาวเทียบเท่า (Le/D)
ข้อศอก 90° (คม)	0.9	30
ข้อศอก 90° (รัศมีมาตรฐาน)	0.3	10
ข้อศอก 45 องศา	0.2	7
ทางแยกตัวที (การไหลผ่าน)	0.3	10
ทางแยกตัวที (การไหลแยก)	1.0	33
วาล์วลูกบอล (เปิดเต็มที่)	0.1	3
วาล์วประตู (เปิดเต็มที่)	0.2	7
ข้อต่อเชื่อมต่อด่วน	0.4-0.8	13-27
วาล์วกันกลับ	1.5-2.5	50-83
วาล์วควบคุมการไหลมาตรฐาน	1.0-3.0	33-100

การใช้วิธีความยาวเทียบเท่า

เพื่อใช้วิธีนี้อย่างมีประสิทธิภาพ:

1. ระบุส่วนประกอบทั้งหมดในวงจรนิวเมติกของคุณ
2. หาค่า K-value หรืออัตราส่วนความยาวเทียบเท่า (Le/D) สำหรับแต่ละองค์ประกอบ
3. คำนวณความยาวเทียบเท่าโดยการคูณด้วยเส้นผ่านศูนย์กลางของท่อ
4. เพิ่มทุกความยาวที่เท่ากันเข้ากับความยาวท่อตรงจริง
5. ใช้ความยาวรวมที่มีประสิทธิภาพในการคำนวณการสูญเสียแรงเสียดทานของคุณ

ตัวอย่างเช่น ระบบที่มีท่อตรงขนาด 8 มม. ยาว 5 เมตร พร้อมข้อศอก 90° สี่ตัว, ข้อต่อสามทางหนึ่งตัว และข้อต่อเร็วสองตัว:

องค์ประกอบ	ปริมาณ	Le/D	ความยาวเทียบเท่า
ข้อศอก 90°	4	10	4 × 10 × 0.008ม. = 0.32ม.
ทางแยกสามแยก	1	10	1 × 10 × 0.008 เมตร = 0.08 เมตร
ตัวเชื่อมต่อแบบเร็ว	2	20	2 × 20 × 0.008ม = 0.32ม
ความยาวเทียบเท่าทั้งหมด			0.72 เมตร
ความยาวตรงจริง			5.00 เมตร
ความยาวรวมที่มีประสิทธิภาพ			5.72 เมตร

นี่หมายความว่า ระบบ 5 เมตรของคุณทำงานเหมือนระบบ 5.72 เมตรจริง ๆ เนื่องจากความสูญเสียในท้องถิ่น—ความยาวที่มีประสิทธิภาพเพิ่มขึ้น 14.4%.

กรณีศึกษา: การเพิ่มประสิทธิภาพการจัดวางวาล์วในระบบประกอบ

เมื่อเร็ว ๆ นี้ ผมได้ช่วยเหลือมิเกล วิศวกรระบบอัตโนมัติที่โรงงานประกอบอิเล็กทรอนิกส์ในรัฐแอริโซนา ระบบหยิบและวางของเขาประสบปัญหาการเคลื่อนไหวที่ไม่สม่ำเสมอและความแปรปรวนของเวลาในการทำงาน แม้ว่าจะใช้ชิ้นส่วนคุณภาพสูงก็ตาม.

การวิเคราะห์พบว่าท่อรวมวาล์วของเขาอยู่ห่างจากกระบอกสูบ 3 เมตร และวงจรประกอบด้วยข้อต่อจำนวนมาก การคำนวณความยาวเทียบเท่าแสดงให้เห็นว่าระยะทางจริง 3 เมตรของเขามีความยาวที่มีประสิทธิภาพ 7.2 เมตร เนื่องจากการสูญเสียในท้องถิ่น—มากกว่าสองเท่าของระยะทางท่อตรง!

โดยการย้ายตำแหน่งของวาล์วแมนิโฟลด์ให้ใกล้กับกระบอกสูบมากขึ้นและกำจัดข้อต่อหลายจุด เราสามารถลดความยาวที่มีผลจริงจาก 7.2 เมตร เหลือเพียง 2.1 เมตร ซึ่งช่วยลดการตกของแรงดันได้ถึง 70% ส่งผลให้การทำงานมีความสม่ำเสมอและลดเวลาในการทำงานต่อรอบได้ 15%.

คำแนะนำที่เป็นประโยชน์เพื่อลดการสูญเสียในท้องถิ่น

เพื่อลดการสูญเสียในท้องถิ่นในระบบนิวเมติกของคุณ:

1. ใช้ข้อศอกแบบโค้งหรือมน แทนที่จะเป็นโค้งหักศอก (ลดค่า K ลง 67%)
2. ลดจำนวนข้อต่อให้น้อยที่สุด โดยการวางแผนเส้นทางที่ตรงมากขึ้น
3. เลือกส่วนประกอบที่มีข้อจำกัดต่ำ เช่น วาล์วลูกบอลแบบเต็มเส้นผ่านศูนย์กลางเมื่อเหมาะสม
4. ปรับขนาดให้เหมาะสม – ข้อต่อขนาดเล็กเกินไปทำให้เกิดการสูญเสียที่ไม่สมส่วน
5. ติดตั้งวาล์วให้อยู่ใกล้กับตัวกระตุ้น เพื่อลดความยาวของท่อที่มีผลจริงให้น้อยที่สุด

เกิดอะไรขึ้นเมื่ออากาศไหลผ่านส่วนที่มีขนาดรูเล็กลง?

ส่วนที่มีเส้นผ่านศูนย์กลางลดลงในวงจรนิวเมติก เช่น วาล์วที่ปิดบางส่วน ข้อต่อที่มีขนาดเล็กกว่า หรือจุดเปลี่ยนขนาดเส้นผ่านศูนย์กลาง ก่อให้เกิดข้อจำกัดในการไหลอย่างมีนัยสำคัญ ซึ่งอาจส่งผลกระทบอย่างรุนแรงต่อประสิทธิภาพของระบบ.

เมื่ออากาศไหลผ่านส่วนที่มีขนาดรูเล็กลง, แรงดันลดลง⁵ เกิดขึ้นตามสูตร ΔP = ρ(v₂² – v₁²)/2 โดยที่ v₁ คือความเร็วก่อนการจำกัด และ v₂ คือความเร็วในบริเวณที่มีการจำกัด ซึ่งสามารถชดเชยได้โดยใช้ปัจจัยชดเชยอัตราส่วนของรูเจาะ C = (1 – (d/D)⁴) โดยที่ d คือเส้นผ่านศูนย์กลางที่ลดลง และ D คือเส้นผ่านศูนย์กลางเดิม ปัจจัยนี้ช่วยในการทำนายประสิทธิภาพของระบบจริงและหลีกเลี่ยงการเลือกขนาดชิ้นส่วนที่เล็กเกินไป.

มาสำรวจผลกระทบในทางปฏิบัติของการลดขนาดรูเจาะและวิธีการนำมาพิจารณาในการออกแบบระบบ.

การคำนวณการลดความดันที่จุดเปลี่ยนขนาดเส้นผ่านศูนย์กลาง

เมื่ออากาศไหลจากเส้นผ่านศูนย์กลางที่ใหญ่กว่าไปยังเส้นผ่านศูนย์กลางที่เล็กกว่า ความดันที่ลดลงสามารถคำนวณได้โดยใช้:

พารามิเตอร์	สูตร	ตัวอย่าง
เส้นผ่านศูนย์กลางเดิม (D)	จากข้อมูลจำเพาะ	10 มิลลิเมตร
เส้นผ่านศูนย์กลางที่ลดลง (d)	จากข้อมูลจำเพาะ	6 มิลลิเมตร
อัตราส่วนรูเจาะ (d/D)	การหารแบบง่าย	0.6
อัตราการไหล (Q)	จากข้อกำหนดของระบบ	15 ลิตรมาตรฐานต่อวินาที
ความเร็วในท่อเดิม (v₁)	v₁ = Q/(π×D²/4)	191 เมตรต่อวินาที
ความเร็วในส่วนที่ลดลง (v₂)	v₂ = Q/(π×d²/4)	531 เมตรต่อวินาที
การลดความดัน (ΔP)	ΔP = ρ(v₂² – v₁²)/2	0.88 บาร์
ปัจจัยชดเชย (C)	C = (1 – (d/D)⁴)	0.87

สถานการณ์ทั่วไปของการลดขนาดรูเจาะและผลกระทบ

นี่คือวิธีที่การลดขนาดรูต่างๆ ส่งผลต่อความสามารถในการไหล:

การลดขนาดรู	การลดกำลังการไหล	การเพิ่มขึ้นของความดันตกคร่อม
10 มม. ถึง 8 มม.	36%	2.4 เท่า
10 มม. ถึง 6 มม.	64%	7.7×
10 มม. ถึง 4 มม.	84%	39×
8 มม. ถึง 6 มม.	44%	3.2 เท่า
8 มม. ถึง 4 มม.	75%	16×
6 มม. ถึง 4 มม.	56%	5.1×

ตัวเลขเหล่านี้ชี้ให้เห็นว่าทำไมการลดขนาดเส้นผ่าศูนย์กลางที่ดูเหมือนเล็กน้อยสามารถมีผลกระทบอย่างรุนแรงต่อประสิทธิภาพของระบบ.

ผลกระทบสะสมจากการจำกัดหลายประการ

ในวงจรนิวเมติกจริง จะมีการจำกัดหลายประการเกิดขึ้นต่อเนื่องกัน ผลของข้อจำกัดเหล่านี้จะสะสมกันและสามารถคำนวณได้โดยใช้:

1. แปลงข้อจำกัดแต่ละข้อให้เป็นค่า C-factor ที่เทียบเท่า
2. คำนวณค่า C-factor รวม: Ctotal = 1 – (1-C₁)(1-C₂)(1-C₃)…
3. ใช้ปัจจัยรวมนี้เพื่อกำหนดการลดลงของประสิทธิภาพโดยรวมของระบบ

กรณีศึกษา: การแก้ไขปัญหาความไม่สอดคล้องระหว่างวาล์วและตัวกระตุ้น

เมื่อเดือนที่แล้ว ผมได้ทำงานร่วมกับโธมัส ผู้จัดการฝ่ายบำรุงรักษาที่โรงงานผลิตเฟอร์นิเจอร์ในรัฐนอร์ทแคโรไลนา ระบบกระบอกสูบไร้ก้านใหม่ของเขาทำงานด้วยความเร็วน้อยกว่าครึ่งหนึ่งของความเร็วที่คาดไว้ แม้ว่าจะใช้ขนาดวาล์วตามที่ผู้ผลิตแนะนำก็ตาม.

การสืบสวนพบว่ามีการลดขนาดรูหลายจุดในวงจรของเขา:

• สายจ่ายขนาด 10 มม. ไปยังพอร์ตวาล์วขนาด 8 มม. (C₁ = 0.36)
• พอร์ตวาล์วขนาด 8 มม. ไปยังข้อต่อขนาด 6 มม. (C₂ = 0.44)
• ข้อต่อขนาด 6 มม. ไปยังพอร์ตกระบอกสูบขนาด 8 มม. พร้อมข้อจำกัดภายใน (C₃ = 0.32)

ปัจจัยการชดเชยทั้งหมดคือ Ctotal = 1 – (1-0.36)(1-0.44)(1-0.32) = 0.75 ซึ่งหมายความว่า ระบบของเขาสูญเสียความสามารถในการไหลตามทฤษฎีไป 75%!

โดยการอัปเกรดส่วนประกอบให้มีขนาดที่เหมาะสมทั่วทั้งระบบ เราสามารถขจัดข้อจำกัดเหล่านี้และบรรลุประสิทธิภาพที่ต้องการได้โดยไม่ต้องเปลี่ยนกระบอกสูบหรือแรงดันจ่าย.

กลยุทธ์เชิงปฏิบัติเพื่อลดการสูญเสียจากการบีบอัด

เพื่อลดการสูญเสียจากการลดขนาดบ่อ:

1. กำหนดขนาดส่วนประกอบอย่างสม่ำเสมอ ตลอดวงจรนิวเมติก
2. ใช้ขนาดท่อที่ใหญ่ที่สุดเท่าที่สามารถใช้งานได้จริง สำหรับการใช้งานที่ต้องการการไหลสูง
3. โปรดให้ความสนใจกับข้อจำกัดของส่วนประกอบภายใน, ไม่ใช่แค่ขนาดของสายเชื่อมต่อ
4. พิจารณาเส้นทางการไหลขนาน สำหรับความต้องการการไหลสูง
5. กำจัดอะแดปเตอร์และการเปลี่ยนผ่านที่ไม่จำเป็น เท่าที่จะเป็นไปได้

หลักการ “จุดอ่อนที่สุด” ในระบบนิวเมติกส์

โปรดจำไว้ว่าประสิทธิภาพของระบบนิวเมติกของคุณถูกจำกัดโดยส่วนประกอบที่มีข้อจำกัดมากที่สุด ส่วนประกอบเพียงชิ้นเดียวที่มีขนาดเล็กเกินไปสามารถลบล้างประโยชน์ของส่วนประกอบที่มีขนาดเหมาะสมในส่วนอื่น ๆ ของระบบได้.

ตัวอย่างเช่น ระบบที่มีท่อขนาด 10 มม., วาล์วขนาด 10 มม., แต่ข้อต่อขนาด 6 มม. ที่กระบอกสูบ จะทำงานได้เหมือนกับระบบที่มีชิ้นส่วนขนาด 6 มม. ทั้งหมด—แต่มีค่าใช้จ่ายสูงกว่า.

สรุป

การเข้าใจและคำนวณความต้านทานการไหลอย่างถูกต้อง—ผ่านตารางค่าสัมประสิทธิ์แรงเสียดทาน, วิธีการความยาวเทียบเท่า, และการชดเชยรูรับแสงที่ลดลง—เป็นสิ่งจำเป็นสำหรับการออกแบบระบบนิวเมติกส์ที่ทำงานได้ตามที่คาดหวังในสภาพแวดล้อมจริง ด้วยการประยุกต์ใช้วิธีการคำนวณและหลักการออกแบบเหล่านี้ คุณสามารถเพิ่มประสิทธิภาพการใช้งานกระบอกสูบไร้ก้านและระบบนิวเมติกส์อื่น ๆ ให้ได้สูงสุดทั้งในด้านประสิทธิภาพและความน่าเชื่อถือ.

คำถามที่พบบ่อยเกี่ยวกับความต้านทานการไหลในระบบนิวเมติก

1. ให้รายละเอียดการแยกย่อยอย่างละเอียดของสมการดาร์ซี-ไวส์บาค ซึ่งเป็นสูตรพื้นฐานและใช้กันอย่างแพร่หลายในพลศาสตร์ของไหล สำหรับการคำนวณการสูญเสียความดันเนื่องจากแรงเสียดทานในท่อ. ↩

2. ให้คำนิยามที่ชัดเจนของจำนวนเรย์โนลด์ ซึ่งเป็นปริมาณไม่มีมิติที่สำคัญใช้ในการทำนายรูปแบบการไหล (ไหลแบบชั้นเดียวหรือไหลแบบปั่นป่วน) ในสถานการณ์การไหลของของไหลที่แตกต่างกัน. ↩

3. นำเสนอแผนภาพมูดี้ ซึ่งเป็นกราฟที่ครอบคลุมที่แสดงค่าสัมประสิทธิ์แรงเสียดทานดาร์ซีเทียบกับตัวเลขเรย์โนลด์และความขรุขระสัมพัทธ์ ซึ่งเป็นเครื่องมือมาตรฐานสำหรับวิศวกรในการกำหนดความดันตกคร่อมในท่อ. ↩

4. อธิบายแนวคิดของค่า K หรือสัมประสิทธิ์การสูญเสียในท้องถิ่น ซึ่งเป็นตัวเลขที่ไม่มีหน่วย ใช้เพื่ออธิบายการสูญเสียความดันในข้อต่อท่อหรือวาล์ว เป็นส่วนหนึ่งของวิธีการความยาวเทียบเท่า. ↩

5. รายละเอียดฟิสิกส์เบื้องหลังการลดความดันที่เกิดขึ้นเมื่อของไหลผ่านช่องทางที่จำกัด (รูเปิด) โดยอิงตามหลักการของสมการความต่อเนื่องและหลักการของแบร์นูลลี. ↩