Pressure measurements confuse even experienced engineers. I’ve troubleshot countless pneumatic systems where incorrect pressure references caused performance issues. Understanding absolute pressure prevents costly calculation errors and system failures.
Absolute pressure (ABS pressure) measures pressure relative to a perfect vacuum, including atmospheric pressure in the measurement. It equals gauge pressure plus atmospheric pressure (14.7 PSI at sea level), providing the true total pressure acting on pneumatic components.
Last week, I helped Thomas, a design engineer from a Dutch manufacturing company, resolve altitude-related performance issues with his rodless pneumatic cylinder1 system. His calculations worked perfectly at sea level but failed at their mountain facility. The problem wasn’t equipment failure – it was absolute pressure misconceptions.
Table of Contents
- What is Absolute Pressure and How Does It Differ from Gauge Pressure?
- Why is Absolute Pressure Critical for Pneumatic Calculations?
- How Does Altitude Affect Absolute Pressure in Pneumatic Systems?
- What Are the Common Applications of Absolute Pressure in Industrial Settings?
- How Do You Convert Between Different Pressure Measurements?
- What Mistakes Do Engineers Make with Absolute Pressure Calculations?
What is Absolute Pressure and How Does It Differ from Gauge Pressure?
Absolute pressure represents the total pressure acting on a system, measured from a perfect vacuum reference point. This measurement includes atmospheric pressure effects that gauge pressure ignores.
Absolute pressure equals gauge pressure plus atmospheric pressure. At sea level, atmospheric pressure is 14.7 PSI, so 80 PSIG gauge pressure equals 94.7 PSIA absolute pressure. This distinction is crucial for accurate pneumatic system calculations.

Understanding Pressure Reference Points
Different pressure measurements use different reference points:
| Pressure Type | Reference Point | Symbol | Typical Range |
|---|---|---|---|
| Absolute | Perfect Vacuum | PSIA | 0 to 1000+ PSIA |
| Gauge | Atmospheric | PSIG | -14.7 to 1000+ PSIG |
| Differential | Between Two Points | PSID | Variable |
| Vacuum | Below Atmospheric | “Hg | 0 to 29.92 “Hg |
Absolute Pressure Fundamentals
Absolute pressure provides the complete pressure picture. It includes both the applied pressure and the atmospheric pressure surrounding the system.
The fundamental relationship is:
PSIA = PSIG + Atmospheric Pressure
At standard sea level conditions:
PSIA = PSIG + 14.7
Gauge Pressure Limitations
Gauge pressure measurements ignore atmospheric pressure variations. This creates problems when atmospheric pressure changes due to altitude or weather conditions.
Gauge pressure works well for most industrial applications because atmospheric pressure remains relatively constant at fixed locations. However, absolute pressure becomes critical for:
- Altitude compensation calculations
- Vacuum system design
- Gas law applications
- Flow rate calculations
- Temperature compensation
Practical Measurement Differences
I recently worked with Anna, a process engineer from a Norwegian offshore platform. Her pneumatic calculations worked perfectly onshore but failed when equipment moved to sea-based operations.
The issue was atmospheric pressure variation. Weather systems created 1-2 PSI atmospheric pressure changes that affected her gauge pressure readings. By switching to absolute pressure measurements, we eliminated weather-related performance variations.
Visual Understanding
Think of absolute pressure as measuring from the bottom of a swimming pool (perfect vacuum) to the water surface (system pressure). Gauge pressure measures only from the normal water level (atmospheric pressure) to the surface.
This analogy helps understand why absolute pressure provides more complete information for engineering calculations.
Why is Absolute Pressure Critical for Pneumatic Calculations?
Absolute pressure forms the foundation for accurate pneumatic system calculations. Many engineering formulas require absolute pressure values to produce correct results.
Absolute pressure is essential for pneumatic calculations because gas laws, flow equations, and thermodynamic relationships use absolute pressure values. Using gauge pressure in these formulas produces incorrect results that can lead to system failures.
Gas Law Applications
The ideal gas law2 requires absolute pressure for accurate calculations:
PV = nRT
Where:
- P = Absolute pressure
- V = Volume
- n = Number of moles
- R = Gas constant
- T = Absolute temperature3
Using gauge pressure in gas law calculations produces errors proportional to atmospheric pressure. At sea level, this creates 15% error in most calculations.
Flow Rate Calculations
Pneumatic flow rate formulas require absolute pressure ratios:
Flow Rate ∝ √(P₁² – P₂²)
Where P₁ and P₂ are absolute pressures upstream and downstream of a restriction.
Using gauge pressures in flow calculations can produce errors exceeding 20%, leading to undersized or oversized system components.
Cylinder Force Calculations
While basic force calculations (F = P × A) work with gauge pressure, advanced applications require absolute pressure:
Altitude Compensation
Force output changes with altitude due to atmospheric pressure variations. Absolute pressure calculations account for these changes.
Temperature Effects
Gas expansion and contraction calculations require absolute pressure and temperature values for accuracy.
Compressor Performance
Compressor sizing and performance calculations use absolute pressure ratios:
Compression Ratio = P₂(abs) ÷ P₁(abs)
This ratio determines compressor stage requirements and energy consumption. Using gauge pressures produces incorrect compression ratios4.
Real-World Example
I helped Marcus, a maintenance supervisor from a Swiss precision manufacturing facility, solve inconsistent rodless cylinder performance. His facility operated at 3,000 feet elevation, where atmospheric pressure is 13.2 PSI instead of sea level’s 14.7 PSI.
His gauge pressure readings showed 80 PSIG, but absolute pressure was only 93.2 PSIA instead of the expected 94.7 PSIA. This 1.5 PSI difference reduced cylinder force output by 1.6%, causing positioning accuracy problems in precision applications.
By recalibrating his calculations for local atmospheric pressure, we restored proper system performance.
Vacuum Applications
Vacuum systems require absolute pressure measurements because gauge pressure becomes negative below atmospheric pressure:
| Vacuum Level | Gauge Pressure | Absolute Pressure |
|---|---|---|
| Rough Vacuum | -10 PSIG | 4.7 PSIA |
| Medium Vacuum | -13 PSIG | 1.7 PSIA |
| High Vacuum | -14.5 PSIG | 0.2 PSIA |
| Perfect Vacuum | -14.7 PSIG | 0.0 PSIA |
How Does Altitude Affect Absolute Pressure in Pneumatic Systems?
Altitude significantly impacts atmospheric pressure, affecting pneumatic system performance. Understanding these effects prevents performance issues in elevated installations.
Atmospheric pressure decreases approximately 0.5 PSI per 1,000 feet of elevation gain. This reduction affects absolute pressure calculations and can reduce pneumatic cylinder force output by 3-4% per 1,000 feet of altitude.
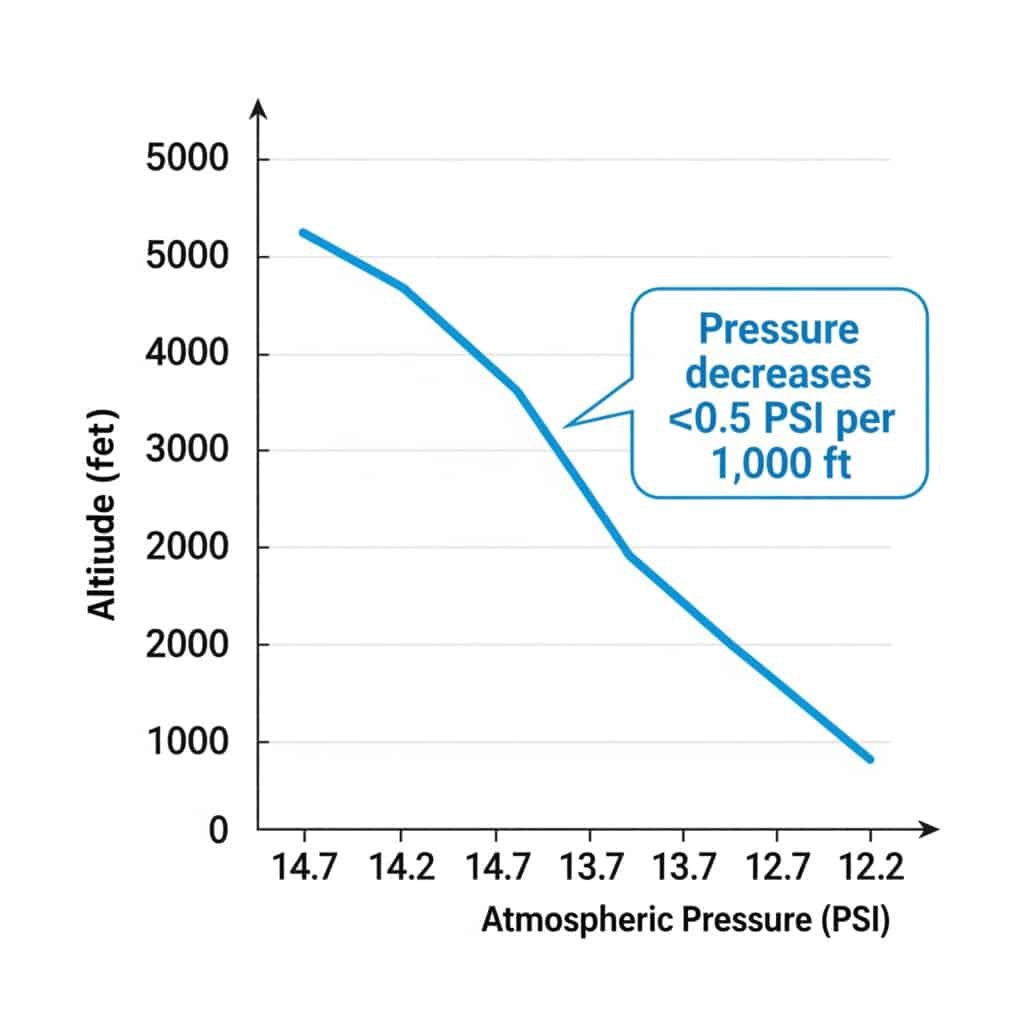
Atmospheric Pressure vs. Altitude
Standard atmospheric pressure varies predictably with altitude:
| Altitude (feet) | Atmospheric Pressure (PSIA) | Pressure Reduction |
|---|---|---|
| Sea Level | 14.7 | 0% |
| 1,000 | 14.2 | 3.4% |
| 2,000 | 13.7 | 6.8% |
| 5,000 | 12.2 | 17.0% |
| 10,000 | 10.1 | 31.3% |
Force Output Impact
Reduced atmospheric pressure affects cylinder force calculations when using absolute pressure:
Effective Pressure = Gauge Pressure + Local Atmospheric Pressure
For a cylinder operating at 80 PSIG:
- Sea Level: 80 + 14.7 = 94.7 PSIA
- 5,000 feet: 80 + 12.2 = 92.2 PSIA
- Force Reduction: 2.6%
Altitude Compensation Strategies
Several methods compensate for altitude effects:
Pressure Adjustment
Increase gauge pressure to maintain constant absolute pressure:
Required Gauge Pressure = Target Absolute Pressure – Local Atmospheric Pressure
System Redesign
Resize cylinders to maintain force output at reduced absolute pressure conditions.
Control System Compensation
Program control systems to adjust for local atmospheric pressure variations.
Temperature and Altitude Combined Effects
Both altitude and temperature affect air density and system performance:
Air Density = (Absolute Pressure × Molecular Weight) ÷ (Gas Constant × Absolute Temperature)
Higher altitudes typically have lower temperatures, partially offsetting pressure reduction effects on air density.
Real-World Altitude Application
I worked with Carlos, a project manager installing pneumatic systems at a mining operation in Peru at 12,000 feet elevation. His sea-level calculations showed adequate force for material handling applications.
At installation altitude, atmospheric pressure was only 9.3 PSIA compared to sea level’s 14.7 PSIA. This 37% reduction in atmospheric pressure significantly affected system performance.
We compensated by:
- Increasing operating pressure from 80 to 95 PSIG
- Upsizing critical cylinders by 15%
- Adding pressure boosters for high-force applications
The modified system delivered required performance despite extreme altitude conditions.
Weather Effects at Altitude
High-altitude locations experience greater atmospheric pressure variations due to weather:
Sea Level Variations
- High Pressure: 15.2 PSIA (+0.5 PSI)
- Low Pressure: 14.2 PSIA (-0.5 PSI)
- Total Range: 1.0 PSI
High Altitude Variations (10,000 feet)
- High Pressure: 10.6 PSIA (+0.5 PSI)
- Low Pressure: 9.6 PSIA (-0.5 PSI)
- Total Range: 1.0 PSI (10% of base pressure)
What Are the Common Applications of Absolute Pressure in Industrial Settings?
Absolute pressure measurements are essential in numerous industrial applications where accurate pressure relationships determine system performance and safety.
Common absolute pressure applications include vacuum systems, gas flow calculations, compressor sizing, altitude compensation, and thermodynamic processes. These applications require absolute pressure because gauge pressure measurements provide incomplete information.
Vacuum System Design
Vacuum applications require absolute pressure measurements because gauge pressure becomes negative below atmospheric conditions:
Vacuum Pump Sizing
Vacuum pump capacity depends on absolute pressure ratios:
Pumping Speed = Volume Flow Rate ÷ (P₁ – P₂)
Where P₁ and P₂ are absolute pressures at pump inlet and outlet.
Vacuum Level Specifications
Industrial vacuum levels use absolute pressure measurements:
| Application | Vacuum Level (PSIA) | Typical Use |
|---|---|---|
| Material Handling | 10-12 | Suction cups, conveyors |
| Packaging | 5-8 | Vacuum packaging |
| Process Industries | 1-3 | Distillation, drying |
| Laboratory | 0.1-0.5 | Research applications |
Gas Flow Measurement
Accurate gas flow calculations require absolute pressure values:
Choked Flow Conditions
Gas flow becomes choked when downstream pressure drops below critical pressure:
Critical Pressure Ratio = 0.528 (for air)
This calculation requires absolute pressures to determine flow limitations.
Mass Flow Calculations
Mass flow rate depends on absolute pressure and temperature:
Mass Flow = (Absolute Pressure × Area × Velocity) ÷ (Gas Constant × Absolute Temperature)
Compressor Applications
Compressor sizing and performance use absolute pressure ratios:
Compression Ratio Calculations
Compression Ratio = Discharge Pressure (abs) ÷ Suction Pressure (abs)
This ratio determines:
- Number of compression stages required
- Power consumption
- Discharge temperature
- Efficiency characteristics
Compressor Performance Maps
Manufacturer performance maps use absolute pressure conditions for accurate selection and operation.
Process Control Applications
Many process control systems require absolute pressure measurements:
Density Calculations
Gas density calculations for flow measurement and control:
Density = (Absolute Pressure × Molecular Weight) ÷ (Gas Constant × Absolute Temperature)
Heat Transfer Calculations
Thermodynamic calculations for heat exchangers and process equipment use absolute pressure and temperature values.
Real-World Process Application
I recently assisted Elena, a process engineer at a German chemical facility, with pneumatic conveying5 system design. Her system transported plastic pellets using compressed air through elevated pipelines.
The conveying calculations required absolute pressure values to determine:
- Air density at various pipeline elevations
- Pressure drop calculations through vertical sections
- Material velocity requirements
- System capacity limitations
Using gauge pressure would have produced 15-20% errors in conveying capacity calculations, leading to undersized equipment and poor performance.
Quality Control Applications
Precision manufacturing often requires absolute pressure measurements:
Leak Testing
Absolute pressure measurements provide more accurate leak detection:
Leak Rate = Volume × Pressure Drop ÷ Time
Using absolute pressure eliminates atmospheric pressure variations that affect gauge pressure readings.
Calibration Standards
Pressure calibration standards use absolute pressure references for accuracy and traceability.
How Do You Convert Between Different Pressure Measurements?
Pressure conversion between different measurement systems requires understanding reference points and conversion factors. Accurate conversions prevent calculation errors in international projects.
Pressure conversions require adding or subtracting atmospheric pressure when changing between absolute and gauge measurements, plus applying unit conversion factors. Common conversions include PSIA to bar, PSIG to kPa, and vacuum measurements to absolute pressure.
Basic Conversion Formulas
The fundamental relationship between pressure types:
Absolute Pressure = Gauge Pressure + Atmospheric Pressure
Gauge Pressure = Absolute Pressure – Atmospheric Pressure
Vacuum = Atmospheric Pressure – Absolute Pressure
Unit Conversion Factors
Common pressure unit conversions:
| From | To | Multiply By |
|——|—-|———–|
| PSI | bar | 0.06895 |
| bar | PSI | 14.504 |
| PSI | kPa | 6.895 |
| kPa | PSI | 0.1450 |
| PSI | “Hg | 2.036 |
| “Hg | PSI | 0.4912 |
Atmospheric Pressure Standards
Standard atmospheric pressure values for conversions:
| Location/Standard | Pressure Value |
|---|---|
| Sea Level Standard | 14.696 PSIA, 1.01325 bar |
| Engineering Standard | 14.7 PSIA, 1.013 bar |
| Metric Standard | 101.325 kPa, 760 mmHg |
Conversion Examples
PSIG to PSIA Conversion
80 PSIG to PSIA at sea level:
80 PSIG + 14.7 = 94.7 PSIA
Bar Gauge to Bar Absolute
5 barg to bara at sea level:
5 barg + 1.013 = 6.013 bara
Vacuum to Absolute Pressure
25 “Hg vacuum to PSIA:
14.7 – (25 × 0.4912) = 2.42 PSIA
International Unit Considerations
Different countries use various pressure units:
| Region | Common Units | Standard Atmospheric |
|---|---|---|
| USA | PSIG, PSIA | 14.7 PSI |
| Europe | bar, kPa | 1.013 bar |
| Asia | MPa, kgf/cm² | 1.033 kgf/cm² |
| Scientific | Pa, kPa | 101.325 kPa |
Conversion Accuracy Considerations
Conversion accuracy depends on atmospheric pressure assumptions:
Standard vs. Actual Conditions
- Standard: Uses 14.7 PSI atmospheric pressure
- Actual: Uses local atmospheric pressure
- Error: Can be 1-3% depending on location and weather
Temperature Effects
Atmospheric pressure varies with temperature and weather conditions. For precise conversions, use actual local atmospheric pressure rather than standard values.
Digital Conversion Tools
Modern pressure instruments often provide automatic unit conversions. However, understanding manual conversion principles helps verify digital readings and troubleshoot conversion errors.
Practical Conversion Application
I worked with Jean-Pierre, a project engineer from a French automotive supplier, on pneumatic system specifications for a global project. His European specifications used bar gauge pressure, but the North American installation required PSIG values.
The conversion process involved:
- European Spec: 6 barg operating pressure
- Convert to Absolute: 6 + 1.013 = 7.013 bara
- Convert Units: 7.013 × 14.504 = 101.7 PSIA
- Convert to Gauge: 101.7 – 14.7 = 87.0 PSIG
This systematic approach ensured accurate pressure specifications across different measurement systems and prevented equipment sizing errors.
What Mistakes Do Engineers Make with Absolute Pressure Calculations?
Absolute pressure calculation errors are common and can lead to significant system performance problems. Understanding these mistakes helps prevent costly design and operational issues.
Common absolute pressure mistakes include using gauge pressure in gas law calculations, ignoring atmospheric pressure variations, incorrect unit conversions, and misunderstanding vacuum measurements. These errors typically cause 10-30% calculation inaccuracies and system performance problems.
Using Gauge Pressure in Gas Law Calculations
The most common mistake is using gauge pressure in formulas that require absolute pressure:
Incorrect Gas Law Application
Wrong: PV = nRT using gauge pressure
Correct: PV = nRT using absolute pressure
This error creates calculation errors proportional to atmospheric pressure – approximately 15% at sea level conditions.
Ignoring Atmospheric Pressure Variations
Many engineers assume constant 14.7 PSI atmospheric pressure regardless of location or conditions:
Location Variations
- Sea Level: 14.7 PSIA
- Denver (5,280 ft): 12.2 PSIA
- Error: 17% if using sea level value in Denver
Weather Variations
- High Pressure System: 15.2 PSIA
- Low Pressure System: 14.2 PSIA
- Variation: ±3.4% from standard
Incorrect Unit Conversions
Mixing absolute and gauge pressure units creates significant errors:
Common Conversion Mistakes
- Adding 14.7 to bar gauge readings (should add 1.013)
- Using 14.7 PSI for non-sea-level locations
- Forgetting to convert between absolute and gauge when changing units
Vacuum Measurement Confusion
Vacuum measurements often confuse engineers because they represent pressure below atmospheric:
Vacuum Pressure Relationships
- 29 “Hg Vacuum = 0.76 PSIA (not -29 PSIA)
- Perfect Vacuum = 0 PSIA absolute
- Atmospheric Pressure = Maximum possible vacuum in “Hg
I recently helped Roberto, a design engineer from an Italian packaging company, resolve vacuum system performance issues. His calculations showed adequate vacuum pump capacity, but the system couldn’t achieve required vacuum levels.
The problem was vacuum measurement confusion. Roberto calculated pump requirements using -25 PSIG instead of the correct 1.4 PSIA absolute pressure. This error made the pump appear 18 times more powerful than actual capacity.
Temperature Compensation Errors
Absolute pressure calculations often ignore temperature effects:
Gas Law Temperature Requirements
Gas law calculations require absolute temperature (Rankine or Kelvin):
- Fahrenheit to Rankine: °R = °F + 459.67
- Celsius to Kelvin: K = °C + 273.15
Using Fahrenheit or Celsius temperatures in gas law calculations produces significant errors.
Altitude Compensation Oversights
Engineers frequently use sea-level atmospheric pressure for high-altitude installations:
Altitude Pressure Errors
At 10,000 feet elevation:
- Actual Atmospheric: 10.1 PSIA
- Sea Level Assumption: 14.7 PSIA
- Error: 45% overestimate of absolute pressure
Compressor Ratio Calculation Mistakes
Compression ratio calculations require absolute pressures, but engineers often use gauge pressures:
Incorrect Compression Ratio
For 80 PSIG discharge, atmospheric suction:
- Wrong: 80 ÷ 0 = undefined
- Correct: 94.7 ÷ 14.7 = 6.44:1
Flow Calculation Errors
Flow rate calculations using pressure differentials require absolute pressure values:
Choked Flow Mistakes
Critical pressure ratio calculations:
- Wrong: Using gauge pressure ratios
- Correct: Using absolute pressure ratios
- Impact: Can overestimate flow capacity by 15-20%
Safety System Design Errors
Safety relief valve sizing requires absolute pressure calculations:
Relief Valve Sizing
Relief valve capacity depends on absolute pressure ratios. Using gauge pressures can result in undersized relief valves and safety hazards.
Prevention Strategies
Avoid absolute pressure calculation mistakes through:
Systematic Approach
- Identify Required Pressure Type: Determine if calculation needs absolute or gauge pressure
- Use Correct Atmospheric Pressure: Apply local atmospheric pressure, not standard sea level
- Verify Unit Consistency: Ensure all pressures use same unit system
- Double-Check Conversions: Verify conversion factors and reference points
Documentation Standards
- Clearly Label Pressure Types: Always specify PSIA, PSIG, bara, barg
- State Reference Conditions: Document atmospheric pressure assumptions
- Include Conversion Tables: Provide reference conversion factors
Conclusion
Absolute pressure provides the complete pressure picture essential for accurate pneumatic system calculations. Understanding absolute pressure principles prevents common calculation errors and ensures reliable rodless cylinder system performance across varying operating conditions.
FAQs About Absolute Pressure in Pneumatic Systems
What is the difference between absolute pressure and gauge pressure?
Absolute pressure measures total pressure from perfect vacuum, while gauge pressure measures pressure above atmospheric. Absolute pressure equals gauge pressure plus atmospheric pressure (14.7 PSI at sea level).
Why do pneumatic calculations require absolute pressure?
Gas laws, flow equations, and thermodynamic calculations require absolute pressure because they involve pressure ratios and relationships that need complete pressure values. Using gauge pressure produces calculation errors of 10-30%.
How does altitude affect absolute pressure in pneumatic systems?
Atmospheric pressure decreases about 0.5 PSI per 1,000 feet of elevation. This reduces absolute pressure and can decrease cylinder force output by 3-4% per 1,000 feet unless compensated through pressure adjustments.
How do you convert gauge pressure to absolute pressure?
Add atmospheric pressure to gauge pressure: PSIA = PSIG + atmospheric pressure. Use local atmospheric pressure (varies with altitude) rather than standard 14.7 PSI for accurate conversions.
What happens if you use gauge pressure in absolute pressure calculations?
Using gauge pressure in formulas requiring absolute pressure creates errors proportional to atmospheric pressure – typically 15% at sea level. These errors can cause undersized equipment and poor system performance.
Do rodless cylinders require absolute pressure calculations?
Yes, rodless cylinders use the same pressure relationships as traditional cylinders. Force calculations, flow sizing, and performance analysis all benefit from absolute pressure values, especially in altitude or vacuum applications.
-
Learn about the design and operational advantages of rodless pneumatic cylinders, which are often used in material handling and automation. ↩
-
Explore the Ideal Gas Law (PV=nRT), a fundamental equation of state that describes the relationship between pressure, volume, and temperature of a gas. ↩
-
Learn about absolute temperature scales like Kelvin and Rankine and why they are essential for thermodynamic and gas law calculations. ↩
-
Understand the importance of the compression ratio in compressor performance and how it is calculated using absolute pressures. ↩
-
Discover how pneumatic conveying systems work to transport bulk materials using compressed gas in industrial processes. ↩




