Die Physik, die hinter Drehantrieben mit Flügeln steckt, umfasst komplexe Wechselwirkungen zwischen Fluiddynamik, mechanischen Kräften und Thermodynamik, die die meisten Ingenieure nie ganz verstehen. Die Beherrschung dieser Prinzipien ist jedoch entscheidend für die Optimierung der Leistung, die Vorhersage des Verhaltens und die Lösung von Anwendungsproblemen, die über Erfolg oder Misserfolg eines Projekts entscheiden können. 🔬
Drehantriebe mit Flügeln arbeiten nach dem Pascal'schen Prinzip der Druckmultiplikation und wandeln eine lineare pneumatische Kraft durch gleitende Flügelmechanismen in ein Rotationsdrehmoment um, wobei die Leistung durch Druckunterschiede, Flügelgeometrie, Reibungskoeffizienten und thermodynamische Gasgesetze bestimmt wird, die die Drehmomentabgabe, die Geschwindigkeit und die Wirkungsgradmerkmale bestimmen.
Kürzlich arbeitete ich mit einer Konstrukteurin namens Jennifer in einem Luft- und Raumfahrtbetrieb in Seattle zusammen, die mit Drehmomentinkonsistenzen in ihrer Drehantriebsanwendung zu kämpfen hatte. Ihre Stellantriebe erzeugten 30% weniger Drehmoment als berechnet, was zu Positionierungsfehlern bei kritischen Montagevorgängen führte. Die Ursache war nicht mechanisch, sondern ein grundlegendes Missverständnis der physikalischen Zusammenhänge, die das Verhalten von Lamellenantrieben bestimmen. ✈️
Inhaltsübersicht
- Wie erzeugt die Druckdynamik ein Drehmoment in Flügelradaktoren?
- Welche Rolle spielt die Schaufelgeometrie bei der Bestimmung der Leistungsmerkmale von Aktuatoren?
- Welche thermodynamischen Prinzipien beeinflussen die Geschwindigkeit und den Wirkungsgrad von Drehantrieben?
- Wie wirken sich Reibungskräfte und mechanische Verluste auf die Leistung von Aktuatoren in der Praxis aus?
Wie erzeugt die Druckdynamik ein Drehmoment in Flügelradaktoren?
Das Verständnis der Druck-Drehmoment-Umwandlung ist für die Konstruktion und Anwendung von Drehantrieben von grundlegender Bedeutung.
Lamellenantriebe erzeugen ein Drehmoment durch Druckunterschiede, die auf die Lamellenoberflächen wirken, wobei das Drehmoment gleich der Druckdifferenz mal der effektiven Lamellenfläche mal Hebelarm1 Abstand, mit der Beziehung T = ΔP × A × r, modifiziert durch Schaufelwinkel und Kammergeometrie, um aus linearen pneumatischen Kräften eine Drehbewegung zu erzeugen.
Grundlegende Prinzipien der Drehmomenterzeugung
Das Pascalsche Prinzip Anwendung
Die Grundlage für den Betrieb von Drehantrieben liegt in Pascalsches Prinzip2:
- Druckübertragung: Gleichmäßiger Druck wirkt auf alle Oberflächen innerhalb der Kammer
- Kraftmultiplikation: Druck × Fläche = Kraft auf jede Schaufelfläche
- Schaffung von Momenten: Kraft × Radius = Drehmoment um die Mittelachse
Grundlagen der Drehmomentberechnung
Grundlegende Formel für das Drehmoment: T = ΔP × A_eff × r_eff × η
Wo:
- T = Abtriebsdrehmoment (lb-in)
- ΔP = Druckdifferenz (PSI)
- A_eff = Effektive Schaufelfläche (sq in)
- r_eff = Effektiver Momentarm (Zoll)
- η = Mechanischer Wirkungsgrad (0,85-0,95)
Analyse der Druckverteilung
Dynamik des Kammerdrucks
Die Druckverteilung in den Schaufelkammern ist nicht gleichmäßig:
- Hochdruckkammer: Versorgungsdruck minus Strömungsverluste
- Niederdruckkammer: Abgasdruck plus Gegendruck
- Übergangszonen: Druckgradienten an den Schaufelkanten
- Tote Bände: Lufteinschlüsse in Zwischenräumen
Berechnungen der effektiven Fläche
| Schaufel-Konfiguration | Formel für die wirksame Fläche | Wirkungsgrad-Faktor |
|---|---|---|
| Einzelne Schaufel | A = L × W × sin(θ) | 0.85-0.90 |
| Doppelfahne | A = 2 × L × W × sin(θ/2) | 0.88-0.93 |
| Mehrflügelig | A = n × L × W × sin(θ/n) | 0.90-0.95 |
wobei L = Schaufellänge, W = Schaufelbreite, θ = Drehwinkel, n = Anzahl der Schaufeln
Dynamische Druckeffekte
Durchflussinduzierte Druckverluste
Die Druckdynamik in der realen Welt beinhaltet auch strömungsbedingte Verluste:
- Einlassbeschränkungen: Druckabfall bei Ventilen und Armaturen
- Interne Strömungsverluste: Turbulenz und Reibung in Kammern
- Auspuff-Beschränkungen: Gegendruck aus Abgasanlagen
- Beschleunigungsverluste: Druck, der erforderlich ist, um bewegte Luft zu beschleunigen
Jennifers Luft- und Raumfahrtanwendung litt unter einer unzureichenden Dimensionierung der Versorgungsleitung, die bei schnellen Bewegungen des Aktuators einen Druckabfall von 15 PSI verursachte. Dieser Druckverlust in Verbindung mit dynamischen Strömungseffekten erklärte den Drehmomentabfall von 30%, den sie feststellte. 📉
Welche Rolle spielt die Schaufelgeometrie bei der Bestimmung der Leistungsmerkmale von Aktuatoren?
Die Schaufelgeometrie hat einen direkten Einfluss auf Drehmoment, Drehwinkel, Geschwindigkeit und Wirkungsgrad.
Die Flügelgeometrie bestimmt die Leistung des Aktuators durch die Länge der Flügel (beeinflusst die Drehmomentstütze), die Breite (bestimmt den Druckbereich), die Dicke (beeinflusst die Abdichtung und die Reibung), die Winkelverhältnisse (steuert den Drehbereich) und die Spaltspezifikationen (beeinflusst die Leckage und den Wirkungsgrad), wobei jeder Parameter für bestimmte Anwendungen optimiert werden muss.
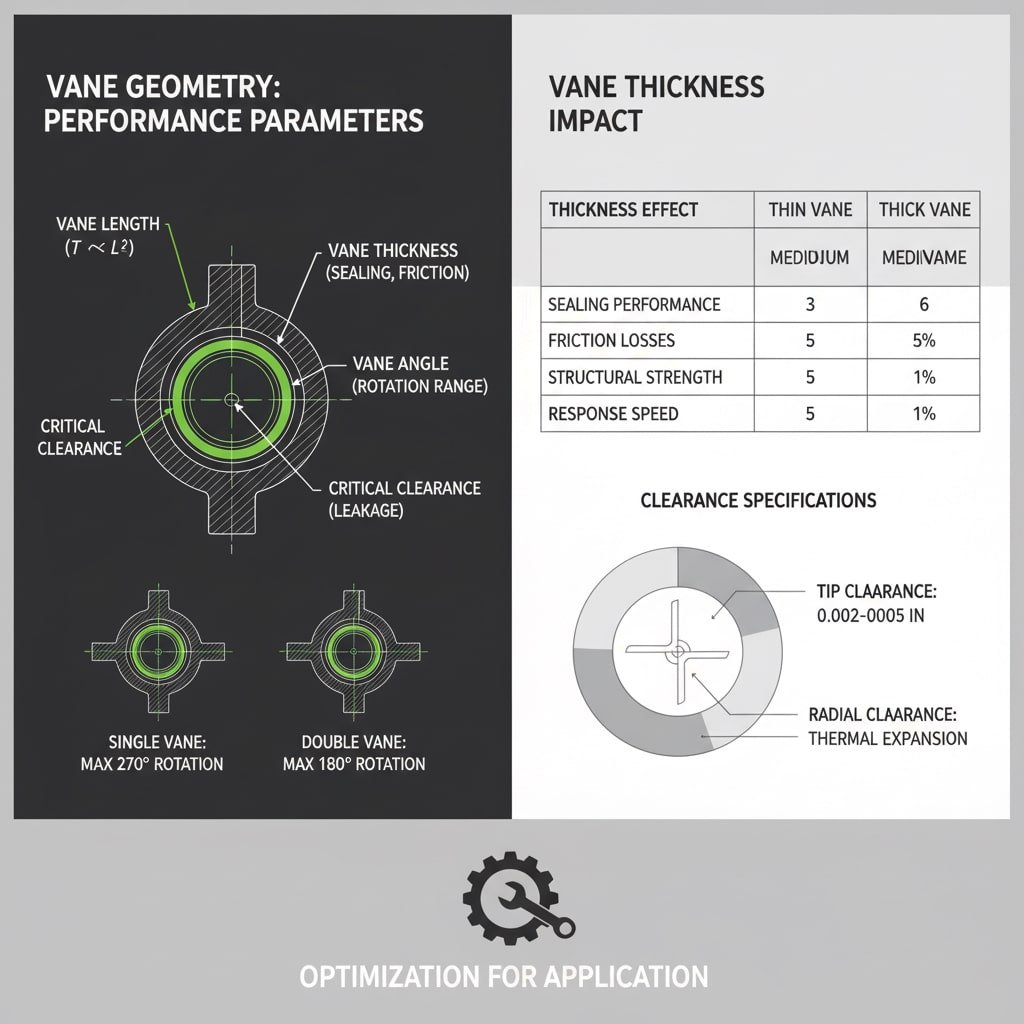
Geometrische Parameteranalyse
Optimierung der Schaufellänge
Die Schaufellänge wirkt sich direkt auf die Drehmomentabgabe und die strukturelle Integrität aus:
- Verhältnis der Drehmomente: T ∝ L² (Verhältnis der Länge zum Quadrat)
- Überlegungen zu Stress: Die Biegespannung steigt mit der Länge im Kubus
- Ablenkungseffekte: Längere Schaufeln erfahren eine stärkere Auslenkung der Spitze
- Optimale Verhältnisse: Längen-Breiten-Verhältnisse von 3:1 bis 5:1 bieten die beste Leistung
Lamellendicke Auswirkung
Die Lamellendicke beeinflusst mehrere Leistungsparameter:
| Dicken-Effekt | Dünne Schaufeln (< 0,25″) | Mittlere Schaufeln (0,25″-0,5″) | Dicke Schaufeln (> 0,5″) |
|---|---|---|---|
| Versiegelungsleistung | Schlecht - hohe Leckage | Gut - angemessener Kontakt | Ausgezeichnet - dichte Dichtungen |
| Reibungsverluste | Niedrig | Mittel | Hoch |
| Strukturelle Stärke | Schlecht - Ablenkungsprobleme | Gut - ausreichende Steifigkeit | Ausgezeichnet - starr |
| Reaktionsgeschwindigkeit | Schnell | Mittel | Langsam |
Überlegungen zur Winkelgeometrie
Beschränkungen des Rotationswinkels
Die Geometrie der Schaufeln begrenzt die maximalen Drehwinkel:
- Einzelne Schaufel: Maximum ~270° Drehung
- Doppelte Windfahne: Maximal ~180° Drehung
- Mehrflügelig: Begrenzung der Drehung durch Überlagerung der Schaufeln
- Konstruktion der Kammer: Die Gehäusegeometrie beeinflusst den nutzbaren Winkel
Optimierung des Schaufelwinkels
Der Winkel zwischen den Schaufeln beeinflusst das Drehmomentverhalten:
- Gleiche Abstände: Sorgt für eine gleichmäßige Drehmomentabgabe
- Ungleiche Abstände: Kann Drehmomentkurven für bestimmte Anwendungen optimieren
- Progressive Blickwinkel: Kompensieren Sie Druckschwankungen
Freiraum und Dichtungsgeometrien
Spezifikationen für kritische Freiräume
Ein angemessenes Spiel sorgt für ein Gleichgewicht zwischen Dichtungswirkung und Reibung:
- Tipp-Abstand: 0,002″-0,005″ für optimale Abdichtung
- Seitlicher Abstand: 0,001″-0,003″ zur Vermeidung von Bindungen
- Radiales Spiel: Überlegungen zur Temperaturausdehnung
- Axiales Spiel: Axiallager und thermisches Wachstum
Bei Bepto verwendet unser Prozess zur Optimierung der Schaufelgeometrie numerische Strömungsmechanik (CFD)3 Analyse in Kombination mit empirischen Tests, um die ideale Balance zwischen Drehmoment, Geschwindigkeit und Effizienz für jede Anwendung zu erreichen. Dieser technische Ansatz hat es uns ermöglicht, einen 15-20% höheren Wirkungsgrad als bei Standardkonstruktionen zu erzielen. 🔧
Welche thermodynamischen Prinzipien beeinflussen die Geschwindigkeit und den Wirkungsgrad von Drehantrieben?
Thermodynamische Effekte wirken sich erheblich auf die Leistung von Aktuatoren aus, insbesondere bei Anwendungen mit hohen Geschwindigkeiten oder hoher Belastung.
Zu den thermodynamischen Prinzipien, die sich auf Drehantriebe auswirken, gehören die Gasausdehnung und -kompression während der Rotation, die Wärmeerzeugung durch Reibung und Druckabfall, Temperatureffekte auf die Luftdichte und -viskosität sowie adiabatische bzw. isotherme Prozesse, die die tatsächliche gegenüber der theoretischen Leistung unter realen Betriebsbedingungen bestimmen.

Anwendungen des Gasgesetzes
Auswirkungen des idealen Gasgesetzes
Die Leistung von Drehantrieben folgt den Beziehungen des Gasgesetzes:
- Druck-Volumen-Arbeit: W = ∫P dV bei der Ausdehnung
- Auswirkungen der Temperatur: PV = nRT regelt die Druck-Temperatur-Beziehungen
- Schwankungen in der Dichte: ρ = PM/RT wirkt sich auf die Berechnung des Massendurchflusses aus.
- Komprimierbarkeit: Reale Gaseffekte bei hohen Drücken
Adiabatische vs. Isotherme Prozesse
Der Betrieb eines Stellantriebs umfasst beide Verfahrensarten:
| Prozess-Typ | Merkmale | Auswirkungen auf die Leistung |
|---|---|---|
| Adiabatisch | Keine Wärmeübertragung, schnelle Ausdehnung | Höhere Druckabfälle, Temperaturänderungen |
| Isotherme | Konstante Temperatur, langsame Ausdehnung | Effizientere Energieumwandlung |
| Polytropisch | Kombination in der realen Welt | Tatsächliche Leistung zwischen den Extremen |
Wärmeerzeugung und -übertragung
Reibungsinduzierte Erwärmung
In Drehantrieben gibt es mehrere Wärmequellen:
- Reibung der Schaufelspitze: Gleitender Kontakt mit dem Gehäuse
- Reibung der Lager: Lagerverluste der Wellenlagerung
- Reibung der Dichtung: Schleppkräfte der Gleitringdichtung
- Flüssigkeitsreibung: Viskose Verluste im Luftstrom
Berechnungen des Temperaturanstiegs
Wärmeerzeugungsrate: Q = μ × N × F × V
Wo:
- Q = Wärmeerzeugung (BTU/hr)
- μ = Reibungskoeffizient
- N = Rotationsgeschwindigkeit (RPM)
- F = Normalkraft (lbs)
- V = Gleitgeschwindigkeit (ft/min)
Analyse der Effizienz
Thermodynamische Wirkungsgrad-Faktoren
Die Gesamteffizienz kombiniert mehrere Verlustmechanismen:
- Volumetrischer Wirkungsgrad: ηv = Tatsächlicher Durchfluss / Theoretischer Durchfluss
- Mechanischer Wirkungsgrad: ηm = Ausgangsleistung / Eingangsleistung
- Allgemeine Effizienz: ηo = ηv × ηm
Strategien zur Optimierung der Effizienz
| Strategie | Effizienzgewinn | Durchführung Kosten |
|---|---|---|
| Verbesserte Abdichtung | 5-15% | Mittel |
| Optimierte Abstände | 3-8% | Niedrig |
| Fortschrittliche Materialien | 8-12% | Hoch |
| Thermisches Management | 5-10% | Mittel |
Strömungsdynamik und Druckverluste
Auswirkungen der Reynoldszahl
Die Fließeigenschaften ändern sich mit den Betriebsbedingungen:
- Laminare Strömung: Re < 2300, vorhersehbare Druckverluste
- Turbulente Strömung: Re > 4000, höhere Reibungsfaktoren
- Übergangsregion: Unvorhersehbare Fließeigenschaften
Die thermodynamische Analyse ergab, dass bei Jennifers Luft- und Raumfahrtanwendung während der schnellen Zyklen ein erheblicher Temperaturanstieg zu verzeichnen war, der die Luftdichte um 12% verringerte und zum Drehmomentverlust beitrug. Wir implementierten Wärmemanagementstrategien, die die volle Leistung wiederherstellten. 🌡️
Wie wirken sich Reibungskräfte und mechanische Verluste auf die Leistung von Aktuatoren in der Praxis aus?
Reibung und mechanische Verluste verringern die theoretische Leistung erheblich und müssen für einen optimalen Betrieb des Aktuators sorgfältig gesteuert werden.
Zu den mechanischen Verlusten in Lamellenantrieben gehören die Gleitreibung an den Lamellenspitzen, der Luftwiderstand der Rotationsdichtung, die Lagerreibung und interne Luftturbulenzen, die das theoretische Drehmoment in der Regel um 10-20% reduzieren und eine sorgfältige Materialauswahl, Oberflächenbehandlung und Schmierungsstrategien erfordern, um Leistungseinbußen zu minimieren.
Analyse und Modellierung der Reibung
Reibungsmechanismen für Schaufelspitzen
Die primäre Reibungsquelle tritt an den Schnittstellen zwischen Schaufel und Gehäuse auf:
- Schmierung an der Grenze: Direkter Metall-auf-Metall-Kontakt
- Gemischte Schmierung: Partielle Flüssigkeitsfilmabscheidung
- Hydrodynamische Schmierung: Vollständiger Flüssigkeitsfilm (selten in der Pneumatik)
Variationen des Reibungskoeffizienten
| Werkstoff-Kombination | Trockenreibung (μ) | Geschmierte Reibung (μ) | Temperatur-Empfindlichkeit |
|---|---|---|---|
| Stahl auf Stahl | 0.6-0.8 | 0.1-0.15 | Hoch |
| Stahl auf Bronze | 0.3-0.5 | 0.08-0.12 | Mittel |
| Stahl auf PTFE | 0.1-0.2 | 0.05-0.08 | Niedrig |
| Keramische Beschichtung | 0.2-0.3 | 0.06-0.10 | Sehr niedrig |
Analyse der Lagerverluste
Reibung von Radiallagern
Die Lager der Abtriebswelle verursachen erhebliche Verluste:
- Rollende Reibung: Fr = μr × N × r
- Gleitende Reibung: Fs = μs × N
- Viskose Reibung: Fv = η × A × V/h
- Reibung der Dichtung: Zusätzlicher Widerstand durch Wellendichtungen
Auswirkungen der Lagerauswahl
Unterschiedliche Lagertypen beeinflussen den Gesamtwirkungsgrad:
- Kugellager: Geringe Reibung, hohe Präzision
- Rollenlager: Höhere Belastbarkeit, mäßige Reibung
- Gleitlager: Hohe Reibung, einfache Konstruktion
- Magnetische Lager: Nahezu keine Reibung, hohe Kosten
Lösungen für die Oberflächentechnik
Fortgeschrittene Oberflächenbehandlungen
Moderne Oberflächenbehandlungen verringern die Reibung drastisch:
- Hartverchromung: Verringert den Verschleiß, mäßige Reibungsreduzierung
- Keramische Beschichtungen: Ausgezeichnete Verschleißfestigkeit, geringe Reibung
- Diamantähnlicher Kohlenstoff (DLC): Ultra-niedrige Reibung, teuer
- Spezialisierte Polymere: Anwendungsspezifische Lösungen
Strategien für die Schmierung
| Schmierung Methode | Reibungsreduzierung | Anforderungen an die Wartung | Auswirkungen auf die Kosten |
|---|---|---|---|
| Ölnebel-Systeme | 60-80% | Hoch - regelmäßiger Nachschub | Hoch |
| Festschmierstoffe | 40-60% | Niedrig - lange Lebensdauer | Mittel |
| Selbstschmierende Materialien | 50-70% | Sehr niedrig - dauerhaft | Hohe anfängliche |
| Trockenfilm-Schmierstoffe | 30-50% | Mittel - regelmäßige Wiederaufbringung | Niedrig |
Strategien zur Leistungsoptimierung
Integrierter Design-Ansatz
Bei Bepto optimieren wir Reibung durch systematisches Design:
- Auswahl der Materialien: Kompatible Materialpaare
- Oberflächenbehandlung: Optimierte Rauhigkeit für jede Anwendung
- Freiraumkontrolle: Anpressdruck minimieren
- Wärmemanagement: Kontrolle der temperaturbedingten Ausdehnung
Validierung der Leistung in der realen Welt
Labortests und die Leistung in der Praxis weichen oft voneinander ab:
- Einlaufeffekte: Die Leistung verbessert sich mit der ersten Inbetriebnahme
- Auswirkungen der Kontamination: Realitätsnahe Schmutz- und Schutteffekte
- Temperaturwechsel: Thermische Ausdehnung und Kontraktion
- Lastschwankungen: Dynamische Belastung gegenüber statischen Prüfbedingungen
Dank unserer umfassenden Reibungsanalyse und unseres Optimierungsprogramms konnte Jennifer mit ihrer Luft- und Raumfahrtanwendung ein theoretisches Drehmoment von 95% erreichen - eine erhebliche Verbesserung gegenüber den ursprünglichen 70%. Der Schlüssel dazu war die Umsetzung eines vielschichtigen Ansatzes, der fortschrittliche Materialien, eine optimierte Geometrie und die richtige Schmierung kombiniert. 🎯
Prädiktive Reibungsmodellierung
Mathematische Reibungsmodelle
Eine genaue Reibungsvorhersage erfordert eine ausgeklügelte Modellierung:
- Coulombsche Reibung: F = μ × N (Grundmodell)
- Stribeck-Kurve: Veränderung der Reibung mit der Geschwindigkeit
- Auswirkungen der Temperatur: μ(T) Beziehungen
- Verlauf der Abnutzung: Reibung ändert sich mit der Zeit
Schlussfolgerung
Das Verständnis der grundlegenden physikalischen Zusammenhänge von Drehflügelantrieben - von der Druckdynamik über die Thermodynamik bis hin zu Reibungsmechanismen - ermöglicht es Ingenieuren, die Leistung zu optimieren, das Verhalten vorherzusagen und komplexe Anwendungsprobleme zu lösen.
Häufig gestellte Fragen zur Physik der Flügelzellen-Drehantriebe
F: Wie wirkt sich der Betriebsdruck auf das Verhältnis zwischen theoretischer und tatsächlicher Drehmomentabgabe aus?
A: Höhere Betriebsdrücke verbessern im Allgemeinen das Verhältnis von theoretischem zu tatsächlichem Drehmoment, da die mechanischen Verluste einen geringeren Prozentsatz der Gesamtleistung ausmachen. Allerdings erhöht ein höherer Druck auch die Reibungskräfte, so dass die Beziehung nicht linear ist. Der optimale Druck hängt von den spezifischen Anwendungsanforderungen und der Antriebskonstruktion ab.
F: Warum verlieren Drehantriebe bei hohen Drehzahlen an Drehmoment, und wie kann dies minimiert werden?
A: Drehmomentverluste bei hohen Drehzahlen sind auf erhöhte Reibung, Strömungsbeschränkungen und thermodynamische Effekte zurückzuführen. Minimieren Sie die Verluste durch eine optimierte Dimensionierung der Anschlüsse, moderne Lagersysteme, verbesserte Dichtungskonstruktionen und Wärmemanagement. Ab bestimmten Geschwindigkeiten wird die Strömungsgeschwindigkeit zur wichtigsten Einschränkung.
F: Wie wirken sich Temperaturschwankungen auf die Berechnung der Leistung von Drehantrieben aus?
A: Die Temperatur beeinflusst die Luftdichte (wirkt sich auf die Kraft aus), die Viskosität (beeinflusst den Durchfluss), die Materialeigenschaften (verändert die Reibung) und die Wärmeausdehnung (verändert das Spiel). Ein Temperaturanstieg um 100°F kann die Drehmomentleistung durch kombinierte Effekte um 15-25% verringern. Die Temperaturkompensation in Steuersystemen hilft, die Leistung konstant zu halten.
F: Welcher Zusammenhang besteht zwischen der Geschwindigkeit der Schaufelspitze und den Reibungsverlusten in Drehantrieben?
A: Die Reibungsverluste steigen im Allgemeinen mit dem Quadrat der Spitzengeschwindigkeit, da die Kontaktkräfte und die Wärmeentwicklung zunehmen. Bei sehr niedrigen Geschwindigkeiten dominiert jedoch die statische Reibung, was zu einer komplexen Beziehung führt. Optimale Betriebsgeschwindigkeiten liegen typischerweise im mittleren Bereich, wo die dynamische Reibung überschaubar ist.
F: Wie werden die Auswirkungen der Luftkompressibilität bei der Berechnung der Leistung von Drehantrieben berücksichtigt?
A: Die Kompressibilität der Luft wird bei Drücken über 100 PSI und bei schneller Beschleunigung bedeutsam. Verwenden Sie kompressible Strömungsgleichungen anstelle von inkompressiblen Annahmen, berücksichtigen Sie Verzögerungen bei der Druckwellenausbreitung und berücksichtigen Sie adiabatische Expansionseffekte. Für Hochdruckanwendungen über 200 PSI werden möglicherweise echte Gaseigenschaften benötigt.
-
Lernen Sie die Definition eines Hebelarms kennen, d. h. den senkrechten Abstand zwischen einer Drehachse und der Wirkungslinie einer Kraft, der für die Berechnung des Drehmoments entscheidend ist. ↩
-
Verstehen des Pascalschen Prinzips, des grundlegenden Gesetzes der Strömungsmechanik, das erklärt, wie Druck in einer eingeschlossenen Flüssigkeit übertragen wird. ↩
-
Erforschen Sie das Gebiet der numerischen Strömungsmechanik (Computational Fluid Dynamics, CFD), ein Teilgebiet der Strömungsmechanik, das numerische Analysen zur Lösung und Analyse von Problemen mit Flüssigkeitsströmungen einsetzt. ↩




