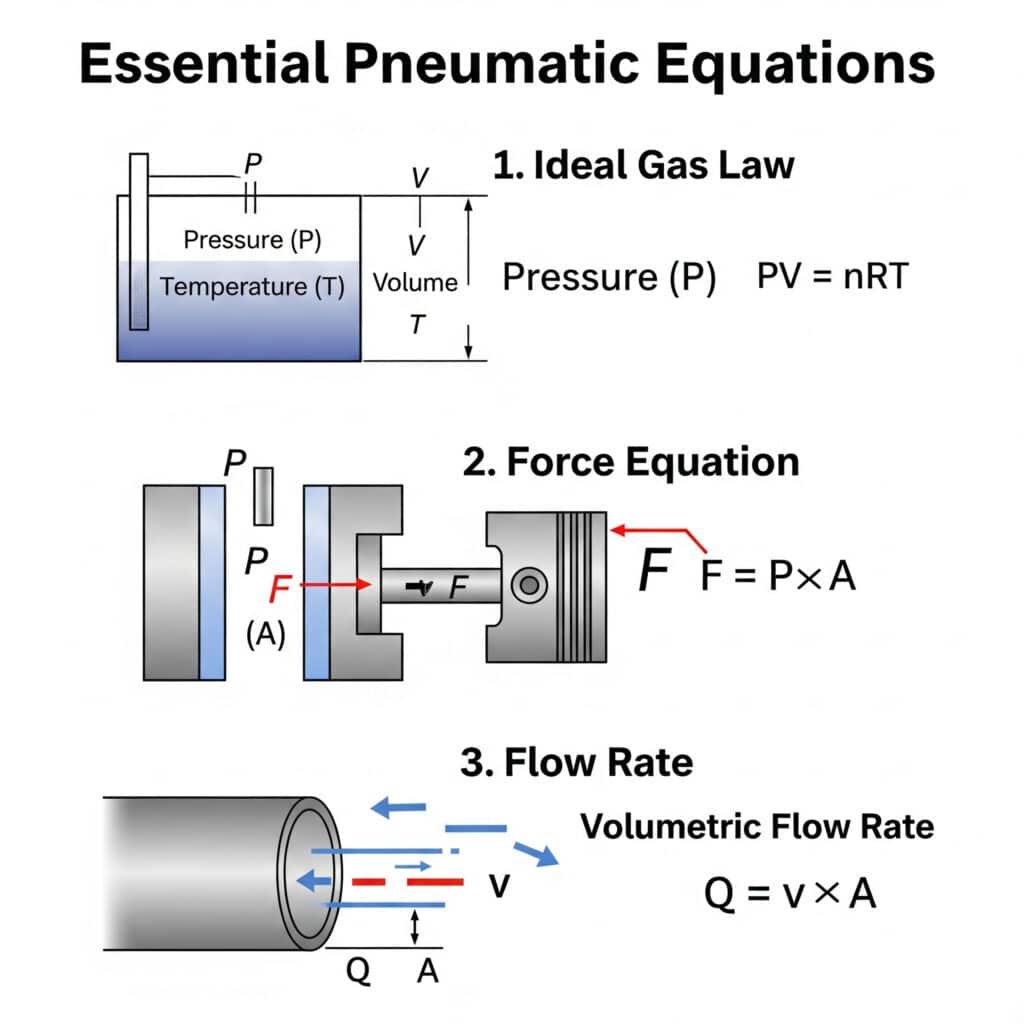
Êtes-vous constamment aux prises avec des calculs de systèmes pneumatiques ? De nombreux ingénieurs sont confrontés au même problème lorsqu'ils conçoivent ou dépannent des systèmes pneumatiques. La bonne nouvelle, c'est que la maîtrise de quelques équations clés peut résoudre la plupart de vos problèmes pneumatiques.
Les équations essentielles de la transmission pneumatique que tout ingénieur devrait connaître sont les suivantes loi des gaz idéaux (PV = nRT)1L'équation de la force (F = P × A) et la relation du débit (Q = v × A). La compréhension de ces principes fondamentaux permet de concevoir des systèmes et de les dépanner avec précision.
J'ai passé plus de 15 ans à travailler avec des systèmes pneumatiques chez Bepto, et j'ai vu de mes propres yeux comment la compréhension de ces équations de base peut permettre d'économiser des milliers d'euros en temps d'arrêt et d'éviter des erreurs de conception coûteuses.
Table des matières
- Dérivation de l'équation des gaz : Pourquoi PV = nRT est-il important dans les systèmes pneumatiques ?
- Quelle est la relation entre la force, la pression et la surface dans les cylindres pneumatiques ?
- Quelle est la relation entre le débit et la vitesse dans les systèmes pneumatiques ?
- Conclusion
- FAQ sur les équations de transmission pneumatique
Dérivation de l'équation des gaz : Pourquoi PV = nRT est-il important dans les systèmes pneumatiques ?
Lors de la conception de systèmes pneumatiques, il est essentiel de comprendre comment les gaz se comportent dans différentes conditions. Cette connaissance peut faire la différence entre un système qui fonctionne de manière fiable et un système qui tombe en panne de manière inattendue.
La loi des gaz idéaux (PV = nRT) est fondamentale pour les systèmes pneumatiques car elle décrit l'interaction entre la pression, le volume et la température. Cette relation aide les ingénieurs à prévoir le comportement de l'air dans les vérins sans tige et autres composants pneumatiques dans des conditions de fonctionnement variables.
La loi des gaz idéaux peut sembler être un concept théorique issu des cours de physique, mais elle a des applications pratiques directes dans les systèmes pneumatiques. Permettez-moi de l'expliquer en termes plus pratiques.
Comprendre les variables dans PV = nRT
| Variable | Signification | Application pneumatique |
|---|---|---|
| P | Pression | Pression de service dans votre système |
| V | Volume | Taille de la chambre à air en cylindres |
| n | Nombre de moles | Quantité d'air dans le système |
| R | Constante de gaz2 | Constante universelle (8,314 J/mol-K) |
| T | Température | Température de fonctionnement |
Comment la température affecte-t-elle les performances pneumatiques ?
Les variations de température peuvent avoir un impact significatif sur les performances des systèmes pneumatiques. L'année dernière, Hans, l'un de nos clients en Allemagne, m'a contacté au sujet de l'irrégularité des performances de son système de vérins sans tige. Le système fonctionnait parfaitement le matin, mais perdait de sa puissance l'après-midi.
Après avoir analysé son installation, nous avons découvert que le système était exposé à la lumière directe du soleil, ce qui a provoqué une augmentation de la température de 15°C. En utilisant la loi des gaz idéaux, nous avons calculé que ce changement de température provoquait une variation de pression de près de 5%. Nous avons installé une isolation adéquate et le problème a été résolu immédiatement.
Applications pratiques de la loi des gaz dans la conception pneumatique
Lors de la conception de systèmes pneumatiques avec cylindres sans tigeLa loi des gaz nous aide :
- Calculer les variations de pression dues aux fluctuations de température
- Déterminer le volume requis pour les réservoirs d'air
- Prévoir les variations de la force produite dans différentes conditions
- Dimensionner les compresseurs en fonction de l'application
Quelle est la relation entre la force, la pression et la surface dans les cylindres pneumatiques ?
Il est essentiel de comprendre la relation entre la force, la pression et la surface pour choisir le bon vérin sans tige pour votre application. Cette connaissance vous permet d'obtenir les performances dont vous avez besoin sans dépassement de budget.
Le relation force-pression-surface3 dans les vérins pneumatiques est définie par F = P × A, où F est la force (N), P est la pression (Pa) et A est la surface effective (m²). Cette équation permet aux ingénieurs de calculer la force exacte des vérins sans tige à différentes pressions de fonctionnement.
Cette simple équation est à la base de tous les calculs de force pneumatique, mais il existe plusieurs considérations pratiques que de nombreux ingénieurs négligent.
Calculs de la surface effective pour différents types de cylindres
La surface effective varie en fonction du type de cylindre :
| Type de cylindre | Calcul de la surface effective | Notes |
|---|---|---|
| Simple effet | A = πr² | Zone d'alésage complet |
| Double effet (extension) | A = πr² | Zone d'alésage complet |
| Double effet (rétractation) | A = π(r² - r'²) | r' est le rayon de la tige |
| Cylindre sans tige | A = πr² | Cohérent dans les deux sens |
Facteurs d'efficacité de la force dans le monde réel
Dans la pratique, la force réelle produite est affectée par :
- Pertes par frottement: Typiquement 3-20% en fonction de la conception du joint
- Pertes de charge: Peut réduire la pression effective de 5-10%
- Effets dynamiques: Les forces d'accélération peuvent réduire la force disponible
Je me souviens d'avoir travaillé avec Sarah, une ingénieure en mécanique d'une entreprise d'emballage au Royaume-Uni. Elle concevait une nouvelle machine et avait calculé qu'elle avait besoin d'un cylindre sans tige avec un alésage de 63 mm pour obtenir la force requise. Cependant, elle n'avait pas tenu compte des pertes par frottement.
Nous lui avons recommandé de passer à un cylindre de 80 mm d'alésage, ce qui a fourni une force supplémentaire suffisante pour surmonter le frottement tout en maintenant les performances requises. Ce simple ajustement lui a évité une reconception coûteuse après l'installation.
Comparaison de la puissance théorique et de la puissance réelle de la force
Lors de la sélection de cylindres sans tige, je recommande toujours :
- Calculer la force théorique en utilisant F = P × A
- Appliquer un facteur de sécurité de 25% pour la plupart des applications
- Vérifier les calculs avec les données de performance réelles du fabricant
- Tenir compte des conditions de charge dynamique, le cas échéant
Quelle est la relation entre le débit et la vitesse dans les systèmes pneumatiques ?
Le débit et la vitesse sont des paramètres critiques qui déterminent la rapidité de réaction de votre système pneumatique. Comprendre cette relation permet d'éviter les performances lentes et de s'assurer que votre système répond aux exigences en matière de temps de cycle.
La relation entre le débit (Q) et la vitesse (v)4 dans les systèmes pneumatiques est définie par Q = v × A, où Q est le débit volumétrique, v la vitesse de l'air et A la surface de la section transversale du passage. Cette équation est essentielle pour dimensionner correctement les conduites d'air et les vannes.
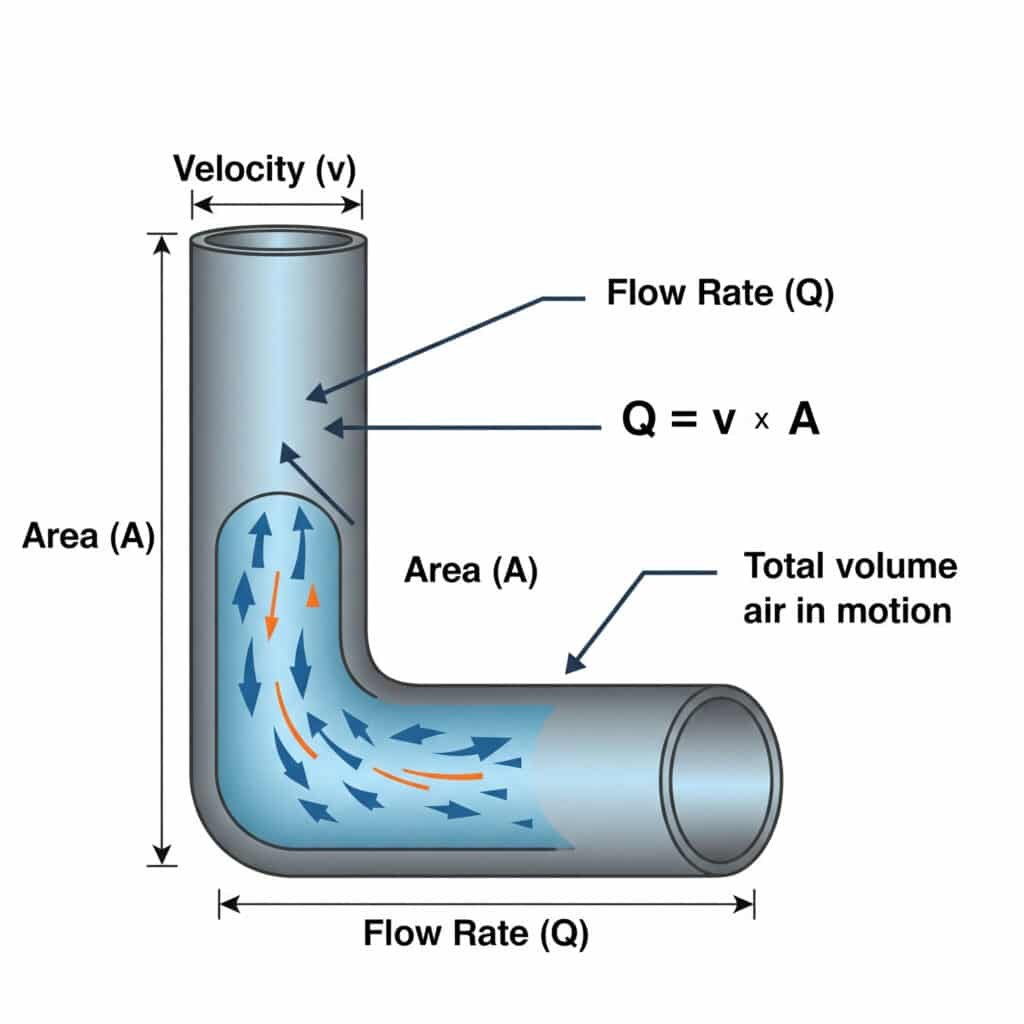
De nombreux problèmes liés aux systèmes pneumatiques proviennent d'un mauvais dimensionnement des composants d'alimentation en air. Voyons comment cette équation influe sur les performances réelles.
Débits critiques pour les composants pneumatiques courants
Les exigences en matière de débit varient d'un composant à l'autre :
| Composant | Débit typique requis | Impact du sous-dimensionnement |
|---|---|---|
| Cylindre sans tige (alésage de 25 mm) | 15-30 L/min | Fonctionnement lent, force réduite |
| Cylindre sans tige (alésage 63 mm) | 60-120 L/min | Mouvement incohérent |
| Valve de contrôle directionnel | Variable selon la taille | Chute de pression, réponse lente |
| Unité de préparation de l'air | Total du système + 30% | Fluctuations de la pression |
Comment le diamètre des tuyaux affecte-t-il la performance du système ?
Le diamètre des conduites d'air a un effet considérable sur les performances du système :
- Perte de charge: Augmente avec le carré de la vitesse
- Temps de réponse: Des lignes plus petites signifient une vitesse plus élevée mais une plus grande résistance.
- Efficacité énergétique: Des conduites plus grandes réduisent la perte de charge mais augmentent le coût
Calcul de la taille des conduites pour les systèmes pneumatiques
Pour dimensionner correctement les conduites d'air pour votre application de vérin sans tige :
- Déterminer le débit nécessaire en fonction de la taille du cylindre et de la durée du cycle
- Calculer la perte de charge maximale admissible (généralement 0,1 bar ou moins).
- Choisir un diamètre de ligne qui maintient la vitesse en dessous de 15-20 m/s
- Vérifier la capacité de débit de la vanne (Valeur Cv ou Kv5) correspond aux exigences du système
J'ai aidé un jour un client en France qui avait un mouvement de cylindre lent malgré un gros compresseur. Le problème n'était pas une production d'air insuffisante, mais le fait que ses tuyaux de 6 mm créaient une résistance excessive. Le passage à des conduites de 10 mm a immédiatement résolu le problème, augmentant le taux de cycle de sa machine de 40%.
Conclusion
La compréhension de ces trois équations pneumatiques fondamentales - la loi des gaz idéaux, la relation force-pression-surface et la connexion débit-vitesse - constitue la base d'une conception réussie des systèmes pneumatiques. En appliquant ces principes, vous pouvez sélectionner les bons composants de vérins sans tige, résoudre efficacement les problèmes et optimiser les performances du système.
FAQ sur les équations de transmission pneumatique
Qu'est-ce que la loi des gaz idéaux et pourquoi est-elle importante pour les systèmes pneumatiques ?
La loi des gaz idéaux (PV = nRT) décrit la relation entre la pression, le volume, la température et la quantité de gaz dans un système pneumatique. Elle est importante car elle aide les ingénieurs à prévoir comment des conditions changeantes (en particulier la température) affecteront les performances du système et les exigences en matière de pression.
Comment calculer la force de sortie d'un cylindre sans tige ?
Calculer la force de sortie en multipliant la pression par la surface effective (F = P × A). Pour un vérin sans tige, la surface effective est la même dans les deux sens, ce qui simplifie le calcul de la force par rapport aux vérins conventionnels qui ont des forces d'extension et de rétraction différentes.
Quelle est la différence entre le débit et la vitesse dans les systèmes pneumatiques ?
Le débit est le volume d'air qui se déplace dans un système par unité de temps (généralement en L/min), tandis que la vitesse est la vitesse à laquelle l'air se déplace dans un passage (en m/s). Ils sont liés par l'équation Q = v × A, où A est la surface de la section transversale du passage.
Comment la température affecte-t-elle les performances des systèmes pneumatiques ?
La température influe directement sur la pression, conformément à la loi des gaz idéaux. Une augmentation de 10°C de la température peut augmenter la pression d'environ 3,5% si le volume reste constant. Cela peut entraîner des variations de pression, affecter les performances des joints et modifier la force de sortie des vérins sans tige.
Quelle est la cause la plus fréquente de perte de charge dans les systèmes pneumatiques ?
Les causes les plus courantes de perte de charge sont les conduites d'air sous-dimensionnées, les raccords restrictifs et la capacité de débit inadéquate des soupapes. Selon l'équation du débit, des passages plus petits nécessitent une vitesse d'air plus élevée, ce qui augmente la résistance et la perte de charge de manière exponentielle.
Comment dimensionner correctement les conduites d'air pour un cylindre sans tige ?
Dimensionnez les conduites d'air en calculant le débit requis en fonction du volume du vérin et de la durée du cycle, puis sélectionnez un diamètre de conduite qui maintient la vitesse de l'air en dessous de 15-20 m/s afin de minimiser la perte de charge. Pour la plupart des applications de vérins sans tige, les conduites de 8 à 12 mm offrent un bon équilibre entre performance et coût.
-
Fournit une explication détaillée de la loi des gaz idéaux, l'équation fondamentale de l'état d'un gaz idéal hypothétique qui approxime le comportement de nombreux gaz dans diverses conditions. ↩
-
Explique le rôle et la valeur de la constante universelle des gaz (R) dans la loi des gaz idéaux, qui sert de constante physique reliant les échelles d'énergie aux échelles de température. ↩
-
Propose une explication fondamentale de la pression, définie comme la force appliquée perpendiculairement à la surface d'un objet par unité de surface sur laquelle cette force est répartie. ↩
-
Détaille le principe de l'équation de continuité, un concept fondamental de la dynamique des fluides qui stipule que pour un fluide incompressible, le débit massique doit être constant d'une section transversale à l'autre d'un tuyau. ↩
-
Fournit une définition technique du coefficient de débit (Cv) et du facteur de débit (Kv), qui sont des valeurs normalisées utilisées pour comparer les capacités de débit de différentes vannes. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська