
Worstelt u met inconsistente pneumatische cilindersnelheden of onverwachte impacts aan het einde van de slag? Deze veel voorkomende problemen komen vaak voort uit een slecht begrip van zuigerkinematica. Veel ingenieurs richten zich alleen op de krachtvereisten en zien de kritische bewegingsparameters over het hoofd die de systeemprestaties bepalen.
Zuiger kinematica1 hebben een directe invloed op de prestaties van pneumatische systemen door druk-snelheidsrelaties, versnellingslimieten en dempingsvereisten. Inzicht in deze principes stelt ingenieurs in staat om componenten op de juiste maat te maken, werkelijke bewegingsprofielen te voorspellen en voortijdige storingen in staafloze cilinders en andere pneumatische actuatoren te voorkomen.
In de meer dan 15 jaar dat ik bij Bepto met pneumatische systemen werk, heb ik talloze gevallen gezien waarin het begrijpen van deze fundamentele principes klanten heeft geholpen hardnekkige prestatieproblemen op te lossen en de levensduur van apparatuur met 3 tot 5 keer te verlengen.
Inhoudsopgave
- Welke druk heb je eigenlijk nodig voor beweging met constante snelheid?
- Hoe bereken je de maximaal mogelijke versnelling in pneumatische cilinders?
- Waarom is de compensatietijd belangrijk en hoe wordt hij berekend?
- Conclusie
- Veelgestelde vragen over zuiger-kinematica in pneumatische systemen
Welke druk heb je eigenlijk nodig voor beweging met constante snelheid?
Veel technici passen simpelweg de maximaal beschikbare druk toe op hun pneumatische systemen, maar deze aanpak is inefficiënt en kan leiden tot schokkerige bewegingen, overmatige slijtage en energieverspilling.
De druk die nodig is voor een beweging met constante snelheid in een pneumatische cilinder wordt berekend met P = (F + Fr)/A, waarbij P de druk is, F de kracht van de externe belasting, Fr de wrijvingsweerstand en A het zuigeroppervlak. Deze berekening zorgt voor een soepele, efficiënte werking zonder overmatige druk die energie verspilt en de slijtage van onderdelen versnelt.
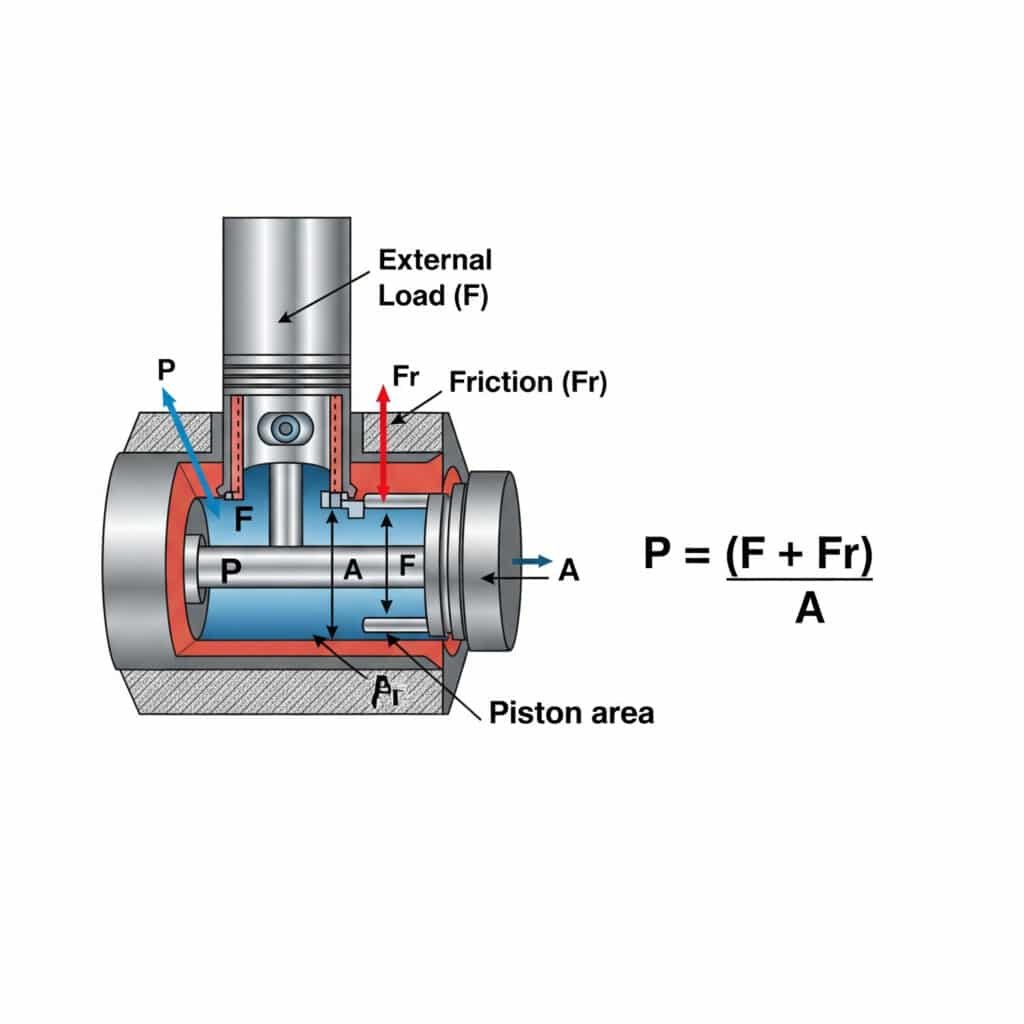
Inzicht in de drukvereisten voor beweging met constante snelheid heeft praktische gevolgen voor het ontwerp en de werking van het systeem. Ik zal dit uitsplitsen in bruikbare inzichten.
Factoren die de drukvereisten voor constante snelheid beïnvloeden
De druk die nodig is om de snelheid constant te houden, hangt af van verschillende factoren:
| Factor | Invloed op drukvereisten | Praktische overwegingen |
|---|---|---|
| Externe belasting | Directe lineaire relatie | Varieert met oriëntatie en externe krachten |
| Wrijving | Voegt toe aan de vereiste druk | Veranderingen door slijtage en smering van afdichtingen |
| Zuigeroppervlak | Omgekeerd evenredig | Grotere boring = lagere drukvereisten |
| Beperkingen luchttoevoer | Drukverliezen in leidingen/kleppen | Componenten dimensioneren voor minimale drukval |
| Tegendruk | Tegen de motie | Overweeg de uitlaatgasstroomcapaciteit |
Minimale druk voor stabiele beweging berekenen
De minimale druk bepalen die nodig is voor een stabiele beweging:
- Bereken de kracht die nodig is om de externe belasting te overwinnen
- Tel de wrijvingskracht op (meestal 3-20% van de maximale kracht)
- Delen door het effectieve zuigeroppervlak
- Voeg een stabiliteitsfactor toe (meestal 10-30%)
Bijvoorbeeld in een staafloze cilinder met een boring van 40 mm, een belasting van 10 kg en wrijving van 15%:
| Parameter | Berekening | Resultaat |
|---|---|---|
| Belastingskracht | 10kg × 9,81m/s² | 98.1N |
| Wrijvingskracht | 15% maximale kracht bij 6 bar | ~45N |
| Totale kracht | 98,1N + 45N | 143.1N |
| Zuigeroppervlak | π × (0,02m)² | 0.00126m² |
| Minimum druk | 143,1N ÷ 0,00126m² | 113,571 Pa (1,14 bar) |
| Met 20% Stabiliteitsfactor | 1,14 bar × 1,2 | 1,37 bar |
Toepassing in de praktijk: Energiebesparing door drukoptimalisatie
Vorig jaar werkte ik met Robert, een productie-ingenieur in een meubelfabriek in Michigan. Zijn geautomatiseerde assemblagelijn gebruikte cilinders zonder stangen die op de volledige toevoerdruk van 6 bar werkten, ongeacht de belasting.
Na analyse van zijn toepassing stelden we vast dat de meeste bewegingen slechts 2,5-3 bar nodig hadden voor een stabiele werking. Door proportionele drukregelaarshebben we het luchtverbruik met 40% verlaagd bij gelijkblijvende cyclustijd. Dit bespaarde jaarlijks ongeveer $12.000 aan energiekosten, terwijl de slijtage van de afdichtingen werd verminderd en de onderhoudsintervallen werden verlengd.
Snelheid-drukrelatie in echte systemen
In de praktijk is de relatie tussen druk en snelheid niet perfect lineair door:
- Stroombeperkingen: Klep- en poortafmetingen beïnvloeden de maximaal haalbare snelheid
- Samendrukbaarheidseffecten: Lucht is samendrukbaar, waardoor de versnelling achterblijft
- Stick-slipverschijnselen: Wrijvingseigenschappen veranderen met de snelheid
- Traagheidseffecten: Versnelling van de massa vereist extra kracht/druk
Hoe bereken je de maximaal mogelijke versnelling in pneumatische cilinders?
Inzicht in versnellingslimieten is cruciaal voor het voorkomen van overmatige schokken, trillingen en voortijdig defect raken van onderdelen in pneumatische systemen.
De maximaal mogelijke versnelling in een pneumatische cilinder wordt berekend met a = (P × A - F - Fr)/m, waarbij a de versnelling is, P de druk, A het zuigeroppervlak, F de externe belasting, Fr de wrijvingsweerstand en m de bewegende massa. Deze vergelijking definieert de fysieke grenzen van hoe snel een pneumatische actuator een beweging kan starten of stoppen.
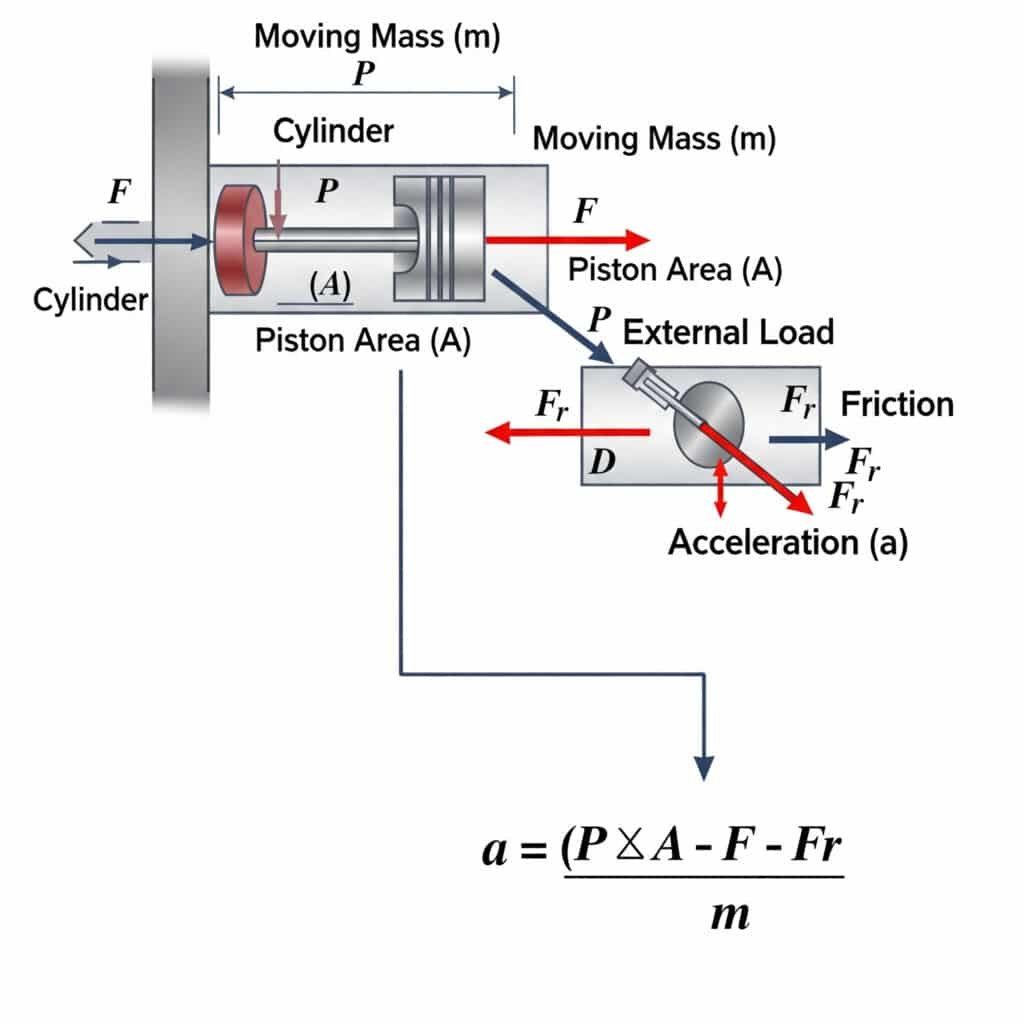
De theoretische versnellingslimieten hebben belangrijke praktische implicaties voor het systeemontwerp en de componentenselectie.
Afleiding van de versnellingsgrensvergelijking
De vergelijking voor de versnellingslimiet komt uit De tweede wet van Newton2 (F = ma):
- De nettokracht die beschikbaar is voor versnelling is: Fnet = Fdruk - Flast - Fwrijving
- Fdruk = P × A
- Daarom: a = Fnet/m = (P × A - F - Fr)/m
Praktische versnellingslimieten voor verschillende cilindertypes
Verschillende cilinderontwerpen hebben verschillende praktische versnellingslimieten:
| Type cilinder | Typische max. versnelling | Beperkende factoren |
|---|---|---|
| Standaard staafcilinder | 10-15 m/s² | Stangknik, lagerbelastingen |
| Staafloze cilinder (magnetisch) | 8-12 m/s² | Magnetische koppelsterkte |
| Stangloze cilinder (mechanisch) | 15-25 m/s² | Ontwerp afdichting/lager, interne wrijving |
| Geleide cilinder | 20-30 m/s² | Stijfheid van het geleidingssysteem, draagvermogen |
| Slagcilinder | 50-100+ m/s² | Speciaal ontworpen voor hoge acceleratie |
Overwegingen met betrekking tot massa in versnellingsberekeningen
Bij het berekenen van versnelling is het essentieel om alle bewegende massa's mee te nemen:
- Zuigerassemblage: Inclusief zuiger, afdichtingen en verbindingselementen
- Laadmassa: Externe belasting die wordt verplaatst
- Effectieve massa van bewegende lucht: Vaak verwaarloosbaar, maar relevant bij hogesnelheidstoepassingen
- Toegevoegde massa door montageonderdelen: Beugels, sensoren, enz.
Ik heb ooit een klant in Frankrijk geholpen die last had van mysterieuze storingen in zijn staafloze cilindersysteem. De cilinder had de juiste maat voor de opgegeven belasting van 15 kg, maar begaf het steeds na een paar duizend cycli.
Na onderzoek ontdekten we dat hij vergeten was rekening te houden met de 12 kg massa van de montageplaat en hulpstukken. De werkelijke bewegende massa was bijna het dubbele van wat hij had berekend, waardoor de versnellingskrachten de ontwerplimieten van de cilinder overschreden. Na het upgraden naar een grotere cilinder stopten de storingen volledig.
Methoden voor versnellingsregeling
De acceleratie binnen veilige grenzen houden:
- Stroomregelkleppen: Beperk het debiet tijdens de eerste beweging
- Proportionele kleppen: Zorg voor een gecontroleerde drukverhoging
- Versnelling in meerdere fasen: Stapsgewijze drukverhoging gebruiken
- Mechanische demping: Externe schokdempers toevoegen
- Elektronische besturing: Gebruik servo-pneumatische systemen3 met versnellingsfeedback
Waarom is de compensatietijd belangrijk en hoe wordt hij berekend?
Een goede demping aan het einde van de slag is essentieel voor het voorkomen van impactschade, het verminderen van geluid en het verlengen van de levensduur van pneumatische cilinders. Inzicht in de dempingstijd helpt ingenieurs bij het ontwerpen van systemen die de cyclustijd in balans brengen met de levensduur van componenten.
De dempingstijd in pneumatische cilinders wordt berekend met de vergelijking t = √(2s/a), waarbij t de tijd is, s de dempingsslaglengte en a de vertraging. Deze tijd geeft aan hoe lang het duurt om de bewegende massa veilig af te remmen voor de impact, wat cruciaal is om schade aan de cilinder en de aangesloten onderdelen te voorkomen.

Laten we eens kijken naar de praktische aspecten van dempingtijdberekeningen en hun implicaties voor het systeemontwerp.
De fysica achter pneumatische demping
Pneumatische demping werkt door gecontroleerde luchtcompressie en beperkte uitlaat:
- Als de zuiger de kussenkamer ingaat, wordt het uitlaatpad beperkt
- De ingesloten lucht wordt samengeperst, waardoor de tegendruk toeneemt
- Deze tegendruk creëert een tegenkracht die de zuiger vertraagt.
- Het vertragingsprofiel is afhankelijk van het ontwerp en de afstelling van het kussen
Optimale dempingstijd berekenen
De optimale dempingstijd zorgt voor een evenwicht tussen schokpreventie en cyclustijdsefficiëntie:
| Parameter | Formule | Voorbeeld |
|---|---|---|
| Dempingsafstand | Gebaseerd op cilinderontwerp | 15 mm (typisch voor een boring van 40 mm) |
| Vereiste vertraging | a = v²/(2s) | Voor v=0,5m/s, s=15mm: a = 8,33m/s² |
| Dempingstijd | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Drukopbouw | P = P₀(V₀/V)^γ | Afhankelijk van de kussenkamergeometrie |
Factoren die de dempingsprestaties beïnvloeden
Verschillende factoren beïnvloeden de daadwerkelijke dempingsprestaties:
- Ontwerp met kussenafdichting: Beïnvloedt luchtlekkage tijdens demping
- Naaldklep afstellen: Regelt de uitlaatbeperking
- Bewegende massa: Zwaardere ladingen vereisen een langere dempingstijd
- Naderingssnelheid: Hogere snelheden vereisen een langere kussenafstand
- Bedrijfsdruk: Beïnvloedt de maximaal beschikbare tegenkracht
Soorten kussens en hun toepassingen
Verschillende dempingsmechanismen zijn geschikt voor verschillende toepassingen:
| Type demping | Kenmerken | Beste toepassingen |
|---|---|---|
| Vaste demping | Eenvoudig, niet verstelbaar | Lichte belastingen, consistente werking |
| Verstelbare demping | Afstembaar met naaldkleppen | Wisselende belastingen, flexibele toepassingen |
| Zelfaanpassende demping | Past zich aan verschillende omstandigheden aan | Snelheden en belastingen veranderen |
| Externe schokdempers | Hoge energieabsorptie | Zware ladingen, hoge snelheden |
| Elektronische demping | Nauwkeurig geregelde vertraging | Servo-pneumatische systemen |
Casestudie: Optimaliseren van demping in toepassingen met hoge cycli
Onlangs werkte ik met Thomas, een ontwerpingenieur bij een fabrikant van auto-onderdelen in Duitsland. Zijn assemblagelijn gebruikte cilinders zonder stangen die 45 cycli per minuut draaiden, maar hij had regelmatig last van defecte afdichtingen en schade aan de montagebeugel.
Analyse toonde aan dat de dempingstijd te kort was voor de bewegende massa, waardoor er aan het einde van de slag botskrachten van bijna 3G werden veroorzaakt. Door de dempingsslag te verhogen van 12 naar 20 mm en de naaldklepinstellingen te optimaliseren, verlengden we de dempingstijd van 0,04 naar 0,07 seconden.
Deze ogenschijnlijk kleine verandering verminderde de botskrachten met meer dan 60%, elimineerde de schade aan de beugel volledig en verlengde de levensduur van de afdichting van 3 maanden tot meer dan een jaar - en dat alles met behoud van de vereiste cyclustijd.
Praktische afstelprocedure voor demping
Voor optimale dempingsprestaties in cilinders zonder stang:
- Begin met de kussenkleppen volledig open (minimale restrictie)
- Sluit de dempingsklep geleidelijk tot een soepele vertraging is bereikt.
- Test met minimale en maximale verwachte belasting
- Controleer de dempingsprestaties over het volledige snelheidsbereik
- Luister naar contactgeluiden die duiden op onvoldoende demping
- Meet de werkelijke vertragingstijd om de berekeningen te bevestigen
Conclusie
Inzicht in de principes van zuigerkinematica - van drukvereisten voor constante snelheid tot versnellingslimieten en berekening van dempingstijden - is essentieel voor het ontwerpen van efficiënte, betrouwbare pneumatische systemen. Door deze principes toe te passen op uw toepassingen met staafloze cilinders kunt u de prestaties optimaliseren, het energieverbruik verlagen en de levensduur van componenten aanzienlijk verlengen.
Veelgestelde vragen over zuiger-kinematica in pneumatische systemen
Welke druk heb ik nodig voor een specifieke cilindersnelheid?
De benodigde druk hangt af van de belasting, de wrijving en het cilinderoppervlak. Bereken de druk met P = (F + Fr)/A, waarbij F de kracht van de externe belasting is, Fr de wrijvingsweerstand en A het zuigeroppervlak. Voor een typische cilinder zonder stang die een last van 10 kg horizontaal verplaatst, heb je ongeveer 1,5-2 bar nodig voor een stabiele beweging bij matige snelheden.
Hoe snel kan een pneumatische cilinder versnellen?
De maximale versnelling van een pneumatische cilinder wordt berekend met a = (P × A - F - Fr)/m. Typische cilinders zonder staaf kunnen een versnelling van 10-25 m/s² bereiken, afhankelijk van het ontwerp. Dit komt neer op het bereiken van een snelheid van 0,5 m/s in ongeveer 20-50 milliseconden onder optimale omstandigheden.
Welke factoren beperken de maximumsnelheid van een cilinder zonder stang?
De maximale snelheid wordt beperkt door de doorstroomcapaciteit van de klep, het luchttoevoervolume, de afmetingen van de poort, de dempingsmogelijkheden en het ontwerp van de afdichting. De meeste standaard staafloze cilinders zijn ontworpen voor maximumsnelheden van 0,8-1,5 m/s, hoewel gespecialiseerde ontwerpen voor hoge snelheden 2-3 m/s kunnen bereiken.
Hoe bereken ik de juiste demping voor mijn toepassing?
Bereken de juiste demping door de kinetische energie (KE = ½mv²) van uw bewegende last te bepalen en zorg ervoor dat uw dempingssysteem deze energie kan absorberen. De dempingstijd moet worden berekend met t = √(2s/a), waarbij s de kussenafstand is en a de gewenste vertragingssnelheid.
Wat gebeurt er als mijn pneumatische cilinder te snel versnelt?
Overmatige acceleratie kan leiden tot mechanische spanning op montagecomponenten, vroegtijdige slijtage van afdichtingen, meer trillingen en lawaai, mogelijke verschuiving of beschadiging van de belasting en verminderde nauwkeurigheid van het systeem. Het kan ook leiden tot schokkerige bewegingen die de productkwaliteit in precisietoepassingen aantasten.
Hoe beïnvloedt de oriëntatie van de lading de druk die nodig is voor beweging?
De oriëntatie van de last heeft een aanzienlijke invloed op de drukvereisten. Verticale lasten die tegen de zwaartekracht in bewegen, hebben extra druk nodig om de zwaartekracht te overwinnen (P = F/A + Fg/A + Fr/A). Horizontale lasten hoeven alleen wrijving en traagheid te overwinnen. Hellende lasten vallen tussen deze uitersten in op basis van de sinus van de hoek.
-
Biedt een fundamentele uitleg van kinematica, de tak van mechanica die de beweging van voorwerpen beschrijft zonder rekening te houden met de krachten die de beweging veroorzaken.
elektronisch ingangssignaal, waardoor geavanceerde pneumatische regeling mogelijk is. ↩ -
Gaat in op de tweede wet van Newton (F=ma), het fundamentele principe van de natuurkunde dat de kracht die op een voorwerp werkt, relateert aan de massa en versnelling ervan, en dat de basis vormt voor alle dynamische berekeningen. ↩
-
Beschrijft servo-pneumatiek, een geavanceerde besturingstechnologie die de kracht van pneumatiek combineert met de precisie van elektronische besturing met gesloten lus voor zeer nauwkeurige positionering en bewegingsprofielen. ↩


