
Many facility managers struggle with excessive energy costs, frequent compressor failures, and inadequate air pressure for their pneumatic systems, not realizing that incorrect compression ratio calculations are causing inefficient operation that can increase energy costs by 30-50% and dramatically reduce equipment life.
Compressor compression ratio is calculated by dividing absolute discharge pressure1 by absolute inlet pressure (CR = P_discharge/P_inlet), typically ranging from 3:1 to 12:1 for industrial applications, with optimal ratios of 7:1 to 9:1 providing the best balance of efficiency, reliability, and performance for rodless cylinders and pneumatic systems.
Two weeks ago, I received an urgent call from Thomas, a maintenance manager at an Ohio manufacturing plant, whose new compressor was consuming 40% more energy than expected and failing to maintain adequate pressure for his rodless cylinder systems, until we discovered his compression ratio was incorrectly calculated at 15:1 instead of the optimal 8:1, costing his facility $3,200 monthly in excess energy costs.
Table of Contents
- What Is Compressor Compression Ratio and Why Does It Matter for System Performance?
- How Do You Calculate Compression Ratio Using Absolute Pressures?
- What Are the Optimal Compression Ratios for Different Compressor Types and Applications?
- How Does Compression Ratio Impact Energy Efficiency and Equipment Life?
What Is Compressor Compression Ratio and Why Does It Matter for System Performance?
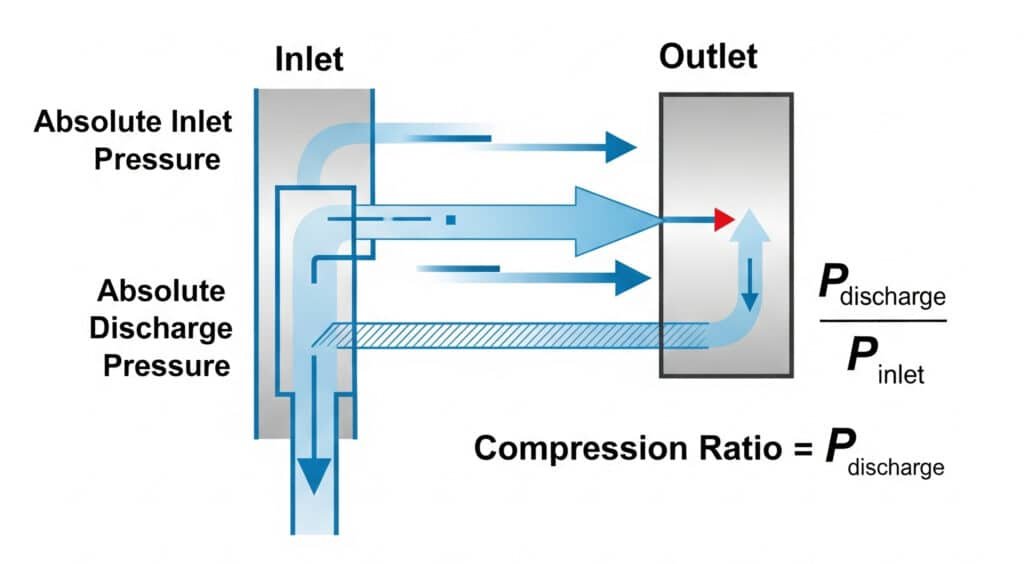
Compressor compression ratio represents the relationship between inlet and discharge pressures, serving as a critical parameter that determines compressor efficiency, energy consumption, and reliability in pneumatic systems.
Compression ratio is the ratio of absolute discharge pressure to absolute inlet pressure, typically expressed as X:1 (such as 8:1), with higher ratios requiring more energy per unit of compressed air while lower ratios may not provide adequate pressure for pneumatic applications like rodless cylinders that require 80-150 PSI operating pressure.
Fundamental Definition and Physics
Compression ratio quantifies how much the air is compressed during the compression process, directly affecting the work required and heat generated.
Mathematical Definition: CR = P_absolute_discharge / P_absolute_inlet
Where pressures must be expressed in absolute terms (PSIA) rather than gauge pressure (PSIG). This distinction is critical because gauge pressure readings don’t account for atmospheric pressure.
Physical Significance: Higher compression ratios mean the air molecules are compressed into a smaller volume, requiring more work input and generating more heat. This relationship follows the ideal gas law and thermodynamic principles governing compression processes.
Impact on System Performance
Compression ratio directly affects multiple aspects of pneumatic system performance:
Energy Consumption: Power requirements increase exponentially with compression ratio. A compressor operating at 12:1 ratio consumes approximately 50% more energy than one operating at 8:1 ratio for the same air delivery.
Air Quality: Higher compression ratios generate more heat and moisture, requiring enhanced cooling and air treatment systems to maintain air quality standards for sensitive pneumatic applications.
Equipment Reliability: Excessive compression ratios increase component stress, reduce service life, and increase maintenance requirements across the entire pneumatic system.
| Compression Ratio | Energy Impact | Heat Generation | Typical Applications |
|---|---|---|---|
| 3:1 – 5:1 | Low energy use | Minimal heat | Low-pressure applications |
| 6:1 – 8:1 | Optimal efficiency | Moderate heat | General industrial use |
| 9:1 – 12:1 | High energy use | Significant heat | High-pressure applications |
| 13:1+ | Very high energy | Excessive heat | Specialized applications only |
Relationship to Pneumatic Component Performance
The compression ratio affects how well pneumatic components, including rodless cylinders, perform in the system:
Operating Pressure Stability: Proper compression ratios ensure consistent pressure delivery, critical for accurate positioning and smooth operation of rodless cylinders and other precision pneumatic components.
Air Flow Characteristics: Compression ratio affects the compressor’s ability to deliver adequate flow rates during peak demand periods, preventing pressure drops that can cause erratic cylinder operation.
System Response Time: Optimal compression ratios enable faster pressure recovery after high-demand events, maintaining system responsiveness for automated applications.
Common Misconceptions
Several misconceptions about compression ratio can lead to poor system design:
Gauge vs. Absolute Pressure: Using gauge pressure instead of absolute pressure in calculations results in incorrect compression ratios and poor system performance.
Higher is Always Better: Many assume higher compression ratios provide better performance, but excessive ratios waste energy and reduce reliability.
Single-Stage Limitations: Attempting to achieve high compression ratios with single-stage compressors leads to inefficiency and premature failure.
At Bepto, we help customers optimize their compressed air systems for our rodless cylinder applications, ensuring compression ratios are properly calculated and matched to system requirements for maximum efficiency and reliability.
How Do You Calculate Compression Ratio Using Absolute Pressures?
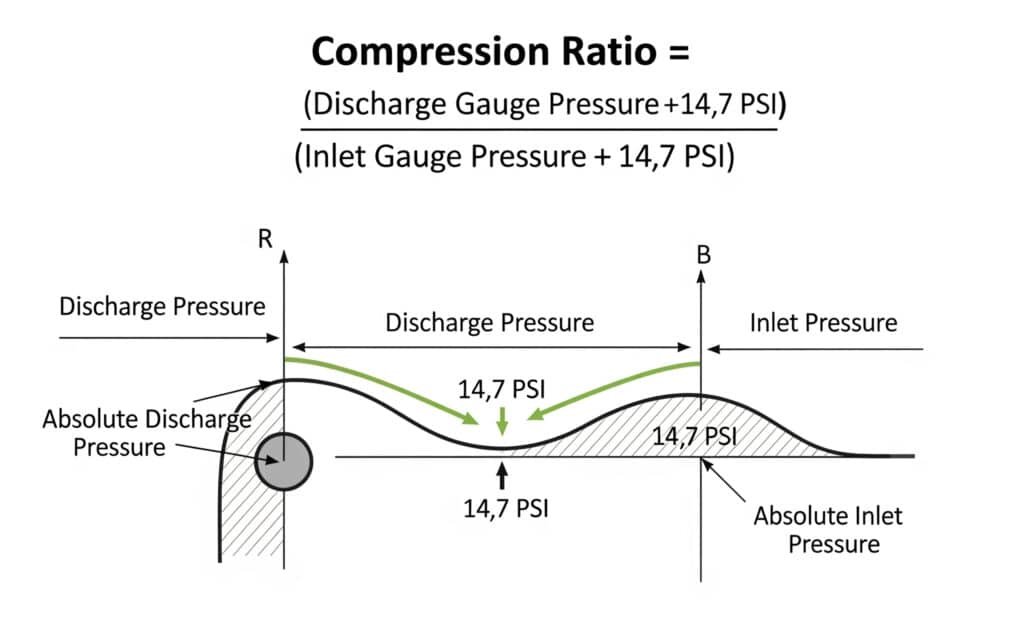
Accurate compression ratio calculation requires converting gauge pressures to absolute pressures and applying the correct mathematical formula to ensure optimal compressor selection and operation.
Calculate compression ratio by adding atmospheric pressure (14.7 PSI at sea level) to both inlet and discharge gauge pressures to get absolute pressures, then divide discharge absolute pressure by inlet absolute pressure: CR = (P_discharge_gauge + 14.7) / (P_inlet_gauge + 14.7), with corrections for altitude and atmospheric conditions.
Step-by-Step Calculation Process
Proper compression ratio calculation follows a systematic process to ensure accuracy:
Step 1: Determine Inlet Conditions
- Measure or estimate inlet gauge pressure (typically 0 PSIG for atmospheric inlet)
- Account for inlet restrictions, filters, or elevation effects
- Note ambient temperature and humidity conditions
Step 2: Determine Discharge Pressure
- Identify required system pressure (typically 80-150 PSIG for pneumatic systems)
- Add pressure drops through aftercoolers, dryers, and distribution system
- Include safety margin for pressure variations
Step 3: Convert to Absolute Pressures
- Add atmospheric pressure to both inlet and discharge gauge pressures
- Use local atmospheric pressure (varies with altitude)
- Standard atmospheric pressure = 14.7 PSIA at sea level
Step 4: Calculate Compression Ratio
CR = P_absolute_discharge / P_absolute_inlet
Practical Calculation Examples
Example 1: Standard Industrial Application
- System requirement: 100 PSIG
- Inlet conditions: Atmospheric (0 PSIG)
- Atmospheric pressure: 14.7 PSIA (sea level)
Calculation:
- P_absolute_discharge = 100 + 14.7 = 114.7 PSIA
- P_absolute_inlet = 0 + 14.7 = 14.7 PSIA
- CR = 114.7 / 14.7 = 7.8:1
Example 2: High-Altitude Installation
- System requirement: 125 PSIG
- Inlet conditions: Atmospheric (0 PSIG)
- Altitude: 5,000 feet (atmospheric pressure = 12.2 PSIA)
Calculation:
- P_absolute_discharge = 125 + 12.2 = 137.2 PSIA
- P_absolute_inlet = 0 + 12.2 = 12.2 PSIA
- CR = 137.2 / 12.2 = 11.2:1
Altitude Correction Factors
Atmospheric pressure varies significantly with altitude, affecting compression ratio calculations:
| Altitude (feet) | Atmospheric Pressure (PSIA) | Correction Factor |
|---|---|---|
| Sea Level | 14.7 | 1.00 |
| 1,000 | 14.2 | 0.97 |
| 2,500 | 13.4 | 0.91 |
| 5,000 | 12.2 | 0.83 |
| 7,500 | 11.1 | 0.76 |
| 10,000 | 10.1 | 0.69 |
Temperature and Humidity Effects
Environmental conditions affect compression ratio calculations and compressor performance:
Temperature Impact: Higher inlet temperatures reduce air density, affecting volumetric efficiency and requiring corrections for accurate calculations.
Humidity Effects: Water vapor content affects the effective gas properties during compression, particularly important in high-humidity environments.
Seasonal Variations: Atmospheric pressure and temperature changes throughout the year can affect compression ratios by ±5-10%.
Multi-Stage Compression Calculations
Multi-stage compressors divide the total compression ratio across multiple stages:
Two-Stage Example:
- Total compression ratio: 9:1
- Optimal stage ratio: √9 = 3:1 per stage
- First stage: 14.7 to 44.1 PSIA (3:1 ratio)
- Second stage: 44.1 to 132.3 PSIA (3:1 ratio)
- Total: 132.3 / 14.7 = 9:1
Benefits of Multi-Stage Design:
- Improved efficiency through intercooling
- Reduced discharge temperatures
- Better moisture removal between stages
- Extended equipment life
Common Calculation Errors
Avoid these frequent mistakes in compression ratio calculations:
| Error Type | Incorrect Method | Correct Method | Impact |
|---|---|---|---|
| Using Gauge Pressure | CR = 100/0 = ∞ | CR = 114.7/14.7 = 7.8:1 | Completely wrong ratio |
| Ignoring Altitude | Using 14.7 PSIA at 5,000 ft | Using 12.2 PSIA at 5,000 ft | 35% error in ratio |
| Neglecting System Losses | Using required pressure | Adding distribution losses | Undersized compressor |
| Wrong Inlet Pressure | Assuming perfect vacuum | Using actual inlet conditions | Overestimated ratio |
Verification Methods
Verify compression ratio calculations through multiple approaches:
Manufacturer Data: Compare calculated ratios with compressor manufacturer specifications and performance curves.
Field Measurements: Use calibrated pressure gauges to measure actual inlet and discharge pressures during operation.
Performance Testing: Monitor compressor efficiency and energy consumption to validate calculated ratios.
System Analysis: Evaluate overall system performance to ensure compression ratios meet application requirements.
Susan, a facilities engineer at a Michigan automotive plant, contacted us about efficiency problems with her compressed air system. “I was calculating compression ratio using gauge pressures and getting impossible results,” she explained. “Once we corrected the calculation to use absolute pressures, we found our actual ratio was 11.2:1 instead of the 8:1 we thought we had. By adjusting our system pressure requirements and adding a second stage, we reduced our energy consumption by 28% while improving air quality for our rodless cylinder applications.”
What Are the Optimal Compression Ratios for Different Compressor Types and Applications?
Different compressor technologies and pneumatic applications require specific compression ratios to achieve optimal efficiency, reliability, and performance in industrial systems.
Optimal compression ratios vary by compressor type: reciprocating compressors perform best at 6:1-8:1 per stage, rotary screw compressors at 8:1-12:1, centrifugal compressors at 3:1-4:1 per stage, with pneumatic applications like rodless cylinders typically requiring system ratios of 7:1-9:1 for optimal balance of efficiency and performance.
Reciprocating Compressor Optimization
Reciprocating compressors have specific compression ratio limits based on their mechanical design and thermodynamic characteristics.
Single-Stage Limits: Single-stage reciprocating compressors should not exceed 8:1 compression ratio due to excessive discharge temperatures and reduced volumetric efficiency2. Optimal performance occurs at 6:1-7:1 ratios.
Discharge Temperature Considerations: Higher compression ratios generate excessive heat, with discharge temperatures following the relationship: T_discharge = T_inlet × (CR)^0.283 for adiabatic compression.
Volumetric Efficiency Impact: Compression ratio directly affects volumetric efficiency according to: ηv = 1 – C × [(CR)^(1/n) – 1], where C is clearance volume percentage and n is the polytropic exponent3.
| Compression Ratio | Discharge Temp (°F) | Volumetric Efficiency | Performance Rating |
|---|---|---|---|
| 4:1 | 250°F | 85% | Good |
| 6:1 | 320°F | 78% | Optimal |
| 8:1 | 380°F | 70% | Maximum recommended |
| 10:1 | 430°F | 60% | Poor efficiency |
| 12:1 | 480°F | 50% | Unacceptable |
Rotary Screw Compressor Characteristics
Rotary screw compressors can handle higher compression ratios due to their continuous compression process and built-in cooling.
Optimal Operating Range: Most rotary screw compressors operate efficiently at compression ratios of 8:1 to 12:1, with peak efficiency typically occurring around 9:1-10:1.
Oil-Injected vs. Oil-Free: Oil-injected units can handle higher ratios (up to 15:1) due to internal cooling, while oil-free units are limited to 8:1-10:1 ratios.
Variable Speed Drive Benefits: VSD-controlled4 screw compressors can optimize compression ratios automatically based on demand, improving overall system efficiency by 15-30%.
Centrifugal Compressor Applications
Centrifugal compressors use dynamic compression principles, requiring different optimization approaches.
Stage Limitations: Individual stages are limited to 3:1-4:1 compression ratios due to aerodynamic constraints and surge limitations.
Multi-Stage Design: High-pressure applications require multiple stages with intercooling, typically 2-4 stages for industrial pneumatic systems.
Flow Rate Dependencies: Centrifugal compressors are most efficient at high flow rates (>1000 CFM), making them suitable for large pneumatic systems with multiple rodless cylinders and other components.
Application-Specific Requirements
Different pneumatic applications have specific compression ratio requirements for optimal performance:
Standard Pneumatic Tools: Require 90-100 PSIG (compression ratio 7:1-8:1) for adequate power and efficiency.
Rodless Cylinder Applications: Optimal performance at 100-125 PSIG (compression ratio 8:1-9:1) for smooth operation and precise positioning.
High-Precision Applications: May require 150+ PSIG (compression ratio 11:1+) for adequate force and stiffness, but require careful system design.
Process Applications: Food processing, pharmaceutical, and other sensitive applications may require specific pressure ranges regardless of efficiency considerations.
Multi-Stage System Design
Multi-stage compression optimizes efficiency for high compression ratio applications:
Optimal Stage Ratios: For maximum efficiency, stage ratios should be approximately equal: Stage Ratio = (Total CR)^(1/n) where n is the number of stages.
Intercooling Benefits: Cooling between stages reduces power consumption by 15-25% and improves air quality by removing moisture.
Pressure Ratio Distribution: Unequal stage ratios may be used to optimize specific performance characteristics or accommodate equipment limitations.
| Total Ratio | Single Stage | Two Stage | Three Stage | Efficiency Gain |
|---|---|---|---|---|
| 6:1 | 6:1 | 2.45:1 each | 1.82:1 each | 5-10% |
| 9:1 | 9:1 | 3:1 each | 2.08:1 each | 15-20% |
| 12:1 | Not recommended | 3.46:1 each | 2.29:1 each | 25-30% |
| 16:1 | Not recommended | 4:1 each | 2.52:1 each | 30-35% |
Energy Efficiency Optimization
Compression ratio selection significantly impacts energy consumption and operating costs:
Specific Power Consumption: Power requirements increase exponentially with compression ratio, following approximately: Power ∝ (CR)^0.283 for adiabatic compression5.
System Pressure Optimization: Operating at the lowest practical system pressure reduces compression ratio and energy consumption while maintaining adequate performance for pneumatic components.
Load Management: Variable compression ratios through control systems can optimize energy consumption based on actual demand patterns.
Reliability Considerations
Compression ratio affects equipment reliability and maintenance requirements:
Component Stress: Higher ratios increase mechanical stress on valves, pistons, and other components, reducing service life.
Maintenance Intervals: Compressors operating at optimal ratios typically require 30-50% less maintenance than those operating at excessive ratios.
Failure Modes: Common failures associated with excessive compression ratios include valve failures, bearing problems, and cooling system issues.
Selection Guidelines
Use these guidelines for optimal compression ratio selection:
Step 1: Determine minimum required system pressure for pneumatic components
Step 2: Add pressure drops for distribution, treatment, and safety margins
Step 3: Calculate compression ratio using absolute pressures
Step 4: Compare with compressor type limitations and efficiency curves
Step 5: Consider multi-stage design if single-stage limits are exceeded
Step 6: Validate selection through energy and reliability analysis
At Bepto, we work with customers to optimize their compressed air systems for our rodless cylinder applications, ensuring compression ratios are properly matched to both compressor capabilities and pneumatic component requirements for maximum efficiency and reliability.
How Does Compression Ratio Impact Energy Efficiency and Equipment Life?
Compression ratio has a profound impact on both energy consumption and equipment reliability, with optimal ratios providing significant cost savings and extended service life compared to poorly designed systems.
Compression ratio affects energy efficiency exponentially, with power consumption increasing by approximately 7-10% for each 1:1 increase in ratio above optimal levels, while excessive ratios (>12:1 single-stage) can reduce equipment life by 50-70% through increased component stress, higher operating temperatures, and accelerated wear patterns.
Energy Consumption Relationships
The relationship between compression ratio and energy consumption follows well-established thermodynamic principles that can be quantified and optimized.
Theoretical Power Requirements: For adiabatic compression, the theoretical power follows: P = (n/(n-1)) × P₁ × V₁ × [(P₂/P₁)^((n-1)/n) – 1]
Where:
- P = Power required
- n = Polytropic exponent (typically 1.3-1.4 for air)
- P₁, P₂ = Inlet and discharge pressures
- V₁ = Inlet volume flow rate
Practical Energy Impact: Real-world energy consumption increases more rapidly than theoretical calculations due to efficiency losses, heat generation, and mechanical friction.
| Compression Ratio | Relative Power Consumption | Energy Cost Impact | Efficiency Rating |
|---|---|---|---|
| 6:1 | 100% (baseline) | $1,000/month | Optimal |
| 8:1 | 118% | $1,180/month | Good |
| 10:1 | 140% | $1,400/month | Acceptable |
| 12:1 | 165% | $1,650/month | Poor |
| 15:1 | 200% | $2,000/month | Unacceptable |
Heat Generation and Cooling Requirements
Higher compression ratios generate significantly more heat, requiring additional cooling capacity and energy consumption.
Temperature Rise Calculation: Discharge temperature increases according to: T₂ = T₁ × (CR)^((γ-1)/γ) where γ is the specific heat ratio (1.4 for air).
Cooling System Impact: Higher compression ratios require:
- Larger intercoolers and aftercoolers
- Higher cooling water flow rates
- More powerful cooling fans
- Additional heat exchangers
Secondary Energy Costs: Cooling systems can consume 15-25% additional energy for every 2:1 increase in compression ratio above optimal levels.
Equipment Life and Reliability Impact
Compression ratio directly affects component stress levels and service life across the entire compressed air system.
Mechanical Stress Factors: Higher ratios increase:
- Cylinder pressures and forces
- Bearing loads and wear rates
- Valve stress and fatigue cycles
- Seal pressure differentials
Component Life Relationships: Service life typically decreases exponentially with compression ratio:
| Component | Life at 7:1 Ratio | Life at 10:1 Ratio | Life at 13:1 Ratio | Failure Mode |
|---|---|---|---|---|
| Intake Valves | 8,000 hours | 5,500 hours | 3,200 hours | Fatigue cracking |
| Discharge Valves | 6,000 hours | 3,800 hours | 2,100 hours | Thermal stress |
| Piston Rings | 12,000 hours | 8,500 hours | 4,800 hours | Wear and blowby |
| Bearings | 15,000 hours | 11,000 hours | 6,500 hours | Load and heat |
| Seals | 10,000 hours | 6,800 hours | 3,500 hours | Pressure differential |
Maintenance Cost Analysis
Operating at excessive compression ratios dramatically increases maintenance requirements and costs.
Increased Maintenance Frequency: Higher ratios require:
- More frequent oil changes due to thermal breakdown
- Earlier valve replacements due to stress
- Increased bearing maintenance from higher loads
- More frequent cooling system service
Maintenance Cost Comparison:
- Optimal ratio (7:1): $0.02 per operating hour
- High ratio (10:1): $0.035 per operating hour (75% increase)
- Excessive ratio (13:1): $0.055 per operating hour (175% increase)
Air Quality Impact
Compression ratio affects the quality of compressed air delivered to pneumatic components like rodless cylinders.
Moisture Content: Higher compression ratios generate more condensate, requiring enhanced air treatment systems and increasing the risk of moisture-related problems in pneumatic components.
Contamination Levels: Excessive heat from high compression ratios can cause oil carryover and contamination, particularly problematic for precision pneumatic applications.
Temperature Effects: Hot compressed air from high-ratio compression can cause thermal expansion in pneumatic cylinders, affecting positioning accuracy and seal performance.
System Optimization Strategies
Implement these strategies to optimize compression ratio for maximum efficiency and reliability:
Pressure Optimization: Operate at the lowest practical system pressure that meets application requirements. Reducing system pressure from 125 PSIG to 100 PSIG can improve efficiency by 12-15%.
Multi-Stage Implementation: Use multi-stage compression for high-pressure applications to maintain optimal stage ratios and improve overall efficiency.
Variable Speed Control: Implement variable speed drives to optimize compression ratios based on actual demand, reducing energy consumption during low-demand periods.
System Leak Reduction: Minimize system leaks to reduce compressor loading and allow operation at lower compression ratios.
Economic Analysis Methods
Quantify the economic impact of compression ratio optimization:
Energy Cost Calculation: Annual Energy Cost = Power (kW) × Operating Hours × Electricity Rate ($/kWh)
Life Cycle Cost Analysis: Include initial equipment cost, energy costs, maintenance costs, and replacement costs over the equipment life cycle.
Payback Period: Calculate payback period for compression ratio optimization projects: Payback = Initial Investment / Annual Savings
Return on Investment: ROI = (Annual Savings – Annual Cost) / Initial Investment × 100%
Case Study Examples
Manufacturing Plant Optimization: A Texas automotive parts manufacturer reduced their compression ratio from 11:1 to 8:1 by implementing two-stage compression, resulting in:
- 22% reduction in energy consumption
- $18,000 annual energy savings
- 60% reduction in maintenance costs
- Improved air quality for precision pneumatic applications
Food Processing Facility: A California food processor optimized their system pressure and compression ratio, achieving:
- 15% energy reduction
- Extended compressor life from 8 to 12 years
- Improved product quality through better air quality
- $25,000 annual cost savings
Monitoring and Control Systems
Implement monitoring systems to maintain optimal compression ratios:
Real-Time Monitoring: Track inlet and discharge pressures, temperatures, and energy consumption to identify optimization opportunities.
Automated Control: Use control systems to automatically adjust compression ratios based on demand patterns and efficiency optimization algorithms.
Performance Trending: Analyze long-term performance data to identify degradation trends and optimize maintenance schedules.
Michael, who manages facilities at a Pennsylvania packaging plant, shared his compression ratio optimization experience: “We were operating our compressors at 13:1 ratio and experiencing constant maintenance problems with our pneumatic systems, including frequent seal failures in our rodless cylinders. After working with Bepto to optimize our compression ratio to 8:1 through system redesign, we reduced our energy costs by $32,000 annually and extended our equipment life by an average of 40%. The improved air quality also eliminated the positioning problems we were having with our precision pneumatic applications.”
Conclusion
Proper compression ratio calculation and optimization is essential for efficient pneumatic system operation, with optimal ratios of 7:1-9:1 providing the best balance of energy efficiency, equipment reliability, and performance for rodless cylinders and other pneumatic components.
FAQs About Compressor Compression Ratio
Q: What’s the difference between using gauge pressure and absolute pressure in compression ratio calculations?
Absolute pressure includes atmospheric pressure (14.7 PSI at sea level) while gauge pressure does not; using gauge pressure gives incorrect ratios – for example, 100 PSIG system pressure gives a 7.8:1 ratio using absolute pressure (114.7/14.7) versus an impossible infinite ratio using gauge pressure (100/0).
Q: What happens if my compressor compression ratio is too high?
Excessive compression ratios (>12:1 single-stage) cause 50-70% reduction in equipment life, 30-50% higher energy consumption, excessive heat generation (discharge temperatures >450°F), and poor air quality that can damage pneumatic components like rodless cylinders through moisture and contamination.
Q: How do I determine the optimal compression ratio for my pneumatic system?
Calculate required system pressure including distribution losses, convert to absolute pressures, divide by inlet absolute pressure, then compare with compressor type limits: reciprocating (6:1-8:1), rotary screw (8:1-12:1), ensuring the ratio provides adequate pressure for your pneumatic applications while maintaining efficiency.
Q: Can I use multi-stage compression to achieve higher compression ratios efficiently?
Yes, multi-stage compression with intercooling allows efficient high-pressure operation by dividing total compression across stages (typically 3:1-4:1 per stage), reducing energy consumption by 15-30% and improving equipment life compared to single-stage high-ratio compression.
Q: How does altitude affect compressor compression ratio calculations?
Higher altitude reduces atmospheric pressure (12.2 PSIA at 5,000 feet vs. 14.7 PSIA at sea level), increasing compression ratios for the same gauge pressures – a 100 PSIG system has 7.8:1 ratio at sea level but 11.2:1 ratio at 5,000 feet, requiring larger compressors or multi-stage designs.
-
[Learn the critical difference between absolute and gauge pressure measurements in industrial systems] ↩
-
[Understand the thermodynamic principles governing air compression efficiency] ↩
-
[Discover how compressor design affects air delivery performance] ↩
-
[Explore the physics of compression heating and cooling requirements] ↩
-
[Learn how modern control systems optimize compressor energy consumption] ↩



