The physics behind vane-type rotary actuators involves complex interactions between fluid dynamics, mechanical forces, and thermodynamics that most engineers never fully understand. Yet mastering these principles is crucial for optimizing performance, predicting behavior, and solving application challenges that can make or break a project. 🔬
Vane-type rotary actuators operate on Pascal’s principle of pressure multiplication, converting linear pneumatic force into rotational torque through sliding vane mechanisms, with performance governed by pressure differentials, vane geometry, friction coefficients, and thermodynamic gas laws that determine torque output, speed, and efficiency characteristics.
I recently worked with a design engineer named Jennifer at an aerospace manufacturing facility in Seattle who was struggling with torque inconsistencies in her rotary actuator application. Her actuators were producing 30% less torque than calculated, causing positioning errors in critical assembly operations. The root cause wasn’t mechanical—it was a fundamental misunderstanding of the physics governing vane actuator behavior. ✈️
Table of Contents
- How Do Pressure Dynamics Generate Rotational Torque in Vane-Type Actuators?
- What Role Does Vane Geometry Play in Determining Actuator Performance Characteristics?
- Which Thermodynamic Principles Affect Rotary Actuator Speed and Efficiency?
- How Do Friction Forces and Mechanical Losses Impact Real-World Actuator Performance?
How Do Pressure Dynamics Generate Rotational Torque in Vane-Type Actuators?
Understanding pressure-to-torque conversion is fundamental to rotary actuator design and application.
Vane-type actuators generate torque through pressure differentials acting on vane surfaces, where torque equals pressure difference times effective vane area times moment arm1 distance, with the relationship T = ΔP × A × r, modified by vane angle and chamber geometry to create rotational motion from linear pneumatic forces.
Fundamental Torque Generation Principles
Pascal’s Principle Application
The foundation of rotary actuator operation lies in Pascal’s principle2:
- Pressure transmission: Uniform pressure acts on all surfaces within the chamber
- Force multiplication: Pressure × area = force on each vane surface
- Moment creation: Force × radius = torque about the central axis
Torque Calculation Fundamentals
Basic Torque Formula: T = ΔP × A_eff × r_eff × η
Where:
- T = Output torque (lb-in)
- ΔP = Pressure differential (PSI)
- A_eff = Effective vane area (sq in)
- r_eff = Effective moment arm (inches)
- η = Mechanical efficiency (0.85-0.95)
Pressure Distribution Analysis
Chamber Pressure Dynamics
The pressure distribution within vane chambers isn’t uniform:
- High-pressure chamber: Supply pressure minus flow losses
- Low-pressure chamber: Exhaust pressure plus back-pressure
- Transition zones: Pressure gradients at vane edges
- Dead volumes: Trapped air in clearance spaces
Effective Area Calculations
| Vane Configuration | Effective Area Formula | Efficiency Factor |
|---|---|---|
| Single Vane | A = L × W × sin(θ) | 0.85-0.90 |
| Double Vane | A = 2 × L × W × sin(θ/2) | 0.88-0.93 |
| Multi-Vane | A = n × L × W × sin(θ/n) | 0.90-0.95 |
Where L = vane length, W = vane width, θ = rotation angle, n = number of vanes
Dynamic Pressure Effects
Flow-Induced Pressure Losses
Real-world pressure dynamics include flow-related losses:
- Inlet restrictions: Valve and fitting pressure drops
- Internal flow losses: Turbulence and friction in chambers
- Exhaust restrictions: Back-pressure from exhaust systems
- Acceleration losses: Pressure required to accelerate moving air
Jennifer’s aerospace application suffered from inadequate supply line sizing that created a 15 PSI pressure drop during rapid actuator movements. This pressure loss, combined with dynamic flow effects, explained the 30% torque reduction she was experiencing. 📉
What Role Does Vane Geometry Play in Determining Actuator Performance Characteristics?
Vane geometry directly influences torque output, rotation angle, speed, and efficiency characteristics.
Vane geometry determines actuator performance through vane length (affects torque arm), width (determines pressure area), thickness (impacts sealing and friction), angle relationships (controls rotation range), and clearance specifications (affects leakage and efficiency), with each parameter requiring optimization for specific applications.
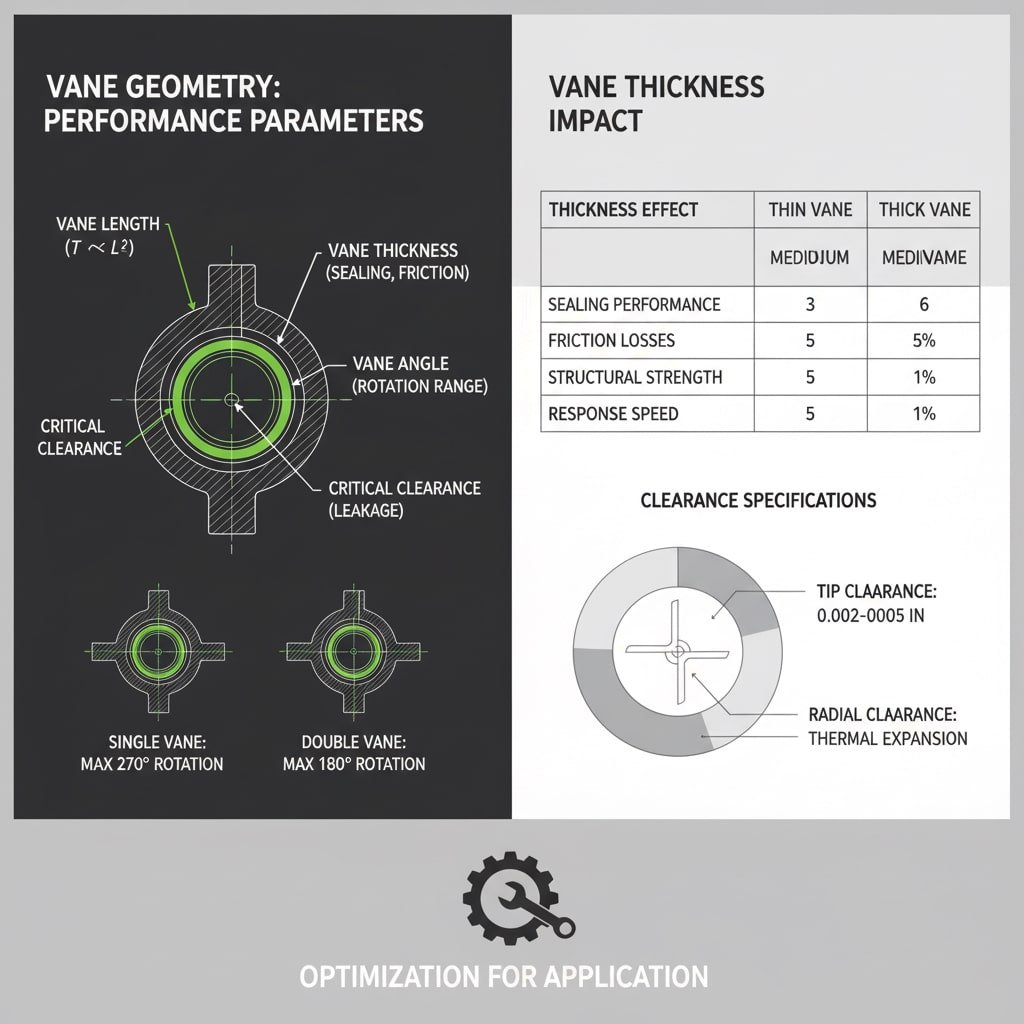
Geometric Parameter Analysis
Vane Length Optimization
Vane length directly affects torque output and structural integrity:
- Torque relationship: T ∝ L² (length squared relationship)
- Stress considerations: Bending stress increases with length cubed
- Deflection effects: Longer vanes experience more tip deflection
- Optimal ratios: Length-to-width ratios of 3:1 to 5:1 provide best performance
Vane Thickness Impact
Vane thickness affects multiple performance parameters:
| Thickness Effect | Thin Vanes (< 0.25″) | Medium Vanes (0.25″-0.5″) | Thick Vanes (> 0.5″) |
|---|---|---|---|
| Sealing Performance | Poor – high leakage | Good – adequate contact | Excellent – tight seals |
| Friction Losses | Low | Medium | High |
| Structural Strength | Poor – deflection issues | Good – adequate stiffness | Excellent – rigid |
| Response Speed | Fast | Medium | Slow |
Angular Geometry Considerations
Rotation Angle Limitations
Vane geometry constrains maximum rotation angles:
- Single vane: Maximum ~270° rotation
- Double vane: Maximum ~180° rotation
- Multi-vane: Rotation limited by vane interference
- Chamber design: Housing geometry affects usable angle
Vane Angle Optimization
The angle between vanes affects torque characteristics:
- Equal spacing: Provides smooth torque delivery
- Unequal spacing: Can optimize torque curves for specific applications
- Progressive angles: Compensate for pressure variations
Clearance and Sealing Geometry
Critical Clearance Specifications
Proper clearances balance sealing effectiveness with friction:
- Tip clearance: 0.002″-0.005″ for optimal sealing
- Side clearance: 0.001″-0.003″ to prevent binding
- Radial clearance: Temperature expansion considerations
- Axial clearance: Thrust bearing and thermal growth
At Bepto, our vane geometry optimization process uses computational fluid dynamics (CFD)3 analysis combined with empirical testing to achieve the ideal balance of torque, speed, and efficiency for each application. This engineering approach has enabled us to achieve 15-20% higher efficiency than standard designs. 🔧
Which Thermodynamic Principles Affect Rotary Actuator Speed and Efficiency?
Thermodynamic effects significantly impact actuator performance, especially in high-speed or high-duty applications.
Thermodynamic principles affecting rotary actuators include gas expansion and compression during rotation, heat generation from friction and pressure drops, temperature effects on air density and viscosity, and adiabatic versus isothermal processes that determine actual versus theoretical performance in real operating conditions.

Gas Law Applications
Ideal Gas Law Effects
Rotary actuator performance follows gas law relationships:
- Pressure-volume work: W = ∫P dV during expansion
- Temperature effects: PV = nRT governs pressure-temperature relationships
- Density variations: ρ = PM/RT affects mass flow calculations
- Compressibility: Real gas effects at high pressures
Adiabatic vs. Isothermal Processes
Actuator operation involves both process types:
| Process Type | Characteristics | Performance Impact |
|---|---|---|
| Adiabatic | No heat transfer, rapid expansion | Higher pressure drops, temperature changes |
| Isothermal | Constant temperature, slow expansion | More efficient energy conversion |
| Polytropic | Real-world combination | Actual performance between extremes |
Heat Generation and Transfer
Friction-Induced Heating
Multiple sources generate heat in rotary actuators:
- Vane tip friction: Sliding contact with housing
- Bearing friction: Shaft support bearing losses
- Seal friction: Rotary seal drag forces
- Fluid friction: Viscous losses in air flow
Temperature Rise Calculations
Heat generation rate: Q = μ × N × F × V
Where:
- Q = Heat generation (BTU/hr)
- μ = Coefficient of friction
- N = Rotational speed (RPM)
- F = Normal force (lbs)
- V = Sliding velocity (ft/min)
Efficiency Analysis
Thermodynamic Efficiency Factors
Overall efficiency combines multiple loss mechanisms:
- Volumetric efficiency: ηv = Actual flow / Theoretical flow
- Mechanical efficiency: ηm = Output power / Input power
- Overall efficiency: ηo = ηv × ηm
Efficiency Optimization Strategies
| Strategy | Efficiency Gain | Implementation Cost |
|---|---|---|
| Improved sealing | 5-15% | Medium |
| Optimized clearances | 3-8% | Low |
| Advanced materials | 8-12% | High |
| Thermal management | 5-10% | Medium |
Flow Dynamics and Pressure Losses
Reynolds Number Effects
Flow characteristics change with operating conditions:
- Laminar flow: Re < 2300, predictable pressure losses
- Turbulent flow: Re > 4000, higher friction factors
- Transition region: Unpredictable flow characteristics
The thermodynamic analysis revealed that Jennifer’s aerospace application was experiencing significant temperature rise during rapid cycling, which reduced air density by 12% and contributed to the torque loss. We implemented thermal management strategies that restored full performance. 🌡️
How Do Friction Forces and Mechanical Losses Impact Real-World Actuator Performance?
Friction and mechanical losses significantly reduce theoretical performance and must be carefully managed for optimal actuator operation.
Mechanical losses in vane-type actuators include sliding friction at vane tips, rotary seal drag, bearing friction, and internal air turbulence, typically reducing theoretical torque output by 10-20% and requiring careful material selection, surface treatments, and lubrication strategies to minimize performance degradation.
Friction Analysis and Modeling
Vane Tip Friction Mechanisms
The primary friction source occurs at vane-to-housing interfaces:
- Boundary lubrication: Direct metal-to-metal contact
- Mixed lubrication: Partial fluid film separation
- Hydrodynamic lubrication: Full fluid film (rare in pneumatics)
Friction Coefficient Variations
| Material Combination | Dry Friction (μ) | Lubricated Friction (μ) | Temperature Sensitivity |
|---|---|---|---|
| Steel on Steel | 0.6-0.8 | 0.1-0.15 | High |
| Steel on Bronze | 0.3-0.5 | 0.08-0.12 | Medium |
| Steel on PTFE | 0.1-0.2 | 0.05-0.08 | Low |
| Ceramic Coating | 0.2-0.3 | 0.06-0.10 | Very Low |
Bearing Loss Analysis
Radial Bearing Friction
Output shaft bearings contribute significant losses:
- Rolling friction: Fr = μr × N × r
- Sliding friction: Fs = μs × N
- Viscous friction: Fv = η × A × V/h
- Seal friction: Additional drag from shaft seals
Bearing Selection Impact
Different bearing types affect overall efficiency:
- Ball bearings: Low friction, high precision
- Roller bearings: Higher load capacity, moderate friction
- Plain bearings: High friction, simple construction
- Magnetic bearings: Near-zero friction, high cost
Surface Engineering Solutions
Advanced Surface Treatments
Modern surface treatments dramatically reduce friction:
- Hard chrome plating: Reduces wear, moderate friction reduction
- Ceramic coatings: Excellent wear resistance, low friction
- Diamond-like carbon (DLC): Ultra-low friction, expensive
- Specialized polymers: Application-specific solutions
Lubrication Strategies
| Lubrication Method | Friction Reduction | Maintenance Requirements | Cost Impact |
|---|---|---|---|
| Oil Mist Systems | 60-80% | High – regular replenishment | High |
| Solid Lubricants | 40-60% | Low – long service life | Medium |
| Self-Lubricating Materials | 50-70% | Very Low – permanent | High initial |
| Dry Film Lubricants | 30-50% | Medium – periodic reapplication | Low |
Performance Optimization Strategies
Integrated Design Approach
At Bepto, we optimize friction through systematic design:
- Material selection: Compatible material pairs
- Surface finish: Optimized roughness for each application
- Clearance control: Minimize contact pressure
- Thermal management: Control temperature-induced expansion
Real-World Performance Validation
Laboratory testing versus field performance often differs:
- Break-in effects: Performance improves with initial operation
- Contamination impact: Real-world dirt and debris effects
- Temperature cycling: Thermal expansion and contraction
- Load variations: Dynamic loading versus static test conditions
Our comprehensive friction analysis and optimization program helped Jennifer’s aerospace application achieve 95% of theoretical torque output—a significant improvement from the original 70%. The key was implementing a multi-faceted approach combining advanced materials, optimized geometry, and proper lubrication. 🎯
Predictive Friction Modeling
Mathematical Friction Models
Accurate friction prediction requires sophisticated modeling:
- Coulomb friction: F = μ × N (basic model)
- Stribeck curve: Friction variation with velocity
- Temperature effects: μ(T) relationships
- Wear progression: Friction changes over time
Conclusion
Understanding the fundamental physics of vane-type rotary actuators—from pressure dynamics and thermodynamics to friction mechanisms—enables engineers to optimize performance, predict behavior, and solve complex application challenges.
FAQs About Vane-Type Rotary Actuator Physics
Q: How does operating pressure affect the relationship between theoretical and actual torque output?
A: Higher operating pressures generally improve the theoretical-to-actual torque ratio because mechanical losses become a smaller percentage of total output. However, increased pressure also elevates friction forces, so the relationship isn’t linear. Optimal pressure depends on specific application requirements and actuator design.
Q: Why do rotary actuators lose torque at high speeds, and how can this be minimized?
A: High-speed torque loss occurs due to increased friction, flow restrictions, and thermodynamic effects. Minimize losses through optimized port sizing, advanced bearing systems, improved sealing designs, and thermal management. Flow velocity limitations become the primary constraint above certain speeds.
Q: How do temperature variations affect rotary actuator performance calculations?
A: Temperature affects air density (impacts force), viscosity (affects flow), material properties (changes friction), and thermal expansion (alters clearances). A 100°F temperature increase can reduce torque output by 15-25% through combined effects. Temperature compensation in control systems helps maintain consistent performance.
Q: What’s the relationship between vane tip speed and friction losses in rotary actuators?
A: Friction losses generally increase with the square of tip speed due to increased contact forces and heat generation. However, at very low speeds, static friction dominates, creating a complex relationship. Optimal operating speeds typically fall in the middle range where dynamic friction is manageable.
Q: How do you account for air compressibility effects in rotary actuator performance calculations?
A: Air compressibility becomes significant at pressures above 100 PSI and during rapid acceleration. Use compressible flow equations instead of incompressible assumptions, account for pressure wave propagation delays, and consider adiabatic expansion effects. Real gas properties may be needed for high-pressure applications above 200 PSI.
-
Learn the definition of a moment arm, the perpendicular distance from an axis of rotation to the line of action of a force, which is critical for calculating torque. ↩
-
Understand Pascal’s principle, the fundamental law of fluid mechanics that explains how pressure is transmitted in a confined fluid. ↩
-
Explore the field of Computational Fluid Dynamics (CFD), a branch of fluid mechanics that uses numerical analysis to solve and analyze problems involving fluid flows. ↩




