
Have you ever wondered why some pneumatic systems deliver inconsistent performance despite meeting all design specifications? Or why a system that works perfectly in your facility fails when installed at a customer’s high-altitude location? The answer often lies in the misunderstood world of gas dynamics.
Gas dynamics is the study of gas flow behavior under varying conditions of pressure, temperature, and velocity. In pneumatic systems, understanding gas dynamics is crucial because flow characteristics change dramatically as gas velocity approaches and exceeds the speed of sound, creating phenomena like choked flow1, shock waves2, and expansion fans that significantly impact system performance.
Last year, I consulted for a medical device manufacturer in Colorado whose precision pneumatic positioning system worked flawlessly during development but failed quality testing in production. Their engineers were baffled by the inconsistent performance. By analyzing the gas dynamics—particularly the formation of shock waves in their valve system—we identified that they were operating in a transonic flow regime that created unpredictable force output. A simple redesign of the flow path eliminated the issue and saved them months of trial-and-error troubleshooting. Let me show you how understanding gas dynamics can transform your pneumatic system performance.
Table of Contents
- Mach Number Impact: How Does Gas Velocity Affect Your Pneumatic System?
- Shock Wave Formation: What Conditions Create These Performance-Killing Discontinuities?
- Compressible Flow Equations: Which Mathematical Models Drive Accurate Pneumatic Design?
- Conclusion
- FAQs About Gas Dynamics in Pneumatic Systems
Mach Number Impact: How Does Gas Velocity Affect Your Pneumatic System?
The Mach number3—the ratio of flow velocity to the local speed of sound—is the most critical parameter in gas dynamics. Understanding how different Mach number regimes affect pneumatic system behavior is essential for reliable design and troubleshooting.
The Mach number (M) dramatically influences pneumatic flow behavior, with distinct regimes: subsonic (M<0.8) where flow is predictable and follows traditional models, transonic (0.8<M<1.2) where mixed flow behaviors create instabilities, supersonic (M>1.2) where shock waves form, and choked flow (M=1 at restrictions) where flow rate becomes independent of downstream conditions regardless of pressure differential.
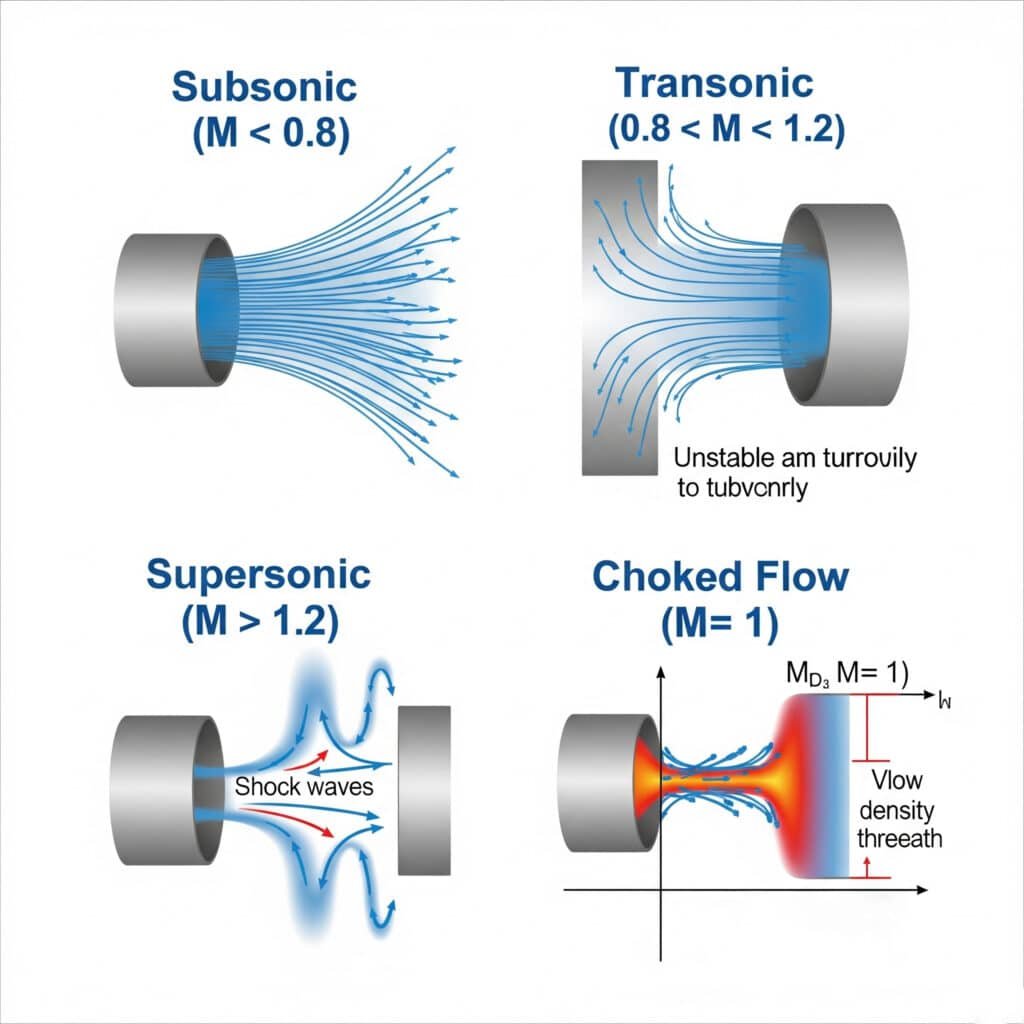
I remember troubleshooting a packaging machine in Wisconsin that experienced erratic cylinder performance despite using “properly sized” components. The system worked perfectly at low speeds but became unpredictable during high-speed operation. When we analyzed the valve-to-cylinder tubing, we discovered flow velocities reaching Mach 0.9 during rapid cycling—placing the system in the problematic transonic regime. By increasing the supply line diameter by just 2mm, we reduced the Mach number to 0.65 and completely eliminated the performance issues.
Mach Number Definition and Significance
The Mach number is defined as:
M = V/c
Where:
- M = Mach number (dimensionless)
- V = Flow velocity (m/s)
- c = Local speed of sound (m/s)
For air at typical conditions, the speed of sound is approximately:
c = √(γRT)
Where:
- γ = Specific heat ratio (1.4 for air)
- R = Specific gas constant (287 J/kg·K for air)
- T = Absolute temperature (K)
At 20°C (293K), the speed of sound in air is approximately 343 m/s.
Flow Regimes and Their Characteristics
| Mach Number Range | Flow Regime | Key Characteristics | System Implications |
|---|---|---|---|
| M < 0.3 | Incompressible | Density changes negligible | Traditional hydraulic equations apply |
| 0.3 < M < 0.8 | Subsonic Compressible | Moderate density changes | Compressibility corrections needed |
| 0.8 < M < 1.2 | Transonic | Mixed subsonic/supersonic regions | Flow instabilities, noise, vibration |
| M > 1.2 | Supersonic | Shock waves, expansion fans | Pressure recovery issues, high losses |
| M = 1 (at restrictions) | Choked Flow | Maximum mass flow rate reached | Flow independent of downstream pressure |
Practical Mach Number Calculation
For a pneumatic system with:
- Supply pressure (p₁): 6 bar (absolute)
- Downstream pressure (p₂): 1 bar (absolute)
- Pipe diameter (D): 8mm
- Flow rate (Q): 500 standard liters per minute (SLPM)
The Mach number can be calculated as:
- Convert flow rate to mass flow: ṁ = ρ₀ × Q = 1.2 kg/m³ × (500/60000) m³/s = 0.01 kg/s
- Calculate density at operating pressure: ρ = ρ₀ × (p₁/p₀) = 1.2 × (6/1) = 7.2 kg/m³
- Calculate flow area: A = π × (D/2)² = π × (0.004)² = 5.03 × 10⁻⁵ m²
- Calculate velocity: V = ṁ/(ρ × A) = 0.01/(7.2 × 5.03 × 10⁻⁵) = 27.7 m/s
- Calculate Mach number: M = V/c = 27.7/343 = 0.08
This low Mach number indicates incompressible flow behavior in this particular example.
Critical Pressure Ratio and Choked Flow
One of the most important concepts in pneumatic system design is the critical pressure ratio that causes choked flow:
(p₂/p₁)critical = (2/(γ+1))^(γ/(γ-1))
For air (γ = 1.4), this equals approximately 0.528.
When the ratio of downstream to upstream absolute pressure falls below this critical value, flow becomes choked at restrictions, with significant implications:
- Flow Limitation: Mass flow rate cannot increase regardless of further downstream pressure reduction
- Sonic Condition: Flow velocity reaches exactly Mach 1 at the restriction
- Downstream Independence: Conditions downstream of the restriction cannot affect upstream flow
- Maximum Flow Rate: The system reaches its maximum possible flow rate
Mach Number Effects on System Parameters
| Parameter | Low Mach Number Effect | High Mach Number Effect |
|---|---|---|
| Pressure Drop | Proportional to velocity squared | Non-linear, exponential increase |
| Temperature | Minimal changes | Significant cooling during expansion |
| Density | Nearly constant | Varies significantly throughout system |
| Flow Rate | Linear with pressure differential | Limited by choking conditions |
| Noise Generation | Minimal | Significant, especially in transonic range |
| Control Responsiveness | Predictable | Potentially unstable near M=1 |
Case Study: Rodless Cylinder Performance Across Mach Regimes
For a high-speed rodless cylinder application:
| Parameter | Low-Speed Operation (M=0.15) | High-Speed Operation (M=0.85) | Impact |
|---|---|---|---|
| Cycle Time | 1.2 seconds | 0.3 seconds | 4× faster |
| Flow Velocity | 51 m/s | 291 m/s | 5.7× higher |
| Pressure Drop | 0.2 bar | 1.8 bar | 9× higher |
| Force Output | 650 N | 480 N | 26% reduction |
| Positioning Accuracy | ±0.5mm | ±2.1mm | 4.2× worse |
| Energy Consumption | 0.4 Nl/cycle | 1.1 Nl/cycle | 2.75× higher |
This case study demonstrates how high Mach number operation dramatically affects system performance across multiple parameters.
Shock Wave Formation: What Conditions Create These Performance-Killing Discontinuities?
Shock waves are one of the most disruptive phenomena in pneumatic systems, creating sudden pressure changes, energy losses, and flow instabilities. Understanding the conditions that create shock waves is essential for reliable high-performance pneumatic design.
Shock waves form when flow transitions from supersonic to subsonic velocity, creating a near-instantaneous discontinuity where pressure increases, temperature rises, and entropy grows. In pneumatic systems, shock waves commonly occur in valves, fittings, and diameter changes when the pressure ratio exceeds the critical value of approximately 1.89:1, resulting in energy losses of 10-30% and potential system instabilities.
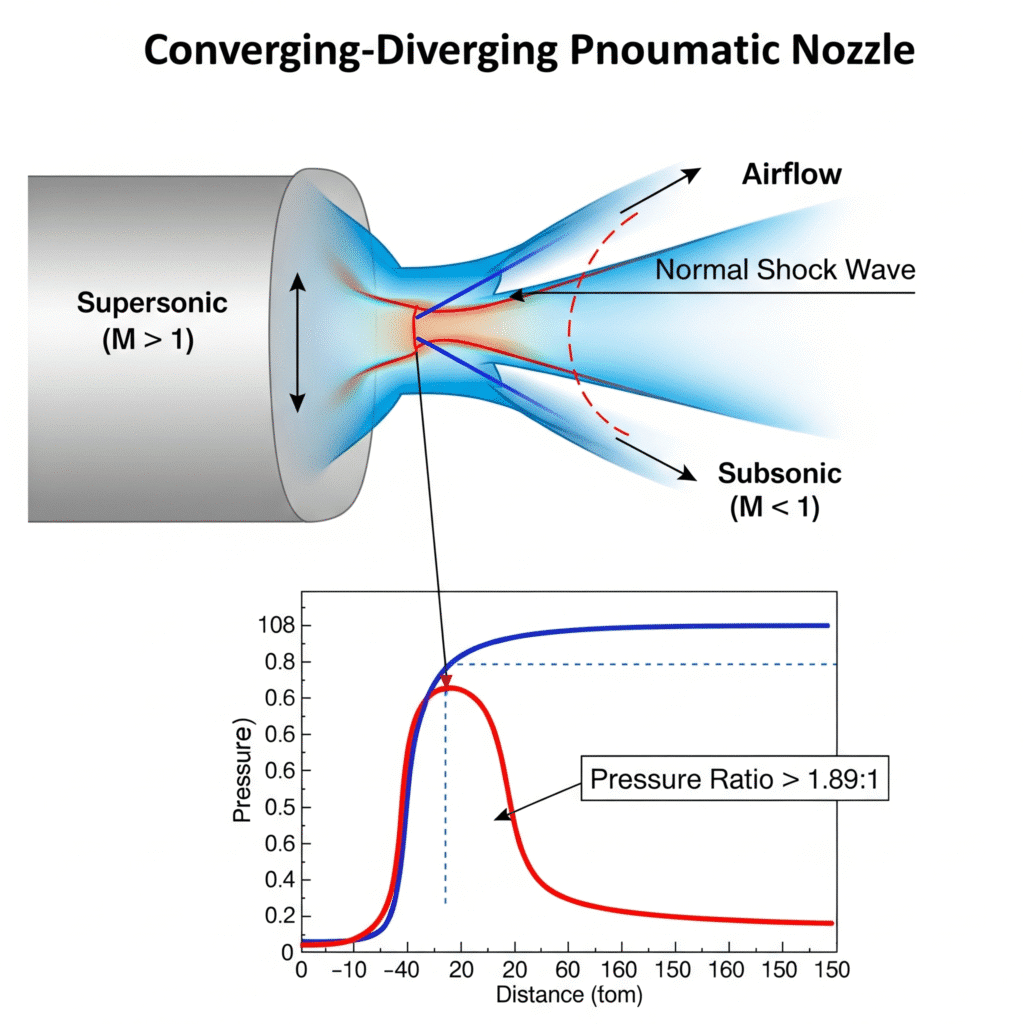
During a recent consultation with an automotive testing equipment manufacturer in Michigan, their engineers were puzzled by the inconsistent force output and excessive noise in their high-speed pneumatic impact tester. Our analysis revealed multiple oblique shock waves forming in their valve body during operation. By redesigning the internal flow path to create a more gradual expansion, we eliminated the shock formations, reduced noise by 14 dBA, and improved force consistency by 320%—turning an unreliable prototype into a marketable product.
Fundamental Shock Wave Physics
A shock wave represents a discontinuity in the flow field where properties change almost instantaneously across a very thin region:
| Property | Change Across Normal Shock |
|---|---|
| Velocity | Supersonic → Subsonic |
| Pressure | Sudden increase |
| Temperature | Sudden increase |
| Density | Sudden increase |
| Entropy | Increases (irreversible process) |
| Mach Number | M₁ > 1 → M₂ < 1 |
Types of Shock Waves in Pneumatic Systems
Different system geometries create different shock structures:
Normal Shocks
Perpendicular to flow direction:
- Occur in straight sections when supersonic flow must transition to subsonic
- Maximum entropy increase and energy loss
- Commonly found in valve outlets and tube entrances
Oblique Shocks
Angled relative to flow direction:
- Form at corners, bends, and flow obstructions
- Less severe pressure rise than normal shocks
- Create asymmetric flow patterns and side forces
Expansion Fans
Not true shocks, but related phenomena:
- Occur when supersonic flow turns away from itself
- Create gradual pressure decrease and cooling
- Often interact with shock waves in complex geometries
Mathematical Conditions for Shock Formation
For a normal shock wave, the relationship between upstream (1) and downstream (2) conditions can be expressed through the Rankine-Hugoniot equations:
Pressure ratio:
p₂/p₁ = (2γM₁² – (γ-1))/(γ+1)
Temperature ratio:
T₂/T₁ = [2γM₁² – (γ-1)][(γ-1)M₁² + 2]/[(γ+1)²M₁²]
Density ratio:
ρ₂/ρ₁ = (γ+1)M₁²/[(γ-1)M₁² + 2]
Downstream Mach number:
M₂² = [(γ-1)M₁² + 2]/[2γM₁² – (γ-1)]
Critical Pressure Ratios for Shock Formation
For air (γ = 1.4), important threshold values include:
| Pressure Ratio (p₂/p₁) | Significance | System Implication |
|---|---|---|
| < 0.528 | Choked flow condition | Maximum flow rate reached |
| 0.528 – 1.0 | Underexpanded flow | Expansion occurs outside restriction |
| 1.0 | Perfectly expanded | Ideal expansion (rare in practice) |
| > 1.0 | Overexpanded flow | Shock waves form to match back pressure |
| > 1.89 | Normal shock formation | Significant energy loss occurs |
Shock Wave Detection and Diagnosis
Identifying shock waves in operational systems:
Acoustic Signatures
– Sharp cracking or hissing sounds
– Broadband noise with tonal components
– Frequency analysis showing peaks at 2-8 kHzPressure Measurements
– Sudden pressure discontinuities
– Pressure fluctuations and instabilities
– Non-linear pressure-flow relationshipsThermal Indicators
– Localized heating at shock locations
– Temperature gradients in flow path
– Thermal imaging revealing hot spotsFlow Visualization (for transparent components)
– Schlieren imaging showing density gradients
– Particle tracking revealing flow disturbances
– Condensation patterns indicating pressure changes
Practical Shock Wave Mitigation Strategies
Based on my experience with industrial pneumatic systems, here are the most effective approaches for preventing or minimizing shock wave formation:
Geometric Modifications
Gradual Expansion Paths
– Use conical diffusers with 5-15° included angles
– Implement multiple small steps instead of single large changes
– Avoid sharp corners and sudden expansionsFlow Straighteners
– Add honeycomb or mesh structures before expansions
– Use guide vanes in bends and turns
– Implement flow conditioning chambers
Operational Adjustments
Pressure Ratio Management
– Maintain ratios below critical values where possible
– Use multi-stage pressure reduction for large drops
– Implement active pressure control for varying conditionsTemperature Control
– Pre-heat gas for critical applications
– Monitor temperature drops across expansions
– Compensate for temperature effects on downstream components
Case Study: Valve Redesign to Eliminate Shock Waves
For a high-flow directional control valve exhibiting shock-related issues:
| Parameter | Original Design | Shock-Optimized Design | Improvement |
|---|---|---|---|
| Flow Path | 90° turns, sudden expansions | Gradual turns, staged expansion | Eliminated normal shock |
| Pressure Drop | 1.8 bar at 1500 SLPM | 0.7 bar at 1500 SLPM | 61% reduction |
| Noise Level | 94 dBA | 81 dBA | 13 dBA reduction |
| Flow Coefficient (Cv) | 1.2 | 2.8 | 133% increase |
| Response Consistency | ±12ms variation | ±3ms variation | 75% improvement |
| Energy Efficiency | 68% | 89% | 21% improvement |
Compressible Flow Equations: Which Mathematical Models Drive Accurate Pneumatic Design?
Accurate mathematical modeling of compressible flow is essential for pneumatic system design, optimization, and troubleshooting. Understanding which equations apply under different conditions allows engineers to predict system behavior and avoid costly design errors.
Compressible flow in pneumatic systems is governed by conservation equations for mass, momentum, and energy, coupled with the equation of state. These equations change form depending on the Mach regime: for subsonic flow (M<0.3), simplified Bernoulli equations often suffice; for moderate speeds (0.3<M<0.8), compressible Bernoulli with density corrections applies; and for high-speed flows (M>0.8), full compressible flow equations with shock relations become necessary.

I recently worked with a semiconductor equipment manufacturer in Oregon whose pneumatic positioning system exhibited mysterious force variations that their simulations couldn’t predict. Their engineers had used incompressible flow equations in their models, missing critical compressible effects. By implementing proper gas dynamic equations and accounting for local Mach numbers, we created a model that accurately predicted system behavior across all operating conditions. This allowed them to optimize their design and achieve the ±0.01mm positioning accuracy their process required.
Fundamental Conservation Equations
The behavior of compressible gas flow is governed by three fundamental conservation principles:
Conservation of Mass (Continuity Equation)
For steady one-dimensional flow:
ρ₁A₁V₁ = ρ₂A₂V₂ = ṁ (constant)
Where:
- ρ = Density (kg/m³)
- A = Cross-sectional area (m²)
- V = Velocity (m/s)
- ṁ = Mass flow rate (kg/s)
Conservation of Momentum
For a control volume with no external forces except pressure:
p₁A₁ + ρ₁A₁V₁² = p₂A₂ + ρ₂A₂V₂²
Where:
- p = Pressure (Pa)
Conservation of Energy
For adiabatic flow with no work or heat transfer:
h₁ + V₁²/2 = h₂ + V₂²/2
Where:
- h = Specific enthalpy (J/kg)
For a perfect gas with constant specific heats:
c_pT₁ + V₁²/2 = c_pT₂ + V₂²/2
Where:
- c_p = Specific heat at constant pressure (J/kg·K)
- T = Temperature (K)
Equation of State
For ideal gases:
p = ρRT
Where:
- R = Specific gas constant (J/kg·K)
Isentropic Flow Relations
For reversible, adiabatic (isentropic) processes, several useful relations can be derived:
Pressure-density relation:
p/ρᵞ = constant
Temperature-pressure relation:
T/p^((γ-1)/γ) = constant
These lead to the isentropic flow equations relating conditions at any two points:
p₂/p₁ = (T₂/T₁)^(γ/(γ-1)) = (ρ₂/ρ₁)^γ
Mach Number Relations for Isentropic Flow
For isentropic flow, several critical relationships involve the Mach number:
Temperature ratio:
T₀/T = 1 + ((γ-1)/2)M²
Pressure ratio:
p₀/p = [1 + ((γ-1)/2)M²]^(γ/(γ-1))
Density ratio:
ρ₀/ρ = [1 + ((γ-1)/2)M²]^(1/(γ-1))
Where subscript 0 indicates stagnation (total) conditions.
Flow Through Variable Area Passages
For isentropic flow through varying cross-sections:
A/A* = (1/M)[2/(γ+1)(1+((γ-1)/2)M²)]^((γ+1)/(2(γ-1)))
Where A* is the critical area where M=1.
Mass Flow Rate Equations
For subsonic flow through restrictions:
ṁ = CdA₁p₁√(2γ/(γ-1)RT₁[(p₂/p₁)^(2/γ)-(p₂/p₁)^((γ+1)/γ)])
For choked flow (when p₂/p₁ ≤ (2/(γ+1))^(γ/(γ-1))):
ṁ = CdA₁p₁√(γ/RT₁)(2/(γ+1))^((γ+1)/(2(γ-1)))
Where Cd is the discharge coefficient accounting for non-ideal effects.
Non-Isentropic Flow: Fanno and Rayleigh Flow
Real pneumatic systems involve friction and heat transfer, requiring additional models:
Fanno Flow (Adiabatic Flow with Friction)
Describes flow in constant area ducts with friction:
- Maximum entropy occurs at M=1
- Subsonic flow accelerates toward M=1 with increasing friction
- Supersonic flow decelerates toward M=1 with increasing friction
Key equation:
4fL/D = (1-M²)/(γM²) + ((γ+1)/(2γ))ln[(γ+1)M²/(2+(γ-1)M²)]
Where:
- f = Friction factor
- L = Duct length
- D = Hydraulic diameter
Rayleigh Flow (Frictionless Flow with Heat Transfer)
Describes flow in constant area ducts with heat addition/removal:
- Maximum entropy occurs at M=1
- Heat addition drives subsonic flow toward M=1 and supersonic flow away from M=1
- Heat removal has opposite effect
Practical Application of Compressible Flow Equations
Selecting the appropriate equations for different pneumatic applications:
| Application | Appropriate Model | Key Equations | Accuracy Considerations |
|---|---|---|---|
| Low-speed flow (M<0.3) | Incompressible | Bernoulli equation | Within 5% for M<0.3 |
| Medium-speed flow (0.3<M<0.8) | Compressible Bernoulli | Bernoulli with density corrections | Account for density changes |
| High-speed flow (M>0.8) | Full compressible | Isentropic relations, shock equations | Consider entropy changes |
| Flow restrictions | Orifice flow | Choked flow equations | Use appropriate discharge coefficients |
| Long pipelines | Fanno flow4 | Friction-modified gas dynamics | Include wall roughness effects |
| Temperature-sensitive applications | Rayleigh flow | Heat transfer-modified gas dynamics | Consider non-adiabatic effects |
Case Study: Precision Pneumatic Positioning System
For a semiconductor wafer handling system using rodless pneumatic cylinders:
| Parameter | Incompressible Model Prediction | Compressible Model Prediction | Actual Measured Value |
|---|---|---|---|
| Cylinder Velocity | 0.85 m/s | 0.72 m/s | 0.70 m/s |
| Acceleration Time | 18 ms | 24 ms | 26 ms |
| Deceleration Time | 22 ms | 31 ms | 33 ms |
| Positioning Accuracy | ±0.04 mm | ±0.012 mm | ±0.015 mm |
| Pressure Drop | 0.8 bar | 1.3 bar | 1.4 bar |
| Flow Rate | 95 SLPM | 78 SLPM | 75 SLPM |
This case study demonstrates how compressible flow models provide significantly more accurate predictions than incompressible models for pneumatic system design.
Computational Approaches for Complex Systems
For systems too complex for analytical solutions:
Method of Characteristics
– Solves hyperbolic partial differential equations
– Particularly useful for transient and wave propagation analysis
– Handles complex geometries with reasonable computational effortComputational Fluid Dynamics (CFD)5
– Finite volume/element methods for full 3D simulation
– Captures complex shock interactions and boundary layers
– Requires significant computational resources but provides detailed insightsReduced-Order Models
– Simplified representations based on fundamental equations
– Balance between accuracy and computational efficiency
– Particularly useful for system-level design and optimization
Conclusion
Understanding gas dynamics fundamentals—Mach number impacts, shock wave formation conditions, and compressible flow equations—provides the foundation for effective pneumatic system design, optimization, and troubleshooting. By applying these principles, you can create pneumatic systems that deliver consistent performance, higher efficiency, and greater reliability across a wide range of operating conditions.
FAQs About Gas Dynamics in Pneumatic Systems
At what point should I start considering compressible flow effects in my pneumatic system?
Compressibility effects become significant when flow velocities exceed Mach 0.3 (approximately 100 m/s for air at standard conditions). As a practical guideline, if your system operates with pressure ratios greater than 1.5:1 across components, or if flow rates exceed 300 SLPM through standard pneumatic tubing (8mm OD), compressible effects are likely significant. High-speed cycling, rapid valve switching, and long transmission lines also increase the importance of compressible flow analysis.
How do shock waves affect the reliability and lifespan of pneumatic components?
Shock waves create several detrimental effects that reduce component lifespan: they generate high-frequency pressure pulsations (500-5000 Hz) that accelerate seal and gasket fatigue; they create localized heating that degrades lubricants and polymer components; they increase mechanical vibration that loosens fittings and connections; and they cause flow instabilities that lead to inconsistent performance. Systems operating with frequent shock formation typically experience 40-60% shorter component life compared to shock-free designs.
What’s the relationship between the speed of sound and pneumatic system response time?
The speed of sound establishes the fundamental limit for pressure signal propagation in pneumatic systems—approximately 343 m/s in air at standard conditions. This creates a minimum theoretical response time of 2.9 milliseconds per meter of tubing. In practice, signal propagation is further slowed by restrictions, volume changes, and non-ideal gas behavior. For high-speed applications requiring response times below 20ms, keeping transmission lines under 2-3 meters and minimizing volume changes becomes critical to performance.
How do altitude and ambient conditions affect gas dynamics in pneumatic systems?
Altitude significantly impacts gas dynamics through reduced atmospheric pressure and typically lower temperatures. At 2000m elevation, atmospheric pressure is about 80% of sea level, reducing absolute pressure ratios across the system. The speed of sound decreases with lower temperatures (approximately 0.6 m/s per °C), affecting Mach number relationships. Systems designed for sea-level operation may experience significantly different behavior at altitude—including shifted critical pressure ratios, altered shock formation conditions, and changed choked flow thresholds.
What’s the most common gas dynamics mistake in pneumatic system design?
The most common mistake is undersizing flow passages based on incompressible flow assumptions. Engineers often select valve ports, fittings, and tubing using simple flow coefficient (Cv) calculations that ignore compressibility effects. This leads to unexpected pressure drops, flow limitations, and transonic flow regimes during operation. A related mistake is failing to account for the significant cooling that occurs during gas expansion—temperatures can drop 20-40°C during pressure reduction from 6 bar to atmospheric, affecting downstream component performance and causing condensation issues in humid environments.
-
Provides a fundamental explanation of the choked flow phenomenon, where the mass flow rate becomes independent of downstream pressure, a critical concept in designing pneumatic valves and orifices. ↩
-
Offers a detailed look at the physical conditions that lead to the formation of shock waves, including supersonic flow and pressure discontinuities, and their impact on fluid properties. ↩
-
Explains how the Mach number is calculated and how it defines the different regimes of compressible flow (subsonic, transonic, supersonic), which is essential for predicting system behavior. ↩
-
Describes the Fanno flow model, which is used to analyze steady, one-dimensional, adiabatic flow through a constant-area duct with friction, a common scenario in pneumatic pipelines. ↩
-
Provides an overview of Computational Fluid Dynamics (CFD), a powerful simulation tool used by engineers to analyze and visualize complex gas flow behavior that cannot be solved by simple equations. ↩


