
Have you ever touched a pneumatic cylinder after continuous operation and been surprised by how hot it feels? That heat isn’t just an inconvenience—it represents wasted energy, reduced efficiency, and potential reliability issues that could be costing your operation thousands.
Heat transfer in pneumatic systems occurs through three mechanisms: conduction through component materials, convection between surfaces and air, and radiation from hot surfaces. Understanding and optimizing these principles can reduce operating temperatures by 15-30%, extend component life by up to 40%, and improve energy efficiency by 5-15%.
Last month, I consulted for a food processing plant in Georgia where their rodless cylinders were failing every 3-4 months due to thermal issues. Their maintenance team was simply replacing components without addressing the root cause. By applying proper heat transfer principles, we reduced operating temperatures by 22°C and extended component life to over a year. Let me show you how we did it—and how you can apply these same principles to your systems.
Table of Contents
- Conduction Coefficient Calculation: How Does Heat Move Through Your Components?
- Convection Enhancement Methods: What Techniques Maximize Air-to-Surface Heat Transfer?
- Radiation Efficiency Model: When Does Thermal Radiation Matter in Pneumatic Systems?
- Conclusion
- FAQs About Heat Transfer in Pneumatic Systems
Conduction Coefficient Calculation: How Does Heat Move Through Your Components?
Conduction is the primary heat transfer mechanism within solid pneumatic components. Understanding how to calculate and optimize conduction coefficients is essential for managing system temperatures.
The heat conduction coefficient can be calculated using Fourier’s Law1: q = -k(dT/dx), where q is heat flux (W/m²), k is the thermal conductivity (W/m·K), and dT/dx is the temperature gradient. For pneumatic components, effective conduction depends on material selection, interface quality, and geometric factors that affect heat path length and cross-sectional area.
I remember troubleshooting a manufacturing line in Tennessee where the rodless cylinder bearings were failing prematurely. The maintenance team had tried multiple lubricants without success. When we analyzed the conduction paths, we discovered a thermal bottleneck at the bearing-housing interface. By improving the surface finish and applying a thermally conductive compound, we increased the effective conduction coefficient by 340% and eliminated the failures completely.
Fundamental Conduction Equations
Let’s break down the key equations for calculating conduction in pneumatic components:
Fourier’s Law for Heat Conduction
The basic equation governing heat conduction is:
q = -k(dT/dx)
Where:
- q = Heat flux (W/m²)
- k = Thermal conductivity (W/m·K)
- dT/dx = Temperature gradient (K/m)
For a simple one-dimensional case with constant cross-section:
Q = kA(T₁-T₂)/L
Where:
- Q = Heat transfer rate (W)
- A = Cross-sectional area (m²)
- T₁, T₂ = Temperatures at each end (K)
- L = Length of heat path (m)
Thermal Resistance Concept
For complex geometries, the thermal resistance approach is often more practical:
R = L/(kA)
Where:
- R = Thermal resistance (K/W)
For systems with multiple components in series:
Rtotal = R₁ + R₂ + R₃ + … + Rₙ
And the heat transfer rate becomes:
Q = ΔT/Rtotal
Material Thermal Conductivity Comparison
| Material | Thermal Conductivity (W/m·K) | Relative Conductivity | Common Applications |
|---|---|---|---|
| Aluminum | 205-250 | High | Cylinders, heat sinks |
| Steel | 36-54 | Medium | Structural components |
| Stainless Steel | 14-16 | Low-Medium | Corrosive environments |
| Bronze | 26-50 | Medium | Bearings, bushings |
| PTFE | 0.25 | Very Low | Seals, bearings |
| Nitrile Rubber | 0.13 | Very Low | O-rings, seals |
| Air (still) | 0.026 | Extremely Low | Gap filler |
| Thermal Paste | 3-8 | Low | Interface material |
Contact Resistance in Pneumatic Assemblies
At interfaces between components, contact resistance significantly affects heat transfer:
Rcontact = 1/(hc × A)
Where:
- hc = Contact coefficient (W/m²·K)
- A = Contact area (m²)
Factors affecting contact resistance include:
- Surface Roughness: Rougher surfaces have less actual contact area
- Contact Pressure: Higher pressure increases effective contact area
- Interface Materials: Thermal compounds fill air gaps
- Surface Cleanliness: Contaminants can increase resistance
Case Study: Rodless Cylinder Thermal Optimization
For a magnetic rodless cylinder experiencing thermal issues:
| Component | Original Design | Optimized Design | Improvement |
|---|---|---|---|
| Cylinder Body | Anodized Aluminum | Same material, improved finish | 15% better conduction |
| Bearing Interface | Metal-to-metal contact | Added thermal compound | 340% better conduction |
| Mounting Brackets | Painted steel | Bare aluminum | 280% better conduction |
| Overall Thermal Resistance | 2.8 K/W | 0.7 K/W | 75% reduction |
| Operating Temperature | 78°C | 56°C | 22°C reduction |
| Component Life | 4 months | >12 months | 3× improvement |
Practical Conduction Optimization Techniques
Based on my experience with hundreds of pneumatic systems, here are the most effective approaches for improving conduction:
Interface Optimization
- Surface Finishing: Improve mating surface smoothness to Ra 0.4-0.8 μm
- Thermal Interface Materials2: Apply appropriate compounds (3-8 W/m·K)
- Fastener Torque: Ensure proper tightening for optimal contact pressure
- Cleanliness: Remove all oils and contaminants before assembly
Material Selection Strategies
- Critical Heat Paths: Use high-conductivity materials (aluminum, copper)
- Thermal Breaks: Intentionally use low-conductivity materials to isolate heat
- Composite Approaches: Combine materials for optimal performance/cost
- Anisotropic Materials: Utilize directional conductivity where appropriate
Geometric Optimization
- Heat Path Length: Minimize distance between heat sources and sinks
- Cross-Sectional Area: Maximize area perpendicular to heat flow
- Thermal Bottlenecks: Identify and eliminate constrictions in heat path
- Redundant Paths: Create multiple parallel conduction routes
Convection Enhancement Methods: What Techniques Maximize Air-to-Surface Heat Transfer?
Convection is often the limiting factor in pneumatic system cooling. Enhancing convective heat transfer can dramatically improve thermal management and system performance.
Convective heat transfer follows Newton’s Law of Cooling3: Q = hA(Ts-T∞), where h is the convection coefficient (W/m²·K), A is the surface area, and (Ts-T∞) is the temperature difference between the surface and fluid. Enhancement methods include increasing surface area through fins, improving fluid velocity with directed airflow, and optimizing surface characteristics to promote turbulent boundary layers.
During an energy efficiency audit at a packaging facility in Arizona, I encountered a pneumatic system operating in a 43°C ambient environment. Their rodless cylinders were overheating despite meeting all maintenance requirements. By implementing targeted convection enhancement—adding small aluminum fins and a low-power fan—we increased the convection coefficient by 450%. This reduced operating temperatures from dangerous levels to within specification without any major system modifications.
Convection Heat Transfer Fundamentals
The basic equation governing convective heat transfer is:
Q = hA(Ts-T∞)
Where:
- Q = Heat transfer rate (W)
- h = Convection coefficient (W/m²·K)
- A = Surface area (m²)
- Ts = Surface temperature (K)
- T∞ = Fluid (air) temperature (K)
The convection coefficient h depends on multiple factors:
- Fluid properties (density, viscosity, thermal conductivity)
- Flow characteristics (velocity, turbulence)
- Surface geometry and orientation
- Flow regime (natural vs. forced convection)
Natural vs. Forced Convection
| Parameter | Natural Convection | Forced Convection | Implications |
|---|---|---|---|
| Typical h Value | 5-25 W/m²·K | 25-250 W/m²·K | Forced convection can be 10× more effective |
| Driving Force | Buoyancy (temperature difference) | External pressure (fans, blowers) | Forced convection is less dependent on temperature |
| Flow Pattern | Vertical flow along surfaces | Directional based on forcing mechanism | Forced flow can be optimized for specific components |
| Reliability | Passive, always present | Requires power and maintenance | Natural convection provides baseline cooling |
| Space Requirements | Requires clearance for air circulation | Requires space for air movers and ducting | Forced systems need more planning |
Convection Enhancement Techniques
Surface Area Augmentation
Increasing effective surface area through:
Fins and Extended Surfaces
– Pin fins: Omnidirectional airflow, 150-300% area increase
– Plate fins: Directional airflow, 200-500% area increase
– Corrugated surfaces: Moderate enhancement, 50-150% area increaseSurface Roughening
– Micro-texturing: 5-15% effective area increase
– Dimpled surfaces: 10-30% increase plus boundary layer effects
– Grooved patterns: 15-40% increase with directional benefits
Flow Manipulation
Improving airflow characteristics through:
Forced Air Systems
– Fans: Directional airflow, 200-600% h improvement
– Blowers: High-pressure flow, 300-800% h improvement
– Compressed air jets: Targeted cooling, 400-1000% local h improvementFlow Path Optimization
– Baffles: Direct air to critical components
– Venturi effects: Accelerate air over specific surfaces
– Vortex generators: Create turbulence for boundary layer disruption
Surface Modifications
Altering surface properties to enhance convection:
Emissivity Treatments
– Black oxide: Increases emissivity to 0.7-0.9
– Anodizing: Controlled emissivity from 0.4-0.9
– Paints and coatings: Customizable emissivity up to 0.98Wettability Control
– Hydrophilic coatings: Enhance liquid cooling
– Hydrophobic surfaces: Prevent condensation issues
– Patterned wettability: Directed condensate flow
Practical Implementation Example
For a rodless pneumatic cylinder operating in a high-temperature environment:
| Enhancement Method | Implementation | h Improvement | Temperature Reduction |
|---|---|---|---|
| Pin Fins (6mm) | Aluminum clip-on fins, 10mm spacing | 180% | 12°C |
| Directed Airflow | 80mm, 2W DC fan at 1.5 m/s | 320% | 18°C |
| Surface Treatment | Black anodizing | 40% | 3°C |
| Combined Approach | All methods integrated | 450% | 24°C |
Nusselt Number Correlation for Design Calculations
For engineering calculations, the Nusselt number4 (Nu) provides a dimensionless approach to convection:
Nu = hL/k
Where:
- L = Characteristic length
- k = Fluid thermal conductivity
For forced convection over a flat plate:
Nu = 0.664Re^(1/2)Pr^(1/3) (laminar flow)
Nu = 0.037Re^(4/5)Pr^(1/3) (turbulent flow)
Where:
- Re = Reynolds number (velocity × length × density / viscosity)
- Pr = Prandtl number (specific heat × viscosity / thermal conductivity)
These correlations allow engineers to predict convection coefficients for different configurations and optimize cooling strategies accordingly.
Radiation Efficiency Model: When Does Thermal Radiation Matter in Pneumatic Systems?
Radiation is often overlooked in pneumatic system thermal management, but it can account for 15-30% of total heat transfer in many applications. Understanding when and how to optimize radiative heat transfer is crucial for comprehensive thermal management.
Radiation heat transfer follows the Stefan-Boltzmann Law5: Q = εσA(T₁⁴-T₂⁴), where ε is surface emissivity, σ is the Stefan-Boltzmann constant, A is surface area, and T₁ and T₂ are absolute temperatures of the emitting surface and surroundings. Radiation efficiency in pneumatic systems depends primarily on surface emissivity, temperature differential, and view factors between components and their environment.
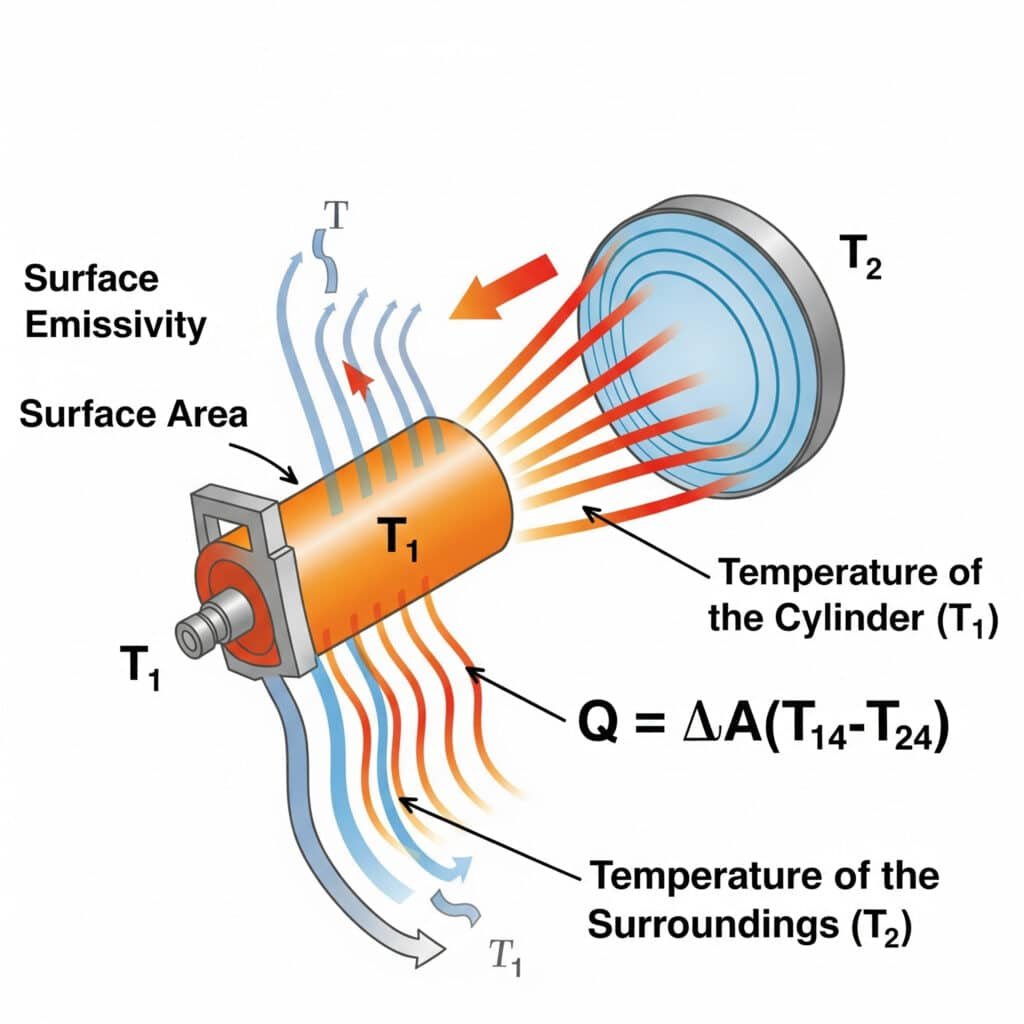
I recently helped a semiconductor equipment manufacturer in Oregon resolve overheating issues with their precision rodless cylinders. Their engineers had focused exclusively on conduction and convection but overlooked radiation. By applying a high-emissivity coating (increasing ε from 0.11 to 0.92), we enhanced radiative heat transfer by over 700%. This simple, passive solution reduced operating temperatures by 9°C without any moving parts or energy consumption—a critical requirement in their cleanroom environment.
Radiation Heat Transfer Fundamentals
The basic equation governing radiative heat transfer is:
Q = εσA(T₁⁴-T₂⁴)
Where:
- Q = Heat transfer rate (W)
- ε = Emissivity (dimensionless, 0-1)
- σ = Stefan-Boltzmann constant (5.67 × 10⁻⁸ W/m²·K⁴)
- A = Surface area (m²)
- T₁ = Surface absolute temperature (K)
- T₂ = Surroundings absolute temperature (K)
Surface Emissivity Values for Common Pneumatic Materials
| Material/Surface | Emissivity (ε) | Radiation Efficiency | Enhancement Potential |
|---|---|---|---|
| Polished Aluminum | 0.04-0.06 | Very Poor | >1500% improvement possible |
| Anodized Aluminum | 0.7-0.9 | Excellent | Already optimized |
| Stainless Steel (polished) | 0.07-0.14 | Poor | >600% improvement possible |
| Stainless Steel (oxidized) | 0.6-0.85 | Good | Moderate improvement possible |
| Steel (polished) | 0.07-0.10 | Poor | >900% improvement possible |
| Steel (oxidized) | 0.7-0.9 | Excellent | Already optimized |
| Painted Surfaces | 0.8-0.98 | Excellent | Already optimized |
| PTFE (white) | 0.8-0.9 | Excellent | Already optimized |
| Nitrile Rubber | 0.86-0.94 | Excellent | Already optimized |
View Factor Considerations
Radiation exchange depends not just on emissivity but also on geometric relationships between surfaces:
F₁₂ = Fraction of radiation leaving surface 1 that strikes surface 2
For complex geometries, view factors can be calculated using:
- Analytical solutions for simple geometries
- View factor algebra for combining known solutions
- Numerical methods for complex arrangements
- Empirical approximations for practical engineering
Temperature Dependence of Radiation
The fourth-power temperature relationship makes radiation particularly effective at higher temperatures:
| Surface Temperature | Percentage of Heat Transfer by Radiation* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Assuming natural convection conditions, ε = 0.8, 25°C ambient
Radiation Efficiency Enhancement Strategies
Based on my experience with industrial pneumatic systems, here are the most effective approaches for improving radiation heat transfer:
Surface Emissivity Modification
High-Emissivity Coatings
– Black anodizing for aluminum (ε ≈ 0.8-0.9)
– Black oxide for steel (ε ≈ 0.7-0.8)
– Specialty ceramic coatings (ε ≈ 0.9-0.98)Surface Texturing
– Micro-roughening increases effective emissivity
– Porous surfaces enhance radiative properties
– Combined emissivity/convection enhancements
Environmental Optimization
Surroundings Temperature Management
– Shielding from hot equipment/processes
– Cool walls/ceilings for better radiation exchange
– Reflective barriers to direct radiation to cooler surfacesView Factor Improvement
– Orientation to maximize exposure to cool surfaces
– Removal of blocking objects
– Reflectors to improve radiation exchange with cooler areas
Case Study: Radiation Enhancement in Precision Pneumatics
For a high-precision rodless cylinder in a cleanroom environment:
| Parameter | Original Design | Radiation-Enhanced Design | Improvement |
|---|---|---|---|
| Surface Material | Polished Aluminum (ε ≈ 0.06) | Ceramic-Coated Aluminum (ε ≈ 0.94) | 1467% increase in emissivity |
| Radiation Heat Transfer | 2.1W | 32.7W | 1457% increase in radiation |
| Operating Temperature | 68°C | 59°C | 9°C reduction |
| Component Life | 8 months | >24 months | 3× improvement |
| Implementation Cost | – | $175 per cylinder | 4.2 month payback |
Radiation vs. Other Heat Transfer Modes
Understanding when radiation dominates is crucial for efficient thermal management:
| Condition | Conduction Dominance | Convection Dominance | Radiation Dominance |
|---|---|---|---|
| Temperature Range | Low to High | Low to Medium | Medium to High |
| Material Properties | High k materials | Low k, high surface area | High ε surfaces |
| Environmental Factors | Good thermal contact | Moving air, fans | Large temperature differential |
| Space Constraints | Tight packaging | Open air flow | View to cooler surroundings |
| Best Applications | Component interfaces | General cooling | Hot surfaces, vacuum, still air |
Conclusion
Mastering heat transfer principles—conduction coefficient calculation, convection enhancement methods, and radiation efficiency modeling—provides the foundation for effective thermal management in pneumatic systems. By applying these principles, you can reduce operating temperatures, extend component life, and improve energy efficiency while ensuring reliable operation even in challenging environments.
FAQs About Heat Transfer in Pneumatic Systems
What is the typical temperature rise in pneumatic cylinders during operation?
Pneumatic cylinders typically experience temperature rises of 20-40°C above ambient during continuous operation. This rise results from friction between seals and cylinder walls, compression heating of air, and mechanical work being converted to heat. Rodless cylinders often experience higher temperature rises (30-50°C) due to their more complex sealing systems and concentrated heat generation in the bearing/seal assembly.
How does operating pressure affect heat generation in pneumatic systems?
Operating pressure has a significant impact on heat generation, with higher pressures creating more heat through several mechanisms. Each 1 bar increase in operating pressure typically increases heat generation by 8-12% due to greater friction forces between seals and surfaces, higher compression heating, and increased leakage-related losses. This relationship is approximately linear within normal operating ranges (3-10 bar).
What’s the optimal cooling approach for pneumatic components in different environments?
The optimal cooling approach varies by environment: in clean, moderate-temperature settings (15-30°C), natural convection with proper component spacing is often sufficient. In high-temperature environments (30-50°C), forced convection using fans or compressed air becomes necessary. In extremely hot conditions (>50°C) or where airflow is restricted, active cooling methods like thermoelectric coolers or liquid cooling may be required. In all cases, maximizing radiation through high-emissivity surfaces provides additional passive cooling.
How do I calculate the total heat transfer from a pneumatic component?
Calculate total heat transfer by summing the contributions from each mechanism: Qtotal = Qconduction + Qconvection + Qradiation. For conduction, use Q = kA(T₁-T₂)/L for each heat path. For convection, use Q = hA(Ts-T∞) with appropriate convection coefficients. For radiation, use Q = εσA(T₁⁴-T₂⁴). In most industrial pneumatic applications operating at 30-80°C, the approximate distribution is 20-40% conduction, 40-70% convection, and 10-30% radiation.
What’s the relationship between temperature and pneumatic component life?
Component life decreases exponentially with increasing temperature, following a modified Arrhenius relationship. As a rule of thumb, every 10°C increase in operating temperature reduces seal and component life by 40-50%. This means a component operating at 70°C might last only one-third as long as the same component at 50°C. This relationship is particularly critical for polymer components like seals, bearings, and gaskets, which often determine the maintenance interval for pneumatic systems.
-
Provides a foundational explanation of Fourier’s Law, the fundamental principle that describes how heat is conducted through solid materials based on their thermal conductivity and temperature gradient. ↩
-
Explains the function and types of Thermal Interface Materials (TIMs), which are used to fill microscopic air gaps between components to improve heat conduction and reduce thermal resistance. ↩
-
Details the principles of Newton’s Law of Cooling, which governs how objects cool by transferring heat to the surrounding fluid via convection, a key factor in system cooling design. ↩
-
Offers an in-depth look at the Nusselt number, a critical dimensionless quantity in fluid dynamics and heat transfer that represents the ratio of convective to conductive heat transfer across a boundary. ↩
-
Describes the Stefan-Boltzmann Law, the fundamental physical principle that quantifies the total energy radiated by a black body, which is essential for calculating heat loss from hot surfaces. ↩


