
¿Ha notado alguna vez vibraciones misteriosas en sus conductos neumáticos? ¿O variaciones de fuerza inexplicables en sus cilindros a pesar de una presión de suministro estable? Estos fenómenos no son aleatorios: son el resultado de ondas de presión que se propagan por su sistema, creando efectos que pueden ir desde pequeñas ineficiencias hasta fallos catastróficos.
Las fluctuaciones de presión en los sistemas neumáticos son fenómenos ondulatorios que se propagan a velocidades cercanas al velocidad del sonido1creando efectos dinámicos, incluida la resonancia, ondas estacionarias2y la amplificación de la presión. Comprender estas fluctuaciones es crucial porque pueden causar fatiga en los componentes, inestabilidad en el control y... pérdidas de energía de 10-25% en sistemas industriales típicos3.
El mes pasado, trabajé como consultor para una planta de montaje de automóviles de Tennessee en la que un sistema de sujeción neumática crítico experimentaba variaciones de fuerza intermitentes a pesar de que la presión de suministro era estable. Su equipo de mantenimiento había sustituido válvulas, reguladores e incluso todo el unidad de preparación de aire4 sin éxito. Analizando la dinámica de las ondas de presión, en particular los patrones de ondas estacionarias en sus conductos de suministro, descubrimos que funcionaban a una frecuencia que creaba interferencias destructivas en el cilindro. Un simple ajuste de la longitud de la línea eliminó el problema y les ahorró semanas de retrasos en la producción. Permítame mostrarle cómo la comprensión de la teoría de las fluctuaciones de presión puede transformar la fiabilidad de su sistema neumático.
Índice
- Velocidad de propagación de ondas: ¿A qué velocidad viajan las perturbaciones de presión en su sistema?
- Verificación de ondas estacionarias: ¿Cómo crean problemas de rendimiento las frecuencias resonantes?
- Métodos de atenuación de impulsos: ¿Qué técnicas amortiguan eficazmente las oscilaciones de presión destructivas?
- Conclusión
- Preguntas frecuentes sobre las fluctuaciones de presión en sistemas neumáticos
Velocidad de propagación de ondas: ¿A qué velocidad viajan las perturbaciones de presión en su sistema?
Comprender la rapidez con que se propagan las perturbaciones de presión a través de los sistemas neumáticos es fundamental para predecir y controlar sus efectos. La velocidad de propagación determina el tiempo de respuesta del sistema, las frecuencias de resonancia y el potencial de interferencia destructiva.
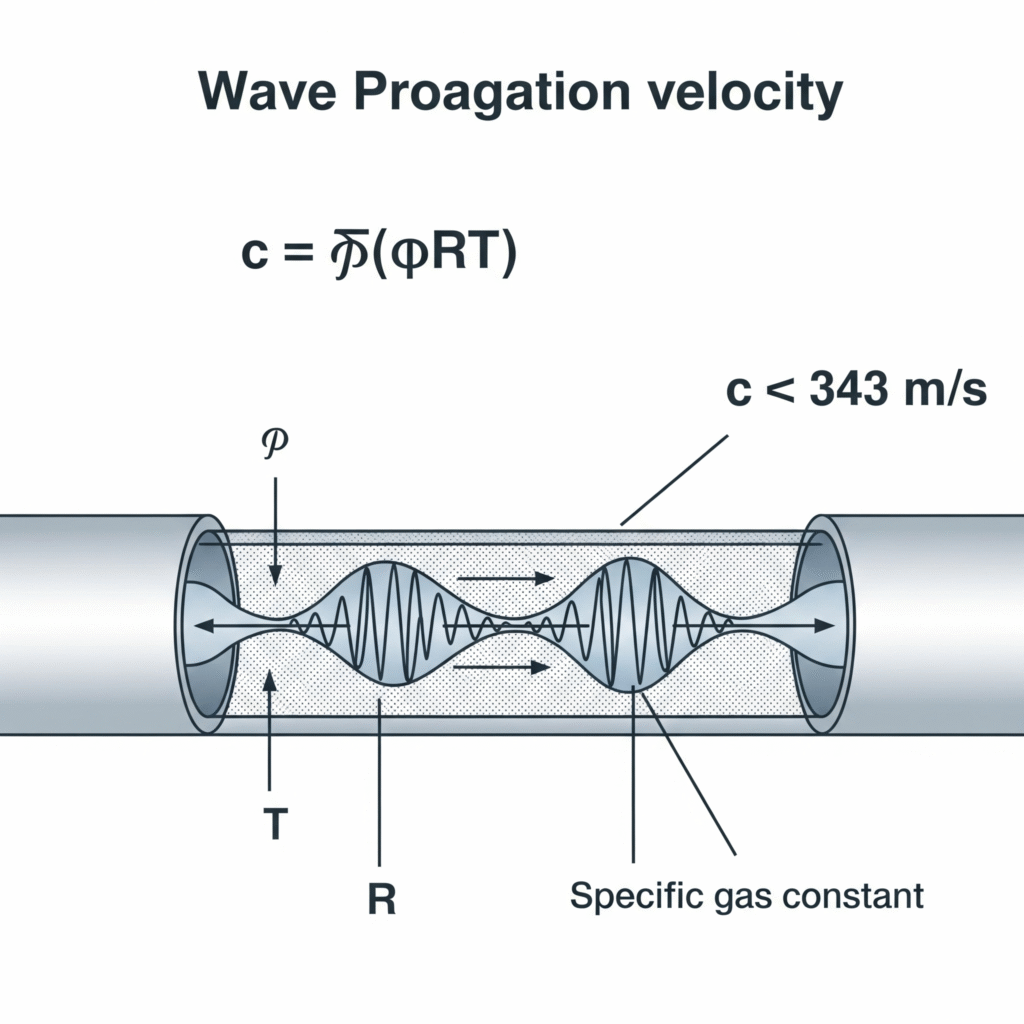
Las ondas de presión en los sistemas neumáticos viajan a la velocidad del sonido en el medio gaseoso, que puede calcularse mediante la fórmula c = √(γRT), donde γ es el coeficiente de calor específico, R es la constante específica del gas y T es la temperatura absoluta. Para el aire a 20 °C, esto equivale aproximadamente a 343 m/s, aunque esta velocidad se ve modificada por factores como la elasticidad de la tubería, la compresibilidad del gas y las condiciones del flujo.
Hace poco ayudé a solucionar un problema en una máquina de montaje de precisión en Suiza, donde las pinzas neumáticas experimentaban un retraso de 12 ms entre la activación y la aplicación de la fuerza, una eternidad en un entorno de producción de alta velocidad. Sus ingenieros habían supuesto una transmisión instantánea de la presión. Midiendo la velocidad real de propagación de la onda en su sistema (328 m/s) y teniendo en cuenta la longitud de la línea de 4 metros, calculamos un tiempo de transmisión teórico de 12,2 ms, que coincidía casi exactamente con el retardo observado. La reubicación de las válvulas más cerca de los actuadores redujo este retardo a 3 ms y aumentó la tasa de producción en 14%.
Ecuaciones fundamentales de velocidad de onda
La ecuación básica de la velocidad de propagación de las ondas de presión en un gas es:
c = √(γRT)
Dónde:
- c = Velocidad de propagación de las ondas (m/s)
- γ = Relación de calor específico (1,4 para el aire)
- R = Constante específica de los gases (287 J/kg-K para el aire)
- T = Temperatura absoluta (K)
Para el aire a 20°C (293K), esto da:
c = √(1,4 × 287 × 293) = 343 m/s
Velocidad de onda modificada en líneas neumáticas
En los sistemas neumáticos reales, la velocidad de onda efectiva se ve modificada por la elasticidad de la tubería y otros factores según la fórmula:
c_eff = c / √(1 + (Dψ/Eh))
Dónde:
- c_eff = Velocidad de onda efectiva (m/s)
- D = Diámetro del tubo (m)
- ψ = Factor de compresibilidad del gas
- E = Módulo elástico del material de la tubería (Pa)
- h = Espesor de la pared del tubo (m)
Efectos de la temperatura y la presión en la velocidad de las ondas
La velocidad de las ondas varía en función de las condiciones de funcionamiento:
| Temperatura | Presión | Velocidad de las ondas en el aire | Implicaciones prácticas |
|---|---|---|---|
| 0°C (273K) | 1 bar | 331 m/s | Respuesta más lenta en ambientes fríos |
| 20°C (293K) | 1 bar | 343 m/s | Condición de referencia estándar |
| 40°C (313K) | 1 bar | 355 m/s | Respuesta más rápida en entornos cálidos |
| 20°C (293K) | 6 bar | 343 m/s* | La presión tiene un efecto directo mínimo sobre la velocidad |
*Nota: Mientras que la velocidad de onda básica es independiente de la presión, la velocidad efectiva en sistemas reales puede verse afectada por cambios inducidos por la presión en la elasticidad de la tubería y el comportamiento del gas.
Cálculo práctico del tiempo de propagación de las ondas
Para un sistema neumático con:
- Longitud de la línea (L): 5 metros
- Temperatura de funcionamiento: 20°C (c = 343 m/s)
- Material de la tubería: Tubo de poliuretano (modifica la velocidad en aproximadamente 5%)
La velocidad de onda efectiva sería:
c_eff = 343 × 0,95 = 326 m/s
Y el tiempo de propagación de la onda sería:
t = L/c_eff = 5/326 = 0,0153 segundos (15,3 milisegundos)
Esto representa el tiempo mínimo necesario para que un cambio de presión se desplace de un extremo a otro de la línea, un factor crítico en aplicaciones de alta velocidad.
Técnicas de medición de la velocidad de las ondas
Se pueden utilizar varios métodos para medir la velocidad real de las ondas en los sistemas neumáticos:
Método de doble sensor de presión
- Instale los sensores de presión a distancias conocidas
- Crear un impulso de presión (apertura rápida de la válvula)
- Medir el tiempo de retardo entre el aumento de presión en cada sensor
- Calcular la velocidad como la distancia dividida por el tiempo de retardo
Método de la frecuencia resonante
- Crear oscilaciones de presión en un tubo cerrado
- Medir la frecuencia de resonancia fundamental (f)
- Calcular la velocidad utilizando c = 2Lf para un tubo de extremo cerrado
- Verificar con armónicos (múltiplos impares de la fundamental)
Método de tiempo de reflexión
- Instalar un sensor de presión cerca de una válvula
- Crear un impulso de presión abriendo rápidamente la válvula
- Medir el tiempo entre el pulso inicial y el pulso reflejado
- Calcular la velocidad como 2L dividido por el tiempo de reflexión
Estudio de caso: Impacto de la velocidad de las olas en la respuesta del sistema
Para un efector final robótico con pinzas neumáticas:
| Parámetro | Diseño original (5m líneas) | Diseño optimizado (líneas de 1 m) | Mejora |
|---|---|---|---|
| Longitud de línea | 5 metros | 1 metro | Reducción 80% |
| Tiempo de propagación de la onda | 15,3 ms | 3,1 ms | 12,2 ms más rápido |
| Tiempo de acumulación de presión | 28 ms | 9 ms | 19 ms más rápido |
| Estabilidad de la fuerza de agarre | Variación ±12% | Variación ±3% | 75% mejora |
| Duración del ciclo | 1,2 segundos | 0,95 segundos | 21% más rápido |
| Tasa de producción | 3000 piezas/hora | 3780 piezas/hora | Aumento 26% |
Este caso práctico demuestra cómo comprender y optimizar la propagación de las ondas puede repercutir significativamente en el rendimiento del sistema.
Verificación de ondas estacionarias: ¿Cómo crean problemas de rendimiento las frecuencias resonantes?
Las ondas estacionarias se producen cuando las ondas de presión se reflejan e interfieren entre sí, creando patrones fijos de nodos y antinodos de presión. Estos fenómenos resonantes pueden causar graves problemas de rendimiento en los sistemas neumáticos si no se comprenden y gestionan adecuadamente.
Las ondas estacionarias en los sistemas neumáticos se producen cuando las ondas de presión se reflejan en los límites e interfieren constructivamente, creando frecuencias resonantes en las que se amplifican las fluctuaciones de presión. Estas resonancias siguen la fórmula f = nc/2L para tubos cerrados, donde n es el número armónico, c es la velocidad de la onda y L es la longitud del tubo. La verificación experimental mediante sensores de presión, acelerómetros y mediciones acústicas confirma estas predicciones teóricas y orienta estrategias de mitigación eficaces.
Durante un proyecto reciente con un fabricante de dispositivos médicos de Massachusetts, su sistema de posicionamiento neumático de precisión mostraba misteriosas fluctuaciones de fuerza a determinadas frecuencias de funcionamiento. Al realizar pruebas de verificación de ondas estacionarias, identificamos que su línea de suministro de 2,1 metros tenía una resonancia fundamental a 81 Hz, que coincidía exactamente con la frecuencia de ciclo de su actuador. Esta resonancia amplificaba las fluctuaciones de presión en 320%. Al ajustar la longitud de la línea a 1,8 metros, desplazamos la frecuencia resonante fuera de su rango operativo y eliminamos por completo el problema, mejorando la precisión de posicionamiento de ±0,8 mm a ±0,15 mm.
Fundamentos de las ondas estacionarias
Las ondas estacionarias se forman cuando las ondas incidentes y reflejadas interfieren, creando patrones fijos de nodos de presión (fluctuación mínima) y antinodos (fluctuación máxima).
Las frecuencias de resonancia de una línea neumática dependen de las condiciones de contorno:
Para un conducto con extremos cerrados (lo más habitual en sistemas neumáticos):
f = nc/2L
Dónde:
- f = Frecuencia de resonancia (Hz)
- n = Número armónico (1, 2, 3, etc.)
- c = Velocidad de las ondas (m/s)
- L = Longitud de la línea (m)
Para una línea con un extremo abierto:
f = (2n-1)c/4L
Para una línea con los dos extremos abiertos (poco frecuente en neumática):
f = nc/2L
Métodos de verificación experimental
Varias técnicas pueden verificar los patrones de ondas estacionarias en sistemas neumáticos:
Conjunto de varios sensores de presión
- Instale transductores de presión a intervalos regulares a lo largo de la línea neumática
- Excitar el sistema con un barrido de frecuencias o un impulso.
- Registrar las fluctuaciones de presión en cada lugar
- Mapear la amplitud de presión frente a la posición para identificar nodos y antinodos.
- Comparar las frecuencias medidas con las predicciones teóricas
Correlación acústica
- Utilizar sensores acústicos (micrófonos) para detectar el sonido a partir de las fluctuaciones de presión.
- Correlacionar la intensidad sonora con la frecuencia de funcionamiento
- Identificar los picos de intensidad sonora correspondientes a las frecuencias resonantes.
- Comprobar que los picos se producen en las frecuencias previstas
Mediciones del acelerómetro
- Montar acelerómetros en líneas y componentes neumáticos
- Medición de la amplitud de las vibraciones en toda la gama de frecuencias
- Identificar picos resonantes en el espectro de vibraciones
- Correlación con las frecuencias de ondas estacionarias previstas
Cálculo práctico de la frecuencia de las ondas estacionarias
Para un sistema neumático típico con:
- Longitud de la línea (L): 3 metros
- Velocidad de las ondas (c): 343 m/s
- Configuración de extremos cerrados
La frecuencia de resonancia fundamental sería:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
Y los armónicos serían:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Estas frecuencias representan posibles puntos problemáticos en los que las fluctuaciones de presión pueden amplificarse.
Patrones de ondas estacionarias y sus efectos
| Armónico | Patrón nodo/antinodo | Efectos del sistema | Componentes críticos afectados |
|---|---|---|---|
| Fundamental (n=1) | Un antinudo de presión en el centro | Grandes variaciones de presión en la línea media | Componentes en línea, racores |
| Segundo (n=2) | Dos antinodos, nodo en el centro | Variaciones de presión cerca de los extremos | Válvulas, actuadores, reguladores |
| Tercero (n=3) | Tres antinodos, dos nodos | Patrón de presión complejo | Múltiples componentes del sistema |
| Cuarto (n=4) | Cuatro antinodos, tres nodos | Oscilaciones de alta frecuencia | Juntas, componentes pequeños |
Caso práctico de verificación experimental
Para un sistema de posicionamiento neumático de precisión que experimenta un rendimiento incoherente:
| Parámetro | Predicción teórica | Medición experimental | Correlación |
|---|---|---|---|
| Frecuencia fundamental | 81,2 Hz | 79,8 Hz | 98.3% |
| Segundo armónico | 162,4 Hz | 160,5 Hz | 98.8% |
| Tercer armónico | 243,6 Hz | 240,1 Hz | 98.6% |
| Amplificación de la presión | 3:1 en resonancia (estimado) | 3,2:1 en resonancia (medido) | 93.8% |
| Ubicación de los nodos | 0, 1,05, 2,1 metros | 0, 1,08, 2,1 metros | 97.2% |
Este estudio de caso demuestra la excelente concordancia entre las predicciones teóricas y las mediciones experimentales de los fenómenos de ondas estacionarias.
Implicaciones prácticas de las ondas estacionarias
Las ondas estacionarias plantean varios problemas importantes en los sistemas neumáticos:
Amplificación de la presión
- Las fluctuaciones pueden amplificarse 3-5× en resonancia
- Puede superar la presión nominal de los componentes
- Crea variaciones de fuerza en los actuadoresFatiga de los componentes
- Los ciclos de presión de alta frecuencia aceleran el desgaste de las juntas
- Las vibraciones provocan el aflojamiento de los racores y fugas
- Reduce la vida útil del sistema en 30-70% en casos graves.Control de la inestabilidad
- Los sistemas de retroalimentación pueden oscilar a frecuencias resonantes
- El control de la posición y la fuerza se vuelve impredecible
- Puede crear oscilaciones autorreforzadasPérdidas de energía
- Las ondas estacionarias representan energía atrapada
- Puede aumentar el consumo de energía en 10-30%
- Reduce la eficiencia global del sistema
Métodos de atenuación de impulsos: ¿Qué técnicas amortiguan eficazmente las oscilaciones de presión destructivas?
El control de las oscilaciones de presión es esencial para un funcionamiento fiable de los sistemas neumáticos. Se pueden emplear varios métodos de atenuación para reducir o eliminar las problemáticas oscilaciones de presión.
La atenuación de los impulsos de presión en los sistemas neumáticos puede conseguirse mediante varios métodos: cámaras de volumen que absorben la energía mediante la compresión del gas, elementos restrictivos que crean amortiguación mediante efectos viscosos, resonadores sintonizados que cancelan frecuencias específicas y sistemas de cancelación activos que generan contraimpulsos. Una atenuación eficaz requiere adaptar el método al contenido de frecuencia específico y a la amplitud de las fluctuaciones de presión.
Hace poco trabajé con un fabricante de equipos de envasado de Illinois cuyo sistema neumático de alta velocidad experimentaba graves fluctuaciones de presión que provocaban fuerzas de sellado incoherentes. Sus ingenieros habían probado tanques receptores básicos sin éxito. Mediante un análisis detallado de los impulsos de presión, descubrimos que su sistema tenía múltiples componentes de frecuencia que requerían distintos enfoques de atenuación. Mediante la aplicación de una solución híbrida que combinaba un Resonador Helmholtz5 sintonizados con su oscilación dominante de 112 Hz y una serie de orificios de restricción, redujimos las fluctuaciones de presión en 94% y eliminamos por completo las inconsistencias de sellado.
Mecanismos fundamentales de atenuación
Se pueden utilizar varios mecanismos físicos para atenuar los impulsos de presión:
Atenuación basada en el volumen
Funciona a través de la compresibilidad del gas:
- Proporciona un elemento de conformidad que absorbe la energía de la presión
- Más eficaz para las fluctuaciones de baja frecuencia
- Aplicación sencilla con una caída de presión mínima
Atenuación basada en restricciones
Funciona por disipación viscosa:
- Convierte la energía de presión en calor a través de la fricción
- Eficaz en una amplia gama de frecuencias
- Crea una caída de presión permanente
Atenuación basada en resonadores
Funciona mediante interferencia destructiva sintonizada:
- Cancela componentes de frecuencia específicos
- Gran eficacia para frecuencias específicas
- Impacto mínimo en el flujo en estado estacionario
Atenuación basada en el material
Funciona gracias a la flexibilidad y amortiguación de las paredes:
- Absorbe energía mediante la deformación de la pared
- Proporciona atenuación de banda ancha
- Puede integrarse en componentes existentes
Principios de diseño de la cámara de volumen
Las cámaras de volumen (tanques receptores) son los dispositivos de atenuación más comunes:
La eficacia de una cámara de volumen depende de la relación entre el volumen de la cámara y el volumen de la línea:
Relación de atenuación = 1 + (Vc/Vl)
Dónde:
- Vc = Volumen de la cámara
- Vl = Volumen de la línea
Para el análisis en función de la frecuencia, la relación de transmisión es:
TR = 1/√(1 + (ωVc/Zc)²)
Dónde:
- ω = Frecuencia angular (2πf)
- Zc = Impedancia característica de la línea
Atenuación de elementos restrictivos
Los orificios, los materiales porosos y los pasos largos y estrechos crean atenuación por efectos viscosos:
La caída de presión a través de una restricción es la siguiente
ΔP = k(ρv²/2)
Dónde:
- k = Coeficiente de pérdidas
- ρ = Densidad del gas
- v = Velocidad
La atenuación proporcionada aumenta con:
- Mayor velocidad de flujo
- Mayor longitud de restricción
- Menor diámetro de paso
- Flujo más tortuoso
Sistemas de atenuación por resonador
Los resonadores sintonizados proporcionan una atenuación de frecuencia específica:
Resonador Helmholtz
Una cámara de volumen con un cuello estrecho, sintonizada a una frecuencia específica:
f = (c/2π)√(A/VL)
Dónde:
- f = Frecuencia de resonancia
- c = Velocidad del sonido
- A = área de la sección transversal del cuello
- V = Volumen de la cámara
- L = Longitud efectiva del cuello
Resonador de cuarto de onda
Tubo de longitud determinada abierto por un extremo:
f = c/4L
Dónde:
- L = Longitud del tubo
Resonadores de ranura lateral
Múltiples ramas sintonizadas para contenidos de frecuencias complejas:
- Cada rama se dirige a una frecuencia específica
- Puede tratar varios armónicos simultáneamente
- Impacto mínimo en el flujo principal
Sistemas de cancelación activa
Sistemas avanzados que generan contraimpulsos:
Etapa de detección
- Detectar las ondas de presión entrantes
- Analizar el contenido frecuencial y la amplitudFase de procesamiento
- Calcular la señal de cancelación necesaria
- Tener en cuenta la dinámica y los retrasos del sistemaEtapa de actuación
- Generar ondas de contrapresión
- Tiempo preciso para la interferencia destructiva
Comparación de la atenuación
| Método | Baja frecuencia (<50 Hz) | Frecuencia media (50-200 Hz) | Alta frecuencia (>200 Hz) | Caída de presión | Complejidad |
|---|---|---|---|---|---|
| Cámara de volumen | Excelente (>90%) | Moderado (40-70%) | Pobre (<30%) | Muy bajo | Bajo |
| Orificio restrictivo | Pobre (<30%) | Bueno (60-80%) | Excelente (>80%) | Alta | Bajo |
| Resonador Helmholtz | Poca resonancia exterior | Excelente en resonancia | Poca resonancia exterior | Bajo | Medio |
| Tubo de cuarto de onda | Poca resonancia exterior | Excelente en resonancia | Poca resonancia exterior | Bajo | Medio |
| Resonadores múltiples | Moderado (40-60%) | Excelente (>80%) | Bueno (60-80%) | Bajo | Alta |
| Cancelación activa | Excelente (>90%) | Excelente (>90%) | Bien (70-85%) | Ninguno | Muy alta |
| Sistemas híbridos | Excelente (>90%) | Excelente (>90%) | Excelente (>90%) | Moderado | Alta |
Aplicación práctica de la atenuación
Para una atenuación eficaz de los impulsos de presión:
Caracterizar las fluctuaciones
- Medir el contenido de amplitud y frecuencia
- Identificar las frecuencias dominantes
- Determinar si es necesario atenuar la banda ancha o frecuencias específicasSeleccionar los métodos adecuados
- Para frecuencias bajas: Cámaras de volumen
- Para frecuencias específicas: Resonadores sintonizados
- Para la atenuación de banda ancha: Restricciones o enfoques híbridos
- Para aplicaciones críticas: Cancelación activaOptimizar la colocación
- Cerca de las fuentes para evitar la propagación
- Cerca de componentes sensibles para protegerlos
- En lugares estratégicos para romper los patrones de ondas estacionariasVerificar el rendimiento
- Medición antes/después de la atenuación
- Confirmar todas las condiciones de funcionamiento
- Garantizar que no haya consecuencias imprevistas
Caso práctico: Atenuación multimétodo en envases de alta velocidad
Para un sistema de estanquidad neumático de alta velocidad que experimenta fluctuaciones de presión:
| Parámetro | Antes de la atenuación | Después de la cámara de volumen | Después de la solución híbrida | Mejora |
|---|---|---|---|---|
| Baja frecuencia (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | Reducción 94% |
| Frecuencia media (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | Reducción 94% |
| Alta frecuencia (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | Reducción 90% |
| Variación de la fuerza de sellado | ±28% | ±22% | ±2,5% | 91% mejora |
| Tasa de rechazo de productos | 4.2% | 3.1% | 0.3% | Reducción 93% |
| Eficiencia del sistema | Línea de base | +4% | +12% | 12% mejora |
Este estudio de caso demuestra cómo un enfoque específico y multimétodo de la atenuación puede mejorar drásticamente el rendimiento del sistema.
Técnicas avanzadas de atenuación
Para aplicaciones especialmente exigentes:
Atenuación distribuida
Utilizar varios dispositivos pequeños en lugar de uno grande:
- Sitúa la atenuación más cerca tanto de las fuentes como de los componentes sensibles
- Rompe más eficazmente los patrones de ondas estacionarias
- Proporciona redundancia y un rendimiento más uniforme
Amortiguación selectiva en frecuencia
Centrarse en frecuencias problemáticas específicas:
- Utiliza múltiples resonadores sintonizados a distintas frecuencias
- Preserva la respuesta deseada del sistema al tiempo que elimina los problemas
- Minimiza el impacto en el rendimiento general del sistema
Sistemas adaptativos
Ajuste de la atenuación en función de las condiciones de funcionamiento:
- Utiliza sensores para controlar las fluctuaciones de presión
- Ajusta automáticamente los parámetros de atenuación
- Optimiza el rendimiento en condiciones variables
Conclusión
La comprensión de la teoría de la fluctuación de la presión -velocidad de propagación de la onda, verificación de la onda estacionaria y métodos de atenuación de impulsos- sienta las bases para un diseño fiable y eficiente de los sistemas neumáticos. La aplicación de estos principios permite eliminar misteriosos problemas de rendimiento, prolongar la vida útil de los componentes y mejorar la eficiencia del sistema, al tiempo que se garantiza un funcionamiento uniforme en todas las condiciones de funcionamiento.
Preguntas frecuentes sobre las fluctuaciones de presión en sistemas neumáticos
¿Cómo afectan las fluctuaciones de presión a la vida útil de los componentes neumáticos?
Las fluctuaciones de presión reducen significativamente la vida útil de los componentes a través de varios mecanismos: provocan un desgaste acelerado de las juntas al crear micromovimientos en las superficies de sellado; inducen la fatiga de los materiales en los diafragmas y elementos flexibles a través de ciclos de tensión repetidos; favorecen el aflojamiento de las conexiones roscadas a través de la vibración; y crean concentraciones de tensión localizadas en las transiciones geométricas. Los sistemas con fuertes fluctuaciones incontroladas de presión suelen experimentar 40-70% una menor vida útil de los componentes en comparación con los sistemas correctamente amortiguados, siendo las juntas y los diafragmas especialmente vulnerables.
¿Cuál es la relación entre la longitud de la línea y el tiempo de respuesta de la presión en los sistemas neumáticos?
La longitud de la línea afecta directamente al tiempo de respuesta de la presión siguiendo una relación sencilla: el tiempo de respuesta aumenta linealmente con la longitud de la línea a un ritmo determinado por la velocidad de propagación de la onda. Para el aire en condiciones estándar (velocidad de onda ≈ 343 m/s), cada metro de línea añade aproximadamente 2,9 milisegundos de retardo de transmisión. Sin embargo, el tiempo real de aumento de la presión suele ser de 2 a 5 veces mayor que el tiempo inicial de transmisión de la onda debido a la necesidad de múltiples reflexiones para igualar la presión. Esto significa que una línea de 5 metros puede tener un tiempo de transmisión de onda de 14,5 ms, pero un tiempo de aumento de presión de 30-70 ms.
¿Cómo puedo identificar si mi sistema neumático experimenta fluctuaciones de presión resonantes?
Las fluctuaciones de presión resonantes se manifiestan normalmente a través de varios síntomas observables: los componentes vibran a frecuencias de funcionamiento específicas pero no a otras; el rendimiento del sistema varía de forma incoherente con pequeños cambios en las condiciones de funcionamiento; hay "cantos" o "silbidos" audibles en las líneas neumáticas; los manómetros muestran lecturas oscilantes; y el rendimiento del actuador (velocidad, fuerza) varía cíclicamente. Para confirmar la resonancia, mida la presión en diferentes puntos del sistema utilizando transductores de respuesta rápida (tiempo de respuesta <1 ms) y busque patrones de ondas estacionarias en los que la amplitud de la presión varíe con la posición a lo largo de la línea.
¿Afectan las fluctuaciones de presión a la eficiencia energética de los sistemas neumáticos?
Las fluctuaciones de presión afectan significativamente a la eficiencia energética, reduciéndola normalmente en 10-25% a través de varios mecanismos: aumentan los índices de fuga al crear presiones pico más altas; desperdician energía en la compresión y expansión cíclicas; provocan un aumento de la fricción en los componentes debido a la vibración; y a menudo llevan a los operadores a aumentar la presión de suministro para compensar los problemas de rendimiento. Además, las turbulencias y la separación de flujos creadas por las fluctuaciones de presión convierten la energía útil de la presión en calor residual. Atenuar adecuadamente las fluctuaciones de presión puede mejorar el rendimiento del sistema en 5-15% sin ningún otro cambio.
¿Cómo afectan los cambios de temperatura al comportamiento de las ondas de presión en los sistemas neumáticos?
La temperatura influye significativamente en el comportamiento de las ondas de presión a través de varios mecanismos: afecta directamente a la velocidad de propagación de las ondas (aproximadamente +0,6 m/s por °C de aumento); modifica la densidad y viscosidad del gas, alterando las características de amortiguación; modifica las propiedades elásticas de las líneas neumáticas, afectando a la reflexión y transmisión de las ondas; y desplaza las frecuencias de resonancia (aproximadamente +0,17% por °C). Esta sensibilidad a la temperatura significa que un sistema que funciona perfectamente a 20 °C puede experimentar resonancias problemáticas cuando funciona a 40 °C, o que los dispositivos de atenuación ajustados para condiciones invernales pueden resultar ineficaces durante el verano.
-
Ofrece una explicación detallada de la física que subyace a la velocidad del sonido, cómo se calcula y los factores que influyen en ella. ↩
-
Ofrece una comprensión básica de los fenómenos de ondas estacionarias, incluyendo cómo se forman a partir de la interferencia y sus características clave como nodos y antinodos. ↩
-
Proporciona pruebas y estudios industriales que verifican el rango típico de pérdidas de energía causadas por ineficiencias como las fluctuaciones de presión en los sistemas neumáticos. ↩
-
Explica los componentes y el funcionamiento de una unidad de preparación de aire (FRL), esencial para mantener la calidad del aire en los sistemas neumáticos. ↩
-
Ofrece una explicación en profundidad de los principios en los que se basa un resonador de Helmholtz, un dispositivo fundamental para la atenuación de frecuencias específicas en sistemas acústicos y de fluidos. ↩


