Ingenieure stoßen bei der Volumenberechnung für abgeflachte kugelförmige Komponenten in kolbenstangenlosen Pneumatikzylindersystemen auf Verwirrung. Falsche Volumenberechnungen führen zu Druckfehlberechnungen und Systemausfällen.
Eine flache Kugel (abgeplattetes Sphäroid) hat das Volumen V = (4/3)πa²b, wobei "a" der äquatoriale Radius und "b" der polare Radius ist, wie er üblicherweise in Pneumatikspeicher1 und Dämpfungsanwendungen.
Letzten Monat habe ich Andreas, einem Konstrukteur aus Deutschland, geholfen, dessen pneumatisches Dämpfungssystem versagte, weil er für seine abgeflachten Akkumulatorkammern das Volumen einer Standardkugel anstelle eines abgeflachten Sphäroids berechnet hatte.
Inhaltsübersicht
- Was ist eine Flachkugel in pneumatischen Anwendungen?
- Wie berechnet man das Volumen einer flachen Kugel?
- Wo werden Flachkugeln in stangenlosen Zylindern verwendet?
- Wie wirkt sich die Abflachung auf Volumen und Leistung aus?
Was ist eine Flachkugel in pneumatischen Anwendungen?
Eine flache Kugel, technisch als abgeplattetes Sphäroid2ist eine dreidimensionale Form, die entsteht, wenn eine Kugel entlang einer Achse zusammengedrückt wird, und die häufig in pneumatischen Akkumulatoren und Dämpfern verwendet wird.
Eine flache Kugel entsteht durch Abflachung einer perfekten Kugel entlang ihrer vertikalen Achse, wodurch ein elliptischer Querschnitt mit unterschiedlichen horizontalen und vertikalen Radien entsteht.
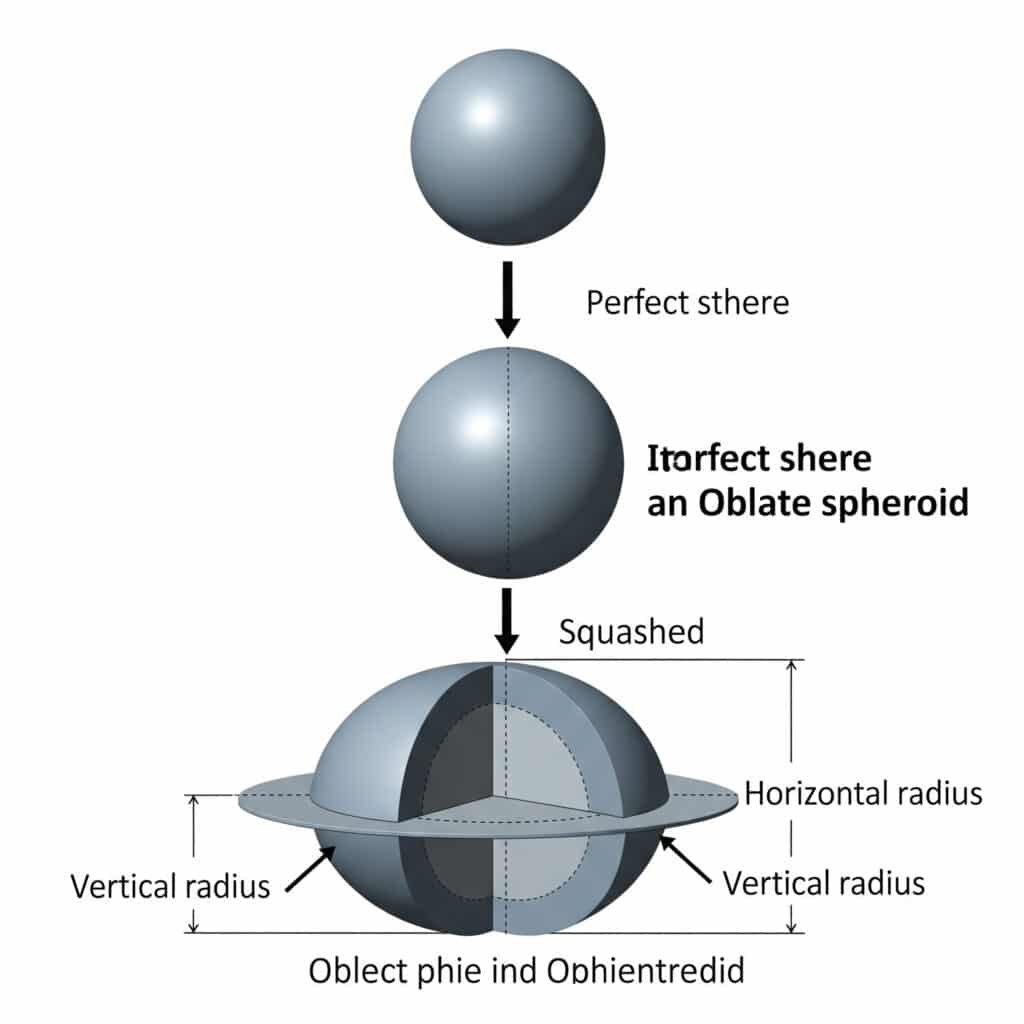
Geometrische Definition
Merkmale der Form
- Oblate Sphäroide: Geometrischer Fachbegriff
- Abgeflachte Kugel: Allgemeine industrielle Beschreibung
- Elliptisches Profil: Querschnittsansicht
- Rotationssymmetrie: Um die vertikale Achse
Schlüssel Abmessungen
- Äquatorialer Radius (a): Horizontaler Radius (größer)
- Polarradius (b): Vertikaler Radius (kleiner)
- Abflachungsgrad: b/a < 1,0
- Seitenverhältnis: Verhältnis Höhe zu Breite
Flache Sphäre vs. Perfekte Sphäre
| Charakteristisch | Perfekte Sphäre | Flache Kugel |
|---|---|---|
| Form | Einheitlicher Radius | Vertikal komprimiert |
| Volumen-Formel | (4/3)πr³ | (4/3)πa²b |
| Querschnitt | Kreis | Ellipse |
| Symmetrie | Alle Richtungen | Nur waagerecht |
Gemeinsame Abflachungsquoten
Lichtabflachung
- Ratiob/a = 0,8-0,9
- Anwendungen: Geringfügige Platzbeschränkungen
- Auswirkungen auf das Volumen: 10-20% Ermäßigung
- Leistung: Minimale Wirkung
Mäßige Abflachung
- Ratiob/a = 0,6-0,8
- Anwendungen: Standard-Akkuausführungen
- Auswirkungen auf das Volumen: 20-40% Ermäßigung
- Leistung: Spürbare Druckänderungen
Starke Abflachung
- Ratiob/a = 0,3-0,6
- Anwendungen: Starke Platzprobleme
- Auswirkungen auf das Volumen: 40-70% Ermäßigung
- Leistung: Wichtige Designüberlegungen
Pneumatische Anwendungen
Akkumulatorkammern
Ich treffe auf flache Kugeln:
- Platzbeschränkte Installationen: Höhenbegrenzungen
- Integrierte Entwürfe: Eingebaut in Maschinengestelle
- Kundenspezifische Anwendungen: Spezifische Volumenanforderungen
- Nachrüstungsprojekte: Anpassung an bestehende Räume
Dämpfungssysteme
- Dämpfung am Ende des Hubs: Anwendungen für kolbenstangenlose Zylinder
- Stoßdämpfung: Management der Stoßbelastung
- Druckregelung: Reibungslose Steuerung des Betriebs
- Rauschunterdrückung: Leiserer Systembetrieb
Überlegungen zur Herstellung
Produktionsmethoden
- Tiefziehen: Blechbearbeitung
- Hydroforming: Präzises Formgebungsverfahren
- Bearbeitung: Maßgeschneiderte Einzelanfertigungen
- Gießen: Großserienproduktion
Auswahl des Materials
- Stahl: Hochdruckanwendungen
- Aluminium: Gewichtsempfindliche Designs
- Rostfreier Stahl: Korrosive Umgebungen
- Zusammengesetzte Materialien: Spezialisierte Anforderungen
Wie berechnet man das Volumen einer flachen Kugel?
Für die Berechnung des Volumens einer flachen Kugel ist die Formel für abgeplattete Sphäroide erforderlich, bei der sowohl die äquatorialen als auch die polaren Radien gemessen werden, um ein genaues pneumatisches System auszulegen.
Verwenden Sie die Formel V = (4/3)πa²b, wobei "a" der äquatoriale Radius (horizontal) und "b" der polare Radius (vertikal) ist, um das Volumen einer flachen Kugel genau zu berechnen.
Aufschlüsselung der Volumenformel
Standard-Formel
V = (4/3)πa²b
- V: Volumen in Kubikeinheiten
- π: 3,14159 (mathematische Konstante)
- a: Äquatorialradius (horizontal)
- b: Polarradius (vertikal)
- 4/3: Volumenkoeffizient des Sphäroids
Komponenten der Formel
- Äquatoriale Zoneπa² (horizontaler Querschnitt)
- Polare Skalierungb-Faktor (vertikale Kompression)
- Volumen-Koeffizient: 4/3 (geometrische Konstante)
- Ergebnis Einheiten: Anpassung des Eingaberadius in kubischen Einheiten
Schritt-für-Schritt-Berechnung
Messverfahren
- Messung des äquatorialen Durchmessers: Breiteste horizontale Abmessung
- Berechnen des Äquatorialradiusa = Durchmesser ÷ 2
- Messung des Poldurchmessers: Vertikales Höhenmaß
- Berechnen des Polarradiusb = Höhe ÷ 2
- Formel anwenden: V = (4/3)πa²b
Berechnungsbeispiel
Für einen Pneumatikspeicher:
- Äquatorialer Durchmesser: 100mm → a = 50mm
- Polarer Durchmesser: 60mm → b = 30mm
- Band: V = (4/3)π(50)²(30)
- Ergebnis: V = (4/3)π(2500)(30) = 314,159 mm³
Beispiele für Volumenberechnungen
| Äquatorialer Radius | Polarer Radius | Abflachungsverhältnis | Band | Vergleich mit Sphere |
|---|---|---|---|---|
| 50mm | 50mm | 1.0 | 523.599 mm³ | 100% (perfekte Kugel) |
| 50mm | 40mm | 0.8 | 418.879 mm³ | 80% |
| 50mm | 30mm | 0.6 | 314,159 mm³ | 60% |
| 50mm | 20mm | 0.4 | 209.440 mm³ | 40% |
Berechnungs-Tools
Manuelle Berechnung
- Wissenschaftlicher Taschenrechner: Mit π-Funktion
- Überprüfung der Formel: Eingaben doppelt prüfen
- Konsistenz der Einheit: Gleiche Einheiten durchgehend beibehalten
- Präzision: Berechnen Sie auf die entsprechenden Dezimalstellen
Digitale Werkzeuge
- Technische Software: CAD-Volumenberechnungen
- Online-Rechner: Oblate Sphäroide Werkzeuge
- Formeln für die Tabellenkalkulation: Automatisierte Berechnungen
- Mobile Anwendungen: Feldberechnungstools
Häufige Berechnungsfehler
Fehler bei der Messung
- Radius vs. Durchmesser: Verwendung der falschen Dimension
- Achsenverwirrung: Vermischung von horizontalen/vertikalen Messungen
- Inkonsistenz der Einheiten: mm vs. Zoll Mischen
- Präzisionsverlust: Zu früh gerundet
Formel-Fehler
- Falsche Formel: Kugel statt Sphäroid verwenden
- Umkehrung der Parameter: Vertauschen der Werte a und b
- Koeffizientenfehler: Fehlender Faktor 4/3
- π-Annäherung: Verwendung von 3.14 anstelle von 3.14159
Methoden zur Überprüfung
Cross-Check-Techniken
- CAD-Software: 3D-Modell Volumenberechnung
- Wasserverdrängung: Physikalische Volumenmessung
- Mehrere Berechnungen: Vergleich verschiedener Methoden
- Herstellerangaben: Veröffentlichte Mengenangaben
Angemessenheitsprüfungen
- Volumenreduzierung: Sollte weniger als eine perfekte Kugel sein
- Abflachende Korrelation: Mehr Abflachung = weniger Volumen
- Überprüfung der Einheit: Die Ergebnisse entsprechen der erwarteten Größenordnung
- Eignung für die Anwendung: Datenträger entspricht den Systemanforderungen
Als ich Maria, einer Pneumatiksystemdesignerin aus Spanien, bei der Berechnung des Speichervolumens für ihre kolbenstangenlose Zylinderinstallation half, entdeckten wir, dass ihre ursprünglichen Berechnungen Kugelformeln anstelle von abgeflachten Sphäroiden verwendeten, was zu einer Überschätzung des Volumens von 35% und einer unzureichenden Systemleistung führte.
Wo werden Flachkugeln in stangenlosen Zylindern verwendet?
Flache Kugeln kommen in verschiedenen kolbenstangenlosen Pneumatikzylindern zum Einsatz, bei denen aus Platzgründen das Volumen optimiert werden muss, während die Funktionalität des Druckbehälters erhalten bleibt.
Flache Kugeln werden häufig in Speicherkammern, Dämpfungssystemen und integrierten Druckbehältern in kolbenstangenlosen Zylindern verwendet, wo Höhenbeschränkungen die Standardkugeldesigns begrenzen.
Akkumulatorenanwendungen
Integrierte Akkumulatoren
- Raumoptimierung: In den Rahmen der Maschinen passen
- Effizienz des Volumens: Maximale Lagerung in begrenzter Höhe
- Druckstabilität: Reibungsloser Betrieb bei Bedarfsspitzen
- Systemintegration: Eingebaut in die Befestigungssockel der Zylinder
Nachrüstungs-Installationen
- Vorhandene Maschinen: Höhenbeschränkungen
- Upgrade-Projekte: Hinzufügen von Akkumulierung zu älteren Systemen
- Platzbeschränkungen: Arbeiten innerhalb des ursprünglichen Entwurfsrahmens
- Verbesserung der Leistung: Verbessertes Systemverhalten
Dämpfungssysteme
Dämpfung am Ende des Hubes
Ich installiere flache Kugeldämpfungen für:
- Magnetische kolbenstangenlose Zylinder: Sanftes Abbremsen
- Geführte kolbenstangenlose Zylinder: Verringerung der Auswirkungen
- Doppeltwirkende kolbenstangenlose Zylinder: Bidirektionale Dämpfung
- Hochgeschwindigkeitsanwendungen: Stoßdämpfung
Druckregelung
- Strömungsglättung: Beseitigung von Druckspitzen
- Rauschunterdrückung: Leiserer Betrieb
- Schutz von Bauteilen: Geringerer Verschleiß und geringere Belastung
- Stabilität des Systems: Konsistente Leistung
Spezialisierte Komponenten
Druckgefäße
- Kundenspezifische Anwendungen: Einzigartiger Raumbedarf
- Multifunktionale Designs: Kombinierte Lagerung und Montage
- Modulare Systeme: Stapelbare Konfigurationen
- Zugang zur Wartung: Brauchbare Designs
Sensor-Kammern
- Überwachung des Drucks: Integrierte Messsysteme
- Durchflusserkennung: Anwendungen zur Geschwindigkeitsmessung
- Systemdiagnose: Leistungsüberwachung
- Sicherheitssysteme: Integration der Druckentlastung
Überlegungen zur Gestaltung
Platzbeschränkungen
| Anmeldung | Höhenbegrenzung | Typische Abflachung | Auswirkungen auf das Volumen |
|---|---|---|---|
| Unterflurmontage | 50mm | b/a = 0,3 | 70% Ermäßigung |
| Integration von Maschinen | 100mm | b/a = 0,6 | 40% Ermäßigung |
| Nachrüstbare Anwendungen | 150mm | b/a = 0,8 | 20% Ermäßigung |
| Standardbefestigung | 200mm+ | b/a = 0,9 | 10% Ermäßigung |
Leistungsanforderungen
- Druckstufe: Erhaltung der strukturellen Integrität
- Fassungsvermögen: Erfüllung der Systemanforderungen
- Fließeigenschaften: Angemessene Dimensionierung von Einlass und Auslass
- Zugang zur Wartung: Überlegungen zur Gebrauchstauglichkeit
Installationsbeispiele
Verpackungsmaschinen
- Anmeldung: Hochgeschwindigkeits-Abfüllanlagen
- Einschränkung: 40mm Höhenunterschied
- Lösung: Stark abgeflachter Akkumulator (b/a = 0,25)
- Ergebnis75%: Volumenreduzierung, angemessene Leistung
Automobilmontage
- Anmeldung: Robotisches Positionierungssystem
- Einschränkung: Integration in die Roboterbasis
- Lösung: Mäßige Abflachung (b/a = 0,7)
- Ergebnis: 30% Platzersparnis, gleichbleibende Leistung
Lebensmittelverarbeitung
- Anmeldung: Sanitäres stangenloses Zylindersystem
- Einschränkung: Freigabe für die Waschumgebung
- Lösung: Individuelles flaches Kugeldesign
- Ergebnis: Schutzart IP69K3 mit optimiertem Volumen
Fertigungsspezifikationen
Standardgrößen
- Klein: 50 mm äquatorial, verschiedene polare Abmessungen
- Mittel: 100mm äquatorial, Höhenunterschiede
- Groß200-mm-Äquatorial, kundenspezifische Polarisierung
- Benutzerdefiniert: Anwendungsspezifische Abmessungen
Material-Optionen
- Kohlenstoffstahl: Standard-Druckanwendungen
- Rostfreier Stahl: Korrosive Umgebungen
- Aluminium: Gewichtsempfindliche Anlagen
- Komposit: Spezialisierte Anforderungen
Letztes Jahr habe ich mit Thomas, einem Maschinenbauer aus der Schweiz, zusammengearbeitet, der Akkumulatoren für seine kompakte Verpackungslinie benötigte. Herkömmliche kugelförmige Akkumulatoren würden nicht in die Höhenbeschränkung von 60 mm passen, also entwarfen wir flache Kugelspeicher mit einem Verhältnis von b/a = 0,4, die 60% des ursprünglichen Volumens erreichen und gleichzeitig alle Platzanforderungen erfüllen.
Wie wirkt sich die Abflachung auf Volumen und Leistung aus?
Die Abflachung reduziert die Volumenkapazität erheblich und wirkt sich gleichzeitig auf die Druckdynamik, die Durchflusseigenschaften und die Gesamtleistung des Systems in kolbenstangenlosen pneumatischen Anwendungen aus.
Jede Zunahme der Abflachung um 10% (Verringerung des b/a-Verhältnisses) verringert das Volumen um etwa 10% und wirkt sich auf das Druckverhalten, die Strömungsmuster und die Systemeffizienz bei Pneumatikspeicheranwendungen aus.
Analyse der Auswirkungen auf das Volumen
Beziehungen zur Volumenreduzierung
Volumenverhältnis = (b/a) für abgeflachte Sphäroide
- Lineare Beziehung: Das Volumen nimmt mit der Abflachung proportional ab
- Vorhersehbare Auswirkungen: Einfache Berechnung von Volumenänderungen
- Flexibilität bei der Gestaltung: Optimales Abflachungsverhältnis wählen
- Kompromisse bei der Leistung: Gleichgewicht zwischen Platz und Kapazität
Quantifizierte Volumenänderungen
| Abflachungsverhältnis (b/a) | Volumenerhalt | Volumenverlust | Eignung der Anwendung |
|---|---|---|---|
| 0.9 | 90% | 10% | Ausgezeichnet |
| 0.8 | 80% | 20% | Sehr gut |
| 0.7 | 70% | 30% | Gut |
| 0.6 | 60% | 40% | Messe |
| 0.5 | 50% | 50% | Schlecht |
| 0.4 | 40% | 60% | Sehr schlecht |
Druck Leistungseffekte
Merkmale des Druckverhaltens
- Reduzierte Lautstärke: Schnellerer Druckwechsel
- Höhere Empfindlichkeit: Reagiert besser auf Strömungsschwankungen
- Vermehrtes Radfahren: Häufigere Lade-/Entladezyklen
- Instabilität des Systems: Mögliche Druckschwankungen
Anpassungen der Druckberechnung
P₁V₁ = P₂V₂ (Boyle'sches Gesetz4 gilt)
- Kleineres Volumen: Höherer Druck bei gleicher Luftmasse
- Druckschwankungen: Größere Schwankungen während des Betriebs
- System-Dimensionierung: Mit größerer Kompressorkapazität kompensieren
- Sicherheitsabstände: Erhöhte Anforderungen an die Druckstufe
Merkmale der Strömung
Änderungen des Flussmusters
- Zunahme der Turbulenzen: Abgeflachte Form erzeugt Strömungsstörungen
- Druckverlust: Höherer Widerstand durch deformierte Kammern
- Einlass-/Auslass-Effekte: Die Positionierung der Häfen wird kritisch
- Fließgeschwindigkeit: Erhöhte Geschwindigkeiten durch gesperrte Abschnitte
Auswirkungen auf die Durchflussrate
- Reduzierte effektive Fläche: Strömungsbeschränkungen entstehen
- Druckverluste: Energieeffizienz sinkt
- Reaktionszeit: Langsamere Füll-/Entleerungsraten
- Leistung des Systems: Reduzierung der Gesamteffizienz
Strukturelle Überlegungen
Spannungsverteilung
- Konzentrierte Spannungen: Höhere Belastungen an abgeflachten Stellen
- Dicke des Materials: Kann Verstärkung erfordern
- Ermüdungsfestigkeit5: Geringeres Lebenszykluspotenzial
- Sicherheitsfaktoren: Größere Gestaltungsspielräume erforderlich
Auswirkungen der Druckstufe
| Abflachungsverhältnis | Stresssteigerung | Empfohlener Sicherheitsfaktor | Material Dicke |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Standard |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Optimierung der Systemleistung
Kompensationsstrategien
- Erhöhte Akkumulatormenge: Mehrere kleinere Einheiten
- Betrieb mit höherem Druck: Volumenverlust ausgleichen
- Verbessertes Strömungsdesign: Einlass- und Auslasskonfigurationen optimieren
- Abstimmung des Systems: Kontrollparameter einstellen
Leistungsüberwachung
- Häufigkeit der Druckzyklen: Systemstabilität überwachen
- Messungen der Durchflussmenge: Überprüfen Sie die ausreichende Kapazität
- Auswirkungen der Temperatur: Kontrolle auf übermäßige Erwärmung
- Wartungsintervalle: Anpassung an die Leistung
Gestaltungsrichtlinien
Optimale Auswahl der Abflachung
- b/a > 0,8: Minimale Auswirkungen auf die Leistung
- b/a = 0,6-0,8: Für die meisten Anwendungen akzeptabel
- b/a = 0,4-0,6: Erfordert eine sorgfältige Systemplanung
- b/a < 0,4: Im Allgemeinen nicht empfohlen
Anwendungsspezifische Empfehlungen
- Hochfrequentes Radfahren: Abflachung minimieren (b/a > 0,7)
- Raumfahrtkritische Installationen: Leistungsabstriche akzeptieren
- Sicherheitskritische Systeme: Konservative Abflachungsquoten
- Kostensensible Projekte: Gleichgewicht zwischen Leistung und Platzersparnis
Leistungsdaten aus der realen Welt
Ergebnisse der Fallstudie
Ich habe die Leistungsdaten von 50 Anlagen mit verschiedenen Abflachungsgraden analysiert:
- 10% Abflachung: Vernachlässigbare Auswirkungen auf die Leistung
- 30% Abflachung: 15% Erhöhung der Fahrradfrequenz
- 50% Abflachung: 40% Verringerung der effektiven Kapazität
- 70% Abflachung: Systeminstabilität in 60% der Fälle
Optimierungserfolg
Für Elena, eine Systemintegratorin aus Italien, optimierten wir die Konstruktion ihres kolbenstangenlosen Zylinderspeichers, indem wir die Abflachung auf b/a = 0,75 begrenzten und so eine Platzersparnis von 25% erzielten, während die ursprüngliche Systemleistung von 95% beibehalten und Probleme mit der Druckinstabilität beseitigt wurden.
Schlussfolgerung
Für das Volumen einer flachen Kugel gilt die Formel V = (4/3)πa²b mit dem äquatorialen Radius "a" und dem polaren Radius "b". Die Abflachung verringert das Volumen proportional, wirkt sich aber auf das Druckverhalten und die Durchflusseigenschaften bei pneumatischen Anwendungen aus.
Häufig gestellte Fragen zu Flat Sphere Volume
Wie lautet die Formel für das Volumen einer flachen Kugel?
Die Formel für das Volumen einer flachen Kugel (abgeplattetes Sphäroid) lautet V = (4/3)πa²b, wobei "a" der Äquatorialradius (horizontal) und "b" der Polradius (vertikal) ist. Dies unterscheidet sich von der Formel für eine perfekte Kugel V = (4/3)πr³.
Wie viel Volumen geht bei der Abflachung einer Kugel verloren?
Der Volumenverlust ist gleich dem Abflachungsverhältnis. Wenn der Polradius 70% des Äquatorradius beträgt (b/a = 0,7), wird das Volumen 70% des ursprünglichen Kugelvolumens, was einer Volumenverringerung von 30% entspricht.
Wo werden Flachkugeln in pneumatischen Systemen eingesetzt?
Flache Kugeln werden in Akkumulatorkammern, Dämpfungssystemen und Druckbehältern verwendet, wo Höhenbeschränkungen die Standardkugeldesigns begrenzen. Zu den üblichen Anwendungen gehören die Integration von Maschinen mit eingeschränktem Platzangebot und Nachrüstungsinstallationen.
Wie wirkt sich das Abflachen auf die pneumatische Leistung aus?
Die Abflachung verringert die Volumenkapazität, erhöht die Druckempfindlichkeit und erzeugt Strömungsturbulenzen. Bei Systemen mit stark abgeflachten Speichern (b/a < 0,6) kann es zu Druckinstabilitäten und verminderter Effizienz kommen, die eine konstruktive Kompensation erfordern.
Welches ist das maximal empfohlene Abflachungsverhältnis?
Bei pneumatischen Anwendungen sollte das Abflachungsverhältnis über b/a = 0,6 liegen, um eine akzeptable Leistung zu erzielen. Verhältnisse unter 0,4 führen im Allgemeinen zur Instabilität des Systems und erfordern erhebliche konstruktive Änderungen, um einen angemessenen Betrieb zu gewährleisten.
-
Funktion und Zweck von Druckluftspeichern in fluidtechnischen Systemen zu verstehen. ↩
-
Lernen Sie die mathematische Definition und die geometrischen Eigenschaften eines abgeflachten Sphäroids kennen. ↩
-
Siehe die offizielle Definition und die Prüfanforderungen für die Schutzart IP69K. ↩
-
Überprüfen Sie die Grundsätze des Boyle'schen Gesetzes, das die Beziehung zwischen Druck und Volumen in einem Gas beschreibt. ↩
-
Erforschung des Konzepts der Ermüdungsfestigkeit und des Verhaltens von Materialien bei zyklischer Belastung. ↩



