
Haben Sie schon einmal mysteriöse Vibrationen in Ihren Pneumatikleitungen festgestellt? Oder unerklärliche Kraftschwankungen in Ihren Zylindern trotz stabilem Versorgungsdruck? Diese Phänomene sind nicht zufällig - sie sind das Ergebnis von Druckwellen, die sich in Ihrem System ausbreiten und Auswirkungen haben, die von geringfügigen Ineffizienzen bis hin zu katastrophalen Ausfällen reichen können.
Druckschwankungen in pneumatischen Systemen sind Wellenphänomene, die sich mit Geschwindigkeiten ausbreiten, die sich der Schallgeschwindigkeit1und erzeugen dynamische Effekte, einschließlich Resonanz, stehende Wellen2und Druckverstärkung. Das Verständnis dieser Schwankungen ist von entscheidender Bedeutung, denn sie können zur Ermüdung von Komponenten, zur Instabilität der Steuerung und Energieverluste von 10-25% in typischen Industriesystemen3.
Letzten Monat beriet ich ein Automobilmontagewerk in Tennessee, wo ein kritisches pneumatisches Klemmsystem trotz stabilen Versorgungsdrucks intermittierende Kraftschwankungen aufwies. Das Wartungsteam hatte Ventile, Regler und sogar das gesamte System ausgetauscht. Luftaufbereitungsanlage4 ohne Erfolg. Durch die Analyse der Druckwellendynamik - insbesondere der stehenden Wellenmuster in den Versorgungsleitungen - stellten wir fest, dass sie mit einer Frequenz arbeiteten, die destruktive Interferenzen am Zylinder verursachte. Eine einfache Anpassung der Leitungslänge beseitigte das Problem und ersparte dem Unternehmen wochenlange Produktionsverzögerungen. Ich möchte Ihnen zeigen, wie das Verständnis der Druckschwankungstheorie die Zuverlässigkeit Ihres Pneumatiksystems verbessern kann.
Inhaltsübersicht
- Wellenausbreitungsgeschwindigkeit: Wie schnell breiten sich Druckstörungen in Ihrem System aus?
- Verifizierung stehender Wellen: Wie können Resonanzfrequenzen Leistungsprobleme verursachen?
- Methoden zur Impulsdämpfung: Welche Techniken dämpfen die zerstörerischen Druckschwingungen wirksam?
- Schlussfolgerung
- FAQs über Druckschwankungen in pneumatischen Systemen
Wellenausbreitungsgeschwindigkeit: Wie schnell breiten sich Druckstörungen in Ihrem System aus?
Zu verstehen, wie schnell sich Druckstörungen in pneumatischen Systemen ausbreiten, ist von grundlegender Bedeutung für die Vorhersage und Kontrolle ihrer Auswirkungen. Die Ausbreitungsgeschwindigkeit bestimmt die Reaktionszeit des Systems, die Resonanzfrequenzen und das Potenzial für destruktive Störungen.
Druckwellen in pneumatischen Systemen breiten sich mit der Schallgeschwindigkeit im Gasmedium aus, die mit der Formel c = √(γRT) berechnet werden kann, wobei γ das spezifische Wärmeverhältnis, R die spezifische Gaskonstante und T die absolute Temperatur ist. Für Luft bei 20°C entspricht dies etwa 343 m/s, obwohl diese Geschwindigkeit durch Faktoren wie die Elastizität der Rohre, die Kompressibilität des Gases und die Strömungsbedingungen verändert wird.
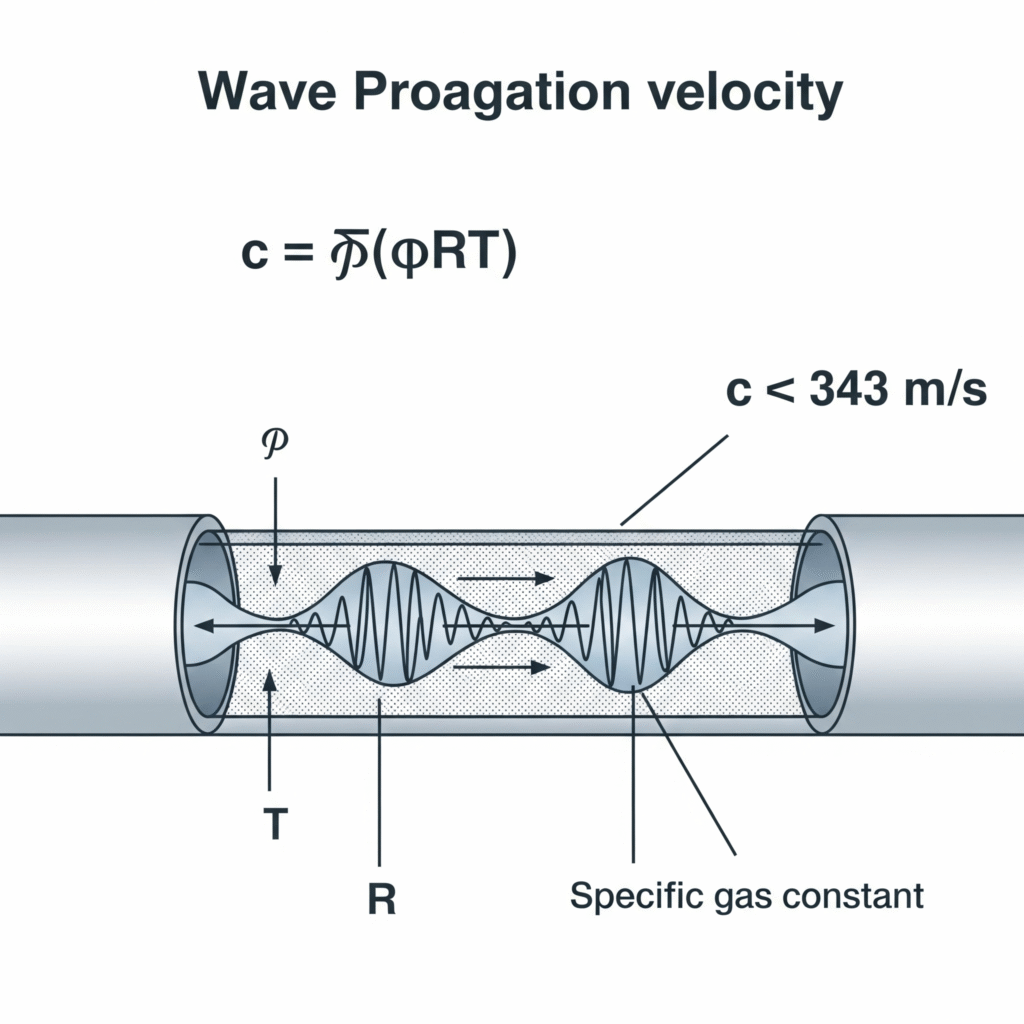
Vor kurzem half ich bei der Fehlersuche an einer Präzisionsmontagemaschine in der Schweiz, bei der pneumatische Greifer eine Verzögerung von 12 ms zwischen Aktivierung und Krafteinleitung aufwiesen - eine Ewigkeit in einer Hochgeschwindigkeitsproduktionsumgebung. Die Ingenieure waren von einer sofortigen Druckübertragung ausgegangen. Durch Messung der tatsächlichen Wellenausbreitungsgeschwindigkeit in ihrem System (328 m/s) und unter Berücksichtigung der 4 Meter langen Leitung berechneten wir eine theoretische Übertragungszeit von 12,2 ms - was fast genau der beobachteten Verzögerung entsprach. Durch die Verlegung der Ventile näher an die Aktuatoren wurde diese Verzögerung auf 3 ms reduziert und die Produktionsrate um 14% erhöht.
Grundlegende Gleichungen zur Wellengeschwindigkeit
Die grundlegende Gleichung für die Ausbreitungsgeschwindigkeit von Druckwellen in einem Gas lautet:
c = √(γRT)
Wo:
- c = Wellenausbreitungsgeschwindigkeit (m/s)
- γ = Spezifisches Wärmeverhältnis (1,4 für Luft)
- R = spezifische Gaskonstante (287 J/kg-K für Luft)
- T = Absolute Temperatur (K)
Für Luft bei 20°C (293K) ergibt dies:
c = √(1,4 × 287 × 293) = 343 m/s
Modifizierte Wellengeschwindigkeit in pneumatischen Leitungen
In realen pneumatischen Systemen wird die effektive Wellengeschwindigkeit durch die Elastizität der Rohre und andere Faktoren gemäß der Formel verändert:
c_eff = c / √(1 + (Dψ/Eh))
Wo:
- c_eff = Effektive Wellengeschwindigkeit (m/s)
- D = Rohrdurchmesser (m)
- ψ = Kompressibilitätsfaktor des Gases
- E = Elastizitätsmodul des Rohrmaterials (Pa)
- h = Wandstärke des Rohres (m)
Auswirkungen von Temperatur und Druck auf die Wellengeschwindigkeit
Die Wellengeschwindigkeit hängt von den Betriebsbedingungen ab:
| Temperatur | Druck | Wellengeschwindigkeit in Luft | Praktische Auswirkung |
|---|---|---|---|
| 0°C (273K) | 1 Bar | 331 m/s | Langsamere Reaktion in kalten Umgebungen |
| 20°C (293K) | 1 Bar | 343 m/s | Standard-Referenzbedingungen |
| 40°C (313K) | 1 Bar | 355 m/s | Schnellere Reaktion in warmen Umgebungen |
| 20°C (293K) | 6 bar | 343 m/s* | Druck hat nur minimale direkte Auswirkungen auf die Geschwindigkeit |
*Hinweis: Während die Grundwellengeschwindigkeit unabhängig vom Druck ist, kann die effektive Geschwindigkeit in realen Systemen durch druckbedingte Änderungen der Elastizität der Rohre und des Gasverhaltens beeinflusst werden.
Praktische Berechnung der Wellenausbreitungszeit
Für ein pneumatisches System mit:
- Leitungslänge (L): 5 Meter
- Betriebstemperatur: 20°C (c = 343 m/s)
- Material der Rohre: Polyurethan-Rohre (verändert die Geschwindigkeit um etwa 5%)
Die effektive Wellengeschwindigkeit wäre:
c_eff = 343 × 0,95 = 326 m/s
Und die Wellenausbreitungszeit wäre:
t = L/c_eff = 5/326 = 0,0153 Sekunden (15,3 Millisekunden)
Dies ist die Mindestzeit, die eine Druckänderung benötigt, um von einem Ende der Leitung zum anderen zu gelangen - ein kritischer Faktor bei Hochgeschwindigkeitsanwendungen.
Techniken zur Messung der Wellengeschwindigkeit
Zur Messung der tatsächlichen Wellengeschwindigkeit in pneumatischen Systemen können verschiedene Methoden verwendet werden:
Doppeldrucksensor-Methode
- Installieren Sie Drucksensoren in bekannten Abständen
- Erzeugen eines Druckimpulses (schnelle Ventilöffnung)
- Messung der Zeitverzögerung zwischen Druckanstieg an jedem Sensor
- Berechnung der Geschwindigkeit als Entfernung geteilt durch die Zeitverzögerung
Resonanzfrequenz-Methode
- Druckschwingungen in einem geschlossenen Rohr erzeugen
- Messung der Grundresonanzfrequenz (f)
- Berechnung der Geschwindigkeit mit c = 2Lf für ein Rohr mit geschlossenem Ende
- Überprüfung mit Oberwellen (ungerade Vielfache der Grundwelle)
Reflexionszeitpunktmethode
- Installieren Sie einen Drucksensor in der Nähe eines Ventils
- Erzeugen eines Druckimpulses durch schnelles Öffnen des Ventils
- Messung der Zeit zwischen Anfangsimpuls und reflektiertem Impuls
- Berechnung der Geschwindigkeit als 2L geteilt durch die Reflexionszeit
Fallstudie: Auswirkungen der Wellengeschwindigkeit auf das Systemverhalten
Für einen robotischen Endeffektor mit pneumatischen Greifern:
| Parameter | Originalentwurf (5m Zeilen) | Optimiertes Design (1m-Linien) | Verbesserung |
|---|---|---|---|
| Zeilenlänge | 5 Meter | 1 Meter | 80% Ermäßigung |
| Wellenausbreitungszeit | 15,3 ms | 3,1 ms | 12,2 ms schneller |
| Druckaufbauzeit | 28 ms | 9 ms | 19 ms schneller |
| Stabilität der Griffkraft | ±12% Abweichung | ±3%-Abweichung | 75% Verbesserung |
| Zykluszeit | 1,2 Sekunden | 0,95 Sekunden | 21% schneller |
| Produktionsrate | 3000 Teile/Stunde | 3780 Teile/Stunde | 26% Erhöhung |
Diese Fallstudie zeigt, wie das Verständnis und die Optimierung der Wellenausbreitung die Systemleistung erheblich beeinflussen können.
Verifizierung stehender Wellen: Wie können Resonanzfrequenzen Leistungsprobleme verursachen?
Stehende Wellen treten auf, wenn Druckwellen sich selbst reflektieren und überlagern, wodurch feste Muster von Druckknoten und -gegenknoten entstehen. Diese Resonanzphänomene können zu schwerwiegenden Leistungsproblemen in pneumatischen Systemen führen, wenn sie nicht richtig verstanden und gehandhabt werden.
Stehende Wellen in pneumatischen Systemen entstehen, wenn Druckwellen an Grenzflächen reflektiert werden und konstruktiv interferieren, wodurch Resonanzfrequenzen entstehen, bei denen Druckschwankungen verstärkt werden. Diese Resonanzen folgen der Formel f = nc/2L für geschlossene Rohre, wobei n die Oberwellenzahl, c die Wellengeschwindigkeit und L die Rohrlänge ist. Die experimentelle Überprüfung durch Drucksensoren, Beschleunigungsmesser und akustische Messungen bestätigt diese theoretischen Vorhersagen und liefert Anhaltspunkte für wirksame Minderungsstrategien.
Bei einem kürzlich durchgeführten Projekt mit einem Hersteller medizinischer Geräte in Massachusetts zeigte dessen pneumatisches Präzisionspositioniersystem bei bestimmten Betriebsfrequenzen mysteriöse Kraftschwankungen. Durch die Durchführung von Verifizierungstests mit stehenden Wellen konnten wir feststellen, dass die 2,1 Meter lange Versorgungsleitung eine Grundresonanz bei 81 Hz aufwies, die genau der Zyklusfrequenz des Stellantriebs entsprach. Diese Resonanz verstärkte die Druckschwankungen um 320%. Durch die Anpassung der Leitungslänge auf 1,8 Meter konnten wir die Resonanzfrequenz aus dem Betriebsbereich heraus verlagern und das Problem vollständig beseitigen, wodurch sich die Positioniergenauigkeit von ±0,8 mm auf ±0,15 mm verbesserte.
Stehende Welle - Grundlagen
Stehende Wellen entstehen, wenn einfallende und reflektierte Wellen sich überlagern und feste Muster von Druckknoten (minimale Fluktuation) und Anti-Knoten (maximale Fluktuation) bilden.
Die Resonanzfrequenzen für eine pneumatische Leitung hängen von den Randbedingungen ab:
Für eine Leitung mit geschlossenen Enden (am häufigsten in pneumatischen Systemen):
f = nc/2L
Wo:
- f = Resonanzfrequenz (Hz)
- n = Oberschwingungszahl (1, 2, 3, usw.)
- c = Wellengeschwindigkeit (m/s)
- L = Leitungslänge (m)
Für eine Leitung mit einem offenen Ende:
f = (2n-1)c/4L
Für eine Leitung, deren beide Enden offen sind (selten in der Pneumatik):
f = nc/2L
Experimentelle Überprüfungsmethoden
Mit verschiedenen Techniken können stehende Wellenmuster in pneumatischen Systemen überprüft werden:
Array mit mehreren Drucksensoren
- Installieren Sie in regelmäßigen Abständen Druckmessumformer entlang der Druckluftleitung
- Erregen Sie das System mit einem Frequenzsweep oder Impuls
- Aufzeichnung von Druckschwankungen an jedem Standort
- Abbildung der Druckamplitude in Abhängigkeit von der Position zur Identifizierung von Knoten und Anti-Knoten
- Vergleich von gemessenen Frequenzen mit theoretischen Vorhersagen
Akustische Korrelation
- Akustische Sensoren (Mikrofone) verwenden, um Geräusche aus Druckschwankungen zu erkennen
- Korrelieren Sie die Schallintensität mit der Betriebsfrequenz
- Erkennen von Spitzen in der Schallintensität, die den Resonanzfrequenzen entsprechen
- Überprüfen Sie, ob die Spitzenwerte bei den vorhergesagten Frequenzen auftreten.
Beschleunigungsmesser-Messungen
- Montage von Beschleunigungsaufnehmern an pneumatischen Leitungen und Komponenten
- Messung der Schwingungsamplitude über den gesamten Frequenzbereich
- Identifizierung von Resonanzspitzen im Schwingungsspektrum
- Korreliert mit den vorhergesagten Frequenzen der stehenden Wellen
Praktische Berechnung der Frequenz stehender Wellen
Für ein typisches pneumatisches System mit:
- Leitungslänge (L): 3 Meter
- Wellengeschwindigkeit (c): 343 m/s
- Konfiguration der geschlossenen Enden
Die grundlegende Resonanzfrequenz wäre:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
Und die Oberschwingungen würden sein:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Diese Frequenzen stellen potenzielle Problemstellen dar, an denen sich Druckschwankungen verstärken können.
Stehende Wellenmuster und ihre Auswirkungen
| Harmonische | Knoten/Antinode-Muster | Auswirkungen des Systems | Betroffene kritische Komponenten |
|---|---|---|---|
| Grundlegend (n=1) | Ein Druck-Antiknoten in der Mitte | Große Druckschwankungen in der Mitte der Linie | Inline-Komponenten, Armaturen |
| Zweite (n=2) | Zwei Anti-Knoten, Knoten in der Mitte | Druckschwankungen in der Nähe der Enden | Ventile, Stellantriebe, Regler |
| Dritter (n=3) | Drei Antinodes, zwei Nodes | Komplexes Druckmuster | Mehrere Systemkomponenten |
| Vierte (n=4) | Vier Antinodes, drei Nodes | Hochfrequente Schwingungen | Dichtungen, Kleinteile |
Experimentelle Verifizierung Fallstudie
Für ein pneumatisches Präzisionspositioniersystem mit unbeständiger Leistung:
| Parameter | Theoretische Vorhersage | Experimentelle Messung | Korrelation |
|---|---|---|---|
| Grundfrequenz | 81,2 Hz | 79,8 Hz | 98.3% |
| Zweite Harmonische | 162,4 Hz | 160,5 Hz | 98.8% |
| Dritte Harmonische | 243,6 Hz | 240,1 Hz | 98.6% |
| Druck-Verstärkung | 3:1 bei Resonanz (geschätzt) | 3,2:1 bei Resonanz (gemessen) | 93.8% |
| Knotenpunkte | 0, 1,05, 2,1 Meter | 0, 1,08, 2,1 Meter | 97.2% |
Diese Fallstudie zeigt die hervorragende Übereinstimmung zwischen theoretischen Vorhersagen und experimentellen Messungen von Stehwellenphänomenen.
Praktische Implikationen stehender Wellen
Stehende Wellen verursachen in pneumatischen Systemen mehrere erhebliche Probleme:
Druck-Verstärkung
- Schwankungen können bei Resonanz 3-5fach verstärkt werden
- Kann die Druckstufen der Komponenten überschreiten
- Erzeugt Kraftschwankungen in AktorenBauteil Ermüdung
- Hochfrequente Druckzyklen beschleunigen den Verschleiß der Dichtungen
- Vibrationen führen zur Lockerung von Armaturen und zu Leckagen
- Verkürzt die Lebensdauer des Systems in schweren Fällen um 30-70%Kontrolle der Instabilität
- Rückkopplungssysteme können bei Resonanzfrequenzen schwingen
- Positions- und Kraftkontrolle wird unberechenbar
- Kann selbstverstärkende Schwingungen erzeugenEnergieverluste
- Stehende Wellen stellen gefangene Energie dar
- Kann den Energieverbrauch um 10-30% erhöhen
- Reduziert die Gesamteffizienz des Systems
Methoden zur Impulsdämpfung: Welche Techniken dämpfen die zerstörerischen Druckschwingungen wirksam?
Die Beherrschung von Druckschwankungen ist für den zuverlässigen Betrieb von Pneumatiksystemen unerlässlich. Verschiedene Dämpfungsmethoden können eingesetzt werden, um problematische Druckschwankungen zu reduzieren oder zu beseitigen.
Die Dämpfung von Druckimpulsen in pneumatischen Systemen kann durch verschiedene Methoden erreicht werden: Volumenkammern, die Energie durch Gaskompression absorbieren, Drosselelemente, die durch viskose Effekte Dämpfung erzeugen, abgestimmte Resonatoren, die bestimmte Frequenzen auslöschen, und aktive Auslöschungssysteme, die Gegenimpulse erzeugen. Eine wirksame Dämpfung erfordert die Anpassung der Methode an den spezifischen Frequenzgehalt und die Amplitude der Druckschwankungen.
Kürzlich arbeitete ich mit einem Hersteller von Verpackungsanlagen in Illinois zusammen, dessen Hochgeschwindigkeits-Pneumatiksystem starke Druckschwankungen aufwies, die zu ungleichmäßigen Dichtungskräften führten. Die Ingenieure des Unternehmens hatten es ohne Erfolg mit einfachen Empfängertanks versucht. Durch eine detaillierte Druckimpulsanalyse konnten wir feststellen, dass das System mehrere Frequenzkomponenten aufwies, die unterschiedliche Dämpfungsansätze erforderten. Durch die Implementierung einer Hybridlösung, die eine Helmholtz-Resonator5 abgestimmt auf ihre dominante 112-Hz-Schwingung und eine Reihe von Drosselblenden, konnten wir die Druckschwankungen um 94% reduzieren und die Dichtungsunregelmäßigkeiten vollständig beseitigen.
Grundlegende Dämpfungsmechanismen
Zur Abschwächung von Druckimpulsen können verschiedene physikalische Mechanismen eingesetzt werden:
Volumenbasierte Abschwächung
Funktioniert durch die Kompressibilität von Gas:
- Bietet ein nachgiebiges Element, das die Druckenergie absorbiert
- Am wirksamsten bei niederfrequenten Schwankungen
- Einfache Implementierung mit minimalem Druckabfall
Einschränkungsbasierte Abschwächung
Funktioniert durch viskose Dissipation:
- Wandelt Druckenergie durch Reibung in Wärme um
- Wirksam in einem breiten Frequenzbereich
- Erzeugt permanenten Druckabfall
Resonatorgestützte Dämpfung
Funktioniert durch abgestimmte destruktive Interferenz:
- Löscht bestimmte Frequenzkomponenten
- Hochwirksam für gezielte Frequenzen
- Minimale Auswirkungen auf den stationären Fluss
Materialbedingte Dämpfung
Wirkt durch Wandflexibilität und Dämpfung:
- Absorption von Energie durch Wandverformung
- Bietet breitbandige Dämpfung
- Kann in bestehende Komponenten integriert werden
Konstruktionsprinzipien der Volumenkammer
Volumenkammern (Sammelbehälter) sind die gängigsten Dämpfungsvorrichtungen:
Die Wirksamkeit einer Volumenkammer hängt vom Verhältnis des Kammervolumens zum Leitungsvolumen ab:
Dämpfungsverhältnis = 1 + (Vc/Vl)
Wo:
- Vc = Kammervolumen
- Vl = Leitungsvolumen
Für die frequenzabhängige Analyse ist das Übersetzungsverhältnis:
TR = 1/√(1 + (ωVc/Zc)²)
Wo:
- ω = Winkelfrequenz (2πf)
- Zc = Charakteristische Impedanz der Leitung
Restriktives Element Dämpfung
Öffnungen, poröse Materialien und lange, enge Passagen erzeugen Dämpfung durch viskose Effekte:
Der Druckabfall über eine Drosselstelle ergibt sich wie folgt:
ΔP = k(ρv²/2)
Wo:
- k = Verlustkoeffizient
- ρ = Gasdichte
- v = Geschwindigkeit
Die gebotene Dämpfung steigt mit:
- Höhere Fließgeschwindigkeit
- Größere Länge der Beschränkung
- Kleinerer Durchgangsdurchmesser
- Gewundener Fließweg
Resonator-Dämpfungssysteme
Abgestimmte Resonatoren sorgen für eine gezielte Frequenzabschwächung:
Helmholtz-Resonator
Eine Volumenkammer mit einem engen Hals, die auf eine bestimmte Frequenz abgestimmt ist:
f = (c/2π)√(A/VL)
Wo:
- f = Resonanzfrequenz
- c = Schallgeschwindigkeit
- A = Querschnittsfläche des Halses
- V = Kammervolumen
- L = Effektive Halslänge
Viertelwellen-Resonator
Ein an einem Ende offenes Rohr von bestimmter Länge:
f = c/4L
Wo:
- L = Rohrlänge
Seitenkanal-Resonatoren
Mehrere abgestimmte Zweige für komplexe Frequenzinhalte:
- Jeder Zweig zielt auf eine bestimmte Frequenz ab
- Kann mehrere Oberschwingungen gleichzeitig behandeln
- Minimale Auswirkung auf den Hauptflussweg
Aktive Löschungssysteme
Fortschrittliche Systeme, die Gegenimpulse erzeugen:
Erfassungsphase
- Eingehende Druckwellen erkennen
- Analysieren Sie Frequenzinhalt und AmplitudeVerarbeitungsphase
- Berechnung des erforderlichen Annullierungssignals
- Berücksichtigung von Systemdynamik und VerzögerungenBetätigungsstufe
- Erzeugen von Gegendruckwellen
- Genaue Zeit für destruktive Interferenz
Vergleich der Dämpfungsleistung
| Methode | Niedrige Frequenz (<50 Hz) | Mittlere Frequenz (50-200 Hz) | Hochfrequenz (>200 Hz) | Druckabfall | Komplexität |
|---|---|---|---|---|---|
| Volumen Kammer | Ausgezeichnet (>90%) | Mäßig (40-70%) | Schlecht (<30%) | Sehr niedrig | Niedrig |
| Drosselblende | Schlecht (<30%) | Gut (60-80%) | Ausgezeichnet (>80%) | Hoch | Niedrig |
| Helmholtz-Resonator | Schlechte äußere Resonanz | Hervorragend bei Resonanz | Schlechte äußere Resonanz | Niedrig | Mittel |
| Viertelwellenrohr | Schlechte äußere Resonanz | Hervorragend bei Resonanz | Schlechte äußere Resonanz | Niedrig | Mittel |
| Mehrere Resonatoren | Mäßig (40-60%) | Ausgezeichnet (>80%) | Gut (60-80%) | Niedrig | Hoch |
| Aktive Annullierung | Ausgezeichnet (>90%) | Ausgezeichnet (>90%) | Gut (70-85%) | Keine | Sehr hoch |
| Hybride Systeme | Ausgezeichnet (>90%) | Ausgezeichnet (>90%) | Ausgezeichnet (>90%) | Mäßig | Hoch |
Praktische Umsetzung der Dämpfung
Für eine effektive Druckpulsdämpfung:
Charakterisieren Sie die Schwankungen
- Messung von Amplitude und Frequenzgehalt
- Identifizierung dominanter Frequenzen
- Bestimmen, ob Breitband oder bestimmte Frequenzen gedämpft werden müssenGeeignete Methoden auswählen
- Für niedrige Frequenzen: Volumen-Kammern
- Für bestimmte Frequenzen: Abgestimmte Resonatoren
- Für Breitbanddämpfung: Restriktionen oder hybride Ansätze
- Für kritische Anwendungen: Aktive LöschungOptimierung der Platzierung
- In der Nähe von Quellen, um eine Ausbreitung zu verhindern
- In der Nähe empfindlicher Komponenten, um sie zu schützen
- An strategischen Stellen, um stehende Wellenmuster zu brechenLeistung überprüfen
- Messung vor/nach Dämpfung
- Bestätigen Sie alle Betriebsbedingungen
- Sicherstellen, dass keine unbeabsichtigten Folgen auftreten
Fallstudie: Multimethoden-Dämpfung im Hochgeschwindigkeits-Packaging
Für ein pneumatisches Hochgeschwindigkeits-Dichtungssystem, das Druckschwankungen ausgesetzt ist:
| Parameter | Vor Abschwächung | Nach Volumen Kammer | Nach der Hybridlösung | Verbesserung |
|---|---|---|---|---|
| Niedrige Frequenz (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | 94% Ermäßigung |
| Mittlere Frequenz (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | 94% Ermäßigung |
| Hochfrequenz (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | 90% Ermäßigung |
| Siegelkraft-Variation | ±28% | ±22% | ±2,5% | 91% Verbesserung |
| Produktrückweisungsrate | 4.2% | 3.1% | 0.3% | 93% Ermäßigung |
| System-Effizienz | Basislinie | +4% | +12% | 12% Verbesserung |
Diese Fallstudie zeigt, wie ein gezielter, methodenübergreifender Ansatz zur Dämpfung die Systemleistung drastisch verbessern kann.
Fortgeschrittene Abschwächungstechniken
Für besonders anspruchsvolle Anwendungen:
Verteilte Abschwächung
Verwendung mehrerer kleinerer Geräte anstelle eines großen Geräts:
- Platziert die Dämpfung näher an Quellen und empfindlichen Komponenten
- bricht stehende Wellenmuster effektiver auf
- Bietet Redundanz und konsistentere Leistung
Frequenzselektive Dämpfung
Ausrichtung auf bestimmte problematische Frequenzen:
- Verwendet mehrere Resonatoren, die auf unterschiedliche Frequenzen abgestimmt sind
- Beibehaltung der gewünschten Systemreaktion bei gleichzeitiger Beseitigung von Problemen
- Minimiert die Auswirkungen auf die Gesamtleistung des Systems
Adaptive Systeme
Anpassung der Dämpfung an die Betriebsbedingungen:
- Verwendet Sensoren zur Überwachung von Druckschwankungen
- Passt die Dämpfungsparameter automatisch an
- Optimiert die Leistung bei unterschiedlichen Bedingungen
Schlussfolgerung
Das Verständnis der Druckschwankungstheorie - Wellenausbreitungsgeschwindigkeit, Verifizierung stehender Wellen und Impulsabschwächungsmethoden - bildet die Grundlage für eine zuverlässige und effiziente Konstruktion von Pneumatiksystemen. Durch die Anwendung dieser Prinzipien können Sie mysteriöse Leistungsprobleme beseitigen, die Lebensdauer von Komponenten verlängern und die Systemeffizienz verbessern, während Sie einen gleichmäßigen Betrieb unter allen Betriebsbedingungen sicherstellen.
FAQs über Druckschwankungen in pneumatischen Systemen
Wie wirken sich Druckschwankungen auf die Lebensdauer von Pneumatikkomponenten aus?
Druckschwankungen verkürzen die Lebensdauer von Bauteilen durch mehrere Mechanismen erheblich: Sie verursachen einen beschleunigten Dichtungsverschleiß durch Mikrobewegungen an den Dichtungsoberflächen; sie führen zu Materialermüdung bei Membranen und flexiblen Elementen durch wiederholte Belastungszyklen; sie fördern das Lösen von Gewindeverbindungen durch Vibrationen; und sie erzeugen örtliche Spannungskonzentrationen an geometrischen Übergängen. Systeme mit starken unkontrollierten Druckschwankungen weisen in der Regel eine 40-70% kürzere Lebensdauer der Komponenten auf als ordnungsgemäß gedämpfte Systeme, wobei Dichtungen und Membranen besonders anfällig sind.
Welcher Zusammenhang besteht zwischen Leitungslänge und Druckreaktionszeit in pneumatischen Systemen?
Die Leitungslänge wirkt sich direkt auf die Ansprechzeit des Drucks aus und folgt einer einfachen Beziehung: Die Ansprechzeit nimmt linear mit der Leitungslänge zu, und zwar mit einer Rate, die durch die Wellenausbreitungsgeschwindigkeit bestimmt wird. Bei Luft unter Standardbedingungen (Wellengeschwindigkeit ≈ 343 m/s) erhöht jeder Meter Leitung die Übertragungsverzögerung um etwa 2,9 Millisekunden. Die tatsächliche Druckaufbauzeit ist jedoch in der Regel 2-5 mal länger als die anfängliche Wellenübertragungszeit, da zum Druckausgleich mehrere Reflexionen erforderlich sind. Das bedeutet, dass eine 5-Meter-Leitung eine Wellenübertragungszeit von 14,5 ms, aber eine Druckaufbauzeit von 30-70 ms haben kann.
Wie kann ich feststellen, ob mein pneumatisches System resonante Druckschwankungen aufweist?
Resonante Druckschwankungen äußern sich in der Regel durch mehrere beobachtbare Symptome: Komponenten vibrieren bei bestimmten Betriebsfrequenzen, bei anderen nicht; die Systemleistung schwankt bei geringfügigen Änderungen der Betriebsbedingungen uneinheitlich; es gibt hörbares "Singen" oder "Pfeifen" von Pneumatikleitungen; Manometer zeigen oszillierende Messwerte an; und die Leistung der Aktoren (Geschwindigkeit, Kraft) schwankt zyklisch. Um eine Resonanz zu bestätigen, messen Sie den Druck an verschiedenen Punkten im System mit schnell ansprechenden Aufnehmern (Ansprechzeit <1ms) und achten Sie auf stehende Wellenmuster, bei denen die Druckamplitude mit der Position entlang der Leitung variiert.
Beeinflussen Druckschwankungen die Energieeffizienz in pneumatischen Systemen?
Druckschwankungen wirken sich erheblich auf die Energieeffizienz aus und verringern sie in der Regel um 10-25% durch verschiedene Mechanismen: Sie erhöhen die Leckageraten, indem sie höhere Spitzendrücke erzeugen; sie vergeuden Energie bei der zyklischen Kompression und Expansion; sie verursachen eine erhöhte Reibung in den Komponenten aufgrund von Vibrationen; und sie veranlassen die Betreiber häufig dazu, den Versorgungsdruck zu erhöhen, um Leistungsprobleme auszugleichen. Darüber hinaus wandeln die durch Druckschwankungen verursachten Turbulenzen und Strömungsablösungen nützliche Druckenergie in Abwärme um. Die richtige Dämpfung von Druckschwankungen kann die Systemeffizienz ohne weitere Änderungen um 5-15% verbessern.
Wie wirken sich Temperaturänderungen auf das Verhalten von Druckwellen in pneumatischen Systemen aus?
Die Temperatur wirkt sich durch mehrere Mechanismen erheblich auf das Verhalten von Druckwellen aus: Sie wirkt sich direkt auf die Wellenausbreitungsgeschwindigkeit aus (ca. +0,6 m/s pro °C-Anstieg); sie verändert die Gasdichte und -viskosität und damit die Dämpfungseigenschaften; sie verändert die elastischen Eigenschaften pneumatischer Leitungen und wirkt sich damit auf die Wellenreflexion und -übertragung aus; und sie verschiebt die Resonanzfrequenzen (ca. +0,17% pro °C). Diese Temperaturempfindlichkeit bedeutet, dass ein System, das bei 20 °C einwandfrei funktioniert, bei 40 °C problematische Resonanzen aufweisen kann oder dass Dämpfungsvorrichtungen, die auf Winterbedingungen abgestimmt sind, im Sommer unwirksam sein können.
-
Bietet eine detaillierte Erklärung der physikalischen Grundlagen der Schallgeschwindigkeit, ihrer Berechnung und der Faktoren, die sie beeinflussen. ↩
-
Bietet ein grundlegendes Verständnis der Phänomene stehender Wellen, einschließlich der Frage, wie sie durch Interferenz entstehen, und ihrer wichtigsten Merkmale wie Knoten und Anti-Knoten. ↩
-
Bietet Beweise und Industriestudien, die den typischen Bereich von Energieverlusten, die durch Ineffizienzen wie Druckschwankungen in pneumatischen Systemen verursacht werden, verifizieren. ↩
-
Erklärt die Komponenten und die Funktion einer Luftaufbereitungseinheit (FRL), die für die Aufrechterhaltung der Luftqualität in pneumatischen Systemen unerlässlich ist. ↩
-
Bietet eine eingehende Erläuterung der Prinzipien eines Helmholtz-Resonators, eines wichtigen Geräts zur gezielten Frequenzdämpfung in akustischen und flüssigen Systemen. ↩


