
¿Tiene problemas con velocidades incoherentes de los cilindros neumáticos o impactos inesperados al final de la carrera? Estos problemas comunes suelen deberse a una mala comprensión de la cinemática del pistón. Muchos ingenieros se centran únicamente en los requisitos de fuerza y pasan por alto los parámetros de movimiento críticos que determinan el rendimiento del sistema.
Cinemática del pistón1 afectan directamente al rendimiento del sistema neumático a través de las relaciones presión-velocidad, los límites de aceleración y los requisitos de amortiguación. Comprender estos principios permite a los ingenieros dimensionar correctamente los componentes, predecir los perfiles de movimiento reales y evitar fallos prematuros en los cilindros sin vástago y otros actuadores neumáticos.
En mis más de 15 años en Bepto trabajando con sistemas neumáticos, he visto innumerables casos en los que la comprensión de estos principios fundamentales ha ayudado a los clientes a resolver problemas persistentes de rendimiento y a prolongar la vida útil de los equipos entre 3 y 5 veces.
Índice
- ¿Qué presión se necesita realmente para un movimiento a velocidad constante?
- ¿Cómo se calcula la aceleración máxima posible en cilindros neumáticos?
- ¿Por qué es importante el tiempo de amortiguación y cómo se calcula?
- Conclusión
- Preguntas frecuentes sobre la cinemática de pistones en sistemas neumáticos
¿Qué presión se necesita realmente para un movimiento a velocidad constante?
Muchos ingenieros se limitan a aplicar la máxima presión disponible a sus sistemas neumáticos, pero este planteamiento es ineficaz y puede provocar sacudidas, desgaste excesivo y derroche de energía.
La presión necesaria para el movimiento a velocidad constante en un cilindro neumático se calcula utilizando P = (F + Fr)/A, donde P es la presión, F es la fuerza de carga externa, Fr es la resistencia a la fricción y A es el área del pistón. Este cálculo garantiza un funcionamiento suave y eficaz sin una presión excesiva que desperdicia energía y acelera el desgaste de los componentes.
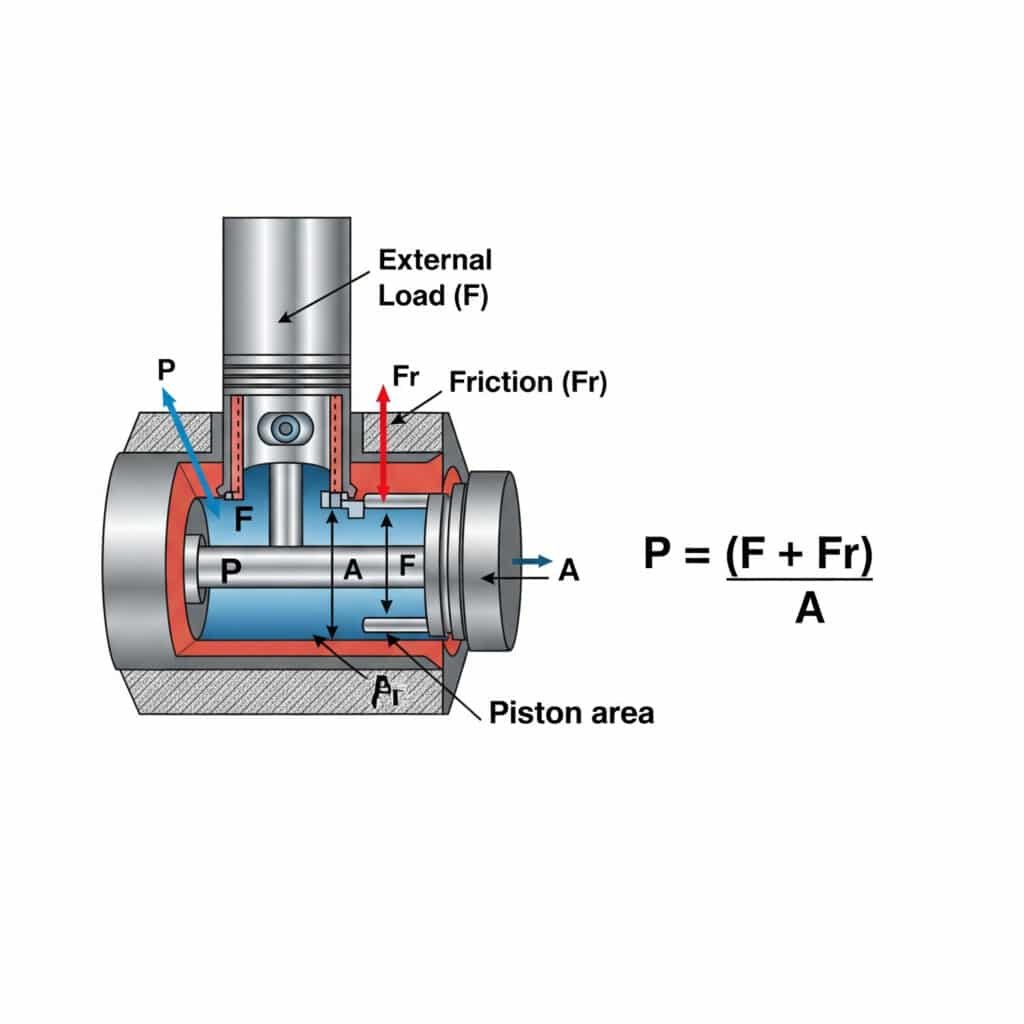
Comprender los requisitos de presión para el movimiento a velocidad constante tiene implicaciones prácticas para el diseño y el funcionamiento del sistema. Permítanme desglosarlo en ideas prácticas.
Factores que afectan a los requisitos de presión para velocidad constante
La presión necesaria para mantener una velocidad constante depende de varios factores:
| Factor | Impacto en la presión necesaria | Consideraciones prácticas |
|---|---|---|
| Carga externa | Relación lineal directa | Varía según la orientación y las fuerzas externas |
| Fricción | Aumenta la presión necesaria | Cambios con el desgaste de las juntas y la lubricación |
| Área del pistón | Inversamente proporcional | Mayor diámetro = menor presión requerida |
| Restricciones del suministro de aire | Caídas de presión en líneas/válvulas | Tamaño de los componentes para una caída de presión mínima |
| Contrapresión | Se opone a la moción | Considerar la capacidad del caudal de escape |
Cálculo de la presión mínima para un movimiento estable
Determinar la presión mínima necesaria para un movimiento estable:
- Calcular la fuerza necesaria para vencer la carga externa
- Añadir la fuerza de fricción (normalmente 3-20% de fuerza máxima).
- Dividir por el área efectiva del pistón
- Añade un factor de estabilidad (normalmente 10-30%)
Por ejemplo, en un cilindro sin vástago de 40 mm de diámetro con una carga de 10 kg y un rozamiento de 15%:
| Parámetro | Cálculo | Resultado |
|---|---|---|
| Fuerza de carga | 10kg × 9,81m/s² | 98.1N |
| Fuerza de fricción | 15% de fuerza máxima a 6 bar | ~45N |
| Fuerza total | 98,1N + 45N | 143.1N |
| Área del pistón | π × (0,02m)² | 0.00126m² |
| Presión mínima | 143,1N ÷ 0,00126m² | 113.571 Pa (1,14 bar) |
| Con 20% Factor de estabilidad | 1,14 bar × 1,2 | 1,37 bar |
Aplicación real: Ahorro de energía mediante la optimización de la presión
El año pasado trabajé con Robert, un ingeniero de producción de una fábrica de muebles de Michigan. Su línea de montaje automatizada utilizaba cilindros sin vástago que funcionaban a la máxima presión de suministro de 6 bares, independientemente de la carga.
Tras analizar su aplicación, determinamos que la mayoría de los movimientos sólo requerían entre 2,5 y 3 bares para un funcionamiento estable. Instalando reguladores de presión proporcionalesredujimos el consumo de aire en 40% manteniendo el mismo tiempo de ciclo. Esto supuso un ahorro de aproximadamente $12.000 anuales en costes energéticos, al tiempo que se reducía el desgaste de las juntas y se ampliaban los intervalos de mantenimiento.
Relación velocidad-presión en sistemas reales
En la práctica, la relación entre presión y velocidad no es perfectamente lineal debido a:
- Restricciones de caudal: El tamaño de las válvulas y los orificios influye en la velocidad máxima alcanzable
- Efectos de compresibilidad: El aire es compresible, lo que provoca retrasos en la aceleración
- Fenómenos de adherencia y deslizamiento: Las características de la fricción cambian con la velocidad
- Efectos inerciales: La aceleración de la masa requiere una fuerza/presión adicional
¿Cómo se calcula la aceleración máxima posible en cilindros neumáticos?
Comprender los límites de aceleración es crucial para evitar choques excesivos, vibraciones y fallos prematuros de los componentes en los sistemas neumáticos.
La aceleración máxima posible en un cilindro neumático se calcula mediante a = (P × A - F - Fr)/m, donde a es la aceleración, P es la presión, A es el área del pistón, F es la carga externa, Fr es la resistencia al rozamiento y m es la masa en movimiento. Esta ecuación define los límites físicos de la rapidez con que un actuador neumático puede iniciar o detener el movimiento.
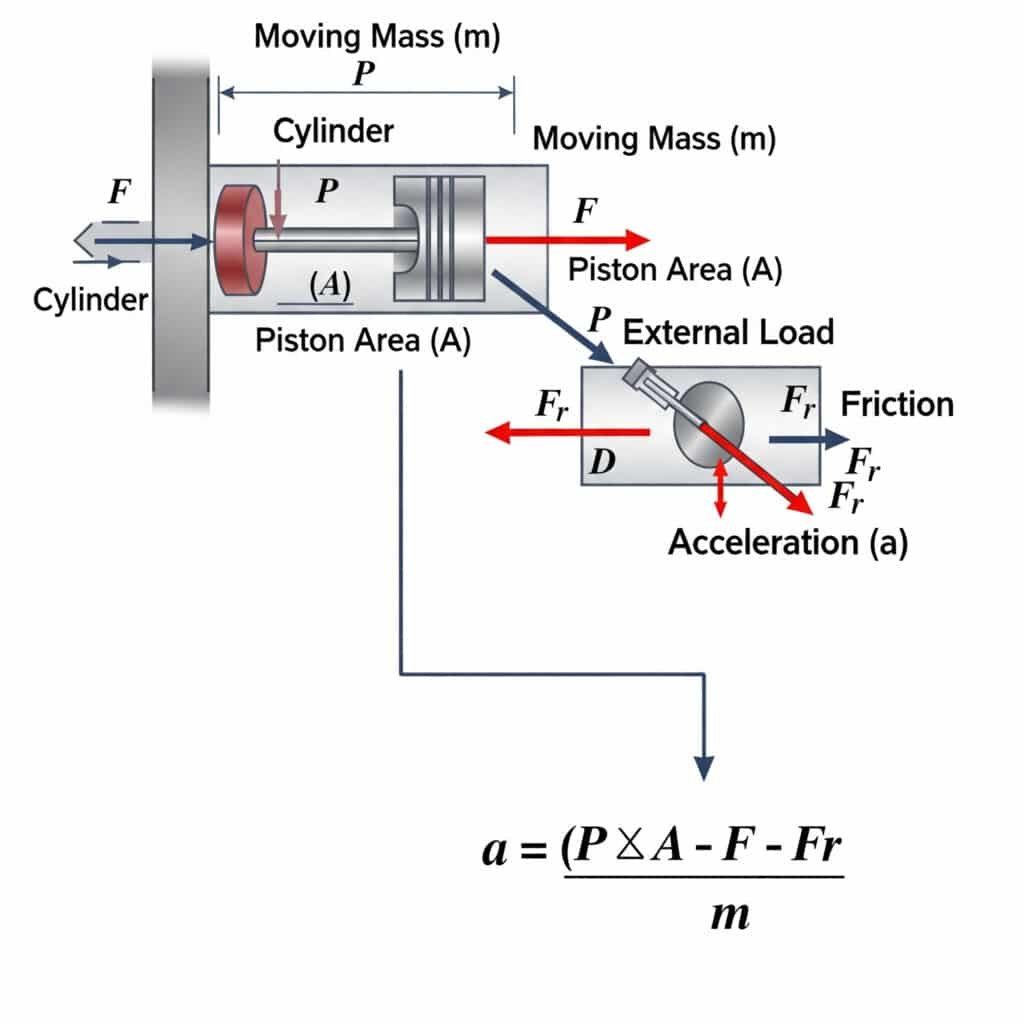
Los límites teóricos de aceleración tienen importantes implicaciones prácticas para el diseño de sistemas y la selección de componentes.
Derivación de la ecuación límite de aceleración
La ecuación del límite de aceleración procede de Segunda ley de Newton2 (F = ma):
- La fuerza neta disponible para la aceleración es Fnet = Fpresión - Fcarga - Fricción
- Fpresión = P × A
- Por tanto: a = Fnet/m = (P × A - F - Fr)/m
Límites prácticos de aceleración para distintos tipos de cilindros
Los diferentes diseños de cilindros tienen diferentes límites prácticos de aceleración:
| Tipo de cilindro | Aceleración máxima típica | Factores limitantes |
|---|---|---|
| Cilindro de vástago normalizado | 10-15 m/s² | Pandeo del vástago, cargas sobre los cojinetes |
| Cilindro sin vástago (magnético) | 8-12 m/s | Fuerza de acoplamiento magnético |
| Cilindro sin vástago (mecánico) | 15-25 m/s | Diseño de junta/rodamiento, fricción interna |
| Cilindro de guía | 20-30 m/s | Rigidez del sistema de guías, capacidad portante |
| Cilindro de impacto | 50-100+ m/s | Especialmente diseñado para altas aceleraciones |
Consideraciones sobre la masa en los cálculos de aceleración
Al calcular la aceleración, es fundamental incluir todas las masas en movimiento:
- Conjunto pistón: Incluye pistón, juntas y elementos de conexión
- Masa de carga: Carga externa que se desplaza
- Masa efectiva de aire en movimiento: A menudo insignificante, pero relevante en aplicaciones de alta velocidad.
- Masa añadida debido a los componentes de montaje: Soportes, sensores, etc.
Una vez ayudé a un cliente francés que sufría fallos misteriosos en su sistema de cilindros sin vástago. El cilindro estaba dimensionado correctamente para la carga de 15 kg indicada, pero fallaba sistemáticamente tras unos pocos miles de ciclos.
Tras investigar, descubrimos que no había tenido en cuenta los 12 kg de masa de la placa de montaje y los accesorios. La masa real en movimiento era casi el doble de lo que había calculado, lo que provocaba fuerzas de aceleración que superaban los límites de diseño del cilindro. Tras cambiar a un cilindro más grande, los fallos cesaron por completo.
Métodos de control de la aceleración
Para controlar la aceleración dentro de límites seguros:
- Válvulas reguladoras de caudal: Limitar el caudal durante el movimiento inicial
- Válvulas proporcionales: Proporciona un aumento controlado de la presión
- Aceleración multietapa: Utilizar aumentos de presión escalonados
- Amortiguación mecánica: Añadir amortiguadores externos
- Control electrónico: Utilice sistemas servoneumáticos3 con retroalimentación de aceleración
¿Por qué es importante el tiempo de amortiguación y cómo se calcula?
Una amortiguación adecuada al final de la carrera es esencial para evitar daños por impacto, reducir el ruido y prolongar la vida útil de los cilindros neumáticos. Comprender el tiempo de amortiguación ayuda a los ingenieros a diseñar sistemas que equilibren el tiempo de ciclo con la longevidad de los componentes.
El tiempo de amortiguación en los cilindros neumáticos se calcula mediante la ecuación t = √(2s/a), donde t es el tiempo, s es la longitud de la carrera de amortiguación y a es la deceleración. Este tiempo representa el tiempo que se tarda en decelerar con seguridad la masa en movimiento antes del impacto, lo que es crítico para evitar daños en el cilindro y los componentes acoplados.

Exploremos los aspectos prácticos del cálculo del tiempo de amortiguación y sus implicaciones para el diseño del sistema.
La física de la amortiguación neumática
Amortiguación neumática funciona mediante una compresión de aire controlada y un escape restringido:
- A medida que el pistón entra en la cámara de amortiguación, la trayectoria de escape se restringe
- El aire atrapado se comprime, creando una contrapresión creciente
- Esta contrapresión crea una fuerza contraria que desacelera el pistón
- El perfil de deceleración depende del diseño del cojín y del ajuste
Cálculo del tiempo óptimo de amortiguación
El tiempo de amortiguación óptimo equilibra la prevención de impactos con la eficiencia del tiempo de ciclo:
| Parámetro | Fórmula | Ejemplo |
|---|---|---|
| Distancia de amortiguación | Basado en el diseño del cilindro | 15 mm (típico para diámetro interior de 40 mm) |
| Desaceleración requerida | a = v²/(2s) | Para v=0,5m/s, s=15mm: a = 8,33m/s². |
| Tiempo de amortiguación | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Aumento de la presión | P = P₀(V₀/V)^γ | Depende de la geometría de la cámara del cojín |
Factores que afectan al rendimiento de la amortiguación
Varios factores influyen en el rendimiento real de la amortiguación:
- Diseño de junta amortiguadora: Afecta a las fugas de aire durante la amortiguación
- Ajuste de la válvula de aguja: Controla la tasa de restricción de escape
- Masa en movimiento: Las cargas más pesadas requieren más tiempo de amortiguación
- Velocidad de aproximación: A mayor velocidad, mayor distancia entre cojines
- Presión de funcionamiento: Afecta a la contrafuerza máxima disponible
Tipos de amortiguación y sus aplicaciones
Diferentes mecanismos de amortiguación son apropiados para diferentes aplicaciones:
| Tipo de amortiguación | Características | Mejores aplicaciones |
|---|---|---|
| Amortiguación fija | Simple, no ajustable | Cargas ligeras, funcionamiento constante |
| Amortiguación ajustable | Sintonizable con válvulas de aguja | Cargas variables, aplicaciones flexibles |
| Amortiguación autoajustable | Se adapta a diferentes condiciones | Cambio de velocidades y cargas |
| Amortiguadores externos | Alta absorción de energía | Cargas pesadas, altas velocidades |
| Amortiguación electrónica | Desaceleración controlada con precisión | Sistemas servoneumáticos |
Caso práctico: Optimización de la amortiguación en aplicaciones de ciclos altos
Hace poco trabajé con Thomas, ingeniero de diseño de un fabricante de componentes de automoción de Alemania. Su línea de montaje utilizaba cilindros sin vástago que funcionaban a 45 ciclos por minuto, pero sufría frecuentes fallos en las juntas y daños en los soportes de montaje.
El análisis reveló que el tiempo de amortiguación era demasiado corto para la masa en movimiento, lo que provocaba fuerzas de impacto de casi 3G en cada extremo de la carrera. Aumentando la carrera de amortiguación de 12 mm a 20 mm y optimizando los ajustes de la válvula de aguja, ampliamos el tiempo de amortiguación de 0,04 s a 0,07 s.
Este cambio aparentemente pequeño redujo las fuerzas de impacto en más de 60%, eliminó por completo los daños en los soportes y prolongó la vida útil de las juntas de 3 meses a más de un año, todo ello manteniendo el tiempo de ciclo requerido.
Procedimiento práctico de ajuste de la amortiguación
Para un rendimiento óptimo de la amortiguación en cilindros sin vástago:
- Empezar con las válvulas de cojín completamente abiertas (restricción mínima)
- Cierre gradualmente la válvula de amortiguación hasta conseguir una deceleración suave
- Prueba con cargas mínimas y máximas previstas
- Verificar el rendimiento de la amortiguación en toda la gama de velocidades
- Escucha los sonidos de impacto que indican una amortiguación insuficiente
- Mida el tiempo de deceleración real para confirmar los cálculos
Conclusión
Comprender los principios de la cinemática del pistón -desde los requisitos de presión para una velocidad constante hasta los límites de aceleración y los cálculos del tiempo de amortiguación- es esencial para diseñar sistemas neumáticos eficientes y fiables. Si aplica estos principios a sus aplicaciones de cilindros sin vástago, podrá optimizar el rendimiento, reducir el consumo de energía y prolongar considerablemente la vida útil de los componentes.
Preguntas frecuentes sobre la cinemática de pistones en sistemas neumáticos
¿Qué presión necesito para una velocidad de cilindro determinada?
La presión necesaria depende de la carga, la fricción y el área del cilindro. Calcúlala utilizando P = (F + Fr)/A, donde F es la fuerza de carga externa, Fr es la resistencia al rozamiento y A es el área del pistón. Para un cilindro sin vástago típico que desplace una carga de 10 kg horizontalmente, necesitarás aproximadamente 1,5-2 bar para un movimiento estable a velocidades moderadas.
¿A qué velocidad puede acelerar un cilindro neumático?
La aceleración máxima de un cilindro neumático se calcula mediante a = (P × A - F - Fr)/m. Los cilindros sin vástago típicos pueden alcanzar una aceleración de 10-25 m/s² dependiendo del diseño. Esto se traduce en alcanzar una velocidad de 0,5 m/s en aproximadamente 20-50 milisegundos en condiciones óptimas.
¿Qué factores limitan la velocidad máxima de un cilindro sin vástago?
La velocidad máxima está limitada por la capacidad de caudal de la válvula, el volumen de suministro de aire, el tamaño del puerto, la capacidad de amortiguación y el diseño de la junta. La mayoría de los cilindros sin vástago estándar están diseñados para velocidades máximas de 0,8-1,5 m/s, aunque los diseños especializados de alta velocidad pueden alcanzar 2-3 m/s.
¿Cómo calculo la amortiguación adecuada para mi aplicación?
Calcule la amortiguación adecuada determinando la energía cinética (KE = ½mv²) de su carga en movimiento y asegurándose de que su sistema de amortiguación puede absorber esta energía. El tiempo de amortiguación debe calcularse utilizando t = √(2s/a), donde s es la distancia de amortiguación y a es la velocidad de deceleración deseada.
¿Qué ocurre si mi cilindro neumático acelera demasiado deprisa?
Una aceleración excesiva puede provocar tensiones mecánicas en los componentes de montaje, desgaste prematuro de las juntas, aumento de las vibraciones y el ruido, posibles desplazamientos o daños de la carga y reducción de la precisión del sistema. También puede provocar movimientos bruscos que afectan a la calidad del producto en aplicaciones de precisión.
¿Cómo afecta la orientación de la carga a la presión necesaria para el movimiento?
La orientación de la carga influye significativamente en los requisitos de presión. Las cargas verticales que se mueven contra la gravedad requieren una presión adicional para superar la fuerza gravitatoria (P = F/A + Fg/A + Fr/A). Las cargas horizontales sólo necesitan vencer la fricción y la inercia. Las cargas inclinadas se sitúan entre estos extremos en función del seno del ángulo.
-
Proporciona una explicación básica de la cinemática, la rama de la mecánica que describe el movimiento de los objetos sin tener en cuenta las fuerzas que causan el movimiento.
señal de entrada electrónica, lo que permite un control neumático avanzado. ↩ -
Detalla la Segunda Ley de Newton (F=ma), el principio fundamental de la física que relaciona la fuerza que actúa sobre un objeto con su masa y aceleración, y que constituye la base de todos los cálculos dinámicos. ↩
-
Describe la servoneumática, una tecnología de control avanzada que combina la potencia de la neumática con la precisión del control electrónico en bucle cerrado para lograr perfiles de posicionamiento y movimiento de gran precisión. ↩


