La pesadilla de todo ingeniero de mantenimiento es un fallo inesperado de los equipos. Cuando las máquinas vibran a su frecuencia natural, pueden producirse daños catastróficos en cuestión de minutos. He visto cómo este problema costaba a las empresas miles de horas de inactividad.
Resonancia vibratoria1 se produce cuando una fuerza externa coincide con la frecuencia natural de un sistema, provocando oscilaciones amplificadas que pueden dañar los equipos. Comprender y controlar este fenómeno es esencial para prevenir averías y prolongar la vida útil de la maquinaria.
Permítanme contarles una anécdota. El año pasado, un cliente alemán me llamó asustado. Su línea de producción se había parado porque un cilindro sin vástago vibraba violentamente. ¿El problema? La resonancia. Al final de este artículo, sabrás cómo identificar y prevenir problemas similares en tus sistemas.
Índice
- Fórmula de frecuencia natural: ¿Cómo puede calcular los puntos vulnerables de su sistema?
- Modelo masa-muelle: ¿Por qué es tan valioso este enfoque simplificado?
- Optimización de la relación de amortiguación: ¿Qué experimentos dan mejores resultados?
- Conclusión
- Preguntas frecuentes sobre la resonancia vibratoria
Fórmula de frecuencia natural: ¿Cómo puede calcular los puntos vulnerables de su sistema?
Conocer la frecuencia natural de su equipo es el primer paso para evitar problemas de resonancia. Este valor crítico determina cuándo su sistema es más vulnerable a los problemas de vibración.
En frecuencia natural2 (fn) de un sistema puede calcularse mediante la fórmula: fn = (1/2π) × √(k/m), donde k es el coeficiente de rigidez y m es la masa. Este cálculo revela la frecuencia a la que resonará el sistema si es excitado por fuerzas externas coincidentes.
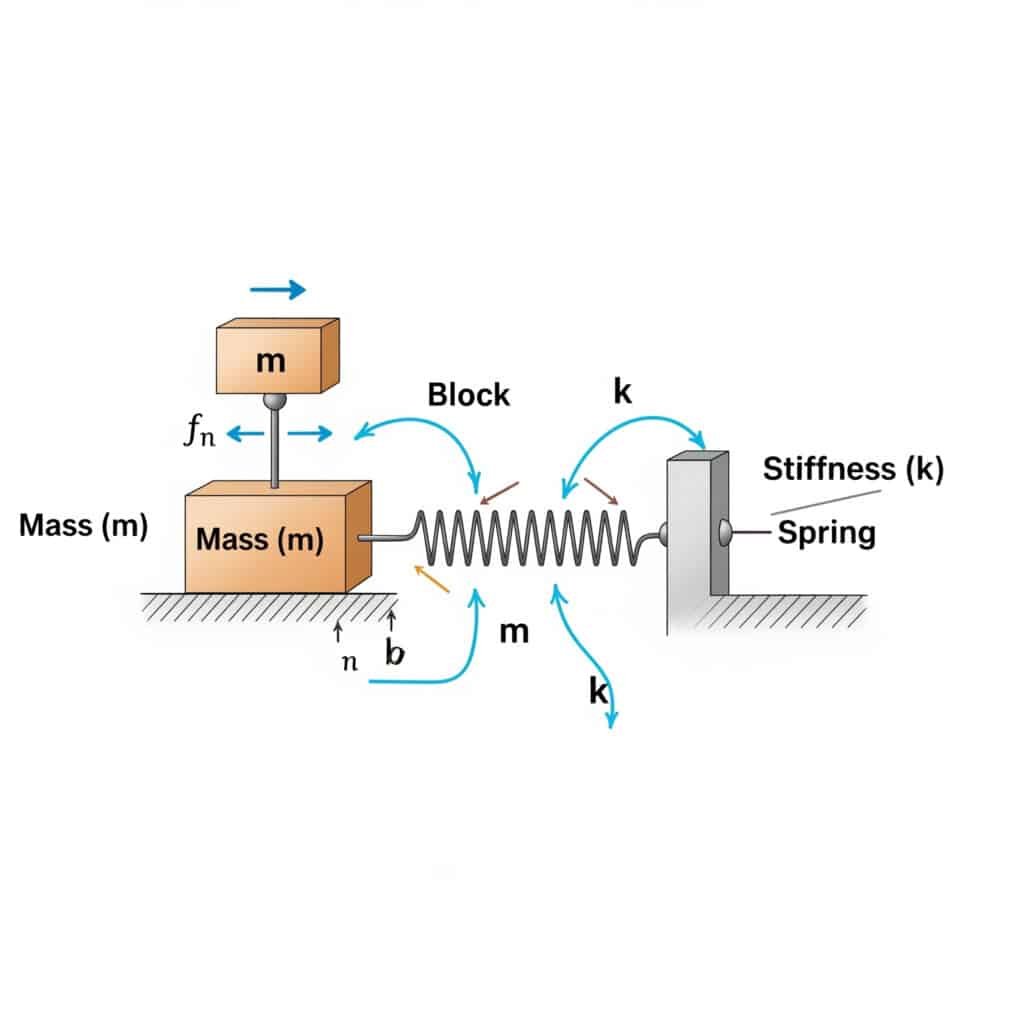
Cuando visité una fábrica en Suiza, me di cuenta de que sus cilindros neumáticos sin vástago fallaban prematuramente. El equipo de mantenimiento no había calculado la frecuencia natural del sistema. Tras aplicar esta fórmula, descubrimos que la velocidad de funcionamiento se acercaba peligrosamente a la frecuencia natural del sistema.
Aplicaciones prácticas del cálculo de la frecuencia natural
La fórmula de la frecuencia natural no es sólo teórica, sino que tiene aplicaciones directas en diversos entornos industriales:
- Selección de equipos: Elección de componentes con frecuencias naturales alejadas de sus condiciones de funcionamiento
- Mantenimiento preventivo: Programación de inspecciones basadas en perfiles de riesgo de vibración
- Solución de problemas: Identificar la causa de vibraciones inesperadas
Valores comunes de frecuencia natural para componentes industriales
| Componente | Frecuencia natural típica (Hz) |
|---|---|
| Cilindros sin vástago | 10-50 Hz |
| Soportes de montaje | 20-100 Hz |
| Estructuras de apoyo | 5-30 Hz |
| Válvulas de control | 40-200 Hz |
Factores críticos que afectan a la frecuencia natural
El cálculo de la frecuencia natural parece sencillo, pero varios factores pueden complicar las aplicaciones en el mundo real:
- Distribución no uniforme de la masa: La mayoría de los componentes industriales no tienen la masa perfectamente distribuida
- Rigidez variable: Los componentes pueden tener distinta rigidez en distintas direcciones
- Puntos de conexión: La forma en que se montan los componentes afecta significativamente a sus características de vibración
- Efectos de la temperatura: Tanto la masa como la rigidez pueden variar con la temperatura.
Modelo masa-muelle: ¿Por qué es tan valioso este enfoque simplificado?
El modelo masa-resorte proporciona un marco intuitivo para comprender sistemas de vibración complejos. Reduce la maquinaria complicada a elementos básicos que los ingenieros pueden analizar fácilmente.
En modelo masa-muelle3 simplifica el análisis de vibraciones representando los sistemas mecánicos como masas discretas conectadas por muelles. Este enfoque permite a los ingenieros predecir el comportamiento del sistema, identificar posibles problemas de resonancia y desarrollar soluciones eficaces sin necesidad de recurrir a matemáticas complejas.
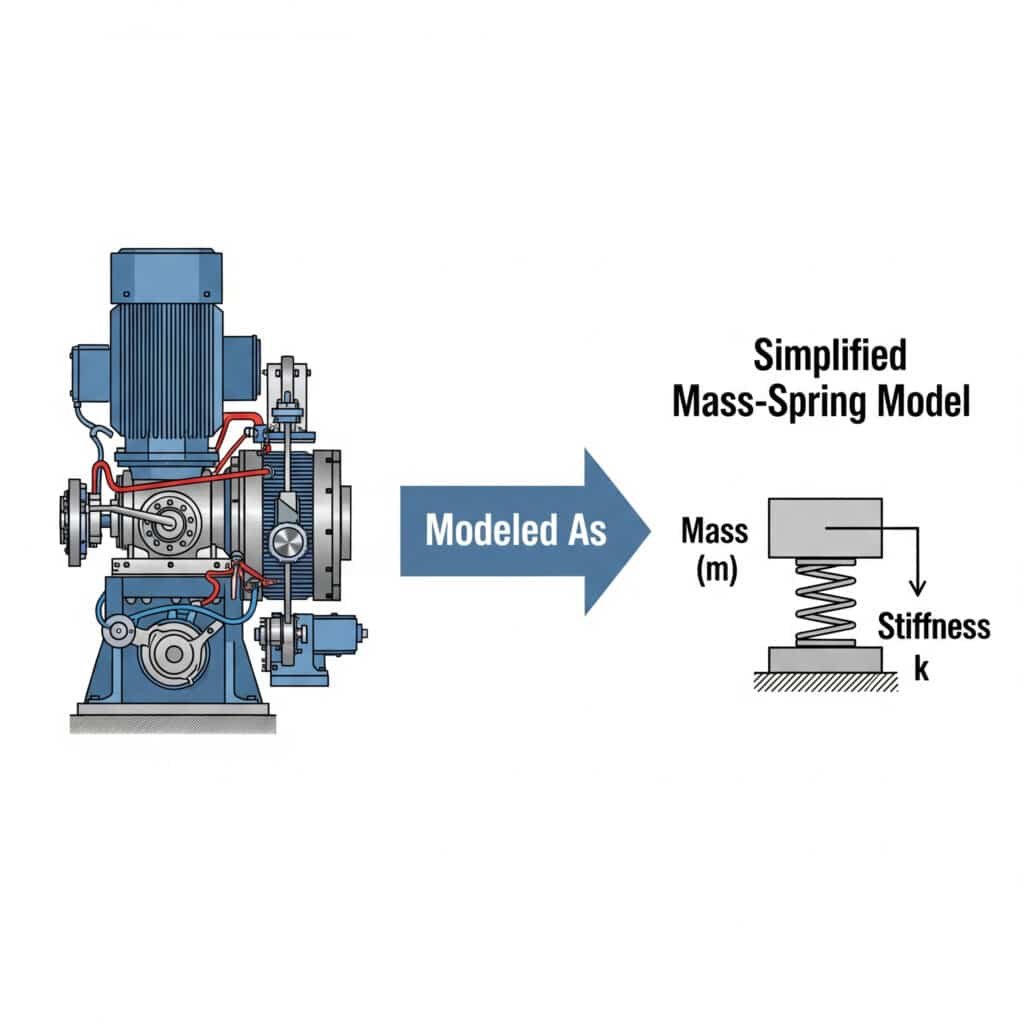
Recuerdo que trabajé con un fabricante de piezas de automóvil de Michigan que no entendía por qué fallaban sus cilindros sin vástago guiados. Al modelar su sistema como una simple disposición masa-resorte, identificamos que los soportes de montaje actuaban como resortes no intencionados, creando una condición de resonancia.
Conversión de sistemas reales en modelos masa-muelle
Para aplicar este enfoque a su equipo:
- Identificar las masas clave: Determinar qué componentes aportan un peso significativo
- Localizar los elementos de muelle: Encuentra componentes que almacenen y liberen energía (muelles reales, soportes flexibles, etc.)
- Mapa de conexiones: Documentar cómo interactúan las masas y los muelles
- Simplifique: Combinar elementos similares para crear un modelo manejable
Tipos de sistemas Mass-Spring
| Tipo de sistema | Descripción | Aplicaciones comunes |
|---|---|---|
| DOF único | Una masa con un muelle | Cilindros neumáticos simples |
| Multi-DOF | Múltiples masas con múltiples muelles | Maquinaria compleja con múltiples componentes |
| Continuo | DOF infinitos (requiere un análisis diferente) | Vigas, placas y corazas |
Consideraciones avanzadas sobre modelado
Aunque el modelo básico masa-resorte es valioso, varias mejoras lo hacen más realista:
- Añadir amortiguadores: Los sistemas reales siempre tienen disipación de energía
- Consideración de las no linealidades: Los muelles no siempre siguen Ley de Hooke4 perfectamente
- Contabilización de las vibraciones forzadas: Las fuerzas externas modifican el comportamiento del sistema
- Incluidos los efectos de acoplamiento: El movimiento en una dirección puede afectar a otras direcciones
Optimización de la relación de amortiguación: ¿Qué experimentos dan mejores resultados?
La amortiguación es la mejor defensa contra los problemas de resonancia. Encontrar la relación de amortiguación óptima a través de la experimentación puede mejorar drásticamente el rendimiento y la fiabilidad del sistema.
Coeficiente de amortiguación5 Los experimentos de optimización consisten en probar sistemáticamente distintas configuraciones de amortiguación para encontrar el equilibrio ideal entre el control de las vibraciones y la capacidad de respuesta del sistema. La relación de amortiguación óptima suele situarse entre 0,2 y 0,7, lo que proporciona una supresión de las vibraciones suficiente sin una pérdida excesiva de energía.
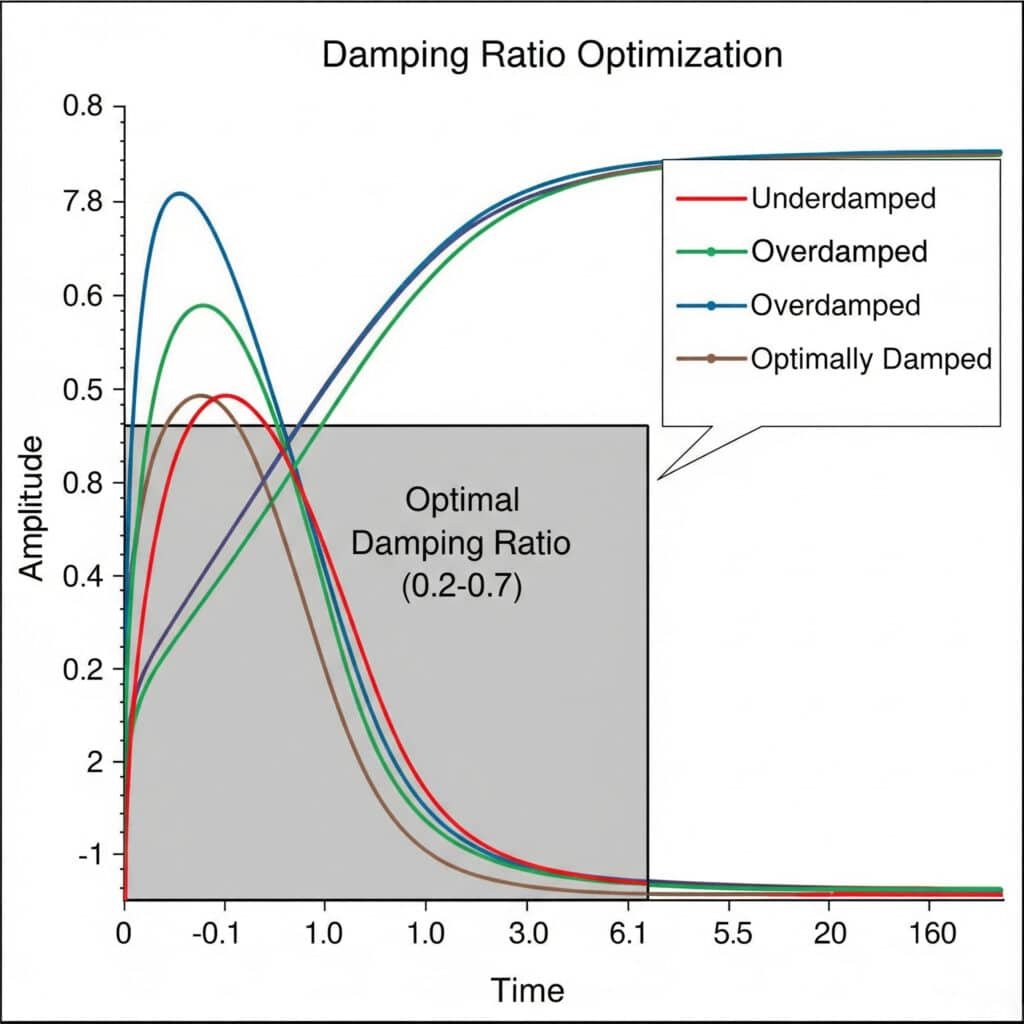
El mes pasado, ayudé a un fabricante francés de equipos de procesamiento de alimentos a resolver los persistentes problemas de vibración de sus cilindros magnéticos sin vástago. Mediante una serie de experimentos con la relación de amortiguación, descubrimos que su diseño original tenía una relación de amortiguación de solo 0,05, demasiado baja para evitar problemas de resonancia.
Montaje experimental para la prueba del coeficiente de amortiguación
Realizar experimentos de optimización de la amortiguación efectiva:
- Medición de referencia: Registra la respuesta del sistema sin amortiguación adicional
- Pruebas incrementales: Añade elementos de amortiguación en incrementos controlados
- Medición de la respuesta: Mide la amplitud, el tiempo de estabilización y la respuesta en frecuencia
- Análisis de datos: Calcular la relación de amortiguación para cada configuración
- Validación: Verificar el rendimiento en condiciones reales de funcionamiento
Comparación de tecnologías de amortiguación
| Tecnología de amortiguación | Ventajas | Limitaciones | Aplicaciones típicas |
|---|---|---|---|
| Amortiguadores viscosos | Rendimiento predecible, temperatura estable | Requieren mantenimiento, posibles fugas | Maquinaria pesada, equipos de precisión |
| Amortiguadores de fricción | Diseño sencillo y rentable | Desgaste con el tiempo, comportamiento no lineal | Soportes estructurales, maquinaria básica |
| Amortiguación del material | Sin piezas móviles, compacto | Rango de ajuste limitado | Instrumentos de precisión, aislamiento de vibraciones |
| Amortiguación activa | Adaptable a las condiciones cambiantes | Complejo, requiere energía | Aplicaciones críticas, equipos de velocidad variable |
Optimización de la amortiguación para distintas condiciones de funcionamiento
La relación de amortiguación ideal no es universal: depende de su aplicación específica:
- Operaciones de alta velocidad: Las relaciones de amortiguación más bajas (0,1-0,3) mantienen la capacidad de respuesta
- Aplicaciones de precisión: Las relaciones de amortiguación más altas (0,5-0,7) proporcionan estabilidad
- Sistemas de carga variable: Puede ser necesaria una amortiguación adaptativa
- Entornos sensibles a la temperatura: Considerar materiales amortiguadores con propiedades estables
Caso práctico: Optimización de la amortiguación de cilindros sin vástago
Al optimizar un cilindro sin vástago de doble efecto para una máquina de envasado, probamos cinco configuraciones de amortiguación diferentes:
- Cojines estándar: Coeficiente de amortiguación = 0,12
- Cojines extensibles: Coeficiente de amortiguación = 0,25
- Amortiguadores externos: Coeficiente de amortiguación = 0,41
- Soportes de montaje compuestos: Coeficiente de amortiguación = 0,38
- Enfoque combinado (3+4): Coeficiente de amortiguación = 0,53
El enfoque combinado proporcionó el mejor rendimiento, reduciendo la amplitud de las vibraciones en 78% y manteniendo unos tiempos de respuesta aceptables.
Conclusión
Comprender la resonancia de las vibraciones mediante el cálculo de la frecuencia natural, el modelado masa-resorte y la optimización de la relación de amortiguación es crucial para evitar averías en los equipos. La aplicación de estos principios permite prolongar la vida útil de la maquinaria, reducir los tiempos de inactividad y mejorar el rendimiento general del sistema.
Preguntas frecuentes sobre la resonancia vibratoria
¿Qué es la resonancia de las vibraciones en los equipos industriales?
La resonancia de las vibraciones se produce cuando una fuerza externa coincide con la frecuencia natural de un sistema, provocando oscilaciones amplificadas. En los equipos industriales, este fenómeno puede provocar movimientos excesivos, fatiga de los componentes y fallos catastróficos si no se gestiona adecuadamente.
¿Cómo puedo saber si mi sistema tiene resonancia?
Busque síntomas como aumentos de ruido inexplicables, vibraciones visibles a velocidades específicas, fallos prematuros de componentes y degradación del rendimiento que se produce en puntos de funcionamiento constantes. Las herramientas de análisis de vibraciones pueden confirmar las condiciones de resonancia.
¿Cuál es la diferencia entre vibración forzada y resonancia?
La vibración forzada se produce siempre que una fuerza externa actúa sobre un sistema, mientras que la resonancia es la condición específica en la que esa frecuencia forzada coincide con la frecuencia natural del sistema, dando lugar a una respuesta amplificada. Toda resonancia implica vibración forzada, pero no toda vibración forzada provoca resonancia.
¿Cómo afecta el diseño de un cilindro neumático sin vástago a sus características de vibración?
El diseño de los cilindros neumáticos sin vástago, con su carro móvil, su sistema de sellado interno y sus mecanismos de guía, plantea problemas de vibración únicos. El perfil extendido actúa como una viga que puede flexionarse, la masa del carro crea fuerzas de inercia y las bandas de sellado pueden introducir fricción variable.
¿Qué modificaciones sencillas pueden reducir la resonancia en los equipos existentes?
Para los equipos existentes con problemas de resonancia, considere la posibilidad de añadir masa para cambiar la frecuencia natural, instalar amortiguadores externos o amortiguadores, modificar los métodos de montaje para incluir el aislamiento de vibraciones o ajustar las velocidades de funcionamiento para evitar las frecuencias resonantes.
-
Proporciona una explicación básica de la resonancia mecánica, a menudo con ejemplos visuales, demostrando cómo una pequeña fuerza periódica puede producir oscilaciones de gran amplitud en un sistema. ↩
-
Ofrece una visión detallada de la física de la frecuencia natural, la frecuencia específica a la que un sistema tiende a oscilar en ausencia de cualquier fuerza impulsora o amortiguadora. ↩
-
Explica los principios del modelo masa-resorte, una idealización fundamental en física e ingeniería utilizada para analizar sistemas complejos que presentan movimiento armónico simple. ↩
-
Detalla la Ley de Hooke, un principio de la física que establece que la fuerza necesaria para extender o comprimir un muelle una cierta distancia es directamente proporcional a esa distancia. ↩
-
Describe la relación de amortiguación, una medida adimensional que define cómo decaen las oscilaciones de un sistema tras una perturbación, lo que es fundamental para controlar la resonancia. ↩


