¿Tiene problemas con la velocidad lenta de los cilindros, el movimiento incoherente o la fuerza insuficiente en sus sistemas neumáticos? Estos problemas tan comunes suelen deberse a un malentendido: la resistencia al flujo. Muchos ingenieros dimensionan sus componentes neumáticos basándose únicamente en los requisitos de presión y fuerza, pasando por alto el impacto crítico de la resistencia al flujo en el rendimiento en el mundo real.
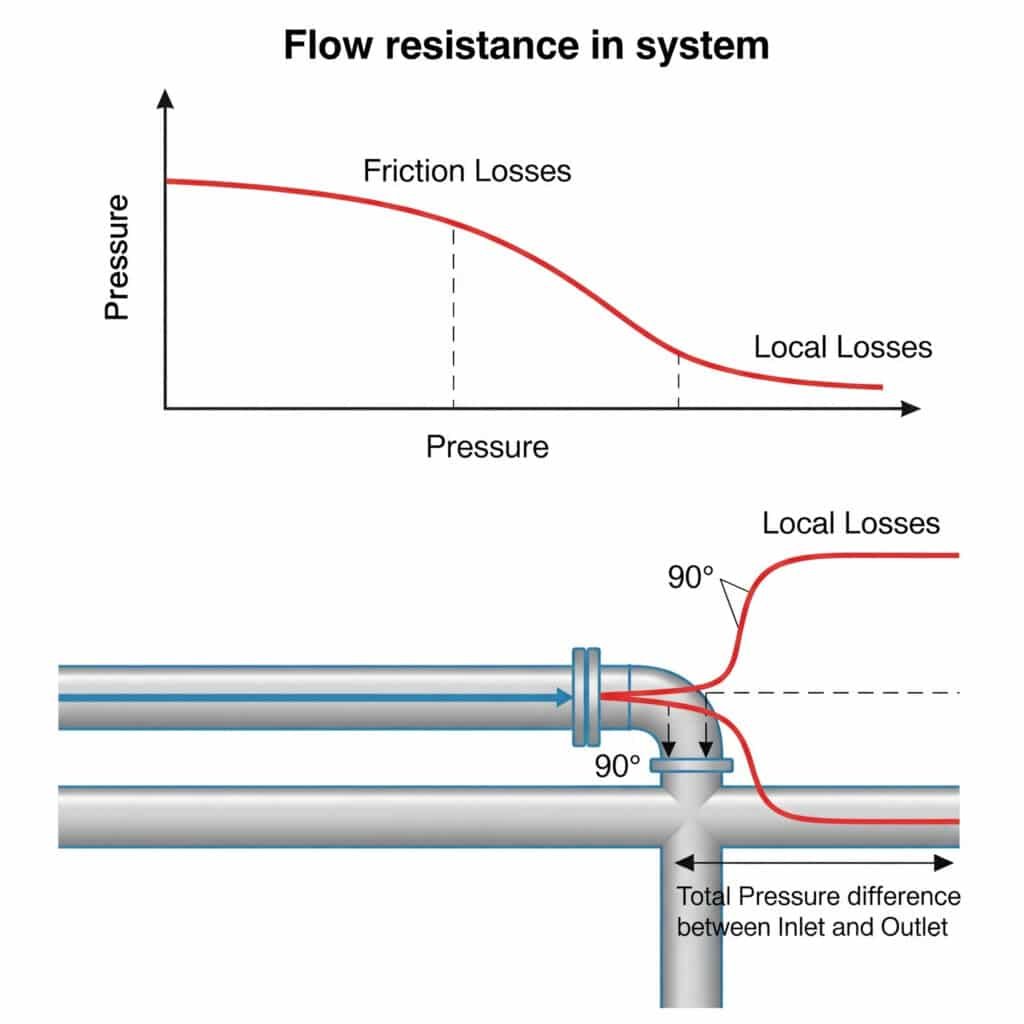
La resistencia al flujo en los sistemas neumáticos crea caídas de presión que reducen la fuerza disponible, limitan la velocidad máxima y provocan movimientos incoherentes. Esta resistencia proviene tanto de la fricción a lo largo de tuberías rectas (pérdidas por fricción) como de interrupciones en accesorios, curvas y válvulas (pérdidas locales). Juntas, estas resistencias pueden reducir el rendimiento real del sistema en 20-50% en comparación con los cálculos teóricos.
En mis más de 15 años en Bepto trabajando con sistemas neumáticos, he visto innumerables casos en los que comprender y abordar la resistencia al flujo ha transformado sistemas de bajo rendimiento en operaciones fiables y eficientes. Permítame compartir lo que he aprendido sobre cómo calcular y minimizar estos asesinos ocultos del rendimiento.
Índice
- ¿Cómo se calculan realmente las pérdidas por fricción en líneas neumáticas?
- ¿Por qué es fundamental el método de la longitud equivalente para diseñar sistemas precisos?
- ¿Qué ocurre cuando el aire fluye por secciones de diámetro reducido?
- Conclusión
- Preguntas frecuentes sobre la resistencia al flujo en sistemas neumáticos
¿Cómo se calculan realmente las pérdidas por fricción en líneas neumáticas?
Las pérdidas por fricción en tuberías y conductos rectos son la base de los cálculos de resistencia al flujo, pero muchos ingenieros se basan en reglas empíricas demasiado simplificadas que conducen a sistemas infradimensionados.
Las pérdidas por fricción en los conductos neumáticos se calculan mediante la fórmula Ecuación de Darcy-Weisbach1: ΔP = λ(L/D)(ρv²/2), donde λ es el factor de fricción, L es la longitud de la tubería, D es el diámetro de la tubería, ρ es la densidad del aire y v es la velocidad del flujo. En los sistemas neumáticos, el factor de fricción λ varía en función de Número de Reynolds2 y la rugosidad relativa, y suele determinarse utilizando tablas de consulta o el Diagrama de Moody3.
Comprender las pérdidas por fricción tiene implicaciones prácticas para el diseño de sistemas y la resolución de problemas. Permítanme desglosarlo en ideas prácticas.
Uso eficaz de las tablas de factores de fricción
El factor de fricción (λ) es el parámetro clave para calcular las caídas de presión, pero para determinar su valor hay que tener en cuenta las condiciones del flujo:
| Régimen de caudal | Número Reynolds (Re) | Determinación del factor de fricción |
|---|---|---|
| Flujo laminar | Re < 2000 | λ = 64/Re |
| Flujo de transición | 2000 < Re < 4000 | Poco fiable - evite diseñar en esta gama |
| Flujo turbulento | Re > 4000 | Utilizar tablas de consulta basadas en la rugosidad relativa (ε/D) |
Tabla de consulta práctica del factor de fricción
Para el flujo turbulento en sistemas neumáticos, utilice esta tabla simplificada:
| Material de la tubería | Rugosidad relativa (ε/D) | Factor de fricción (λ) con números de Reynolds comunes |
|---|---|---|
| Re = 10.000 | ||
| Tubo liso (PVC, poliuretano) | 0.0001 – 0.0005 | 0.031 |
| Tubos de aluminio | 0.001 – 0.002 | 0.035 |
| Acero galvanizado | 0.003 – 0.005 | 0.042 |
| Acero oxidado | 0.01 – 0.05 | 0.054 |
Cálculo de la pérdida de carga en sistemas neumáticos reales
Veamos un ejemplo práctico:
| Parámetro | Valor/Cálculo | Ejemplo |
|---|---|---|
| Diámetro del tubo (D) | Diámetro interior | 8 mm (0,008 m) |
| Longitud del tubo (L) | Longitud total recta | 5m |
| Caudal (Q) | A partir de los requisitos del sistema | 20 litros/segundo estándar |
| Densidad del aire (ρ) | A presión de funcionamiento | 7,2 kg/m³ a 6 bar |
| Velocidad del flujo (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Número Reynolds (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Rugosidad relativa | Para tubos de poliuretano | 0.0003 |
| Factor de fricción (λ) | De la tabla de consulta | 0.017 |
| Pérdida de carga (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Aplicación en el mundo real: Solución de problemas de velocidad de los cilindros
El año pasado trabajé con Sarah, una ingeniera de fabricación de una empresa de equipos de envasado de Wisconsin. Su sistema de cilindros sin vástago funcionaba a solo 60% de la velocidad prevista, a pesar de tener el cilindro del tamaño correcto y la presión de suministro adecuada.
Tras analizar su sistema, descubrí que utilizaba tubos de 6 mm para una aplicación de gran caudal. Las pérdidas por fricción provocaban una caída de presión de 2,1 bares, lo que reducía considerablemente la fuerza y la velocidad disponibles. Al cambiar a tubos de 10 mm, redujimos la caída de presión a 0,4 bares, y su sistema alcanzó inmediatamente el rendimiento requerido sin ningún otro cambio.
Factores que afectan a las pérdidas por fricción en sistemas reales
Varios factores influyen en las pérdidas reales por fricción:
- Temperatura del aire: Las temperaturas más altas aumentan la viscosidad y la fricción
- Contaminación: La suciedad y el aceite pueden aumentar la rugosidad efectiva
- Doblado de tubos: La microdeformación de los tubos doblados aumenta la resistencia
- Deterioro por la edad: La corrosión y los depósitos aumentan la rugosidad con el tiempo
- Presión de funcionamiento: Las presiones más altas aumentan la densidad y las pérdidas
¿Por qué es fundamental el método de la longitud equivalente para diseñar sistemas precisos?
Las pérdidas locales en accesorios, válvulas y codos suelen superar las pérdidas por fricción en tuberías rectas, pero muchos ingenieros las ignoran o utilizan métodos de estimación rudimentarios que provocan problemas de rendimiento.
El método de la longitud equivalente convierte las pérdidas locales de accesorios y válvulas en una longitud equivalente de tubería recta que causaría la misma pérdida de carga. Esto se calcula utilizando Le = K(D/λ), donde Le es la longitud equivalente, K es la coeficiente de pérdida local4D es el diámetro de la tubería y λ es el factor de fricción. Este método simplifica los cálculos y proporciona predicciones más precisas del rendimiento del sistema.
Veamos cómo aplicar eficazmente este método al diseño de sistemas neumáticos.
Tablas de longitudes equivalentes para componentes neumáticos comunes
He aquí una práctica tabla de referencia para los componentes neumáticos más comunes:
| Componente | Valor K | Longitud equivalente (Le/D) |
|---|---|---|
| Codo de 90° (afilado) | 0.9 | 30 |
| Codo de 90° (radio estándar) | 0.3 | 10 |
| Codo de 45 | 0.2 | 7 |
| Unión en T (flujo pasante) | 0.3 | 10 |
| Unión en T (flujo derivado) | 1.0 | 33 |
| Válvula de bola (totalmente abierta) | 0.1 | 3 |
| Válvula de compuerta (totalmente abierta) | 0.2 | 7 |
| Acoplamiento rápido | 0.4-0.8 | 13-27 |
| Válvula de retención | 1.5-2.5 | 50-83 |
| Válvula reguladora de caudal estándar | 1.0-3.0 | 33-100 |
Aplicación del método de la longitud equivalente
Para utilizar este método con eficacia:
- Identifique todos los componentes de su circuito neumático
- Hallar el valor K o la relación de longitud equivalente (Le/D) para cada componente.
- Calcule la longitud equivalente multiplicando por el diámetro del tubo
- Sume todas las longitudes equivalentes a la longitud real del tubo recto
- Utilice la longitud efectiva total en sus cálculos de pérdida por fricción
Por ejemplo, un sistema con 5 m de tubo recto de 8 mm más cuatro codos de 90°, una unión en T y dos enchufes rápidos:
| Componente | Cantidad | Le/D | Longitud equivalente |
|---|---|---|---|
| Codos de 90 | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| Unión en T | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Enchufes rápidos | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Longitud equivalente total | 0.72m | ||
| Longitud recta real | 5.00m | ||
| Longitud efectiva total | 5.72m |
Esto significa que tu sistema de 5 m se comporta en realidad como un sistema de 5,72 m debido a las pérdidas locales: un aumento de 14,4% en la longitud efectiva.
Caso práctico: Optimización de la colocación de válvulas en sistemas de montaje
Hace poco ayudé a Miguel, un ingeniero de automatización de una planta de montaje de componentes electrónicos de Arizona. Su sistema de pick-and-place experimentaba variaciones incoherentes de movimiento y tiempo de ciclo, a pesar de utilizar componentes de alta calidad.
El análisis reveló que el colector de válvulas estaba situado a 3 m de los cilindros y que el circuito incluía numerosos accesorios. El cálculo de la longitud equivalente mostró que su distancia real de 3 m tenía una longitud efectiva de 7,2 m debido a las pérdidas locales, ¡más del doble de la distancia de la tubería recta!
Al reubicar el colector de válvulas más cerca de los cilindros y eliminar varios racores, redujimos la longitud efectiva de 7,2 a 2,1 metros. Esto redujo la caída de presión en 70%, lo que se tradujo en un movimiento uniforme y una reducción de 15% en el tiempo de ciclo.
Consejos prácticos para minimizar las pérdidas locales
Para reducir las pérdidas locales en sus sistemas neumáticos:
- Utilizar codos redondeados en lugar de curvas cerradas (reduce el valor K en 67%)
- Minimizar el número de accesorios planificando rutas más directas
- Seleccione componentes de baja restricción como válvulas de bola de paso total cuando proceda
- Dimensionar correctamente los racores - los accesorios subdimensionados provocan pérdidas desproporcionadas
- Colocar las válvulas cerca de los actuadores para minimizar la longitud efectiva de los tubos
¿Qué ocurre cuando el aire fluye por secciones de diámetro reducido?
Las secciones con orificios reducidos en los circuitos neumáticos -como válvulas parcialmente cerradas, racores de tamaño insuficiente o transiciones de diámetro- crean importantes restricciones de caudal que pueden afectar gravemente al rendimiento del sistema.
Cuando el aire circula por secciones de diámetro reducido, caídas de presión5 se producen según la fórmula ΔP = ρ(v₂² - v₁²)/2, donde v₁ es la velocidad antes de la restricción y v₂ es la velocidad en la restricción. Esto puede compensarse utilizando el factor de compensación de la relación de diámetro interior C = (1 - (d/D)⁴), donde d es el diámetro reducido y D es el diámetro original. Este factor ayuda a predecir el rendimiento real del sistema y a evitar el subdimensionamiento de los componentes.
Exploremos las implicaciones prácticas de las secciones de diámetro reducido y cómo tenerlas en cuenta en el diseño de sistemas.
Cálculo de las caídas de presión en las transiciones de diámetro
Cuando el aire pasa de un diámetro mayor a otro menor, la pérdida de carga puede calcularse mediante:
| Parámetro | Fórmula | Ejemplo |
|---|---|---|
| Diámetro original (D) | De las especificaciones | 10 mm |
| Diámetro reducido (d) | De las especificaciones | 6 mm |
| Relación de diámetro interior (d/D) | División simple | 0.6 |
| Caudal (Q) | A partir de los requisitos del sistema | 15 litros/segundo estándar |
| Velocidad en la tubería original (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Velocidad en sección reducida (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Pérdida de carga (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Factor de compensación (C) | C = (1 - (d/D)⁴) | 0.87 |
Escenarios comunes de reducción del diámetro interior y su impacto
He aquí cómo afectan las distintas reducciones de diámetro interior a la capacidad de caudal:
| Reducción de diámetro | Reducción de la capacidad de caudal | Aumento de la pérdida de carga |
|---|---|---|
| De 10 mm a 8 mm | 36% | 2.4× |
| De 10 mm a 6 mm | 64% | 7.7× |
| De 10 mm a 4 mm | 84% | 39× |
| De 8 mm a 6 mm | 44% | 3.2× |
| De 8 mm a 4 mm | 75% | 16× |
| De 6 mm a 4 mm | 56% | 5.1× |
Estas cifras ponen de manifiesto por qué reducciones de diámetro aparentemente menores pueden tener efectos dramáticos en el rendimiento del sistema.
El efecto acumulativo de múltiples restricciones
En los circuitos neumáticos reales, se producen múltiples restricciones en serie. Su efecto es acumulativo y puede calcularse mediante:
- Convierte cada restricción en su factor C equivalente
- Calcula el factor C total: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Utilice este factor total para determinar la reducción global del rendimiento del sistema
Caso práctico: Solución de problemas de desajuste entre válvulas y actuadores
El mes pasado trabajé con Thomas, supervisor de mantenimiento de una fábrica de muebles de Carolina del Norte. Su nuevo sistema de cilindros sin vástago funcionaba a menos de la mitad de la velocidad prevista, a pesar de utilizar el tamaño de válvula recomendado por el fabricante.
La investigación reveló múltiples reducciones de calibre en su circuito:
- Línea de alimentación de 10 mm a puertos de válvula de 8 mm (C₁ = 0,36)
- Conexiones de válvula de 8 mm a racores de 6 mm (C₂ = 0,44)
- Racores de 6 mm a puertos de cilindro de 8 mm con restricciones internas (C₃ = 0,32).
El factor de compensación total era Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, lo que significa que su sistema perdía 75% de su capacidad de caudal teórica.
Mediante la actualización a componentes de tamaño adecuado en todo el sistema, eliminamos estas restricciones y logramos el rendimiento requerido sin cambiar el cilindro o la presión de suministro.
Estrategias prácticas para minimizar las pérdidas por reducción de perforaciones
Para reducir las pérdidas por reducción de perforaciones:
- Dimensionar los componentes de forma coherente en todo el circuito neumático
- Utilice el tamaño de tubo más grande posible para aplicaciones de gran caudal
- Atención a las restricciones de los componentes internosno sólo el tamaño de las conexiones
- Considerar vías de flujo paralelas para grandes caudales
- Elimine adaptadores y transiciones innecesarios siempre que sea posible
El principio del "eslabón más débil" en los sistemas neumáticos
Recuerde que el rendimiento de su sistema neumático está limitado por su componente más restrictivo. Un solo elemento subdimensionado puede anular las ventajas de los componentes correctamente dimensionados del resto del sistema.
Por ejemplo, un sistema con tubos de 10 mm, válvulas de 10 mm, pero accesorios de 6 mm en el cilindro funcionará esencialmente igual que un sistema con componentes de 6 mm en todo el sistema, con un coste superior.
Conclusión
Comprender y calcular correctamente la resistencia al flujo -mediante tablas de factores de fricción, métodos de longitud equivalente y compensación de diámetro reducido- es esencial para diseñar sistemas neumáticos que funcionen como se espera en condiciones reales. Aplicando estos métodos de cálculo y principios de diseño, podrá optimizar sus aplicaciones de cilindros sin vástago y otros sistemas neumáticos para obtener el máximo rendimiento y fiabilidad.
Preguntas frecuentes sobre la resistencia al flujo en sistemas neumáticos
¿Cuánta caída de presión es aceptable en un sistema neumático?
La caída de presión aceptable depende de los requisitos de su aplicación, pero como pauta general, limite la caída de presión total a 10-15% de la presión de suministro para un funcionamiento eficaz. Para un sistema de 6 bares, esto significa mantener la caída de presión total por debajo de 0,6-0,9 bares. Las aplicaciones críticas pueden requerir caídas de presión aún menores, de 5-8%, para mantener un rendimiento constante.
¿Cuál es la relación entre el diámetro del tubo y la pérdida de carga?
La caída de presión es inversamente proporcional a la quinta potencia del diámetro (D⁵) para el flujo turbulento en sistemas neumáticos. Esto significa que duplicar el diámetro del tubo reduce la caída de presión aproximadamente 32 veces. Por ejemplo, pasar de un tubo de 6 mm a otro de 12 mm puede reducir la caída de presión de 1,5 bar a sólo 0,047 bar en las mismas condiciones de flujo.
¿Cómo puedo determinar el tamaño de tubo adecuado para mi aplicación neumática?
Seleccione el tamaño del tubo en función de los requisitos de caudal y de la caída de presión aceptable. Calcule el número de Reynolds y el factor de fricción y, a continuación, utilice la ecuación de Darcy-Weisbach para determinar la caída de presión para diferentes diámetros. Elija el diámetro más pequeño que mantenga la caída de presión dentro de los límites aceptables (normalmente <10% de la presión de suministro) teniendo en cuenta las limitaciones de espacio y el coste.
¿Qué crea más restricción: un codo de 90° o 5 metros de tubo recto?
Un codo agudo de 90° suele crear una resistencia equivalente a 30 diámetros de tubo recto. Para un tubo de 8 mm, un codo cerrado equivale aproximadamente a 240 mm (30 × 8 mm) de tubo recto. Esto significa que 5 metros de tubo recto crean unas 21 veces más restricción que un solo codo. Sin embargo, los sistemas suelen contener múltiples codos y accesorios, cuyo efecto acumulado puede superar las pérdidas por longitud recta.
¿Cómo afectan los enchufes rápidos al rendimiento del sistema?
Los enchufes rápidos estándar suelen introducir una pérdida local equivalente a 15-25 diámetros de tubería recta. Además, muchos enchufes rápidos tienen restricciones internas inferiores a su tamaño nominal. Un enchufe rápido de "10 mm" puede tener una restricción interna de sólo 7-8 mm, lo que crea una reducción del diámetro interior que puede reducir la capacidad de caudal en 50-70% en ese punto.
¿Qué impacto tienen las válvulas de control de caudal parcialmente cerradas en el rendimiento del sistema?
Una válvula reguladora de caudal cerrada a 50% de su área total de paso no reduce el caudal sólo en 50%, sino en aproximadamente 75% debido a la relación no lineal entre el diámetro y la capacidad de caudal. La caída de presión aumenta en función del cuadrado del cambio de velocidad, por lo que reducir a la mitad el diámetro efectivo aumenta la caída de presión aproximadamente 16 veces en las mismas condiciones de caudal.
-
Proporciona un desglose detallado de la ecuación de Darcy-Weisbach, una fórmula fundamental y muy utilizada en dinámica de fluidos para calcular la pérdida de presión debida a la fricción en una tubería. ↩
-
Ofrece una definición clara del número de Reynolds, una magnitud adimensional crítica utilizada para predecir patrones de flujo (laminar o turbulento) en diferentes situaciones de flujo de fluidos. ↩
-
Presenta el diagrama de Moody, un gráfico completo que traza el factor de fricción de Darcy en función del número de Reynolds y la rugosidad relativa, que es la herramienta estándar de los ingenieros para determinar la caída de presión en las tuberías. ↩
-
Explica el concepto de valor K, o coeficiente de pérdida local, un número adimensional utilizado para caracterizar la pérdida de presión en un accesorio de tubería o válvula como parte del método de longitud equivalente. ↩
-
Detalla la física que subyace a la caída de presión que se produce cuando un fluido atraviesa una restricción (un orificio), basándose en los principios de la ecuación de continuidad y el principio de Bernoulli. ↩



